鞍式支承大直径平直型钢管桥内力计算分析

沈 晔

（上海市政工程设计研究总院（集团）有限公司，上海 200092）

0 引言

随着市政公用事业的不断发展，大直径自承式钢管跨越结构得到了越来越多的应用。在管道工程敷设沿线，自承式钢管桥是管道跨越河流、池塘、软弱地基等障碍所采用的主要形式之一。

自承式钢管跨越结构的支座型式有很多，常用的基本型式可分为鞍式支座和环式支座两类。其中，鞍式支座因其施工方便的特点得到了更广泛的应用[1]。工程实践表明，对于采用鞍式支座的大直径钢管桥，往往因为支座处内力过大而选用较大的钢管壁厚，从管道结构设计方面显出一定的不合理性。本文拟通过数值试验，研究管桥的内力分布规律，为管道结构设计提供参考。

1 管壁内力计算方法

给排水管道结构的壁厚t一般均不大于1/10管内径D，属于薄壁圆筒[2]。管道结构计算时，可采用的方法有结构力学方法、弹性力学有限元方法和边界单元法[3]。现行管道设计规程推荐的方法均为结构力学方法，其主要计算思路是：确定管道结构荷载图式及管道基础反力图式[2]，然后根据力学原理或试验结果给出内力计算系数。

《自承式给水钢管跨越结构设计规程》[4]给出的鞍式支承处钢管（见图1）管壁环向最大弯矩的计算公式如下:

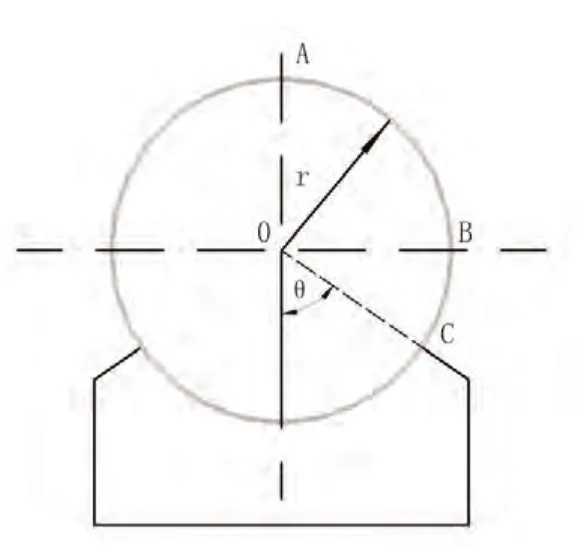
图1 鞍式支承钢管示意图

式中：Mθ——作用于鞍式支承长度上管壁的环向弯矩，N·mm；

R——支承宽度Bs上的竖向反力，N；

κ——鞍式支承处管壁的环向弯矩系数，见表1；

r——钢管内半径，mm。

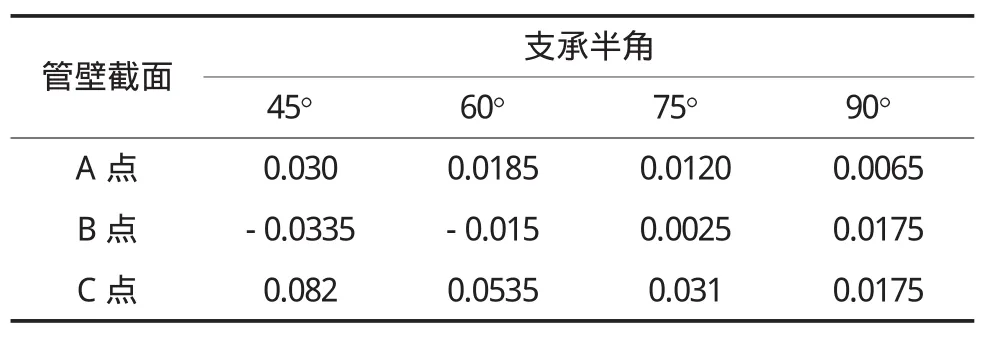
表1 鞍式支承处管壁环向弯矩系数κ一览表

采用结构力学方法计算管道结构，其特点是计算简单实用。实践表明，采用规范推荐公式和内力计算系数进行管道结构设计安全可行。然而，这种方法没有考虑管道结构与支承基础间的变形协调，不能反映管道刚度与基础支承刚度之比发生变化时的影响。

本文引入Winkler地基模型模拟管道结构与支承基础间的相互作用，应用有限元方法，对鞍式支承的平管桥进行数值计算，分析钢管桥的应力分布规律，研究鞍式支座处的应力特点，为自承式平直型钢管桥的优化设计提供参考。

Winkler地基模型假定基础单位面积上所受的压力p与基础的竖向位移y成正比，即：p=ky，式中k为基床系数[5]。根据弹性薄板计算理论，winkler地基模型下，对于承受上部荷载q和基础反力共同作用的弹性薄板，弹性曲面基本微分方程为：

ω——弹性薄板的挠度；

k——Winkler基庆系数；

D——薄板截面的弯曲刚度。

2 平管桥三维有限元数值计算

2.1 模拟对象

本文确定以支承在钢筋混凝土支墩上的较大直径的自承式平直型给水钢管桥作为研究对象。选取的实例为：两跨DN1800平管桥，钢管壁厚18 mm，两端支座及中间支座采用钢筋混凝土鞍式支墩，中心跨距16.500 m×2跨，支墩长1 500 mm。

2.2 有限元数值模型

根据研究问题的需要，建立的三维有限元网格如图2所示。模型网格划分共得到4 968个单元，4 992个节点。钢管管壁结构采用四节点矩形壳元模拟，鞍形支座对钢管结构的约束采用基于Winkler地基模型的单向弹簧施加于支座支承角范围内对应的节点上。

图2 平管桥三维有限元网格示意图

钢管管壁结构的本构关系按按各向同性线弹性考虑，其计算参数[6]：重度ρ＝78.5 kN/m3；弹性模量E＝2.06×108kPa；泊松比μ＝0.3。

计算荷载主要考虑管道自重和管内静水压力。

数值模型总体坐标系以向上为Z轴正向，沿管道纵向为X轴正向，Y轴正向根据右手准则确定。壳元局部坐标系以指向钢管截面圆心为Z轴正向，X轴正向同总体坐标X轴，Y轴正向根据右手准则确定。

2.3 管内静水压力荷载图式

当管内充满无压液体时，液体会对管壁产生静水压力。该项计算采用的管内静水压力荷载图式如图3所示[7]。

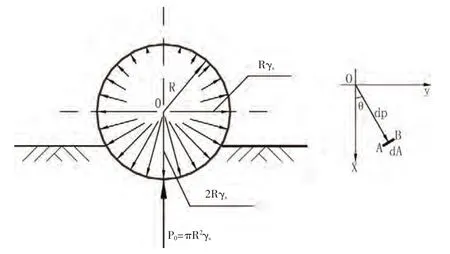
图3 管内静水压力荷载图式

坐标系原点与圆管圆心重合，Ox轴向下，θ角以逆时针旋转为正。在圆管曲面上任取条形微元面AB，微元面面积dA,微元面上的压力dP方向垂直于微元面，大小为：

2.4 Winkler基床系数

应用Winkler地基模型时，合理的选择基床系数k值对计算成果的精确性和可靠性有着重大的意义。国内外学者进行了大量的理论分析和原位试验，提出了若干个计算Winkler基床系数的经验公式，如高尔布诺夫－伯沙道夫公式、魏锡克公式、国生刚治公式等[8]。通过对各经验公式构成的研究，可以发现国生刚治公式较全面地表达了基础刚度、薄板刚度、薄板厚度等对基床系数有影响的变量因素。有文献[9]对各经验公式进行了计算比较，推荐采用国生刚治公式计算基床系数。国生刚治公式表达如下：

式中：E0为基础弹性模量；Eh为薄板弹性模量；m0为基础泊松比；m为薄板泊松比；h为薄板厚度。

本文研究对象为支承在混凝土支墩上的钢管，管壁厚为18 mm。根据国生刚治公式计算可得Winkler基床系数为7.66×108kN/m3。这个结果符合一些学者对钢与混凝土间k值的推断[10]。

3 数值计算成果及分析

3.1 钢管内力分布规律

图4、图5分别给出了支承角为120°时钢管环向弯矩Myy和纵向弯矩Mxx分布云图，根据壳元局部坐标系的定义，弯矩正负号以管内壁受拉为正，管外壁受拉为负。

图4 钢管环向弯矩M yy云图

图5 钢管纵向弯矩M xx云图

从图4图、5中可以看出，钢管弯矩在管道中部变化平稳，在两端及中间支座附近变化幅度逐渐加大。钢管弯矩的正负极值均发生在中间支座处。环向正弯矩极值为6.70 kN·m，环向负弯矩极值为-3.06 kN·m；纵向正弯矩极值为4.24 kN·m，纵向负弯矩极值为-0.97 kN·m。相比支座处，管桥跨中弯矩则小了很多。管桥跨中环向弯矩绝对极值仅为0.39 kN·m，跨中纵向弯矩绝对极值仅为0.11 kN·m。这说明，平直型管桥的支承断面为结构设计控制性断面。

3.2 鞍式支承段钢管内力

在中间支座鞍式支承范围内选取一断面，图6给出了支承角为120°时该断面的环向弯矩Myy、纵向弯矩Mxx、环向剪力Qy的分布示意图。

图6 鞍式支承处断面内力分布示意图

从图6中表达出的内力分布规律可知，鞍式支承段内力最大值发生在120°支承边界处，在支承中心处各内力值达到最小。环向弯矩Myy、纵向弯矩Mxx、环向剪力Qy极值均发生在支承边界处。环向弯矩Myy的数值约为纵向弯矩Mxx的3～4倍，环向弯矩Myy对管壁主应力的贡献更大。

在鞍式支承边界处，环向应力、纵向应力、剪应力均达到最大，是管桥结构的危险点。结构计算时需考虑此处结构在复杂应力状态下的强度条件。这与现行设计规程[4]认为的环向弯矩最大值发生点相同。

3.3 与现行规程推荐计算方法的比较

以前述数值分析模拟的原型实例为对象，本文依据现行规范[4]推荐的计算方法和公式进行了计算，并将计算结果与有限元数值计算结果进行了比较。表2给出了鞍式支承处管壁环向最大弯矩的规范公式计算结果与有限元数值计算结果。从表中可以看出，两者均表达出环向最大弯矩随鞍式支承角增大而减小的规律，但数值差别较大。规范公式计算值约为数值计算值的4～5倍，倍数关系随支承角的增大而减小。这说明按现行设计规程设计大直径钢管桥时有较大的安全储备。另一方面，规范未给出对结构内力有一定贡献的纵向弯矩的计算方法。

表2 环向最大弯矩计算结果一览表

4 结论与建议

4.1 结论

（1）本文的有限元数值计算成功预测了管桥结构的内力分布。这表明，在给排水工程等特种结构领域，对于一些较难获得解析解的力学问题，可以引入数值计算技术进行分析，并与传统的经验性的解答结果对比，可为结构设计优化提供有益的参考。

（2）计算结果表明，对于自承式平直型管桥，其支承断面为结构设计的控制性断面；在鞍式支承边界处，环向应力、纵向应力、剪应力均达到最大，是管桥结构的危险点，这与现行规程设定的最大内力发生点相同。

（3）通过数值计算结果与现行设计规程计算结果的比较，可以发现两者计算表达出的规律近似，但数值差别较大。这表明按现行设计规程设计大直径钢管桥时有较大的安全储备。

4.2 建议与思考

（1）对于鞍式支承大直径平直型钢管桥，其管桥跨中弯矩相比支座处弯矩要小很多。如果在鞍式支承处给管壁结构采取合适的加固措施，可在一定程度上减小管桥结构的钢管壁厚，使设计更加合理、经济，更加节约。

（2）管道与基础间的基床系数取值对管道内力计算结果有一定影响，确定合理的基床系数对精确的计算结构内力有着重大的意义。因此，有必要对钢管结构与混凝土基础间的基床系数的取值作进行进一步的深入研究。

[1]潘家铮.压力钢管[M].北京：水利电力出版社,1982.

[2]《给水排水工程结构设计手册》编委会.给水排水工程结构设计手册[M].北京：中国建筑工业出版社，2007.

[3]黄海燕，巫友群，王德信.带有刚性基础的地下埋管应力分析方法探讨[J].水利水电科技进展，2002，22(6)：20-22.

[4]CECS 214:2006,自承式给水钢管跨越结构设计规程[S].

[5]高大钊.土力学与基础工程[M].北京：中国建筑工业出版社，1998.

[6]GB 50017-2003,钢结构设计规范[S].

[7]（苏）克利恩，T.k.著.金吾译.地下管计算[M].北京:中国工业出版社,1964.

[8]中国船舶工业总公司第九设计研究院.弹性地基梁及矩形板计算[M].北京：中国建筑工业出版社，1998.

[9]王晖，张杏丽.大型混凝土水池基床系数的确定[J].低温建筑技术，2007，(2)：81-82.

[10]朱伯芳.有限单元法及其应用[M].北京：中国水利水电出版社，1998.