斜拉桥的非线性分析及减震研究

尹 华，吴 念

（1.广东省建筑设计研究院，广东广州 510010；2.中交第二航务工程勘察设计院有限公司，湖北武汉 430000）

0 引言

目前，斜拉桥被广泛应用于中大跨度桥梁中，相应的抗震设计方法也正在从传统的强度理论向非线性抗震理论过渡。非线性抗震理论区别于强度理论，主要在于通过结构选定部位的塑性变形来抵抗地震作用。一方面，塑性变形能消耗地震能量，从而减小地震的影响[1]；另一方面，塑性铰的出现使结构的周期延长，从而减小地震所产生的惯性力[2]。

为了保证非线性抗震设计的安全性，必须对结构进行抗震能力验算。目前对于钢筋混凝土墩柱，可以用强度破坏准则验算抗剪强度，而用非线性破坏准则验算弯曲非线性能力。

减震装置可以用不同的材料、不同的耗能减震机制和不同的构造。桥梁的减震装置通常是由隔离器和阻尼器组成，置于梁体与墩台之间。隔离器的作用是对桥梁结构提供柔性支承，调整被隔离桥梁结构的固有周期，使其避开地震能量集中的范围，减小地震引起的地震力。本文选择的液压阻尼器，通过调整阻尼器刚度系数得到最佳减震参数。

1 工程概况及非线性时程分析方法

1.1 工程概况

吉林兰旗松花江大桥为双塔双索面预应力混凝土斜拉桥，跨径布置为102.5 m+240 m+102.5 m，见图1。索的横向间距1.1 m，塔、墩固结，主梁支承半飘浮体系，桥塔柱截面采用矩形空心断面，横桥向标准尺寸4.0 m，纵桥向标准尺寸7.0 m，拉索锚固处塔壁厚1.35 m，拉索锚固区塔内净空3.8 m×2.0 m。主塔下部采用实体断面2.95 m(横向)×7 m(纵向)。桥面以上塔高69.9l m，塔上索距2.1～2.4 m，横向索距1.0 m。主墩墩身采用箱形薄壁结构，墩中设置横隔板与塔柱连续。墩宽纵向为7.2 m，横向17.0 m，墩高13.98 m，壁厚分别为1.2 m及1.0m，采用40号混凝土。设计地震烈度为7度，按8度设防。

图1 吉林兰旗松花江大桥（单位：cm）

1.2 非线性时程分析方法

本文采用分析软件MIDAS对斜拉桥进行动力分析。分析模型中桥面系采用脊梁模式模拟[3]，拉索用桁架单元模拟，主塔采用空间梁单元模拟。地震反应分析采用时程分析方法，地震波选用El Centro地震波。

在地震作用下，斜拉桥易于损坏的部位为桥塔受力最大或相对薄弱的位置，完全延性或有限延性抗震设计是将桥墩或塔的某些部位（通常是桥墩或塔底部）设计的具有足够的延性，通过在结构选定部位的塑性变形来抵抗地震作用。本桥塑性铰设置在塔底。

《公路桥梁抗震设计细则》(JTG/TB202-01-2008)[4]对截面的等效屈服曲率定义如图2所示，将曲线等效成理想弹塑性的双线性模型，初始弹性段定义为原点与受拉钢筋首次屈服点的连线，等效屈服曲率通过调整塑性段水平线的位置使两块阴影部分的面积相等确定，等效屈服点为(φy,My)，计算中应考虑最不利轴力组合。

图2 等效屈服率定义

塑性铰长度Lp可按照《公路桥梁抗震设计细则》规定取值，即取下列两式计算结果的较小值。

式中：L为水平地震惯性力作用位置的高度；h为截面的高度；fy、ds分别为纵向钢筋的屈服强度和纵向钢筋直径。

在计算分析中，塑性铰的力学模型是在塑性铰长度的中间设置一个弹塑性回转弹簧单元来模拟。模拟塑性铰的回转弹簧刚度根据塑性铰变形等同条件得到，回转弹簧上下Lp/2的长度内采用刚性构件模拟。塑性铰的模拟见图3。

图3 塑性铰计算模型

2 动力弹塑性分析

根据抗震设防的原则，E2地震作用下允许结构出现塑性，发生损伤；即在E2地震作用下，桥梁已经进入非线性工作范围，因此只有进行结构非线性时程地震反应分析才能比较真实地模拟结构的实际反应。本文利用Midas/Civil纤维单元做动力弹塑性分析，利用纤维材料的应力—应变关系和截面应变分布形状假定较为准确的截面弯矩—曲率关系，并且考虑轴力引起的中和轴变化的影响。

根据规范要求，当设防烈度为8度时，罕遇地震E2最大地震波加速度可以取到0.3 g，重要系数为1.7，因此地震波加速度峰值取0.51 g。经计算，在罕遇地震(E2地震)纵向激励作用下，本桥梁端顺桥向位移最大值为0.352 m，塔顶顺桥向位移最大值为0.428 m，索塔塔底塑性铰处顺桥向弯矩最大值为4.55×108N·m，塑性铰转角最大值为0.0 028 rad。此时，顺桥向梁端位移、塔顶位移、塑性铰弯矩和塑性铰转角的地震时程反应如图4～图7所示，墩底塑性铰的滞回曲线如图8所示。

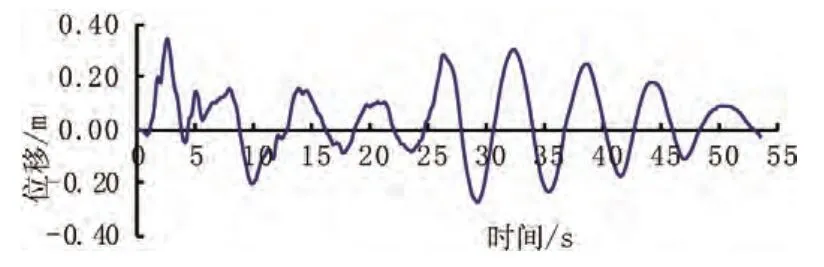
图4 纵向激励下梁端顺桥向位移反应时程

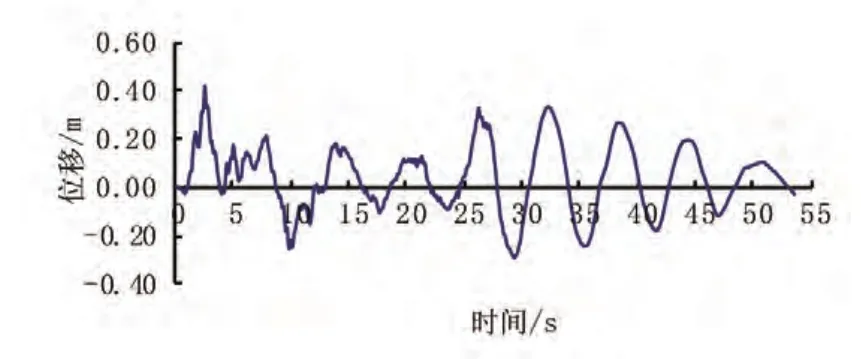
图5 纵向激励下塔顶顺桥向位移反应时程

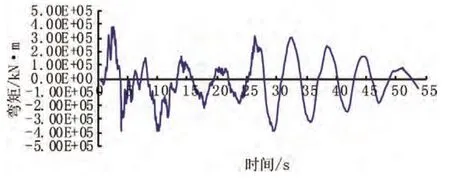
图6 纵向激励下塔底塑性铰顺桥向弯矩反应时程

图7 纵向激励下塔底塑性铰顺桥向转角反应时程

图8 塔底塑性铰处滞回曲线

3 液压阻尼器减震

3.1 液压阻尼器减震特性及力学模拟

在罕遇地震作用下，桥梁各构件的强度都满足要求，不会发生脆性破坏。但此时梁端位移都达到35 cm以上，由此可能发生落梁及支座被剪坏等次生危害。因此需在塔梁连接处进行减震设计。本桥通过设置液压阻尼器来实现构件的耗能、减震。

常用的液压阻尼器按力学特性可分为线性粘滞阻尼器和非线性粘滞阻尼器，其关系表达式为：F=Cva，式中F为阻尼力，C为阻尼系数，v为阻尼器相对速度，α为速度指数（其值在0.1～2.0之间，工程中常用的一般在0.3～1.0之间）[5]。计算模型中液压阻尼器的各项参数通过Midas/Civil软件中Maxwell的参数来模拟。在该模型中，阻尼单元与“弹簧单元”串联，简化模型如图9所示。

图9 Maxwell模型图

3.2 液压阻尼器在松花江大桥上的应用及影响

松花江大桥在纵向E2罕遇地震作用下主塔进入延性阶段，梁端和塔顶位移过大，导致梁端伸缩缝和主塔等构件受损。为保护松花江大桥各构件的安全，在塔梁交接处设置液压阻尼器，每塔梁交接处设置两个液压阻尼器，全桥共四个。建立耗能减震分析模型时，采用粘弹性耗能器对液压阻尼器进行模拟，输入罕遇地震纵向地震波，采用不同的消能器阻尼和阻尼指数分别计算。

根据之前研究可以得知：（1）当阻尼器的阻尼指数一定时，随着消能器阻尼的增大，梁端和塔顶位移和塔底弯矩基本单调减小；（2）当消能器阻尼一定时，梁端和塔顶位移和塔底弯矩随着阻尼指数的增加而减小；在工程中阻尼指数的取值范围大都在0.3～1.0之间，阻尼器的速度指数取0.3、0.4、0.5、0.6、0.7、1.0共 6个值，消能器阻尼依次取1.0×107、1.5×107、2.0×107、2.5×107共 4个值，总共组成24组参数，即24个工况进行比较，通过比选，本文取速度指数为0.7，计算4组在罕遇地震作用下的地震反应，结果比较见表1。

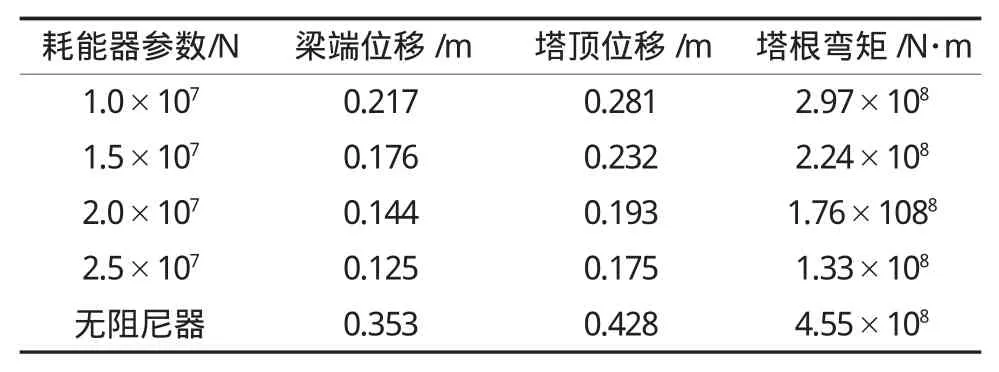
表1 耗能器参数选取对纵向地震影响

4 结论

数值计算表明，在罕遇地震（E2地震）作用下，主塔将会部分屈服进入弹塑性工作状态，具有足够的延性，抗弯能力和抗剪能力均满足要求，即主塔是安全的。主塔不会发生脆性破坏。

吉林兰旗斜拉桥安装液压阻尼器后，在罕遇地震E2作用下，地震效应明显降低，主梁梁端的纵向位移和主塔的纵向位移可以得到很好地控制，并能显著地降低塔根的弯矩，起到很好的减震和保护桥梁结构的作用。

[1]范立础，王志强.桥梁减隔震设计[M].北京:人民交通出版社,2001.

[2]范立础，卓卫东.桥梁延性抗震设计[M].北京:人民交通出版社,2001.

[3]范立础.桥梁抗震[M].上海:同济大学出版社,1997.

[4]JTJ/T B02-01-2008，公路桥梁抗震设计细则[S].

[5]叶爱君,胡世德,范立础.超大跨度斜拉桥的地震位移控制[J].土木工程学报，2004（12）:38～44.