有效抑制数学思维定式的负迁移

江苏泰州市高港实验小学（225300） 李红光

有效抑制数学思维定式的负迁移

江苏泰州市高港实验小学（225300） 李红光

在数学教学中，学生在学习过程中形成的思维定式，会给新知学习带来负迁移，干扰思考的进程，为数学概念的学习制造困境。因此，要从教学实践入手，有效抑制小学数学学习中思维定式带来的负迁移，培养学生思维的灵活性。

抑制 思维定式 负迁移

一、掌握元认知，构建认知结构

在小学数学教学中，概念、公式、定理是学生必须牢牢掌握的元认知。通过积累正确的元认知，进入新知学习时就能够举一反三、触类旁通，产生正面的积极效应。因此，教师在进行概念、公式的探究过程中，应当加强对概念本质特性的引导，帮助学生领会知识的整体性，构建良好的认知结构。例如，在教学“分数的意义”后，为了防止学生产生“分数就是表示几分之几”的思维定式，我特意设计了这样一道习题：一段绳长6米，切断2/3米后，再平分8小节，每小节是多长？每小节占总绳长的几分之几？学生容易犯错的地方有两处：一是将“切断2/3米”理解为切断绳子的2/3；二是在平分8小节后，每小节占总绳长的几分之几时，学生出现了概念混淆，认为绳长是6米，平分8小节，那么每小节就占总绳长的6/8（即3/4）。出现这两个错误的根本原因在于，学生对分数的本质没有建构良好的认知结构。为此，我进行引导：题目中的2/3是表示什么？你怎么理解这个分数？学生由此发现，题目中的2/3米是一个长度，并不代表切掉绳子的2/3。学生再审视题目，认为题目中要求出平分后每小节的长度，就要先算出平分时的绳子总长，学生列出算式（6－2/3）×1/8，得到每小节绳长为2/3米。此时我启发学生思考：现在得到的这个2/3是什么？要求出每小节占总绳长的几分之几，应当怎么算？学生认为，现在得到的2/3是平分后每段绳子的长度，可以与总绳长6米进行比对，学生由此找到问题解决的关键环节，在重新分析已知条件的基础上，使问题获得最终解决，得到每小节绳长占总绳长的几分之几。

以上教学，教师通过对数学概念本质属性的强化，引导学生重新审视分数的意义，逐步突破思维误区，从中发现自己的思维定式，展开探究，克服思维定式，从而有效抑制了思维定式造成的负迁移，提升了思维的灵活性。

二、运用对比，明确知识核心

在小学数学学习中，小学生由于年龄的原因，常常不能透过事物的表面认清本质，在碰到一些表面形式上的外部表征，往往受限于感性思维而不能做出正确的判断，因而在定式思维的推动下产生了负迁移。教学中，教师运用对比的方法，能够帮助学生辨别异同，明确数学的本质核心，抑制思维定式的负作用。

例如，在小学学过的面积公式都由多个元素构成。圆面积是半径的平方乘π，正方形的面积是边长的平方，长方形的面积是长乘宽。在学完各类面积公式之后，学生通过强化记忆，会形成一个思维定式，认为要求圆面积必须知道先知道半径，要求正方形面积必须要先知道边长，为此养成了按部就班按照公式计算的习惯，遇到特殊情况就会束手无策。教学中，在学习完圆面积和正方形面积之后，笔者补充题目展开对比教学：（1）如图1，正方形的面积是10平方厘米，求圆的面积；（2）如图2，正方形面积是10平方厘米，求圆的面积。通过题目（1）学生认识到虽然根据已知条件没法算出圆的面积，但可以通过正方形的面积公式求出正方形的边长，从而得到圆的半径。也就是说，可以通过借力，从正方形这里找到要求圆面积所需要的条件。题目（2）让学生认识到虽然不能直接算出半径，但根据正方形这一条件，可以得到圆的半径是正方形边长的二分之一，由此可以推理得到，半径的平方是正方形边长的平方的四分之一，由此题目很快就能够得到解答。

通过对比教学，学生对面积的本质有了深刻理解，提升了灵活运用面积公式的能力，大大提升了数学思维。

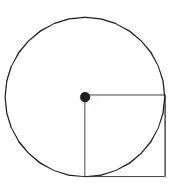
图1

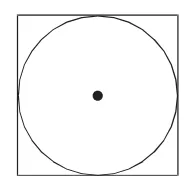
图2

三、借助变式，拓展思维广度

在数学教学中，教师讲授时往往会列举一些案例，但学生通常会将其当做唯一情形，为此，教师要尽可能引入多种变式，改变学生思维定式形成的僵化状态，拓展思维的广度，提高灵活性。

例如，在教学“两条直线垂直”这一内容时，为了让学生深刻理解“相交成直角的两条直线垂直”这一本质，我特意出示一组图形（如图3），展开变式引导。图中的五种图形，从形状上看各不相同，但实质上两条直线都是垂直的，但在初学垂直时，学生往往会认为只有第一种才是垂直的，通过对比，学生对垂直的本质属性有了深刻的认知。

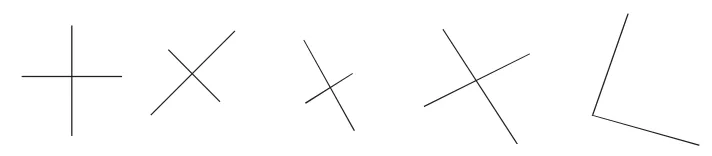
图3

总之，在小学数学教学中，数学思维定式影响学生的新知建构，教师要强化学生的元认知，加强对比，借助变式等教学方法的引导，有效抑制数学思维定式造成的负迁移。

（责编 罗 艳）

G623.5

A

1007-9068（2015）23-061