不同风嘴形式的大跨度分体箱梁桥梁颤振性能

杨泳听，周 锐，李 渊，葛耀君

（同济大学土木工程防灾国家重点实验室，上海200092）

不同风嘴形式的大跨度分体箱梁桥梁颤振性能

杨泳听，周 锐，李 渊，葛耀君

（同济大学土木工程防灾国家重点实验室，上海200092）

分体箱梁可以有效地改善整体式钢箱梁断面的气动稳定性能，但不同的风嘴类型对分体箱梁的颤振稳定性能改善程度不同。通过节段模型风洞试验对两种风嘴形式的分体箱梁的颤振性能随槽宽演化规律进行了研究，将其与Larsen，Sato和作者前期的研究结果进行了对比，并从结构动力特性参数和气动外形两个关键方面解释了研究结果差异的原因。结果表明，不对称风嘴形式分体箱梁的颤振稳定性能对槽宽比的变化比较敏感，存在一个“最优槽宽比”；对称风嘴形式分体箱梁对槽宽比的变化相对不太敏感，特别是当槽宽比较大时。与Larsen研究结果的差异主要是由结构及动力特性参数的改变造成的，其中质量惯矩的增大和扭弯比的减小起到了重要作用；与Sato研究所得结论的差异则主要源于气动外形的不同，特别是高宽比的改变。

桥梁；分体箱梁；颤振性能；风嘴形式；动力特性参数

引 言

随着桥梁设计和施工水平的不断提高，现代桥梁的跨度记录不断被刷新，如2012年建成的俄罗斯Russky Island Bridge斜拉桥达到了1 104 m而悬索桥跨度纪录更是接近2 000 m，进入21世纪后，世界桥梁工程逐步进入跨海联岛工程建设的新时期，桥梁跨度将进一步增大，预计将突破2 000 m甚至超过3 000 m。桥梁跨度大幅度增长带来的主要问题是结构刚度的急剧下降，这就使得风致振动对桥梁安全性的影响更加突出。桥梁结构的风致振动问题，尤其是桥梁颤振问题，已成为大跨度桥梁设计的主要控制因素之一［1］。

作为“第三代钢梁”的分体箱梁是继闭口箱梁之后又一次重要的大跨度桥梁主梁断面的革新，其主要优点是改善了空气动力性能，特别是提高了颤振临界风速。对于开槽箱梁的性能探索和工程应用正受到世界各国桥梁工程界的普遍关注［2］。目前，中国已建成了包括浙江西喉门大桥、上海长江大桥、香港昂船洲大桥等是采用分体箱梁主梁的大跨度缆索承重桥梁。现有的理论和试验研究［3-11］均表明在箱形主梁的中央开槽可有效地提高结构的颤振稳定性能。丹麦学者Larsen［3-4］在直布罗陀海峡大桥可行性研究中指出分体箱梁断面的颤振临界风速随槽宽增加而持续上升，并可拟合成指数律表达式；日本学者Sato［5-6］通过节段模型风洞试验研究了开槽位置和槽宽对分体箱梁结构颤振性能的影响规律，其结论是在断面中央开槽效果最好，且随着槽宽的增加结构颤振临界风速保持增长趋势，此后他又通过一座构想中的2 800 m主跨悬索桥的全桥气弹模型风洞试验验证了分体箱梁结构在改善结构颤振稳定性能上的有效性［7］；作者［8-11］对不对称风嘴形式分体箱梁的颤振性能及机理研究的结果表明：当槽宽比不大时，结构颤振临界风速随槽宽比增加而增大；当槽宽比达到最优槽宽比时颤振临界风速达到极大值；此后如果槽宽比继续增大，结构颤振稳定性能反而下降。

以上研究结果表明，作为分体箱梁断面气动外形特征最关键的一个参数——槽宽比同结构颤振稳定性能的关系尚存在争议。该争议主要体现在颤振临界风速到底是随着槽宽比的增加而持续增大还是先增后减，以上研究除了结构动力特性参数不同之外，断面气动外形也有差异。Larsen和Sato所选断面的风嘴形式均是对称的，而作者前期研究选择的分体箱梁断面的风嘴形式则是工程应用中常见的不对称形式。因此，有理由认为风嘴形式的不同是造成上述分歧可能的重要原因之一。故作者在前期研究基础之上，综合研究不对称和对称两种风嘴形式分体箱梁颤振性能随槽宽的演化规律，并从结构动力参数和气动外形两个关键影响因素方面分析了前述研究结果存在差异的原因。

1 分体箱梁颤振性能的槽宽影响规律

分别对不对称和对称风嘴形式的分体箱梁进行了节段模型风洞试验研究，并对比了颤振临界风速Ucr及临界风速增长率β与槽宽比D/Bs（D为开槽宽度，Bs为模型实体部分宽度）的关系，其中β= （Ucr-Ucro）/Ucro，式中Ucr和Ucro分别为开槽断面和原型断面的颤振临界风速。

1.1 基本断面

两种断面模型均选用了6种槽宽比D/Bs：0%， 20%，40%，60%，80%和100%。通过调整端横梁的长度来调节槽宽比，通过调整配重大小及其位置来保证质量和质量惯矩的恒定。模型断面图和相应的结构参数分别见图1和表1所示。

试验采用弹簧悬挂二元刚体节段模型，在均匀流场中进行了+3°，0°和-3°三个风攻角的试验。采用修正的最小二乘法颤振导数识别方法，利用自由振动识别颤振导数。

1.2 不对称风嘴分体箱梁的颤振性能

不对称风嘴分体箱梁断面（AS）在三个风攻角下的颤振临界风速Ucr和临界风速增长率β与槽宽比D/Bs的关系，如图2所示。

图1 两种分体箱梁断面的模型断面图Fig.1 Section diagrams of two twin-box girder models

表1 不同槽宽比两个模型的参数Tab.1 Parameters of two models with different slot-width ratios

由图2可以发现：（1）在总体趋势上，随着槽宽比的增加，该断面的颤振临界风速先增大后减小，并且存在一个最大值；（2）相同风速下，-3°初始风攻角对应的临界风速增长率最大，0°初始风攻角次之+3°初始风攻角最小；（3）不同槽宽比断面在三个风攻角下的最低颤振临界风速所对应的初始风攻角随着槽宽比的增大，逐渐发生变化，具体而言：原型断面最低颤振临界风速发生在-3°初始风攻角下；20%～40%槽比断面，最低颤振临界风速发生在0°初始风攻角下；而60%～100%槽宽比断面，最低颤振临界风速发生在+3°初始风攻角下；（4）在0～40%槽宽比范围内，颤振临界风速随着槽宽比的增加而增加；在槽宽比达到40%左右时，颤振临界风速达到最大；在40%～100%槽宽比范围内，颤振临界风速随槽宽比增加而减小，并且减小幅度比较明显。上述现象表明，该不对称风嘴分体箱梁断面的颤振稳定性能对槽宽比的变化比较敏感。

图2 不对称风嘴断面的颤振性能Fig.2 Flutter performance of twin-box girder with asymmetric wind fairings

1.3 对称风嘴分体箱梁的颤振性能

同样地，计算了对称风嘴分体箱梁（SY）的Ucr和β随槽宽比D/Bs的关系，如图3所示。

图3 对称风嘴断面的颤振性能Fig.3 Flutter performance of twin-box girder with symmetric wind fairings

由图3可以发现：（1）+3°及-3°初始风攻角下，对称风嘴分体箱梁断面的颤振临界风速随着槽宽比的增加而先增大后减小。具体而言：+3°初始风攻角下，0～40%槽宽比范围内，颤振临界风速随着槽宽比的增加而增大，且增幅较大；40%～100%槽宽比范围内，颤振临界风速随着槽宽比的增加而减小，且降幅较小；0°初始风攻角下，0～20%槽宽比范围内，颤振临界风速随着槽宽比的增加以较大的幅度增加，20%～100%槽宽比范围内，整体而言，颤振临界风速随着槽宽比的增加而增大，但增幅十分小，几乎持平；-3°初始风攻角下，0～60%槽宽比范围内，颤振临界风速随着槽宽比的增加而增大，60% ～100%槽宽比范围内，颤振临界风速随着槽宽比的增加而减小，并且降幅也较小；（2）开槽对颤振临界风速提高的程度受初始风攻角的影响而表现出的规律性，在不同的槽宽比区间也不尽相同。具体而言，在0～20%槽宽比范围内，0°初始风攻角下的颤振临界风速增长率最高，-3°初始风攻角的最低；在20%～40%槽宽比范围内，基本以+3°初始风攻角的最高，而-3°初始风攻角的最低；40%～60%槽宽比范围内，则是0°初始风攻角的最低；随着槽宽比进一步增大，即60%～100%槽宽比范围内，三个风攻角下的颤振临界风速增长率表现出一定的规律性，-3°初始风攻角的大于+3°初始风攻角的，而后者又大于0°初始风攻角的（100%槽宽比附近除外）；（3）在0～40%槽宽比范围内，颤振临界风速随着槽宽比的增加而增大，并且增大的幅度比较大；在60%～100%槽宽比范围内，颤振临界风速随着槽宽比的增加而减小，但是减小幅度不明显；40%～80%槽宽比范围内的3个断面，颤振临界风速几乎不变。

总体而言，对称风嘴分体箱梁在槽宽比较小时，颤振临界风速能够随着槽宽比的增大而迅速得以提升，当槽宽比较大时，+3°，-3°初始风攻角下颤振临界风速随着槽宽比的增加而下降的幅度也不是特别明显，并且不存在颤振临界风速较原型断面下降的现象，而0°初始风攻角下颤振临界风速不随槽宽比的增加而减小，整体上表现出比较好的稳定性。上述现象表明，在40%槽宽比以前，该对称风嘴分体箱梁断面的颤振稳定性能对槽宽比的变化比较敏感，40%槽宽比以后，颤振稳定性能对槽宽比变化的敏感度降低。

1.4 不同风嘴形式下的颤振性能对比

常见初始风攻角范围内，最低颤振临界风速对应工况下，对比不对称风嘴形式和对称风嘴形式分体箱梁断面的颤振临界风速及临界风速增长率如图4所示。

由图4可以发现：（1）两种断面的最低颤振临界风速都较高，并且都随槽宽比的增加而先增大后减小，两种断面的颤振临界风速都在40%槽宽比达到最大。（2）0～40%槽宽比范围内，对称风嘴分体箱梁的颤振临界风速及颤振临界风速增长率低于不对称风嘴分体箱梁断面的；60%～100%槽宽比范围内，对称风嘴分体箱梁的颤振临界风速及颤振临界风速增长率高于不对称风嘴分体箱梁的。不对称风嘴分体箱梁断面在槽宽比较大时，出现了颤振稳定性能较原型断面下降的现象，而对称风嘴分体箱梁断面则没有。（3）因此，当槽宽比较小时，不对称风嘴分体箱梁断面的颤振稳定性优于对称风嘴分体箱梁的；当槽宽比较大时，前者劣于后者的。而且不对称风嘴分体箱梁断面的颤振稳定性能对槽宽比变化的敏感度高于对称风嘴分体箱梁断面的。

2 槽宽比影响规律对比分析

作者及国外学者对分体箱梁断面的颤振性能研究所采用的断面都不相同，研究结果也不尽相同，这些基本断面如图5所示，相应的参数对比如表2所示。

图4 不同风嘴形式断面的颤振性能对比Fig.4 Flutter performance comparison of girders with different wind fairings

2.1 与Larsen研究结果的对比

Larsen对图5（a）中断面的颤振稳定性能进行了研究，并得出该断面的颤振临界风速随着槽宽比的增加而增大的结论，具体研究结果如图6所示（图中，横轴为开槽宽度与模型断面实体部分的比值，竖轴为不同槽宽比断面的颤振临界风速与采用Selberg颤振风速简化计算公式所得原型断面的颤振临界风速的比值［12］）。为便于对比，将本文研究结果转换为与Larsen一致的方式进行描述和对比（均为0°初始风攻角）。

由图6和表3可以发现，当槽宽比较小时，不论是对称风嘴形式断面还是不对称风嘴形式断面，本文试验所得结论与Larsen基本保持一致。然而槽宽比进一步增大之后，3种断面的颤振性能差异较大，Larsen的模型颤振临界风速继续随着槽宽比的增加而大幅增加，本文试验所选对称风嘴形式断面的颤振临界风速随着槽宽比的增加几乎不变仅是微幅增加，而不对称风嘴形式断面的颤振临界风速则随着槽宽比的增加而先增大后减小。

表2 模型的结构参数对比Tab.2 Comparison of structural parameters of models

图5 模型断面示意图Fig.5 Diagrams of the model sections

表3 本文与Larsen研究结果差异分析Tab.3 Disparity analysis of flutter performance between this paper and Larsen

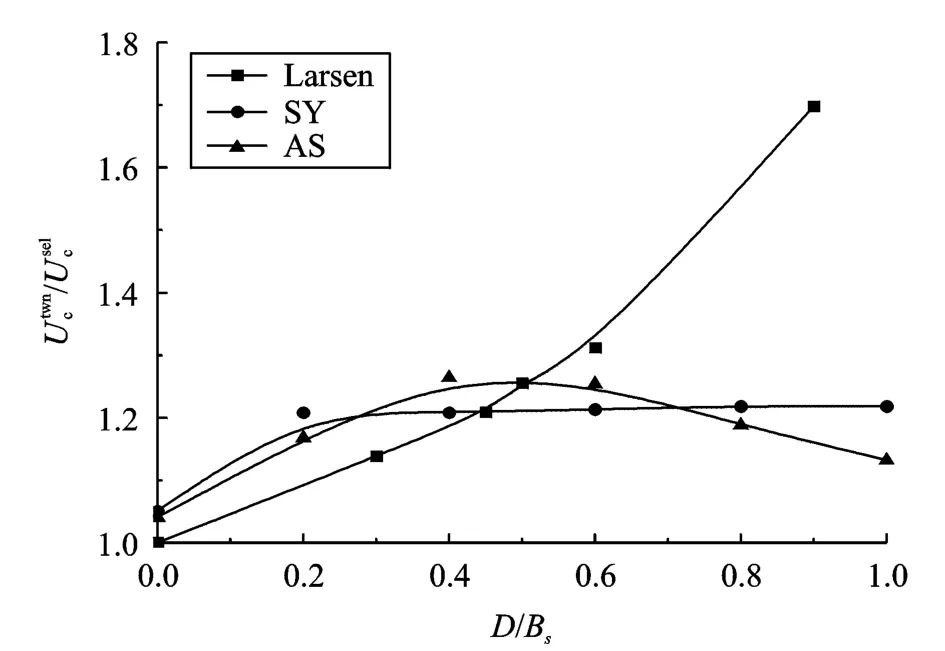
图6 本文与Larsen研究结果的对比Fig.6 Comparison of flutter performance between this paper and Larsen

2.2 与Sato研究结果的对比

Sato对图5（b）中断面的颤振稳定性能进行了研究，并得出在箱梁中央开槽能提高结构的颤振稳定性能，且提高程度随着槽宽比的增加而增加的结论，具体结果如图7所示（其中横轴为槽宽比，竖轴为不同槽宽比断面的折减颤振临界风速与原型断面的折减颤振临界风速的比值）。为便于比较，将本文研究结果转换为与Sato一致的方式进行描述和对比。

图7 本文与Sato研究结果的对比Fig.7 Comparison of flutter performance between this paper and Sato

表4 本文与Sato研究结果差异分析Tab.4 Disparity analysis of flutter performance between this paper and Larsen

由图7和表4可以发现，本文所选对称风嘴形式断面的折减颤振临界风速增长率尽管低于Sato实验所得结论，但二者在整体趋势上还是比较一致的，都是随着槽宽比的增加而增大；而不对称风嘴形式分体箱梁的折减颤振临界风速增长率依然随着槽宽比的增加先增大后减小，只是折减颤振临界风速增长率最大时，与之对应的槽宽比为60%左右（这里采用的扭转频率是发生颤振时的实测扭转频率）。

2.3 与前期研究结果的对比

作者前期研究的研究结果（最不利工况）与本文结果（最不利工况）的对比如图8所示。以本文所选分体箱梁断面的颤振临界风速增长率随槽宽变化曲线为基础，得到相应差异分析如表5所示。

图8 本文与前期研究的结果对比Fig.8 Comparison of flutter performance between this paper and the previous study

表5 本文与前期研究结果的差异分析Tab.5 Disparity analysis of flutter performance between this paper and the previous study

由图8和表5可以发现，当风嘴断面不对称时，本文研究结果与前期研究的在整体趋势上一致性较好，颤振临界风速增长率均是随着槽宽比的增加而先增大后减小。当风嘴断面对称时，本文研究所得结论与前期研究的存在一定的差异，当槽宽比较小时，对称风嘴形式断面的颤振临界风速随着槽宽比的增加而增加，当槽宽比较大时，其颤振临界风速随着槽宽比的增大而微幅下降，而前期研究研究所得结果下降幅度较大。因此，风嘴形式对分体箱梁的颤振稳定性影响的确值得重视。

3 影响因素分析

分别从结构及动力特性参数和气动外形两方面出发，对上述研究结果差异的原因进行了具体分析。

3.1 结构及动力特性参数的影响

对于不对称风嘴分体箱梁面，从总体规律上看，本文研究结果与前期研究结果比较接近，颤振临界风速都是随着槽宽比增加而先增后减，存在一个最优开槽宽度，不同之处体现在颤振临界风速的增减幅度上，前期研究所选断面的较大，其原因和二者的扭弯频率比比较接近有关。

针对对称风嘴形式断面颤振性能出现的较大分歧，以本文所选模型的结构及动力参数为基础，结合Larsen及Sato模型参数，每次仅改变一个参数，保持其他参数不变，并在相邻参数中间插值，基于二维三自由度耦合颤振分析（2d3DOF）［12］计算颤振临界风速，然后利用Sleberg颤振临界风速简化计算公式［13］来探讨结构及力特性各参数对断面颤振性能的影响。5种重要参数所对应工况编号如表6所示（其中，本文模型参数对应下标为1，Sato的下标为3，Larsen的下标为5，其他下标为对应插值所得）。

表6 5种重要参数对应编号Tab.6 Number of five important parameters

对于原型断面，由Selberg公式获得不同工况下的颤振临界风速相对于对称风嘴原型断面（对应Bs1宽度）的颤振临界风速增长率随各参数变化情况如图9所示。

图9 颤振临界风速增长率随参数变化情况Fig.9 The growths of flutter critical wind speed with five parameters

由图9可以发现，在保持其他参数不变的前提下，断面的颤振临界风速随着质量的增加而增大，随着质量惯矩的增加而增大。竖弯频率或扭转频率对颤振稳定性的的影响无法分开考虑，由图9（e）可知，当扭弯比接近1时，断面的颤振性能最差，当扭弯比远离1的时候，颤振性能逐渐好转。

对Larsen及Sato所用模型断面相关的参数进行进一步分析，得到表7，由于单独考虑竖弯或扭转频率的影响意义不大，故该表中不考虑这二者。由表7可以发现，对于Sato所选断面而言，质量惯矩的影响最大，扭弯比的影响相对较小；对于Larsen所选断面而言，依然是质量惯矩的影响最大，扭弯比的影响达到-50%左右，也不容忽视。因此，质量惯矩的影响需要重点关注，同时不能忽视扭弯比的作用。

表7 结构及动力特性参数对颤振性能影响Tab.7 Influence of structural and dynamic characteristic parameters on flutter performance

因此，从结构及动力特性参数的角度看，质量惯矩大幅增加以及扭弯比的减小导致开槽断面颤振临界风速相对于原型断面的增加幅度增大，并且在一定程度上促进了颤振临界风速随着槽宽比的增加而增大，是造成Larsen断面颤振临界风速随着槽宽比的增加而增大的幅度大于本文所选断面的重要原因；同时，Sato断面颤振临界风速高于本文结论的原因中，质量惯矩的增大带来的影响高于扭弯比的减小。

3.2 气动外形的影响

然后，保证所有断面的结构及动力特性参数与本文所选相应断面的一致，考虑模型的气动外形对颤振临界风速的影响，即：将他人所选模型的结构及动力特性参数赋给本文所选断面，然后结合本文通过风洞试验获得的气动导数，采用2d3DOF方法［12］求解各断面的颤振临界风速，得到相应的颤振临界风速增长率曲线，最后将该曲线与他人已有研究结果进行对比。和Larsen及前期研究的结论对比时，直接采用颤振临界风速增长率，此处η=（Ucr-Ucro）/Ucro×100，与Sato的结论对比时，采用折减颤振临界风速的增长率，对应的

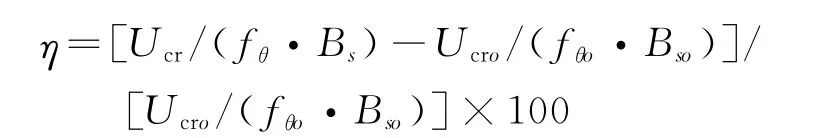
式中 Ucr，fθ及Bs分别为不同槽宽比下的振临界风速、扭转频率和模型实体宽度（Sato所用断面的Bs一直在变化，而本文所用断面的保持不变）；Ucro，fθo及Bso则为原型断面的颤振临界风速、扭转频率和模型实体宽度。相关对比结果如图10所示。

由图10可以发现，对于不对称风嘴形式断面，本文所选断面的颤振临界风速增长率随槽宽比的整体变化规律与前期研究的相似。前期研究所选断面的高宽比（接近1/8）与本文所选断面的（1/14）相差较大，但是其风嘴角度（50°）和本文的相同，由此可见风嘴角度对不对称风嘴分体箱梁断面颤振性能随槽宽的整体演化规律的影响程度大于高宽比的影响。

对于对称风嘴形式断面，整体而言本文研究结果与Larsen的比较接近，颤振临界风速都是随着槽宽比的增加而不断增大，只是20%槽宽比以后，本文所选断面的颤振临界风速增长率稍微小于Larsen的。因为Larsen所用模型的宽度远大于本文所选断面，但其高宽比接近1/14，这与本文所用的比较接近，且其风嘴角度（53°）也和本文的（50°）差异不大。因此，保证结构及动力特性参数一致时，上述气动外形的差异对最终结论的影响相对较小。

尽管颤振临界风速增长率都是随着槽宽比的增加而不断增大，Sato所用模型的折减颤振临界风速增长幅度仍然以较大的幅度高于本文所选断面的。而Sato所选模型的高宽比为1/17，较本文所用模型的1/14更小，其模型的风嘴角度（60°）较本文所用模型的（50°）更大；除此之外，Sato的模型的实体宽度随着槽宽比的增大而不断减小，导致断面的高宽比（模型高度与实体部分的宽度的比值）不断增大。故总体而言，两种模型的气动外形相差较大。接下来对这一组差异相对较大的断面进行深入分析。

图10 统一结构动力参数后的β与D/Bs关系Fig.10 The relation ofβand D/Bsafter unifying the structural dynamic parameters

由于Sato所用模型的实体宽度部分一直在改变，导致模型的高宽比也在变化，为了分析这一变化对颤振性能的影响大小，首先基于本文试验所选对称风嘴形式原型断面的结构及动力特性参数，采用Selberg颤振简化计算公式，得到断面颤振性能随梁宽变化规律，如图11所示，其中横轴为梁宽，竖轴为相对于0.14 m（对应表6中的Bs1）宽度断面的颤振临界风速增长率。

图11 SY原型断面颤振性能随梁宽Bs演化规律Fig.11 The evolution law of the flutter performance of the symmetric section with Bs

由图11可以发现，断面的颤振性能随着梁宽增加而不断下降。对于Sato试验中出现的模型断面的实体宽度，相应的颤振性能变化情况如表8所示。

表8 梁宽对颤振性能的影响Tab.8 Influence of girder width on flutter performance

由表8可以发现，相对于Sato试验中宽度为0.502 m的原型断面而言，当其槽宽比接近72%时，模型实体宽度只有0.291 m，即便不开槽，颤振临界风速增长率也将提升19%左右。

仍然采用二维三自由度耦合颤振分析方法，选择本文所用对称风嘴断面的结构及动力特性参数，基于0°初始风攻角下各槽宽比断面的颤振导数，按照Sato论文中对槽宽比的定义，通过改变模型实体部分的宽度来改变槽宽比，并取模型原型断面宽度为0.502 m，以此分析模型实体部分宽度对分体箱梁颤振性能随槽宽演化规律的影响，得到图12的对比结果。

由图12中可以发现，统一对槽宽比的定义之后，两者研究结论十分接近，折减颤振临界风速都随着槽宽比的增加而大幅增加。而Sato模型中槽宽比的变化同时体现出了高宽比的改变，因此，对于对称风嘴分体箱梁断面而言，高宽比的改变对颤振性能的影响较大。

图12 改变模型实体部分的宽度Bs对分体箱梁颤振性能的影响Fig.12 Influence of changing the width Bsof the model′s entity part on the flutter performance

综上所述，对于本文和Larsen研究所得结论的差异，主要原因在于二者结构及动力特性参数方面，其中质量惯矩的增大和扭弯比的减小起到了重要作用，气动外形的影响相对较小；对于本文与Sato研究所得结论的差异，气动外形的不同，特别是高宽比的改变，是主导力量，结构及动力特性参数中的质量惯矩的影响也不小。

4 结 论

通过对两种风嘴形式的大跨度分体箱梁桥梁颤振性能对比研究，可以得到以下主要结论：

1）不对称风嘴分体箱梁断面的颤振稳定性能对槽宽比的变化比较敏感，颤振临界风速随着槽宽比的增加而先增大后减小，存在一个“最优槽宽比”；

2）在40%槽宽比以前，对称风嘴分体箱梁断面的颤振稳定性能对槽宽比的变化比较敏感，40%槽宽比以后，该断面的颤振稳定性能对槽宽比的变化敏感度降低；

3）本文与Larsen研究结果的差异主要是由结构及动力特性参数的改变造成的，其中质量惯矩的增大和扭弯比的减小起到了重要作用，气动外形的影响程度相对较小；与Sato研究所得结论的差异则主要源于气动外形的不同，特别是高宽比的改变。

［1］ 项海帆，葛耀君.悬索桥跨度的空气动力极限［J］.土木工程学报，2005，38（1）：60—70. Xiang Haifan，Ge Yaojun.On aerodynamic limit to suspension bridges［J］.China Civil Engineering Journal，2005，38（1）：60—70.

［2］ Fumoto K.Large-scale wind tunnel test of super long suspension bridge with slotted one-box girder［A］. Proceedings of the Sixth Asia-Pacific Conference on Wind Engineering APCWE VI［C］.2005.

［3］ Larsen A.Aerodynamic aspects of the final design of the 1 624 m suspension bridge across the great belt ［J］.Journal of Wind Engineering and Industrial Aerodynamics，1993，48（2）：261—285.

［4］ Larsen A，Astiz M A.Aeroelastic consideration for the Gibraltar Bridge feasibility study，in：Bridge Aerodynamics［M］.Larsen&Esdahl（eds），Balkema，Rotterdam，1998：165—173.

［5］ Sato H，Ogihara K.Aerodynamic characteristics of slotted box girders［A］.Proceedings of Bridges into 21st century［C］.1995：721—728.

［6］ Sato H，Kusuhara S.Aerodynamic characteristics of super long-span bridges with slotted box girder［J］. Journal of Wind Engineering and Industrial Aerodynamics，2000，88：297—306.

［7］ Sato H，Hirahara N.Full aeroelastic model test of a super long-span bridge with slotted box girder［J］. Journal of Wind Engineering and Industrial Aerodynamics，2002，90：2 023—2 032.

［8］ 杨泳听，葛耀君，项海帆.大跨度桥梁中央开槽颤振控制效果和机理研究［J］.土木工程学报，2006，36（7）：74—80. Yang Yongxin，Ge Yaojun，Xiang Haifan.Flutter control effect and mechanism of central-slotting for long-span bridges［J］.China Civil Engineering Journal，2006，36（7）：74—80.

［9］ 杨泳听，葛耀君，曹丰产.大跨度悬索桥中央开槽箱梁断面的颤振性能［J］.中国公路学报，2007，20（3）：35—40. Yang Yongxin，Ge Yaojun，Cao Fengchan.Flutter performance of central-slotted box girder section for long-span suspension bridges［J］.China Journal of Highway and Transport，2007，20（3）：35—40.

［10］Yang Yongxin，Ge Yaojun，Xiang Haifan.Aerodynamic flutter control for typical girder sections of longspan cable-supported bridges［J］.Journal of Wind and Structures，2009，12（3）：205—217.

［11］邹小洁.超大跨度悬索桥颤振控制措施及其机理研究［D］.上海：同济大学，2005. Zou Xiaojie.Flutter Control Measures and Mechanism of Super-Long Span Suspension Bridges［D］.Shanghai：Tongji University，2005.

［12］杨泳听.大跨度桥梁二维颤振机理及其应用研究［D］.上海：同济大学，2002. Yang Yongxin.Two-dimensional flutter mechanism and its application for long-span bridges［D］.Shanghai：Tongji University，2002.

［13］Selberg A.Aerodynamic effects on suspension bridges ［A］.Proceedings of International Symposium on Wind Effects on Buildings and Structure［C］.Teddington，UK.1963，2：462—486.

Flutter performance of long-span twin-box girder bridges with different wind fairing forms

YANG Yong-xin，ZHOU Rui，LI Yuan，GE Yao-jun
（State Key Laboratory for Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China）

Twin box girder could effectively improve the aerodynamic stability of the cross sections of integral steel box girders. However，different wind fairing forms make various contributions to the flutter stability of the twin box girder.In this study，the relation between the flutter characteristics and the slot width of the twin box girder for two fairing forms is investigated through wind tunnel tests using the section models.Then the experimental results are compared with the research results of Larsen′s，Sato′s and the former ones of the author′s.The reasons for the discrepancy among these results are analyzed from two critical aspects of the structural dynamic characteristic parameters and the aerodynamic configurations.Results show that the flutter characteristics of the twin box girder with the asymmetric wind fairing is sensitive to the slot-width ratio which is opposite to the twin box girder with the symmetric wind fairing，especially for the case of relative large slot-width ratio.The discrepancy of these study results between this paper and Larsen′s is attributed to the structural dynamic parameters，where the increase of the mass moment of inertia and the decrease of the torsion-bending moment ratio play an important role.The discrepancy between the results of this paper and Sato′s is attributed to the aerodynamic configurations，especially the change of depth-width ratio.

bridges；twin-box girder；flutter performance；fairing form；dynamic characteristic parameters

U442.5+4；U448.25

：A

1004-4523（2015）05-0673-10

10.16385/j.cnki.issn.1004-4523.2015.05.001

杨泳听（1974—），男，副研究员。电话：（021）65988639；E-mail：yang-y-x@tongji.edu.cn

周锐（1988—），男，博士研究生。E-mail：zhourui-88@163.com

2014-04-23

2014-07-09

科技部国家重点基础研究计划（973计划）（2013CB036300）；国家自然科学基金资助项目（51078276，91015013）；交通行业重点实验室自主课题（KLWRBMT-04）；国家重点实验室自主课题（SLDRCE10-B-05）