一种新的子结构边界约束模型修正方法及其应用

李世龙，马立元，李永军，崔心瀚

（军械工程学院导弹工程系，河北 石家庄050003）

一种新的子结构边界约束模型修正方法及其应用

李世龙，马立元，李永军，崔心瀚

（军械工程学院导弹工程系，河北 石家庄050003）

子结构的边界约束状态不仅反映了其与整体结构的连接关系，而且与整体结构中该连接部位的健康状况紧密相关。为有效识别子结构的边界约束状态，基于交叉模型交叉模态（CMCM）理论，提出一种新的子结构边界约束模型修正方法。以某导弹发射台的局部子结构为对象，建立了子结构的边界约束模型，通过对边界约束刚度矩阵和质量矩阵进行修正，实现子结构边界约束状态的识别。同时，针对实测模态的不完备性以及测量噪声等问题，研究了联合基于摄动力的不完备模态扩充和截断广义奇异值技术（TGSVD）的CMCM 病态方程组求解方法。最后，通过发射台局部子结构的数值仿真算例及试验分析，验证了所提方法的有效性。

子结构；模型修正；交叉模型交叉模态；边界约束；模态扩充

引 言

模型修正是结构损伤识别的重要内容之一，作为结构动力学的反问题，它是根据试验实测信息修正初始有限元模型，使计算模态与实测模态相一致，为结构动力特性分析、损伤识别等提供初始的基准有限元模型［1-2］。然而随着结构的大型化、复杂化，由于参加修正的构建数目众多且包含误差较大，而实际测试条件往往有限，因此想从整体上对结构进行准确的模型修正非常困难［3］。对于大型复杂结构，如果能够直接对其关键部位的损伤状况进行识别，则不仅能解决整体模型修正难的问题，而且可以大大提高识别效率。

子结构法是进行结构局部动力特性分析的一种有效方法，可以只利用有限的局部实测动力信息，实现结构关键部位的模型修正及损伤识别，在工程领域具有重 要 的 应用价值［4］。Park 等［5］对 结 构 的 整体柔度进行了分解，通过子结构部位柔度的变化识别出了损伤所在位置。雷鹰等［6］将大型结构划分为多个子结构，将相邻子结构的作用视为对该子结构的“附加未知激励”，然后采用扩展卡尔曼估计和最小二乘估计识别该未知外部激励，实现了子结构的完全独立，最后将该方法应用于一个平面桁架桥的局部损伤 诊断。Wang等［7-8］对 半刚 性连 接的 边界条件辨识及模型修正进行了深入研究，并提出一种交叉模态应变能法，对一个4层钢框架结构的多种复杂边界条件进行了成功辨识。侯吉林等［9］提出一种约束子结构模型修正法，通过在子结构边界施加虚拟数值支座将子结构从整体结构中独立出来，利用子结构的局部模态构造柔度矩阵并修正该子结构，最后通过一个平面桁架结构的数值仿真验证了其有效性。

现有子结构方法将子结构从整体结构中独立出来后，单独对其进行模型修正或损伤识别，以降低计算规模，提高求解效率。然而对于大型复杂结构，各子结构的连接部位不仅是模型误差的主要来源，也是实际工作中损伤或其他故障的多发点。将子结构从整体结构中独立出来进行分析时，必须考虑其与结构其余部分的连接状态。连接部位未出现损伤时子结构的边界约束状态是一定的，一旦连接部位发生损伤后，其边界约束状态也随之改变。因此，子结构的边界约束状态不仅反映了其与整体结构的连接关系，而且与整体结构中该连接部位的健康状况密切相关。对子结构的边界约束状态进行识别，不仅能够实现局部子结构的模型修正，而且可以有效识别出子结构连接部位的损伤。为有效识别子结构的边界约束状态，基于交叉模型交叉模态理论，提出了一种新的子结构边界约束模型修正方法。以某导弹发射台的局部子结构为对象，建立了子结构的边界约束模型，通过对边界约束刚度矩阵和质量矩阵进行修正，实现子结构边界约束状态的识别。

1 子结构边界约束模型的建立

某导弹发射台为钢管焊接结构，图1中目标子结构在长期工作载荷以及发射时冲击载荷的影响下，焊接节点可能开裂，严重影响导弹的安全性和可靠性。

图1 发射台目标子结构Fig.1 Objective substructure of the launch platform model

目标子结构两端焊接节点的应力集中非常严重，是整个发射台最容易出现损伤的部位。将目标子结构从整体结构中独立出来后，若能对其边界约束状态进行有效识别，则可进一步对其两端焊接节点的健康状况做出判断。

线性无阻尼系统的自由振动方程为

式中K和M分别为系统的刚度矩阵和质量矩阵；λi和Φi为系统的第i阶特征值及其对应的特征向量。

根据子结构的基本原理，将目标子结构从两端独立出来，则特征方程可写为如下形式：

式中 下标a和b表示两端的边界自由度；下标u表示非边界自由度。当边界自由度为理想约束时，其振型分量Φa和Φb等于0，则式（2）将退化为

上式即为理想的固定约束边界条件。但对于图1中的目标子结构，由于其两端的刚度及质量未知，若直接采用上述做法将其从整体结构中独立出来，将引起很大程度的建模误差。

本文以图1中的目标子结构为对象，对其a，b两端分别施加3个平移自由度约束和3个转动自由度约束，将其从整体结构中独立出来，建立了其三维空间梁模型，如图2所示。

图2 目标子结构的三维空间梁模型Fig.2 Three-dimensional beam model of the objective substructure

将三维空间梁L的特征方程写为如下形式：

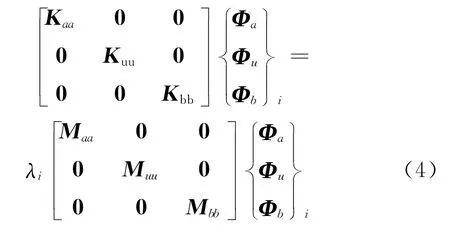
式中Kaa和Maa为 梁a端边界自由度 对 应 的 系 统刚度矩阵和质量矩 阵，Kbb和Mbb为梁b端 边界自由度对应 的 系 统刚度矩阵 和 质 量矩 阵。其 中，Kaa，Maa，Kbb和Mbb可分 解 为如 下 两部 分 ：

式中，为梁a端边界附近单元在约束自由度上的刚度分量和质量分量；，为梁b端边界附近单元在约束自由度上的刚度分量和质量分量；为梁a端约束附加刚度和附加质量；，为梁b端约束附加刚度和附加质量。

则系统的刚度矩阵可写为式中Ka和Kb为梁L的边界约束刚度矩阵，当Ka和Kb等于0时，刚度矩阵K只包含梁自身的刚度，此时梁处于理想的无约束状态；当和远大于和Kbub时，则梁处于固定约束状态；一般情况下，梁的实际的约束状态处于两者之间。

为准确模拟三维空间梁L的实际边界约束状态，本文采用6自由度的弹簧单元，包含1个轴向弹簧、2个剪切弹簧和3个转动弹簧，两端的边界单元刚度矩阵为

式 中kβ，y，ky，β和kγ，z，kz，γ为耦 合项，同 时假 定kβ，y=k y，β，kγ，z=kz，γ。

式中Ki∈R48×48为整体坐标系下的单元刚度矩阵，系统包含的单元数目为7。

在整体坐标系下，将边界单元刚度矩阵进行如下分解

式中Kn∈R48×48为整体坐标系下的边界子单元刚度矩阵。

采用Euler-Bernoulli梁的情况下，三维梁单元的刚度矩阵为

式中A为单元的横截面面积；l为单元长度；Iy为单元在xz坐标平面内的截面惯性矩；Iz为单元在xy坐标平面内的截面惯性矩；J为极惯性矩；E为拉伸弹性模量；G为剪切弹性模量。

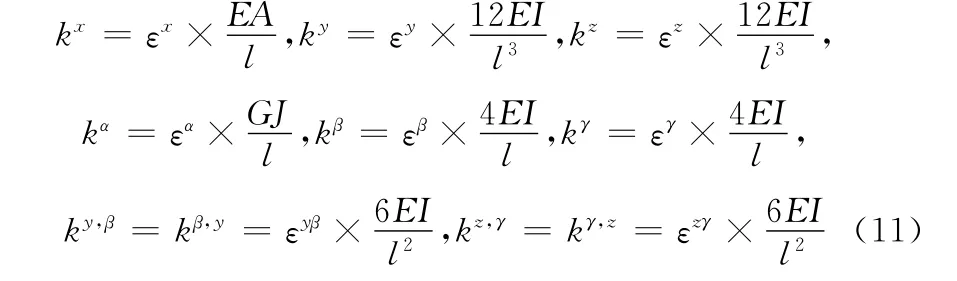
为将梁的边界约束刚度矩阵融入系统的整体刚度矩阵，采用有限元中的约束处理方法，对各边界子单元的刚度系数进行如下处理式中其中 εx，εy，εz，εα，εβ，εγ，εyβ，εzγ为 弹簧 刚 度 系数，取值为0到无穷大。当取值全为0时，表明梁两端处于无约束状态；当取值全为无穷大时，表明梁两端处于完全固定约束状态。实际结构中一般的约束状态是处于两者之间，各弹簧刚度系数的具体取值需要结合结构实际的约束条件进行确定。

对于图1中的目标子结构，由于其边界自由度含有一定动能，边界约束附加质量对结构动力特性的影响不可忽略，因此需要对其边界约束质量修正系数进行研究。采用Euler-Bernoulli梁的情况下，三维梁单元的集中质量矩阵为

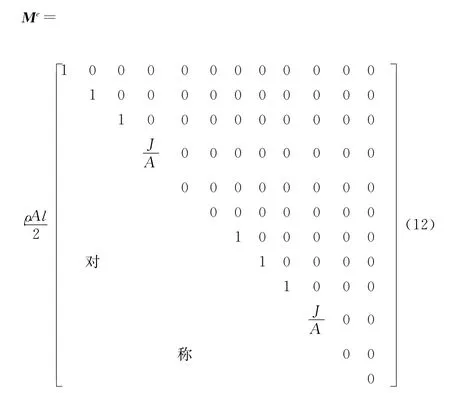
定义子结构两端的边界单元质量矩阵如下：

对边界单元的质量修正系数进行如下处理

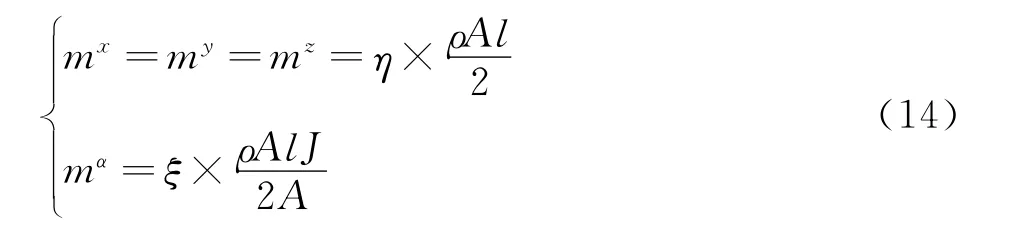
式中η为平移自由度的质量修正系数，ξ为转动自由度的质量修正系数。

在整体坐标系下，将边界单元质量矩阵作如下分解

式中Mn∈R48×48整体 坐标系 下的 边界 子单 元 质 量矩阵。

2 子结构边界约束模型修正方法

交叉 模型交叉模态法（Cross-Model Cross-Mode，CMCM）由Hu等［10］于2007年提出，兼顾了矩阵型修正法和参数型修正法的优点，不仅大大提高了修正效率，而且能够保持原模型的物理形态和修正模型的物理意义。本文采用CMCM方法，通过对边界单元刚度修正系数和质量修正系数进行调整，使系统刚度矩阵及质量矩阵发生相应改变，从而达到计算模态频率及模态振型与结构实测模态数据相匹配的目的。

2.1 CMCM 方法

假定与梁L的实测模态对应的刚度矩阵及质量矩阵分别为和，而初始有限元模型的刚度矩阵及质量矩阵分别为K和M，则可将和表示为对K和M的修正：

式中Kn和Mn分别为整体坐标系下的第n个边界子单元刚度矩阵和质量矩阵；αn和βn分别为对应的刚度修正系数和质量修正系数；NK和NM为需要修正的边界子单元刚度矩阵和质量矩阵的个数。同式（1），与实测模态对应的特征方程为

式中，^λj和为实际模态测试中得到的第j阶特征值和特征向量。对式（17）左乘（Φi）T可得：

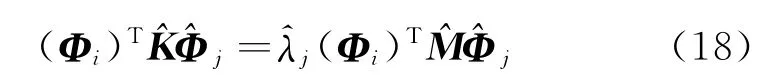
将式（16）代入式（18），则可构建子结构的CMCM 方程：

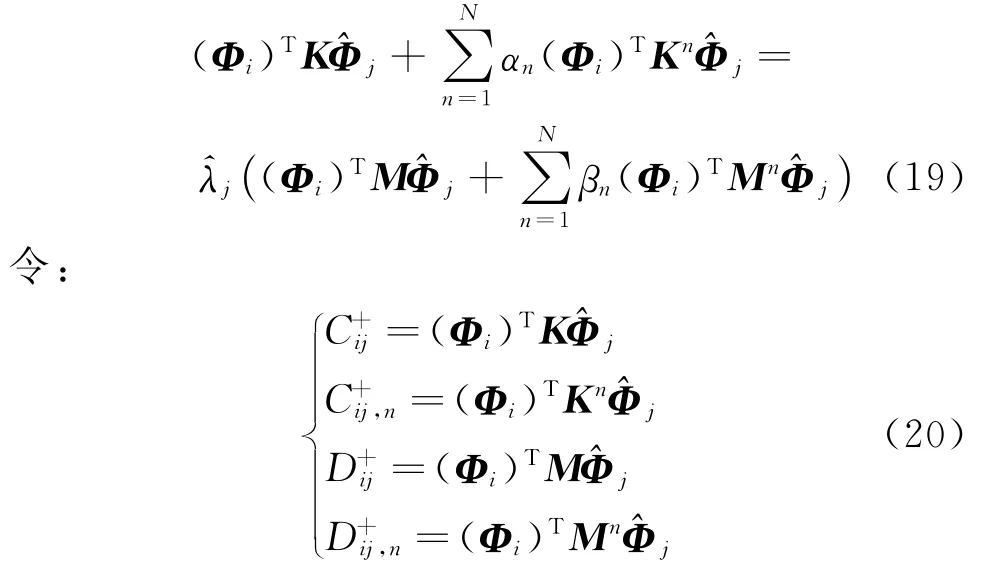
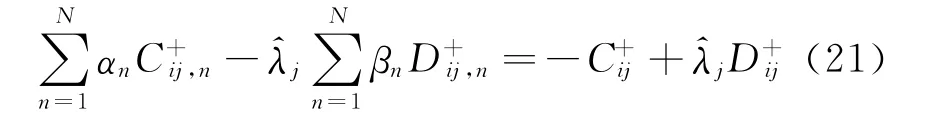
式 中C+和E+为维 数Nij×NK和Nij×NM的 矩阵；α和β为维数NK和NM的 列向 量；f+为 维数Nij的列向量。

由以上理论可以看出，CMCM 修正法可归结为对线性方程组Ax=b的求解，目前一般采用最小二乘法［11］。利用有限元分析得到的i阶模 态和 实际测试获得的j阶模态，可构建i×j个线性方程，方程数目远大于传统方法直接配对所构建的修正方程数目，因此可以利用有限阶的实测模态求解更多的修正参数。

2.2 CMCM 病态方程求解方法

CMCM 方法虽可构建多个识别方程，但该方法要求实测模态与计算模态的自由度必须一致，且对实测模态数据的精度要求非常高。然而在模态测试中，受观测自由度的限制以及测量噪声等影响，往往导致CMCM方程组Ax=b的系数矩阵A和数据项b产生扰动，从而使得方程组的解不稳定，即解的病态性。因此，实际模态测试中各种不利因素影响下的病态方程求解算法是将CMCM 子结构边界约束模型修正方法推向工程应用必须解决的问题。本文从模态扩充和正则化去噪两个方向入手，研究CMCM 病态方程的求解方法。

2.2.1 基于摄动力的不完备模态扩充

实际模态测试中，由于转动自由度及部分平移自由度不易测量，三维空间梁的实测自由度远小于有限元模型的自由度，从而导致实测振型信息空间极度不完备。

对于实测模态的不完备性，通常有两种解决思路：一种是模态扩充法，将实测模态扩充至与有限元模型自由度数目相同，使得扩充后的振型达到空间完备［12］；另一种是模型缩阶法，即对有限元模型进行缩聚，使得缩阶后的有限元计算振型与实测振型空间相一致，但该方法容易破坏原矩阵的稀疏性和对称性，导致出现虚元或负刚度［13］。

模态扩充中，若第j阶模态的已测量部分和未测量部分分别为和，则扩充后的模态为

式中T为变换矩阵，其取决于模态扩充方法。已有的模态扩充方法中，如最小二乘扩充法［14］，由于没有考虑有限元模型与试验模型之间的误差，往往导致扩充后的模态偏离较大。

为减小扩充后的模态误差，本文定义缩放系数δj如下

式中Ψj为实际测试获得的第j阶模态，Φaj为与实测模态自由度对应的初始FEM 的计算模态。则缩放后用于模态扩充的第j阶实测模态为

定义第j阶实测模态的敏感系数为

式中N为可使用的计算模态阶数，ωi为第i阶计算模态的特征值。则摄动力矢量rj为

式 中S+j=STj［SjSTj］-1为Sj的广义逆 。 根据模态扩展理论，第j阶未测模态可表示为

式中为与实测模态未测量自由度对应的第i阶计算模态中振型的“未测量”部分。因此基于摄动力的不完备模态扩充的变换矩阵可表示为

2.2.2 基于TGSVD的正则化去噪

正则化技术是应对测试噪声的一种有效方法。Tikhonov正则化技术、截断广义奇异值技术（TGSVD）和列主元QR分解技术是目前常用的3种正则化方法［15-17］。尽管目前正则化方法在理论上已经非常完善，但针对不同求解问题，同一算法的收敛性却相差很大，因此对于特定的求解问题，应选择最恰当的正则化方法。Tikhonov正则化方法通过引入正则化项来降低原不适定问题近似解的振荡性，因此往往导致近似解过度光滑，与本文子结构的实际边界刚度及质量分布相矛盾。另外，该方法一般需要结合优化算法进行迭代求解，过程较为复杂。文献［18］研究得出，当系数矩阵的奇异值呈阶梯型分布时，采用TGSVD方法求解的效果较好。对于子结构的边界约束模型修正问题，由于不同约束条件下的边界单元刚度及质量修正系数相差较大，系数矩阵的奇异值多呈阶梯型分布，故引入 TGSVD方法来减小实测模态中噪声对CMCM 方程的影响。

将病态方程组Ax=b的系数矩阵A进行奇异值分解

式中U=（u1，u2，…，un）和V=（v1，v2，…，vn）为正交特征向量，σi为矩阵A的奇异值，且满足σ1≥σ2≥…≥σn≥0。

当矩阵A为病态矩阵时，传统SVD分解存在诸多困难［19］。广义奇异值分解法（GSVD）通过引入正则化矩阵Lp×n（m≥n≥p），使病态矩阵A与L组成矩阵对 （A，L），其广 义特 征值 为矩 阵对 （^ATA，LTL）广义特征值的平方根。

方程组A x=b的正则解为

截断奇异值分解法（TSVD）通过定义截断因子

若存在σ1≥… ≥σk≥α≥σk+1≥… ≥σn≥0，则截断后的正则解为

式中k为截断数，通过直接去除小奇异值对解的贡献，达到稳定解的作用。当k=rank（A）时，该正则解相当于最小二乘解。

TGSVD方法则通过引入Ā=AL+，¯b=b-A x0分别代替TSVD方法中的矩阵A和b，其中L+为L的广义逆，本文采用L曲线法［20］选取 TGSVD 的截断数k。

3 数值仿真研究

以图1中的发射台目标子结构为对象，梁的截面为圆形，外径D=0.045 m，壁厚d=0.005 m，总长度L=0.7 m。从左至右等间隔划分为7个单元，共包含8个节点，单元的弹性模量E=2.07×1011N／m2，密度ρ=7 800 kg／m3，泊松比μ=0.27。

模型修正中，通过预设不同的边界单元刚度和质量修正系数来模拟梁的不同边界约束状态，并将该模型的计算模态数据作为“实测”模态数据，与初始有限元模型的计算模态数据联合构建CMCM 方程组。经研究发现，对于本模型，当两端的刚度修正系数达到105时，已接近完全固定约束状态。若将三维空间梁每个单元的质量视为单位质量，则试验模型除目标子结构L外的总质量为504.75，当质量修正系数取504.75，相当于将试验模型除目标子结构L外的所有质量附加在某一个边界自由度上。

梁 的初始状态视 为 两 端 简 支，即Uxa，Uya，Uza，ROTxa和Uyb，Uzb，ROTxb完 全约 束，质量 修 正系数 均为0，并将该模型作为数值仿真及试验分析的基准有限元模型。总共设置了3种边界约束工况，如表1所示。工况1中，梁a端完全约束，梁b端具有较大柔度；工况2中，梁a端的转动自由度完全约束，平移自由度及相应耦合项具有一定柔度，梁b端的平移自由度完全约束，转动自由度及相应耦合项具有一定柔度；工况3为中间状态，梁两端的平移自由度、转动自由度以及耦合项均具有一定柔度。

表1 边界约束工况Tab.1 Boundary constraint conditions

为研究方法在实际工程应用中的效果，在数值仿真中考虑了实测模态空间的不完备性以及测试噪声两个不利因素。假设在模态测试中每个节点仅测量了1个平移自由度，方向沿Y方向和Z方向交错分布，即在每个节点上只从有限元计算结果中提取这1个平移自由度的振型信息，相当于“实测”自由度数目仅为结构自由度总数目的1／6。为模拟测试噪声对修正结果的影响，在有限元计算得到的模态频率及振型中加入由Matlab标准正态分布生成的随机噪声

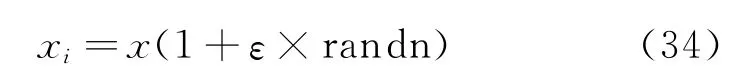
式中x为模态参数的实际计算值，xi为加入噪声后的模态参数；ε为噪声水平；randn为具有单位标准差和零均值的正态分布随机变量。本文在模态频率中加入噪声的水平为3%，在模态振型中加入噪声的水平为2%。

待修正的未知数个数为20，选取前4阶实测模态和基准有限元模型的前10阶计算模态，构建40个CMCM方程，方程数大于未知数个数，方程组有解。

在实际模态测试中各种不利因素的影响下，为研究本文方法较已有方法在求解CMCM 病态方程中的优越性，进行如下定义：

方法1：采用本文提出的CMCM 病态方程求解方法进行求解；

方法2：采用文献［11］中的改进最小二乘法对构建的CMCM方程进行求解。

分别采用以上两种方法对目标子结构的3种边界约束工况进行模型修正，各修正参数的设定值与修正值的绝对误差如图3所示。

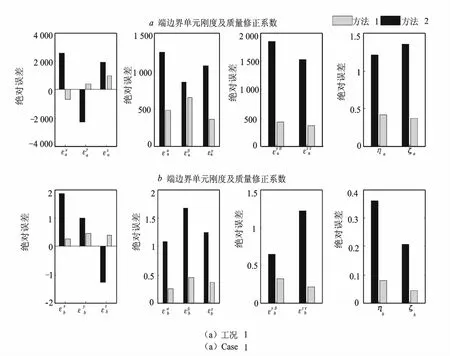
图3 模型修正结果对比Fig.3 Comparison of model updating results

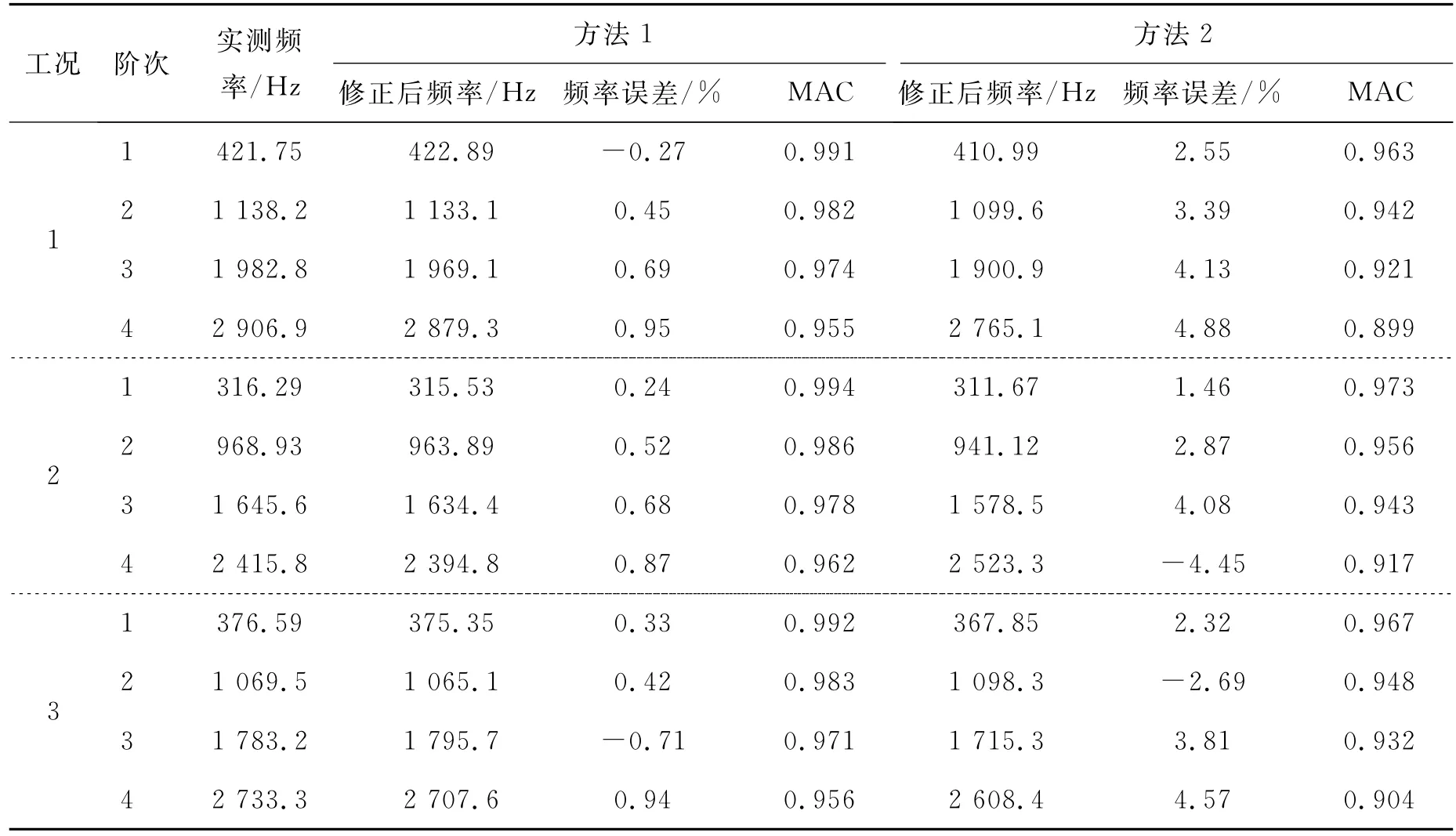
表2 修正后有限元模型动力特性对比Tab.2 Comparison of dynamic parameters of updated model

从图中可以看出，在实测模态不完备以及测试噪声等不利因素的影响下，方法1求解得出的各修正参数绝对误差非常小，能够有效识别出各个工况下子结构的边界约束状态；相比，方法2求解得出的各修正参数绝对误差过大，对目标子结构边界约束状态的识别不够准确。

两种方法修正后有限元模型的动力特性对比如表2所示。从表中可以看出，方法1修正后的计算频率与实测频率吻合较好，最大频率误差仅为0.95%，各阶振型的 MAC值也非常高；相比，受实测模态的不完备性及测量噪声影响，方法2的修正效果很不理想，最大频率误差达到了4.88%，各阶振型的MAC值也偏低。

通过对不同噪声水平下的模型修正研究发现，当频率和振型噪声水平分别为3%和2%，改进最小二乘法各修正参数的最大相对误差接近5%；当频率和振型噪声水平均为4%时，改进最小二乘法各修正参数的最大相对误差超过了10%时，且修正后频率和振型误差过大，失去修正意义。本文方法的求解精度和鲁棒性较好，当设定各修正参数的最大相对误差不超过5%时，频率和振型可添加的最大噪声水平为5%。综上，本文提出的CMCM 病态方程求解方法较改进最小二乘法具有明显优势，更适用于实际测试不利因素影响下的子结构边界约束模型修正。

4 发射台子结构边界约束模型修正

以图1中的发射台目标子结构为对象，采用本文方法对其边界约束进行模型修正，初始有限元模型仍然采用两端简支的基准模型。

4.1 模态测试

模态测试时，整个结构通过橡皮绳悬挂于试验框架上，如图4所示。

图4 模态测试现场Fig.4 The experiment scene

将目标子结构从左至右等分为7个单元，共8个节点，每个节点布置1个加速度传感器，沿Y方向和Z方向交错分布，共计8个传感器。采用锤激法进行人工脉冲激励，单点激励，多点响应。进行多次重复测试，选择测试较为稳定的数据组，以减小人为操作误差对测试数据产生的影响。采样频率为10 k Hz，每个响应信号取20 000个采样点。加速度信号经电荷放大器放大进入DH5920动态信号测试分析系统，测试分析软件采用东华模态分析软件（DHMA）。

目标子结构实测模态与初始有限元模型的计算模态对比如表3所示。

可以看出，两者误差比较大，且阶次越高误差越大，第4阶频率的误差达到了13.95%。这说明目标子结构的实际边界约束状态与初始有限元模型差别非常大，需要对其进行模型修正。

表3 目标子结构实测模态与初始有限元模型计算模态对比Tab.3 Comparison of modal parameters between nitial FEM and test results

4.2子结构边界约束模型修正

分别采用方法1和方法2，对目标子结构的边界约束进行模型修正，修正后有限元模型的计算模态与实测模态对比如表4所示。可以看出，方法1修正后有限元模型的前4阶模态频率误差显著减小，最大误差仅为0.97%，且振型的 MAC值也显著提高；相比，方法2的修正效果一般，第4阶频率误差达到了5.17%，振型的 MAC值也偏低。

方法1修正后目标子结构的边界约束刚度修正系数和质量修正系数见表5。可以看出，两端的转动自由度较平移自由度的约束更大，子结构整体处于半刚性连接状态；另外，子结构两端的质量修正系数也较大，说明边界约束附加质量对其模态特性的影响非常大。

表4 修正后有限元模型计算模态与实测模态对比Tab.4 Comparison of modal parameters between updated FEM and test results

表5 目标子结构边界约束修正系数Tab.5 Boundary constraint correction factor of the objective substructure

5 结 论

基于交叉模型交叉模态（CMCM）理论，提出一种新的子结构边界约束模型修正方法，通过对某导弹发射台局部子结构的模型修正数值仿真及试验分析，验证了所提方法的有效性，并得出以下主要结论：

（1）子结构法在大型复杂结构的动力分析中具有明显优势，通过对损伤前后子结构的边界约束状态进行识别，不仅可以实现局部子结构的模型修正，而且可进一步对子结构连接部位的健康状况做出判断。

（2）对发射台目标子结构两端分别施加6自由度的边界约束，通过构建边界单元刚度矩阵和边界单元质量矩阵，可将其从整体结构中独立出来，为子结构边界约束模型修正提供有效途径。

（3）以发射台目标子结构的实测模态参数为基准，通过对边界单元刚度修正系数和质量修正系数进行调整，可实现子结构边界约束状态的识别。

（4）实测模态的不完备性和测试噪声的影响是将CMCM子结构边界约束模型修正方法推向工程应用的主要障碍，通过提出的联合基于摄动力的不完备模态扩充和TGSVD的CMCM病态方程组求解方法能有效解决此问题。

［1］ Giuseppe Chellini，Guido De Roeck，Luca Nardinia，et al.

Damage analysis of a steel-concrete composite frame by finite element model updating［J］.Journal of Constructional Steel Research，2010，66（5）：398—411.

［2］ 李英超，张敏，李华军.利用不完备实测模态修正杆系结构约束边界条件［J］.工程力学，2013，30（1）：288—294 LI Ying-chao，ZHANG Min，LI Hua-jun.Model updating for constraint boundary conditions of member structures using incomplete measured modes［J］.Engineering Mechanics，2013，30（1）：288—294.

［3］ 侯吉林，欧进萍.联合整体和局部动态信息的空间桁架模型修正试 验［J］.振动与冲击，2013，32（16）：100—105. HOU Ji-lin ，OU Jin-ping.Model updating experiment of space truss using global and local dynamic information［J］.Journal of Vibration and Shock，2013，32（16）：100—105.

［4］ 易伟建，周云，李浩.基于贝叶斯统计推断的框架结构损伤诊断研究［J］.工程力学，2009，26（5）：121—128. Yi Wei-jian，Zhou Yun，Li Hao.Damage assessment research on frame structure based on Bayesian statistical inference ［J］.Engineering Mechanics，2009，26 （5）：121—128.

［5］ Park KC，Reich GW，Alvin KF.Damage detection using localized flexibilities［J］.Structural Health Monitoring，Current Status and Perspectives，1997：125—139.

［6］ 雷鹰，毛亦可.部分观测下基于子结构的大型结构损伤诊断法［J］.工程力学，2012，27（7）：180—185. LEI Ying，MAO Yi-ke.A damage detection algorithm based on substructures for large size structures under limited measurements ［J］.Engineering Mechanics，2012，27（7）：180—185.

［7］ Wang Shuqing，Zhang Min，Fushun Liu.Estimation of semi-rigid joints by cross modal strain energy meth-od［J］.Structural Engineering and Mechanics，2013，47（6）：757—771.

［8］ Wang Shuqing.Model updating and parameters estimation incorporating flexible joints and boundary conditions［J］.Inverse Problems in Science and Engineering，2014，22（5）：727—745.

［9］ 侯吉林，欧进萍.基于局部模态的约束子结构模型修正法［J］.力学学报，2009，41（5）：748—755. HOU Ji-lin，OU Jin-ping.Isolated substructure model updating based on local mode［J］.Chinese Journal of Theoretical and Applied Mechanics，2009，41（5）：748—755.

［10］Wang Hu S-L J，Li H，Wang S.Cross-model cross-mode method for model updating［J］.Mechanical Systems and Signal Processing，2007，21（4）：1 690—1 703.

［11］李英超.基于模态参数识别的海洋平台结构模型修正技术研究［D］.青岛：中国海洋大学，2012. LI Ying-chao.Model updating of offshore platform structures based on modal parameter identification ［D］.Qingdao：Ocean University of China，2012.

［12］刘金玉，姜建华.一种基于摄动力的不完备模态扩充方法［J］.力学季刊，2012，33（4）：590—596. Liu Jin-yu，Jiang Jian-hua.Incomplete modal expansion method using perturbed force［J］.Chinese Quarterly of Mechanics，2012，33（4）：590—596.

［13］CarvalhoJ，Dana Biswa N，Abhijit Gupta，et al.A direct method for model updating with incomplete measured data and without spurious modes［J］.Mechanical Systems and Signal Processing，2007，21（7）：2 715—2 731.

［14］BALMESE.Review and evaluation of shape expansion methods［A］.International Modal Analysis Conference［C］.San Antonio，Texas，2000：210—218.

［15］Weber B，Paultre P，Proulx J.Consistent regularization of nonlinear model updating for damage identification［J］.Mechanical Systems and Signal Processing，2009，23（6）：1 965—1 985.

［16］陈震，余岭.基于截断GSVD方法的桥梁移动荷载识别［J］. 振动与 冲 击，2014，33（10）：97—101. CHEN Zhen，YU Ling.Identification of dynamic axle loads on a bride based on truncated generalized singular value decomposition ［J］.Journal of Vibration and Shock，2014，33（10）：97—101.

［17］张纯，宋固全.去噪正则化模型修正方法在桥梁损伤识别中的应用［J］.振动工程学报，2012，25（1）：97—102. Zhang Chun，Song Gu-quan.Bridge damage identification by finite element model updating with Tikhonov regularization and wavelet denoising ［J］.Journal of Vibration Engineering，2012，25（1）：97—102.

［18］张立涛，李兆霞，费庆国，等.结构损伤识别中的若干正则化问题研究［J］.工程力学，2008，25（5）：45—52. ZHANG Li-tao，LI Zhao-xia，FEI Qing-guo，et al. Studies on some regularization problems in structural damage identification ［J］.Engineering Mechanics，2008，25（5）：45—52.

［19］Wu JR，Li QS.Structural parameter identification and damage detection for a steel structure using a two-stage finite element model updating method［J］.Journal of Constructional Steel Research，2006，62（5）：231—239.

［20］Hansen P C.Analysis of discrete ill-posed problems by means of the L-curve［J］.SIAM Review，1992，l （34）：561—580.

A method for model updating of substructure boundary constraints and its application

LI Shi-long，MA Li-yuan，LI Yong-jun，CUI Xin-han
（Department of Missile Engineering，Ordnance Engineering College，Shijiazhuang 050003，China）

The substructure’s boundary constraint condition not only reflects its relationship with the overall structure，but also reflects the close relationship with the healthy state of the connection parts.Based on cross-model cross-mode，a new method for model updating of the substructure constraints is proposed in this paper.Taking a local substructure on a certain missile launch platform as the research object，a model is established which is suited to analyze the substructure’s boundary constraint.Through updating the model with the stiffness matrix and mass matrix of boundary constraint，the boundary constraint condition of the substructure is identified.Meanwhile，aiming to overcome the shortcomings of incompleteness of measured modal data and the measurement noise，a calculation method for ill-condition CMCM equation set is proposed，which is based on incomplete modal expansion method using perturbed force and TGSVD method.Furthermore，a numerical simulation and an experiment study associated with the local substructure of the missile launch platform are conducted to examine the proposed methods.

substructure；model updating；cross-model cross-mode；boundary constraints；modal expansion

TB123；TU311；TU973.2+1

A

1004-4523（2015）05-0730-11

10.16385／j.cnki.issn.1004-4523.2015.05.007

李世龙（1987—），男，博士研究生。电话：18633482018；E-mail：li123ysu＠163.com

2014-05-19；

014-08-25