钢管柱支承单层网壳结构抗冲击动力性能试验研究

王秀丽，马肖彤，吴 长，粱亚雄，冉永红

（1.兰州理工大学土木工程学院，甘肃兰州730050；2.北方民族大学土木工程学院，宁夏银川750021；2.西部土木工程防灾减灾教育部工程研究中心，甘肃兰州730050）

钢管柱支承单层网壳结构抗冲击动力性能试验研究

王秀丽1，3，马肖彤1，2，吴 长1，3，粱亚雄1，3，冉永红1，3

（1.兰州理工大学土木工程学院，甘肃兰州730050；2.北方民族大学土木工程学院，宁夏银川750021；2.西部土木工程防灾减灾教育部工程研究中心，甘肃兰州730050）

为了研究带有下部支承柱的单层网壳结构在斜向冲击下整体结构的抗冲击动力性能，对下部支承为钢管柱的单层K6型网壳结构进行了斜向冲击试验与仿真模拟分析，得出结构的破坏模式与动力响应特性；基于大比例的钢管柱支承网壳模型冲击试验，通过动态应变仪和位移传感器、加速度传感器，获取冲击物斜向入射冲击结构时关键杆件和关键节点的时程响应数据，借助高速摄影机拍摄冲击历程、结构各阶段变形及破坏形态，并将试验研究与仿真结果进行分析对比。研究结果表明：钢管柱支承单层网壳结构在斜向冲击试验中的破坏模式可以总结为两种；斜向冲击试验所得动力响应结果与仿真分析吻合；随着冲击能量的增大，上下部结构的响应都随之增大，且下部柱大于上部网壳；随着冲击高度的提高，结构上下部的位移与应变均增大，加速度的变化情况无明显规律；动力响应由冲击部位传至整体结构的时间约为1.2～6.1 ms。

冲击试验；钢管柱；破坏模式；下部支承柱受冲击；冲击动力响应

引 言

对于网壳结构的安全性能研究一直备受人们的关注。自9.11事件以后，冲击现象也在不断地增加，冲击荷载虽然是一种偶然荷载，但是建筑结构不可避免地会遭受到外部物体的冲击、撞击以及爆炸等动力荷载的作用。如果大跨网壳结构在承受冲击荷载时一旦发生破坏或者倒塌，后果将无法估量。国内外对于框架结构在冲击荷载下的动力响应研究已比较成熟［1-5］；大跨空间结构方面：国外尚无此方面的专门研究，国内目前现有的研究仅限于李海旺，郭可等［6-7］对单层球面网壳所做的冲击荷载下的稳定性分析和试验研究；支旭东，王多智［8-9］等所做的不同形式单层网壳在冲击荷载下的破坏机理以及抗冲击防护方法研究。

已有的研究大都针对落地网壳结构，没有考虑其下部支撑结构的作用与响应；而在实际工程中，网壳均带有下部结构，且下部结构更容易受到汽车碰撞和爆炸冲击等荷载的作用，其中下部支承柱的破坏将对上部网壳以及整体结构的安全性能产生重大影响。研究带下部支撑柱的网壳结构冲击特性，对于网壳结构的应用和安全评估均有十分重要的意义。本文首次对带钢管柱支承的单层网壳试验模型考虑了当下部支承柱受到冲击作用时，下部柱自身的抗冲击动力性能以及对上部网壳受力的影响，并总结出结构的破坏模式和动力响应特性。

1 试验概况

1.1 试验模型

试验模型采用K6型单层球面网壳，跨度为3 m，矢高为0.667 m，共有90个节点，240根杆件，主肋及环杆截面尺寸为22 mm×3 mm，斜杆截面尺寸为14 mm×2 mm，采用球节点模拟集中质量，每个节点附加质量约为2.0 kg，采用D80实心球模拟节点。下部支承柱为6根高1.5 m、截面尺寸89 mm×4 mm的钢管，分别位于每个主肋相对应位置，试验模型见图1所示。

1.2 试验装置与试验方法

本次冲击试验在冲击模拟试验台上进行，试验台总高为5.83 m，坡度为42°，为了模拟不同的加载

2 数值仿真分析

工况，冲击出口高度可调节为400 mm，600 mm，800 mm，1000 mm，1 200 mm，1 300 mm不等，见图2所示。

图2 冲击模拟试验台Fig.2 Impact simulation test bench

冲击试验台由平台段和轨道段组成，冲击物（直径为100，200，300 mm的钢球）由平台或轨道中间某一部位释放，产生速度斜向冲击支承柱的不同部位。通过动态位移传感器，加速度传感器，应变片以及东华DH5922和DEWE5001动态信号测试系统采集节点和杆件的时程响应数据。在试验进行时，借助高速摄像机拍摄冲击历程、结构各阶段变形及破坏形态（应变片型号：电阻值120Ω，灵敏系数2.12，栅长栅宽5 mm×3 mm，粘贴采用半桥接法；位移传感器型号：CLMD2-AJ1A8P01XX，量程250～1 000 mm不等；加速度传感器型号：DH151XX，量程30 000g）。

本次试验旨在探讨下部支承柱的不同部位承受冲击力时整体结构的抗冲击性能，冲击能量由钢球质量与释放高度控制。试验时，冲击试验加载点分别选取一个支承柱上高度为400 mm（加载点1）、600 mm（加载点2）、800 mm（加载点3）的3个部位。各工况加载完成后间隔30 min再进行下一个工况。编排试验工况时，按照钢球释放高度相同、撞击点不同和总冲击能量相同、撞击点不同的原则，总共分为20种工况，见表1所示。

表1 试验工况Tab.1 Test conditions

1.3 测点布置

在进行试验前首先对试验模型进行各种工况作用下的仿真分析，根据仿真结果，结合试验实际情况，选择结构的关键部位进行各测点布置。

1.3.1 应变片布置

在受冲击的1号柱上贴6个应变片，相邻2号柱和对面4号柱上各贴4个应变片，在上部网壳上贴8个应变片，具体见图3所示。

1.3.2 位移测点布置

位移测点在上部网壳与1号柱相连的节点上有1个，1号柱和2号柱柱顶和柱中各2个，4号柱顶1个。

1.3.3 加速度测点布置

加速度测点布置为1号柱、2号柱和4号柱柱顶各1个，与1号柱相连的网壳节点和相邻节点各1个，网壳顶点1个。

2.1 冲击动力学微分方程

冲击荷载是短时超强荷载，在建立运动平衡方

图3 应变片布置图Fig.3 Strain gauge position

程时需利用Hamilton变分数值算法［10］。Hamilton原理可陈述如下：在两个瞬时t0和t1之间，描述物体真实运动的广义位移ξi（t）使得Hamilton作用量JH取驻值

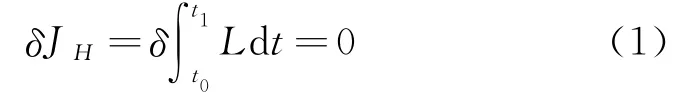
式中L为Lagrange函数，等于系统的总动能与系统的总势能之差

式中U为系统的变形能。

这是经典的Hamilton原理，适用于保守系统。但是对于非保守系统，则不能直接应用，应做如下修改，即令修正的Hamilton作用量J＇H使下式成立：式中JH，J＇H分别为Hamilton作用量与修正量；L为拉格朗日函数；为体系的总动能；V=Ku2表示体系的位能；Wnc为作用于体系上的非保守力所做的功；δ是在指定时间段内所取的变分。

公式（3）即为修正后的Hamilton原理，在同一时间间隔内，在由系统的初始位置到达最终位置的所有与真实运动相邻近的可能运动中，真实的运动使泛函J＇H取驻值。将公式（3）离散化并考虑结构阻尼的影响，得出冲击动力学微分方程为

由于冲击荷载发生的时间十分短暂，一般为亳秒级，因此，对式（5）求解时，若采用一般隐示法中的增量迭代法，需要转置刚度矩阵，但是该方法对于存在接触这样高度非线性的动力学问题很难保证计算收敛。显式方法是在每一时步内计算新的反应值，该值仅仅依赖于前一步获得的解，不需要进行平衡迭代与矩阵求逆，一般不会存在不收敛问题。因此冲击动力问题的求解通常选择显示分析方法。

2.2 仿真分析模型参数

根据冲击问题特点，选取适合于冲击分析的有限元软件ANSYS/LS-DYNA［11］进行数值模拟。分析中网壳杆件及下部柱选用三节点梁单元Beam161，屋面荷载通过质量单元Mass166以集中力的形式施加到各个节点上，冲击物选用八节点Solid164单元。考虑到在同一应变值下，动态应力要比静态应力高很多，当应变率˙ε=10-5～103s-1，应变ε=10-2时许多金属材料都的瞬时应力和屈服极限都会随着应变率的提高而提高，使得在冲击荷载作用下必须考虑材料的应变率效应。因此本文仿真分析时杆件材料选择适用于钢材而且可输入真实应力应变曲线的Cowper-Symbols率相关本构模型。采用这个材料模型，还可定义失效塑性应变。应变率与屈服应力的关系为

式中σ0为常应变率处的屈服应力；˙ε＇为有效应变率；C和P为应变率参数，低碳钢分别取40和5；fh）为基于有效塑性应变的硬化函数。

3 试验结果分析

3.1 模型工作状态与破坏模式

在冲击试验中，冲击物大小和速度不同，结构的受力和变形是不同的。当冲击物直径为100 mm时，在各种不同的释放高度下，冲击能量都非常小，冲击过后冲击物立即反弹，结构获得能量很少，结构上下部均未发生明显的变形，仍处于线性状态，见图4（a）所示；当冲击物直径为200 mm时，随着释放高度的提高，冲击能量与结构所吸收的能量均逐渐增大，受冲击柱开始出现较明显变形，结构进入初步损伤状态，由应力应变分析可知，受冲击柱逐渐进入塑性，但是由于环梁刚度较大，上部网壳基本完好，见图4（b）所示；当冲击物直径为300 mm时，受冲击柱出现非常明显的变形，与上部网壳相连接部位的焊缝发生破坏，与冲击柱相邻近部位的支承柱受力亦较大，但由于环梁刚度较大使得传递至上部网壳的能量很小，上部网壳没有出现明显的变形，整体结构经过加固修复后仍能继续使用，见图4（c）所示。由上所述，可以将冲击荷载作用下钢管柱支承单层网壳结构的破坏模式总结为两种：（1）下部柱局部变形模式；（2）下部柱与上部网壳局部变形模式。在之前所做的理论分析结果中，还会出现上部网壳大变形模式和下部柱冲切失效、上部网壳基本完好这两种破坏模式。由于后两种模式只有在冲击速度很高的情况下才能实现，而在本次试验中，试验台架使冲击速度受到限制，因此后两种破坏模式无法实现。

图4 结构各阶段变形Fig.4 Various stages deformation of structure

3.2 动态应变响应分析

杆件应变大小可以直观地反映出结构的受力分布情况。因此，首先查看在冲击荷载下关键杆件的应变变化规律。在试验模型中，将直接承受冲击荷载的部位定义为冲击区，其他支承柱和上部网壳结构定义为非冲击区。为清楚地反映结构各部分杆件应变变化和传播规律，分别选取3个位置的应变片：（1）冲击区柱；（2）非冲击区柱；（3）上部网壳关键杆件。将不同工况下应变开始响应的时刻，最大值出现时刻以及相应的应变最大值列于表2～4中。由表可见，随着冲击能量和冲击高度的增大，结构冲击区和非冲击区杆件的应变峰值均是逐渐增大。其中，随着冲击能量的增大，受冲击柱杆件应变最大增幅为4.54倍，非冲击区柱增幅最大为4.95倍，上部网壳应变增幅最大为2.73倍；随着冲击高度由400 mm到800 mm的变化，由于冲击点位置越高，下部支承柱的刚度和约束逐渐减弱，向非冲击区传递能量所需时间亦越短，非冲击区受到的冲击能量越多，从而使得整体结构冲击响应逐渐增大，3个部位杆件应变试验值增幅最大分别为1.80倍、2.05倍、1.51倍。

在结构受冲击过程中，结构杆件动态应变响应的传播具有如下规律：由于每次冲击物释放的高度与时间不同，因此各杆件应变开始响应的初始时间不同。首先，应变都是从冲击点附近开始有响应，然后通过应变率传播效应向四周传递部分冲击能量，使结构其他部位产生动力响应，即离冲击点越近的位置，其杆件应变产生响应的时刻越早且幅值也越大；离冲击点越远的位置，其杆件产生应变响应的时刻越晚且其幅值越小。其次，尽管应变响应的传播存在着先后问题，但是整个传播过程仍十分短暂。从冲击点附近杆件开始产生响应到整体结构各个部位均发生响应，耗时仅为1.2～6.1 ms左右。各杆件应变达到极值的时间为0.9 ms到27.2 ms不等，差别较为明显，但是同一杆件在不同工况时应变达到极值所经历的时间是基本相同的，由于上部网壳杆件截面比下部支承柱小，因此上部网壳的杆件应变响应大于非冲击区支承柱。

为了能够更加直观地展现应变响应的变化并验证试验结果的可靠性，分别再任意选取冲击区和非冲击区的3个关键杆件，将应变极值的试验值和仿真值绘制于图5中（1 000 mm处为柱顶，由于试验加载台的限制，冲击试验无法实现该点冲击，因此图中只绘出仿真值）。由图可见，试验值和仿真值的大小和规律都很接近，最大差距为15.4%，通过分析可知引起误差的主要原因是：仿真分析中是忽略摩擦、热能损失和冲击物变形的，而且仿真分析时无法准确地模拟出损伤累积。随着冲击点高度的增高，杆件应变值亦均随之增大。在冲击过程中，冲击区杆件逐渐进入塑性，非冲击区很少有杆件进入塑性，这是由于冲击是局部性荷载，在冲击作用下，通常是与冲击物直接接触的冲击区域承受大部分的冲击能量，然后少部分的冲击能量通过冲击区传递至非冲击区，这样就使得非冲击区和冲击区之间受力差距较大。

表2 冲击区柱的杆件应变Tab.2 Member strain of impact zone column

表3 非冲击区柱的杆件应变Tab.3 Member strain of non-impact zone column

3.3 动态位移响应分析

在冲击动力问题中，还应考虑节点动位移也就是结构变形的响应规律。由于冲击问题中持时非常短暂，选用普通的位移传感器无法测试出运动过程中位移的变化情况，因此在此次试验中采用动态位移传感器进行关键节点的位移时程曲线测试。将各种不同的工况下不同测点的位移极值大小列于表5～7中，由表可见，在不同的释放高度作用下，随着冲击能量和冲击点高度的增大，测点位移均是逐渐增大的。表中数据还可以反映出应力波的传播规律，在不同的工况中，均是测点2和测点3的位移最大，这两个测点都是位于直接承受冲击作用的支承柱上，离冲击点最近的部位，所受冲击能量较大；测点1和测点6次之，这是由于在冲击荷载作用下，结构有整体位移，因此即使测点1和测点6分别位于上部网壳和对面支承柱，位移也会随着冲击柱位移的增大而增大；由于应力波是由受冲击柱通过上部网壳传至相邻柱，因此位于相邻柱上的测点4和5位移最小，且柱顶位移大于柱中位移。

图5 应变变化Fig.5 Variation of strain

同样，由受冲击柱柱顶的位移试验值和仿真值对比变化图6可见，节点位移的试验结果和有限元仿真结果总体上都表现出相同增长趋势，最大误差为14.8%，变化规律与杆件应变变化规律相似，均是冲击点越高，节点位移值越大。因此在带下部支撑的单层网壳实际工程抗冲击设计中，适当地增强上下部结构连接处各杆件和节点的刚度以及约束强度，能够降低结构在冲击荷载作用下的变形程度，确保结构的安全性。

表5 冲击高度为400 mm时的测点位移Tab.5 Measuring point displacement when impact height is 400 mm

表6 冲击高度为600 mm时的测点位移Tab.6 Measuring point displacement when impact height is 600 mm

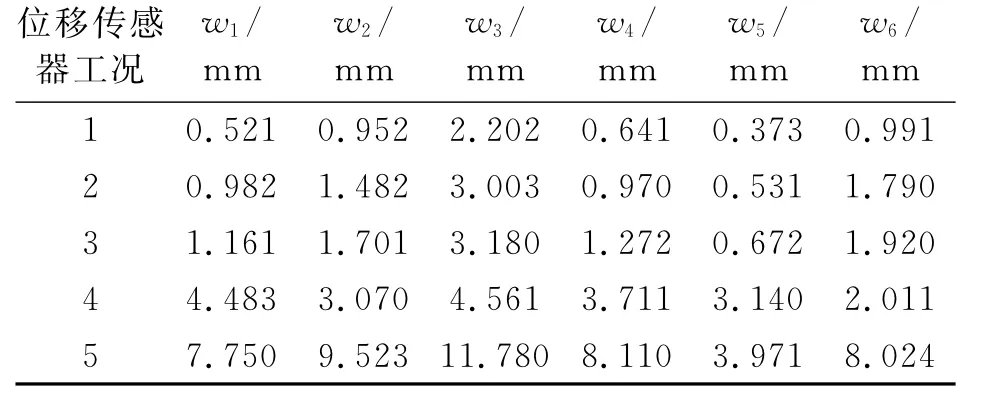
表7 冲击高度为800 mm时的测点位移Tab.7 Measuring point displacement when impact height is 800 mm

3.4 加速度响应分析

加速度响应是冲击动力问题中一个不可忽视的因素，与惯性力和结构振动状态密切相关，为了考察惯性力对结构动力响应的影响，试验中还测试了部分关键节点的加速度响应，反映结构在冲击荷载下的振动特性，如图7所示。由图可见，随着冲击能量的增大，结构加速度峰值均逐渐增大，但是随着冲击高度的变化，加速度变化情况并没有明显的规律，这是由于带下部支承的网壳结构，上下部协同工作时，结构的刚度变化和振动问题非常复杂，影响因素较多，因此其并无明显的变化规律。

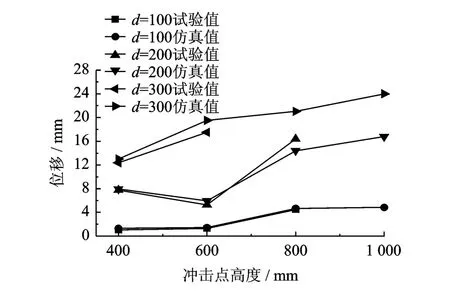
图6 位移变化Fig.6 Variation of displacement

图7 加速度变化Fig.7 Variation of acceleration

3.5 动态响应时程分析

以上所做分析都是针对某一特定的时间点，结构动力响应的变化规律，而冲击过程中的各个时间点所对应的结构响应是不同的。为了查看结构动力响应在整个冲击过程中逐渐变化的情况，选取某一工况下的任意杆件和节点，将杆件动应变，节点动位移和加速度随时间变化的响应曲线分别绘于图8中。由图可见，三项指标均是在冲击瞬间就达到峰值，随后衰减并绕着某一位置不断振动直至停止，结构的整个振动过程也极短。此外，图中还可以看出，加速度时程曲线中出现了两个极值，第1个极值也是整个加速度时程的峰值，为冲击物首次冲击引起；第2个极值为首次冲击后钢球反弹再次冲击结构或者撞击到地面引起，第2个极值明显小于首次极值。

图8 动态响应时程曲线Fig.8 Dynamic response-time history curve

4 结 论

本文通过对冲击荷载作用在单层网壳结构下部支承柱时抗冲击动力性能的模型试验研究与仿真分析，可以得到以下结论：

（1）通过对此次冲击试验所测数据进行分析并结合模型工作状态描述可以验证钢管柱支承单层网壳结构在冲击荷载作用下的两种破坏模式：1）下部柱进入塑性，上部网壳无明显变形；2）下部柱发生明显弯曲变形，上部网壳受力明显。

（2）冲击试验测试值和仿真分析值的大小和规律都很接近，验证了试验和仿真模拟结果的正确性。随着冲击物质量和速度的增大，上下部结构的动力响应（应变、位移、加速度）随之增大，由于冲击能量的传播，下部支承柱的动力响应大于上部网壳。

（3）由冲击试验得到，当冲击点位置增高时，支承柱的刚度和约束逐渐减弱，网壳的动力响应则逐渐增大。而且随着冲击位置的提高，能量由冲击区向非冲击区传递的时间越短，非冲击区受到的冲击能量越多，整体结构动力响应越大。因此，在带下部支撑的单层网壳实际工程抗冲击设计中，应尽量避免结构较高部位受到冲击作用，对于可能发生的外部冲击作用应采取一些疏导或保护措施，对于较高的潜在受冲击部位则应予以加强，适当地增强上下部结构连接处各杆件和节点的刚度以及约束强度，能够降低结构在冲击荷载作用下的变形程度，确保结构的安全性。

（4）结构从受冲击柱开始有动力响应，继而在很短的时间内向其他支承柱和上部网壳传播开来，即离冲击点越近的位置，其产生响应的时刻越早且其幅值也越大，响应由冲击部位传至整个网壳的时间约为1.2～6.1 ms。

［1］ Karagiozovaa D，Norman Jones.Dynamic buckling of elastic-plastic square tubes under axial impact［J］.International Journal of Impact Engineering，2004，30：167—192.

［2］ Nagel G M，Thambiratnam D P.Dynamic simulation and energy absorption of tapered thin-walled tubes under oblique impact loading［J］.International Journal of Impact Engineering，2006，32：1 595—1 620.

［3］ 刘锋，吕西林.冲击载荷作用下框架结构的非线性动力响应［J］.振动工程学报，2008，21（2）：107—114. Liu Feng，Lv Xilin.Nonlinear dynamic responses of impulsive loaded frame structure［J］.Journal of Vibration Engineering，2008，21（2）：107—114.

［4］ Kim H S，Kim J，An D W.Development of integrated system for progressive collapse analysis of building structures considering dynamic effects［J］.Advances in Engineering Software，2009，40：1—8.

［5］ 陆新征，江见鲸.世界贸易中心飞机撞击后倒塌过程的仿真分析［J］.土木工程学报，2001，34（6）：8—10. Lu Xinzheng，Jiang Jianjing.Dynamic finite element simulation for the collapse of World Trade Center［J］. China Civil Engineering Journal，2001，34（6）：8—10.

［6］ 李海旺，郭可，魏剑伟，等.撞击载荷作用下单层球面网壳动力响应模型实验研究［J］.爆炸与冲击，2006，26 （1）：39—45. Li Haiwang，Guo Ke，Wei Jianwei，et al.The dynamic response of a single-layer reticulated dome to drop hammer impact［J］.Explosion and Shock Waves，2006，26（1）：39—45.

［7］ 郭可.单层球面网壳在冲击荷载作用下的动力响应分析［D］.太原：太原理工大学，2004. Guo Ke.Dynamic analysis of single-layer reticulated domes under impact［D］.Taiyuan：Taiyuan University of Technology，2004.

［8］ 王多智.冲击荷载下网壳结构的失效机理研究［D］.哈尔滨：哈尔滨工业大学，2010. Wang Duozhi.Failure modes of geodesic and schwedler reticulated domes under impact loads［D］.Harbin：Harbin Institute of Technology，2010.

［9］ Zhi Xudong，Wang Duozhi，Fan Feng，et al.Mechanical behaviors of single-layer reticulated domes under impact［A］.Proceedings of the Third International Symposium on Innovative Civil&Architectural Engineering［C］.Seoul，Korea，Oct.3-4，2008：29—35.

［10］宁建国，王成，马天宝.爆炸与冲击动力学［M］.北京：国防工业出版社，2010. Ning Jianguo，Wang Cheng，Ma Tianbao.Explosion and Shock Dynamics［M］.Beijing：National Defense Industry Press，2010.

［11］安世亚太（北京）有限公司.ANSYS/LS-DYNA使用指南［M］.北京：安世亚太，1999. Pera Global（Beijing）Limited Company.ANSYS/LSDYNA Users Guide［M］.Beijing：Pera Global，1999.

［12］杜庆华，熊祝华，陶学义.应用固体力学［M］.北京：高等教育出版社，1987. Du Qinghua，Xiong Zhuhua，Tao Xueyi.Solid Mechanics［M］.Beijing：China Higher Education Press，1987.

Shock resistance dynamic performance tests on single-layer dome supported with steel tube column

WANG Xiu-li1，3，MA Xiao-tong1，2，WU Chang1，3，LIANG Ya-xiong1，3，RAN Yong-hong1，3

（1.School of Civil Engineering，Lanzhou University of Technology，Lanzhou 730050，China；2.School of Civil Engineering，Beifang University of Nationalties，Yinchuan 750021，China；3.Western Center of Disaster Mitigation in Civil Engineering of Ministry of Education，Lanzhou 730050，China）

This paper studies the shock resistance dynamic performance of single-layer dome supported with steel tube column subjected to inclined impact load.Failure modes and dynamic response characteristics are got through oblique impact test and simulation analysis on a K6 type single-layer dome supported with steel tube column.Based on the large scale reticulated dome model，strain-time history curve of key bars，displacement-time history curve and acceleration-time history curve of key nodes are collected by dynamic strain gauges，dynamic displacement sensors，and acceleration sensors under oblique incident impact action.The impact process，structural deformation and failure modes are photographed using high speed camera.The results show：the failure modes of single-layer reticulated dome supported with steel tube column can be divided into two kinds in impact test.The results of the impact test agree well with those of simulation analysis.The upper and lower structural responses are increasing with the increase of the impact energy，which of the lower column is greater than the upper dome.With the increasing of the height of the impact point height，both the upper and lower structural displacement and strain increase，and acceleration change has no obvious regularity.The dynamic transmission from the impact site to the whole dome is about 1.2～6.1 ms.

impact test；steel tube column；failure modes；the lower support column subjected to impact action；impact dynamic response

TU321+.3；TU391.3

：A

1004-4523（2015）05-0683-09

10.16385/j.cnki.issn.1004-4523.2015.05.002

王秀丽（1963—），女，教授，博士生导师。E-mail：545784567@qq.com

马肖彤（1989—），女，博士，讲师。E-mail：maxt215@139.com

2014-07-06；

：2014-11-02

国家自然科学基金面上项目（51278236）；国家科技支撑计划项目（2011BAK12B07）