结构模态振型的径向切比雪夫矩函数描述研究

姜丹丹，臧朝平

（南京航空航天大学能源与动力学院，江苏省航空动力系统重点实验室，江苏 南京210016）

结构模态振型的径向切比雪夫矩函数描述研究

姜丹丹，臧朝平

（南京航空航天大学能源与动力学院，江苏省航空动力系统重点实验室，江苏 南京210016）

利用径向切比雪夫矩函数对结构振动模态振型进行描述，从大量的结构模态振型数据中提取出矩特征值，实现了对模态振型数据的压缩及特征提取，并且利用这些矩特征值可以对振型图像进行很好的振型重建。基于矩特征值的相关分析，可以描述对称结构的重模态，弥补了传统的 MAC对于重模态描述的不足。通过对圆盘结构进行模态试验及有限元仿真计算，验证了利用径向切比雪夫矩函数处理对称结构模态振型的可行性。结果表明：利用径向切比雪夫矩函数可以很好地描述对称结构重模态的特性，并求得重模态之间的转角，这对于进一步利用径向切比雪夫矩进行模型修正及模型确认有重要的指导意义。

模态振型；径向切比雪夫矩；相关分析；重模态；特征提取

引 言

结构的动力学特性在模态域中一般采用固有频率、阻尼比和模态振型来描述。而模态置信准则（Modal Assurance Criterion，MAC）［1］常用于评价有限元模型预测的结果与结构模态测试数据的接近程度，即为有限元模态振型与实测振型夹角的余弦值，是确定两组数据模态对匹配的有用工具，也是有限元模型修 正与 模型 确认 中关 键步 骤［2-3］。由于MAC值将两组模态振型数据的特征信息相似度只用一个参数描述，它的大小受到对比数据点自由度的多少、在结构上的位置等影响。同时，对于大型或者复杂结构，局部或整体的模态振型的变化，用MAC值进行详细描述，也存在困难。尤其是随着现代测试技术的发展，如用连续激光扫描测振仪测量结构模态，理论上，其测点可以无限增加，以获得更加精细、准确的测量数据。然而，这些大量的且存在冗余信息的数据，仅利用MAC进行处理，存在着局限性。实质上，MAC值反映的只是结构模态振型空间描述点上两个数据组的简单对比。如何从大量振型数据中提取出模态的振型特征，进行振型特征间的对比，更具有应用价值。此外，利用MAC值描述对称结构的振动模态相关性时，由于对称结构存在两个或多个频率相近，振型相似但存在一定转角的模态（重模态），MAC值对其相关分析，也受到限制。

近年，将模态振型数据看作一种图像，通过图像模式识别中的矩函数提取结构振动模态振型的特征，并进行振动矩特征相关分析，以改善MAC值对振动模态相关性分析的描述，引起关注。在国外Wang［4-5］等人首先将Zernike矩函数、Tchebichef矩函数成功应用于结构模态振型的特征提取及相关分析中。利用Zernike矩函数对圆盘、矩形板及带有附加质量的圆盘结构进行了分析，提取出在各种情况下的Zernike矩特征值，并进行基于Zernike矩特征值的相关性分析；利用Tchebichef矩函数对矩形复合材料夹层面板进行了矩特征值提取、相关分析及模型修正。在国 内臧 朝平、刘 银 超、贾晴 晴［6-9］等也对Zernike矩函数、Tchebichef矩函数进行了深入研究，并对航空发动机实际结构，如航空发动机轮盘，进行了矩特征值的提取、相关分析及模型修正，将矩函数成功应用于实际工程结构。在图像处理领域，Mukundan［10］等在2005年提出径向切比雪夫矩函数（Radial-Tchebichef moments，RTMs）的概念，并成功地应用于图像特征提取及其重建，之后改进了径向切比雪夫矩函数的算法［11］，利用改进后的算法对图像处理领域中常用的Lenna图像进行矩特征值的提取及图像重建，结果表明利用径向切比雪夫矩函数对图像进行重建，利用较少阶数的矩特征值就可以取得很好的图像重建效果。径向切比雪夫矩函数是由一维切比雪夫多项式与三角函数组合而成，相比于其他矩函数，具有以下优点：（1）核函数满足正交性，提取图像特征时，不存在数据冗余；（2）核函数为离散函数，在离散的图像域内进行计算时，无需进行连续函数离散化的数学处理，不会产生由于核函数为连续函数而带来的离散误差；（3）满足旋转不变性，适用于处理圆形结构。本文将径向切比雪夫矩函数引入到结构动力学的振动模态振型描述中，通过径向切比雪夫矩函数提取振动模态振型的特征信息，进而建立基于模态振型特征信息的矩相关性判定方法，评价有限元模型预测的结果与结构模态测试数据的接近程度，优于结构模态置信准则的相关分析。

本文安排如下：首先，介绍径向切比雪夫（Radial-Rchebichef，RT）矩函数描述模态振型及振型特征提取的方法，将模态振型表示为基于RT矩函数的线性组合；同时，介绍基于模态振型特征信息的矩相关性判定方法；然后，以圆盘结构为例，通过有限元仿真结果和实验测试数据的分析，验证了模态振型RT矩特征值的提取及模态振型矩相关性的分析，并得到了圆盘结构重模态对间的转角关系；最后对全文进行了总结。

1 基于径向切比雪夫矩函数的模态振型描述和矩相关性

1.1 模态振型的径向切比雪夫矩函数

对于像素为N×N的图像，可将其分为个同心圆，圆的编号为r，r=0，1，…，-1，每个同心圆环内所含像素点的个数为mr，假设每个圆环内像素点沿周向均匀分布，每个像素点的角度值θk按下式计算

则图像中每个像素点的极坐标值可用 （r，k）表示。图1为像素值N=10时的示意图。其中mr的取值如表1所示。

表1 mr与r的取值关系Tab.1 The relationship between mrand r

图1 当N=10时，像素点分布示意图Fig.1 The distribution of pixels when N=10

结构的模态振型可以看作像素为N×N的图像，如果用ψ（r，k）表示其在极坐标下的模态振型数据，则模态振型图像的p阶q重RT矩Rpq可以表示为

式中tp（r）为一维p阶切比雪夫多项式。

其中：

通过RT矩变换，可以从模态振型数据中提取出一系列的RT矩特征值，这些特征值构成的模态振型图像的RT矩特征集为：

模态振型图像的p阶q重RT矩Rpq是个复数，若与分别为RT矩的实部与虚部，其具体表达式如下

假设将结构模态振型图像绕中心原点旋转一个角度φ，且图像在旋转过程中保持每个像素点的振动位移值不变，则旋转后振型图像的p阶q重RT矩为

对于上式的复数利用实部与虚部进行表述

Rpq幅值为，可以看出随着振型图像的旋转其幅值不变化，即，也就是说模态振型图像的RT矩具有旋转不变性。且模态振型的旋转角度可以利用下式得到

此特征，可以用于有效求解对称结构的相近模态（重模态）的转角。

1.2 模态振型图像的重建

利用有限数目的RT矩对振型图像进行重建，其重建公式如下

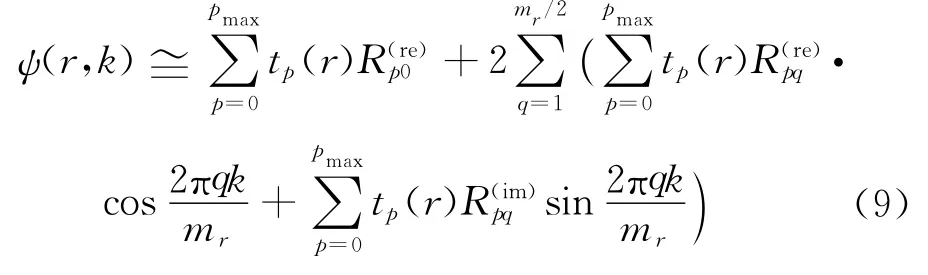
式中pmax为用于重建的矩的最大阶数，为q=0时的RT矩的实部值，与分别为RT矩的实部与虚部。

1.3 矩相关性

工程实际中最常用的模态相关分析方法为模态准信准则（MAC），也被称为振型相关系数，其定义为

式中φei表示实验测试的第i阶模态的振型向量，φaj表示有限元计算的第j阶模态的振型向量，T代表转置。

仿照模态置信准则的定义，利用RT矩特征集的幅值定义的各阶模态振型之间的相关系数为

式中Rei表示实验测试的第i阶模态振型的矩特征集幅值的向量，Raj表示有限元计算的第j阶模态振型的矩特征集幅值的向量，H代表共轭转置。

MAC与RTMAC均为0到1之间的一个数，越接近于1则表示两个模态振型相关性越高，若为0则表示两者没有相关性。另外，参与相关分析的可以是两个不同类型的模型，如有限元/实验之间的相关分析，也可以是相同类型模型间的相关分析，如实验/实验，有限元/有限元之间的分析。

由上文分析可知，对于重模态的振型图像，由于振型向量之间有一定的转角，所以利用MAC进行分析时，重模态振型之间的相关性很低，甚至为0。而重模态对的RT矩值的幅值是相等的，为旋转不变量，所以在利用基于RT矩的相关分析时，重模态之间的相关性很高，可以对重模态振型的特性进行很好的描述。

2 应用实例：圆盘结构振型的 RT矩描述

为了验证RT矩提取结构振型特征的可行性，对一圆盘对称结构进行了模态测试，获得其前16阶固有频率及模态振型。同时通过有限元仿真获得圆盘模态振型的理论解。相关分析分别采用了传统的模态置信准则（MAC）和基于RT矩的相关性分析方法，并对结果进行了比较分析。

2.1 圆盘的有限元模型及模态振型

圆盘实物如图2所示，半径为200 mm，厚度为4 mm，在PATRAN中建立有限元模型如图3所示。有限元单元采用4节点板壳单元，共划分2 521个单元，边界条件为自由-自由状态。圆盘材料参数为密度78 500 kg/m3，泊松比0.24，弹性模量199 GPa。

图2 圆盘实物Fig.2 Disk structure

图3 圆盘有限元模型Fig.3 FE model of the disk

利用NASTRAN求解器求解圆盘有限元模型的前16阶模态，得到其各阶固有频率及模态振型，分别如表2和图4所示。

表2 圆盘有限元模型的各阶固有频率Tab.2 The natural frequencies of FE model prediction of disk

图4 圆盘有限元模型的各阶模态的振型图像Fig.4 Vibration mode shape images of FE model of disk

在圆盘各阶模态振型中可以看出Z为主要振动方向，以Z向振动位移值为灰度值来建立圆盘振型图像，如图5所示。

综合考虑计算效率与重建效果选择p=15，即利用前15阶RT矩特征值对模态振型图像进行重建，其重建振型图像如图6所示。

图7为采用模态置信准则（MAC）计算的模态振型自相关系数（Auto MAC）。可以看出传统的MAC值，对角线上接近1，非对角线上近似为0，反映了各阶模态的自相关特性，但不能表示出对称结构重模态之间的相关性，如第1阶与第2阶模态，第4阶与第5阶模态等，均是频率一致，振型非常相似的相近模态（重模态），只是振型间有一定的转角。

2.2 圆盘的模态测试及实验分析

利用多普勒连续激光扫描测振仪对该圆盘进行模态实验，实验利用锤击激励，圆盘的Z向为主要振动方向，故选择圆盘的Z向为测量方向，边界条件为自由-自由，图8为实验布置图。实验中共布置289个扫描点，可以获得圆盘非常精细的模态振型数据。通过实验测得的前16阶模态的固有频率如表3所示，各阶模态振型如图9所示。

图5 圆盘有限元各阶模态振型的灰度图像Fig.5 Gray level images of FE model of disk

图6 利用p=15重建有限元的模态振型图像Fig.6 The reconstructed mode shape images of the disk underp=15

图7 圆盘有限元模型的Auto MACFig.7 Auto MAC of FE model of the disk

图8 实验布置图Fig.8 Test configuration

图9 圆盘测试前16阶模态振型Fig.9 The mode shape images of the test disk

实验模态振型的灰度值图像如图10所示。同样，选择p=15，即利用前15阶RT矩特征值进行振型图像重建，重建图像如图11所示。

采用传统MAC进行相关分析，结果如图12所示，与有限元分析结果类似，传统 MAC不能很好地对重模态进行描述。下面将采用基于RT矩的相关性分析，利用提取图像的特征矩对模态振型的重模态进行相关性分析。

表3 圆盘模态测试前16阶固有频率Tab.3 The natural frequencies of the test

图10 圆盘测试振型灰度图像Fig.10 Gray level images of the test disk

2.3 圆盘实验/有限元相关分析

为解决上述问题，将图像处理及模式识别中的矩函数引入到结构动力学模态相关分析中。由于RT矩存在旋转不变量，可以对有旋转角度的模态振型图像进行较准确的相关性分析。分别对上述圆盘振动模态的有限元分析和实验测试结果，进行基于RT矩的自相关分析，结果如图13，14所示。可以看出基于RT矩的相关分析方法，无论是计算仿真数据还是实验测试，都可以很好地对重模态进行自相关分析，如模态1与模态2，模态4与模态5，模态6与模态7，等，皆为重模态，在RTMAC中可以很好地看出重模态的两阶模态除了与自身的相关性很高外，两者之间的相关性也很高，这也与实际情况相符。

图11 利用p=15重建测试的模态振型图像Fig.11 The reconstructed mode shape images of the test disk under p=15

图12 实验的Auto MACFig.12 Auto MAC of test

图13 基于RT矩的Auto RTMACFig.13 AutoRTMAC of FE model

利用传统MAC求解得到的实验/有限元的互相关分析结果如图15所示，基于RT矩的相关分析结果如图16所示，表4列出了各阶模态的相关系数，对于第4阶与第5阶模态，第6阶与第7阶等多对重模态，利用RTMAC，其相关系数得到大幅提高，与实际情况相符，很好地描述了其重模态的特性。此外，在利用MAC值进行分析时，若对应阶次的有限元计算结果与实验结果的转角偏差较大，则会出现如表4中所示的第15阶与第16阶匹配时的错阶问题。可以看出利用基于RT矩的相关分析非常适合于分析对称结构的重模态问题。

图14 AutoRTMACFig.14 AutoRTMAC of test

图15 MAC相关分析结果Fig.15 MAC of FE model and test

图16 基于RT矩的相关分析Fig.16 RTMAC of FE model and test

表4 有限元与实验的相关系数Tab.4 The correlation coefficient between FE model and test

图17，18分别表示有限元与实验测试的各阶模态振型图像RT矩的最大主矩的极坐标图，从图中可以看出对于每一组重模态，其最大主矩的幅值相同，相角不同。这也反映了重模态振型相似，但两者间有一定转角的特征。利用两阶重模态最大主矩的角度差，也就可以进一步求得重模态对之间的转角大小。以有限元的模态4与模态5为例，这两阶模态的主矩均为RT13，这两阶主矩的夹角为90°，其最大主矩的重数为3，则

利用此方法可以分别求得有限元模型的所有重模态与实验测试结果的所有重模态的旋转角度，其结果如表5所示，这也是利用基于RT矩的相关分析比传统MAC进行相关分析的一大优势。从表5可以看出有限元计算求得的转角结果与实验得到的结果有很好的一致性。

图17 有限元最大主矩极坐标图Fig.17 The maximal RTM of the FE model

分别对有限元计算结果和实验结果提取RT矩特征值进行比较，图19，20分别为有限元结果与测试结果的矩特征值幅值柱状图，这两幅图中，可以看出各阶主矩的矩特征值的分布有很好的一致性，幅值大小有一定的细微差异。图21为第1阶模态振型的主要矩特征值的幅值柱状图的细化描述，其中黑色表示测试数据的矩特征值幅值，浅色表示有限元计算结果的矩特征值幅值。从图中可以看出，从实验结果提取的矩特征值与从有限元结果提取的矩特征值，其主矩位置一致，幅值有微小差异，这也就反映了实验模态振型图像与有限元计算结果模态振型图像的差异。

图18 实验最大主矩极坐标图Fig.18 ThemaximalRTMofthetest

表5 有限元与实验计算重模态夹角Tab.5 Anglesofthedoublemodes

图19 有限元结果矩特征值柱状图Fig.19 RTMSofFEmodel

图20 测试结果矩特征值柱状图Fig.20 RTMs of the test

图21 第1阶主矩放大比较图Fig.21 The enlarged figure of the comparison of RTMs between the first mode of FE model and test

3 结 论

利用RT矩函数对结构模态的振型图像提取RT矩特征值，可以从大量的振型数据中提取最主要的振型信息，可对振型数据进行有效的数据压缩。对于对称结构，含有重模态，利用传统的 MAC对其进行分析时，不能很好地对重模态进行描述，且仅利用MAC对振型数据进行相关分析时，不能对振型的局部差异进行识别，有一定的局限性。由于RT矩具有旋转不变量，利用基于RT矩的相关分析就可以很好地弥补MAC分析的不足，可以对重模态进行很好的描述，并求得重模态的转角，这对于确定有限元与测试的模态匹配，及进一步的模型修正与模型确认具有重要的理论指导意义。

［1］ Allemang R J，Brown D L.A correlation coefficient for modal vector analysis［A］.Proceedings of 1st IMAC ［C］.Orlando，USA.1982：110—116.

［2］ Zang C，Ewins D J.Model validation for structural dynamics in the aero-engine design process［J］.Frontiers of Energy and Power Engineering in China，2009，3（4）：480—488.

［3］ Ewins D J.Modal Testing：Theory，Practice and Application［M］：Research Studies Press，Ltd.，2000.

［4］ Wang Weizhuo，Mottershead J E，Mares C.Mode shape recognition and fnite element model updating using the Zernike moment descriptor［J］.Mechanical Systems and Signal Processing，2009，23（2）：2 088—2 112.

［5］ Wang Weizhuo，Mottershead J E，Mares C.Finite element model updating from full field vibration measurement using digital image correlation［J］.Journal Sound and Vibration，2010，10（36）：1—22.

［6］ 刘银超，臧朝平.对称结构模态振型的Zernike矩描述方法［J］.振动工程学报，2011，24（4）：369—375. LIU Yingchao，ZANG Chaoping.Mode shape description of a ymmetrical structure using Zernike moment descriptor［J］.Journal of Vibration Engineering，2011，24（4）：369—375.

［7］ Liu Yingchao，Zang Chaoping.Mode shape description of an aero-engine casing structure using Zernike mo-ment descriptors［J］.Journal of Aerospace Power，2011，26（4）：760—770.

［8］ 臧朝平，刘银超.轴对称结构的模态振型描述和模型确认研究［J］.南京航空航天大学学报，2012，44（5）：725—733. Zang Chaoping，Liu Yinchao.Mode shape description and model validation of axisymetric structure［J］. Journal of Nanjing University of Aeronautics&Astronautics，2012，44（5）：725—733.

［9］ 贾晴晴，刘银超，臧朝平.结构模态振型的Tchebichef矩描述方法［A］.中国力学大会-‘2011暨钱学森诞辰100周年纪念大会’［C］.哈尔滨，2011.

［10］Mukundan R，Ong S H，Lee P A.Image analysis by Tchebichef moments［J］.Image Processing，IEEE Transactions on，2001，10（9）：1 357—1 364.

［11］Mukundan R.Radial tchebichef invariants for pattern recognition［A］.TENCON 2005 2005 IEEE Region 10.IEEE，2005：1—6.

Research on Radial-Tchebichef moment description of structural mode shapes

JIANG Dan-dan，ZANG Chao-ping
（Jiangsu Province Key Laboratory of Aerospace Power System，College of Energy&Power Engineering，Nanjing University of Aeronautics&Astronautics，Nanjing 210016，China）

Radial-Tchebichef moment is introduced from image processing and pattern recognition to structural dynamics.Extracting the image features using Radial-Tchebichef moment can effectively compress the full-field modal vibration data with the mode shape＇s most important information retained in the form of Radial-Tchebichef moment description.Meanwhile，the reconstruction of mode shapes using Radial-Tchebichef moment description can yield a good result which means the mode shapes can be well described by using less data.Besides，using Radial-Tchebichef moment description in correlation analysis of the double mode for symmetric structures can overcome the disadvantages of MAC.In this paper，the analysis results of the test and FE model of a disk shows that the double modes can be effectively described and the angle of the double mode can be computed by Radial-Tchebichef moment description，which indicates important guiding significance for the development of the modal updating and validation of symmetric structures.

mode shape；Radial-Tchebichef moment；correlation analysis；double mode；feature extraction

TB123

：A

1004-4523（2015）05-0703-11

10.16385/j.cnki.issn.1004-4523.2015.05.004

姜丹丹（1989—），女，研究生。电话：15850501105；E-mail：dandanjiang@nuaa.edu.cn

臧朝平（1963—），男，教授，博士生导师。电话：（025）84892200-2204；E-mail：c.zang@nuaa.edu.cn

2014-06-19

：2014-10-14

国家自然科学基金资助项目（11372128，51175244）；江苏省高校优势学科建设工程项目（PAPD）；先进航空发动机协同创新中心项目