单层柱面网壳冲击试验研究

丁北斗，吕恒林，李 贤，刘建伟，刘 强

（1.中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州221116；2.中国矿业大学江苏省土木工程环境灾变与结构可靠性高校重点实验室，江苏徐州221116；3.江苏建筑节能与建造技术协同创新中心，江苏徐州221116）

单层柱面网壳冲击试验研究

丁北斗1，2，3，吕恒林1，2，3，李 贤1，2，3，刘建伟2，刘 强2

（1.中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州221116；2.中国矿业大学江苏省土木工程环境灾变与结构可靠性高校重点实验室，江苏徐州221116；3.江苏建筑节能与建造技术协同创新中心，江苏徐州221116）

通过单层柱面网壳模型在冲击物作用下试验，研究单层柱面网壳在冲击作用下的动力响应和动力稳定性。利用动态应变仪和力、位移和加速度传感器，获取柱面网壳模型在冲击物作用下的冲击力、杆件应变、位移及加速度时程曲线。根据不同冲击力幅值与测点位移的对应关系，对网壳模型失效形式和破坏形态进行了动力稳定性分析并确定其稳定承载力。结果表明，实验测得的冲击荷载为三角脉冲荷载形式，持续作用的时间为15～35 ms，幅值和脉宽随冲击力增大而增大且与网壳结构的刚度性能有关。柱面网壳在冲击荷载作用下存在全局敏感性和局部敏感性杆件，模型具有较大的后屈曲抗冲击能力，在顶点垂直冲击下没有发生连续断裂。基于ANSYS/LS-DYNA建立了精细化试验模型，模拟单层柱面网壳的失效模式并与试验结果对比，验证了数值模拟方法的有效性。

冲击动力响应；柱面网壳；动力稳定；模型试验

引 言

空间网格结构基于冲击荷载作用下的力学性能和破坏形态所进行的研究，目前还涉及较少，冲击荷载为三角脉冲荷载，其研究对冲击、爆炸作用下网壳动力破坏研究具有重要参考价值。由于冲击荷载研究相对于其他形式研究较为国难，进行冲击加载试验设备也较少，导致目前对于网壳结构受冲击后物理试验研究较少。国内只有太原理工大学和哈尔滨工业大学拥有垂直落锤冲击设备，不少学者利用该设备展开了对于冲击荷载下网壳结构受冲击荷载研究。试验设备采用落锤式撞击，研究了K8型单层球面网壳的动力响应和失效模式［1-4］。对其他结构形式，更多的是基于ANSYS LS-DYNA平台进行数值模拟分析［5-10］。柱面网壳结构广泛应用于工业生产实际工程中，遭受到外物冲击概率可能较大，而目前对柱面网壳结构在冲击荷载作用下的动态响应和失效模式缺乏试验研究。本文对单层三向柱面网壳结构试验模型在冲击试验下动态响应进行研究，以获取单层柱面网壳在冲击荷载作用下动态响应和失效模式，为该类柱面网壳结构抗连续性倒塌提供有效依据。试验目的如下：（1）研究单层柱面网壳在冲击荷载下的动力响应，主要测试试验数据有节点位移、加速度和关键杆件的应力响应；（2）研究单层柱面网壳在不同冲击点下的动力响应，获取单层柱面网壳结构的最大冲击动力响应，以此确定单层柱面网壳的最易失效冲击点；（3）研究单层柱面网壳在冲击荷载下的破坏形态，为数值模拟对比分析和指导实际工程的抗冲击性和结构抗连续倒塌提供依据。

1 试验方案与试验内容

试验在自行研制的试验装置上进行，冲击高度可达5 m，相应竖向冲击速度可达9.89 m/s，试验装如见图1所示。本次试验模型采用单层柱面三向网壳结构，所有杆件均用无缝钢管Φ10 mm×2 mm，其屈服强度为318 N/mm2，极限抗拉强度为410～550 N/mm2，伸长率为25%，弹性模量约为E=2.1×105N/mm2，泊松比为0.3，杆件节点通过节点板焊接在一起。该单层柱面三向柱面网壳，跨度为1 500 mm，矢高为375 mm，纵向长度为2 000 mm，矢跨比为1/4。

图1 试验加载示意图Fig.1 Test loading scheme

冲击物通过自由落体运动，产生速度，竖直冲向置于模型壳顶的力传感器（应变式），力传感器和杆件产生随时间而变化的动应变。试验中通过改变落锤质量和下落高度的方式获取大小不同的冲击作用，模拟多种工况，并通过应变仪测得质量块对网壳冲击作用的力、杆件应变和关键节点位移、加速度时程曲线，并观察相应的柱面网壳结构变形和破坏状态。在试验操作平台处，通过突然释放，实现冲击加载，冲击完毕后，由拉索自锁，以避免冲击物对网壳结构二次冲击加载。

图2为应变片和传感器的粘贴位置，应变片采用全桥接法，在模型杆件中部上下两面粘贴两处应变片，并外设两片补偿片，以测得杆件的轴向力时程曲线，传感器分为加速度传感器和位移传感器。为了后文叙述方面，杆件编号等同应变片编号，A～F测点为位移传感器和加速度传感器布置位置，因位移传感器形状较大，为保护其免受冲击损伤，冲击试验时，对应冲击测点处的位移传感器拆除，仅保留加速度传感器。

图2 应变片及传感器布置图Fig.2 Layout of strains and sensors

试验主要对柱面网壳模型进行弹性冲击试验和动力失稳冲击试验，弹性试验主要目的是探求单层柱面网壳受冲击后的动力响应规律，探求引起动力响应的最易冲击点，动力失稳试验主要是研究柱面网壳结构的失效模式和破坏形态。本次试验共进行11个工况的冲击试验，工况1～9进行弹性冲击试验，分别在A，B，C三个冲击点，以不同的高度分别进行；工况10～11进行动力失稳冲击试验，在B冲击点，以1.8 m和5 m的高度分别进行冲击试验，具体实验方案如表1所示。

表1 冲击试验参数Tab.1 Impact test parameters

2 试验结果

2.1 冲击力时程曲线

试验记录了各工况的冲击力时程曲线，各工况撞击力的特征参数如表1所示，Fi，max为冲击力最大值，ti，max为冲击力最大作用时刻值，td为冲击力持续时间。弹性失稳前工况1、失稳时大变形阶段的工况10典型冲击力时程曲线见图3所示。试验时工况1～10均测试了应变、位移和加速度数据，工况11为了保护位移传感器，拆除了位移传感器，仅测试了应变和位移数据。

表2 冲击B点试验现象描述Tab.2 Description of impact test phenomenon on point B

从图3可以看出，冲击荷载持续的时间非常短暂，当冲击作用较小时，模型杆件处于弹性工作状态，整个结构处于小变形状况下，此时的冲击接触时间约为15～30 ms。例如工况1冲击力荷载形态为图3（a）所示曲线，冲击力荷载形态呈陡峭的三角脉冲状，落锤明显；随着冲击荷载的增大，冲击力持续时间逐渐增长，但增大幅度不大，直到冲击作用继续加大到20 kg时，冲击荷载持续时间有所增长，约为35～40 ms，例如工况10冲击力荷载形态为图3（b）所示曲线，其特征为很短时间内达到峰值，之后存在一个冲击力峰值逐渐衰减直至为零的过程，冲击力三角脉冲宽度比工况1稍有增加。

图3 冲击力时程曲线Fig.3 History curves of impact force

2.2 应力时程曲线

根据三向柱面网壳结构选取若干沿纵向和斜向杆件应力时程曲线图如图4所示，从表2和图4可以得出落锤冲击下，柱面网壳杆件应力时程响应具有如下传播规律：

（1）杆件应力响应，都是自冲击点位置（壳顶节点）开始，继而向四周传播开来，即离冲击点越近位置，其杆件产生响应时刻越早且幅值越大，离冲击点越远的位置，其杆件产生响应时刻稍晚且幅值较小。尽管应力传播响应存在先后，离冲击点不同位置存在滞后现象，但整个传播过程仍极为短暂，从壳顶开始响应到响应传遍整个网壳，耗时时间在微秒级别，与文献［1］描述基本相同。

（2）在冲击荷载作用下，杆件应力的拉压关系和静力荷载作用下基本相同，但由于制造误差的原因，对称杆件的响应并不一致，冲击点越高，动态响应越明显，甚至会使杆件应力拉压力学性质发生改变。

（3）柱面网壳结构在不同冲击点处对不同杆件的作用不同，如杆件1在A点5 kg冲击时，杆件轴力峰值达到15 995 N，此时杆件存在弯曲现象，在B 点5 kg冲击时降到1 696 N，在C点5kg冲击时降到3 518 N，可见杆件1在冲击点A处动态响应最明显，随着冲击点距离较远，冲击力显著下降，如见图4所示。

（4）柱面网壳杆件在冲击作用下动态响应存在局部敏感性和全局敏感性构件，对于柱面网壳模型，横向周边位置的杆件1在不同冲击点的冲击作用下，其冲击作用后的动态响应均很明显，具有明显的全局敏感性特点，杆件22在A，C点冲击时，动态响应不明显，仅在B点冲击时反应明显，当B点20 kg，高度5 m冲击时，杆件22杆件屈曲，局部失稳，该杆件具有明显的局部敏感性特点，详见图4～6所示。

（5）柱面网壳杆件在不同冲击点作用下杆件应力动态响应的受力特点会发生转化，杆件应力幅值会发生变化，甚至有些杆件的受力性质也发生变化，从受压变为受拉或从受压变为受拉，存在跳跃现象。如杆件1在不同冲击点冲击作用下，杆件应力始终处于受拉状态，但杆件应力幅值在A点受冲击时幅值最大，在C点受冲击时幅值最小。冲击点A处杆件18应力很小，杆件19为压应力，在冲击点B处杆件18明显受压，杆件19几乎不受力，在冲击点C处杆件18受压应力变小，杆件19则变为受拉构件，如图7所示。

图4 在A，B，C点冲击时杆件1，13，31应力时程曲线（m=5 kg，h=0.8 m）Fig.4 Stress history curves of member 1，13，31 of impacting on point A，B，C（m=5 kg，h=0.8 m）

图5 在A，B，C点冲击时杆件22，14，7应力时程曲线（m=5 kg，h=0.8 m）Fig.5 Stress history curves of member 22，14，7 of impacting on point A，B，C（m=5 kg，h=0.8 m）

图6 在B点冲击时杆件1，13，31，22，14，7，18，19，20应力时程曲线（m=20 kg，h=1.8 m）Fig.6 Stress history curves of member 1，13，31，22，14，7，18，19，20 of impacting on point B（m=20 kg，h=1.8 m）

图7 在A，B，C点冲击时杆件18，19，20应力时程曲线（m=5 kg，h=0.8 m）Fig.7 Stress history curves of member 18，19，20 of impacting on point A，B，C（m=5 kg，h=0.8 m）

2.3 位移、加速度时程曲线

在同一冲击区，随着冲击物重量和高度增加，各测点变形在增大，在每一次冲击过程中各点的变形见各测点变形时程图，可以发现，柱面网壳结构冲击后，冲击点处变形最大，然后逐渐向其周围扩散，冲击力较大时，冲击点处形成局部凹陷，变形未扩展至整个柱面网壳，仅局部杆件发生屈曲失效，如图8所示。

在B点处冲击网壳结构模型时，离B点较近测点A，C，D很快就产生位移峰值，随后测点E和F稍后产生位移峰值，从位移时程曲线可以看出，远离冲击点B的测点F位移在滞后很小时间段后，有较大变形，呈现出一个变形波传递特征，如图9所示。

同测点位移时程曲线一样，随着冲击点的重量和高度的改变，各测点的加速度也呈增大趋势，以冲击B点时测点A的加速度为例，如图10所示，当冲击高度在h=0.05，0.2 m时测点B加速度分别为15和30 m/s2；当冲击高度为h=0.8 m，测点B的加速度因估计不足，已经超过量程范围，相比较于h=0.2，0.8 m的加速度时程曲线更密集。

3 试验模型数值模拟分析

空间网格结构属于多自由度复杂体系，在受到外界冲击时，结构具有几何大变形和材料弹塑性问题，且冲击荷载随时间变化极快且持续时间短，在短暂时间内产生的力学行为与准静态有差别，需要考虑动力响应时程特性。本文首先建立网格结构动力平衡方程，然后采用中心差分动力显式计算方法求解非线性动力平衡方程［8，12］，即数值模拟分析机理。ANSYS/LS-DYNA是功能齐全的几何非线性（大位移、大转动和大应变）、材料非线性和接触非线性分析程序，它以Largrange算法为主，兼有ALE和Euler算法，以显示求解为主，兼有隐式求解功能，可以为冲击荷载下网壳结构失效模式和动力响应数值模拟有效性提供验证。

图8 不同高度测点A，B位移时程曲线Fig.8 Displacement history curve of measuring point A，B under different heights

图9 在B点处冲击各测点位移时程曲线Fig.9 Displacement history curve of measuring points of impacting on point B

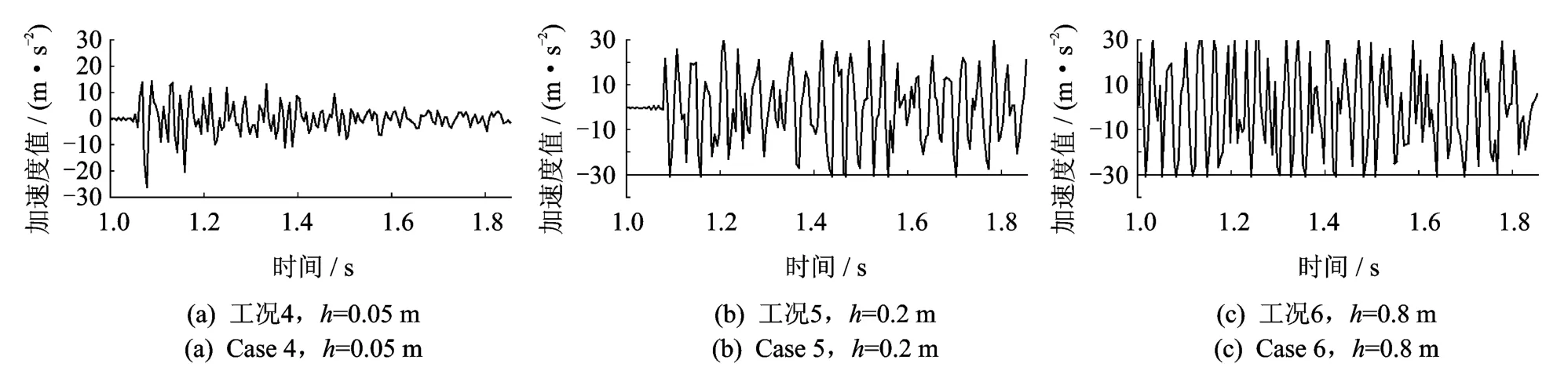
图10m=5 kg时冲击B点测点A加速度时程曲线Fig.10 Acceleration history curve of measuring point A of impacting on point B（m=5 kg）

3.1 动力平衡方程

对网格结构有限元离散后，建立网格结构振动方程为

式中m表示质量矩阵，c表示阻尼矩阵，k表示刚度矩阵，p表示荷载矩阵，u表示位移矩阵。

采用中心差分法求解结构振动方程（1），用位移的线性组合来近似表示速度和加速度。把时间历程T分为许多等分的时间步长Δt，并记ut+Δt=ui+1，ut=ui，ut-Δt=ui-1。根据泰勒级数前二阶近似式可得t时刻速度、加速度表达式：

将式（2）代入式（1）得到

式中

从而通过式（3）可以求出t+Δt时刻的位移。在动力学问题中初始位移u0和初始速度˙u0属于已知条件，通过u0，˙u0可以得出利用中心差分法的初始迭代值¨u0和u-1，如下式

3.2 有限元模型

基于ANSYS/LS-DYNA对试验模型实测的节点坐标进行建模，冲击重锤部分采用实体单元SOLID164，试验模型杆件采用BEAM161梁单元模拟，除冲击点外的节点板采用MASS166模拟。试验工况对柱面网壳顶部冲击加载，速度施加通过定义冲击物的初始速度，而单元接触采用点面接触、自动面面接触。

对于冲击荷载作用下的弹塑性材料，需要考虑材料在冲击荷载作用下的屈服强度与瞬时应力随应变率变化而变化的行为。在结构冲击问题中，常采用理想塑性模型进行模拟，并考虑应变率影响，实际上，在结构塑性动力学领域内，通过Cowper-Symonds方程给出的是应变率和材料流动应力之间的关系式中σ0为常应变率的屈服应力；˙ε＇为有效应变率；C和P为应变率参数；fh为基于有效塑性应变的硬化参数。

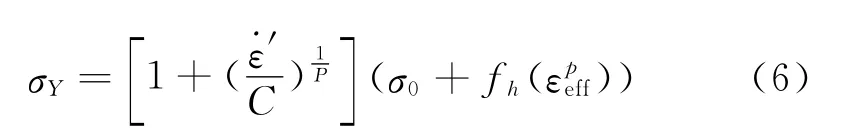
图11 钢管分段线性材料模型曲线Fig.11 The piecewise linear material modal of steel tube

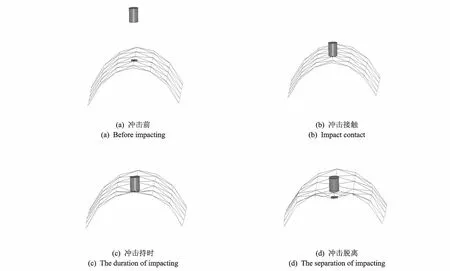
图12 冲击阶段数值模拟Fig.12 The numerical simulation of impacting phase

梁单元的材料模型采用分段线性塑性模型，从塑性阶段取较为明显转折点处作为分段线性模型的分界点，定义出适合钢管的分段线性模型如图11所示。ANSYS中的BEAM161单元能自动考虑杆件屈曲变形，杆件断裂则根据所设定材料模型属性来实现，采用双线性强化模型可以通过设定材料极限应变来判断杆件失效，即当杆件某一积分点应变达到极限应变时，软件自动认为此处失效，在计算过程中，极限应变不区分拉压特性，模拟时失效应变取值为0.25［7-8］。重锤、力学传感器和节点板不作为具体的研究对象，采用了刚体材料模型建立。

3.3 数值分析结果与试验结果对比

对代表性工况的试验模型数值模拟和试验结果的破坏形态，冲击力时程曲线以及典型部位的位移和应力时程曲线进行比较，用以演示数值分析过程和分析真实物理试验与数值模拟的差距，以此来验证数值模拟有效性。

基于ANSYS/LS-DYNA对工况6和工况10进行模拟，冲击点为B，冲击过程如图12所示。工况6中，重锤自由下落首先接触力传感器，进而把冲击力传递到网壳节点上，节点处产生向下偏移位移，网壳结构两侧产生轻微扩张。由于网壳刚度较大，重锤与传感器被反弹分离，冲击过程完成，整体结构保持完整。工况10重锤自由下落，直接冲击节点板，冲击发生时冲击点下陷并带动周围节点产生偏移，与冲击点相连的杆件产生弯曲变形，结构最终呈现局部凹陷状态，如图13所示。

图13 数值模拟与试验破坏最终形态对比Fig.13 The comparison of final deformation between numerical simulation and experiment

图14～16为工况6作用下数值模拟和试验结果冲击力时程曲线以及典型部位位移和应力时程曲线进行比较。从图14冲击力时程曲线比较中可以看出，数值模拟与试验结果有一定误差值，工况6试验误差为523.2 N，数值模拟的结果要略大于物理试验的结果，但是冲击力时程曲线的运动趋势具有相似性，都基本呈现三角形脉冲形式，冲击持时阶段冲击力值急剧增长，随后下降。

图14 冲击力时程曲线对比（m=5 kg，h=0.8 m）Fig.14 The comparison of impact force time history curve

图15，16对比主要节点和杆件数值模拟和试验结果位移和应变时程曲线，两者也表现出相同趋势：冲击节点位移值急速增大，节点位移时程曲线呈现“U”型，冲击完成后，节点在平衡位置处自由振动。例如C点最大位移值，试验结果为-21.87 mm，数值模拟结果为-17.03 mm，两者相差4.84%，远离冲击点的杆件5最大轴向应变，试验结果为132.2 με，数值模拟结果为310με；由此可知，数值模拟结果和试验结果的位移时程图趋势相同，但是数值结果有一定差异。

3.4 失效机理分析

综上单层网壳结构冲击荷载下数值模拟和试验研究表明，冲击发生时，柱面网壳冲击区域响应敏感，冲击区内节点速度、位移瞬时增加，从而使冲击区域动能和应变能急剧增加，造成冲击区域杆件变形或损伤，导致冲击区域应变能和动能减少。由位能转化的杆件应变能和变形则会以应力波方式逐渐由冲击区向其他区域扩散，从而实现由局部向整体蔓延，柱面网壳逐步进入凹陷，进而整体结构发生较大变形或坍塌。

图15 C点位移时程曲线对比（m=5 kg，h=0.8 m）Fig.15 The comparison of node C displacements time history curve

4 动力稳定性研究

4.1 冲击失稳与破坏

为寻求冲击作用下网壳逐渐破坏过程和基于变形后抗冲击性能，试验中采用2种质量冲击物（分别为5和20 kg）和多种起落高度（h=0.05，0.2，0.8，1.8，5.0 m），对模型开展了弹性阶段和破坏阶段的跟踪试验，柱面网壳结构在B点冲击荷载下失稳破坏试验捕捉到的临界情况如表2所示。

图16 5号杆件应变时程曲线对（m=5 kg，h=0.8 m）Fig.16 The comparison of member strain time history curve

试验表明，当网壳模型在弹性冲击荷载作用下，网壳结构整体处于弹性响应状态，也就是当冲击作用结束后，网壳经过往复振动，最终回到原有平衡状态，没有产生残余大变形。当网壳模型在破坏性冲击荷载作用下，在不同冲击点处冲击物质量为5 kg，下落高度为0.8 m时，冲击作用结束后，网壳不能再回到原始平衡状态，壳顶节点产生凹陷，柱面网壳出现第一次局部动力失稳现象，存在残余变形。在A点0.8 m高度冲击时，冲击荷载峰值为1.765 k N；B点0.8 m高度冲击时，冲击荷载峰值为2.025 k N；C点0.8 m高度冲击时，冲击荷载峰值为1.874 k N，B点冲击荷载持荷时间稍长为30 ms，网壳最大变形达到43 mm。

继续加大冲击作用，冲击物质量加大到20 kg，高度达到1.8 m时冲击点位置下陷变形达到73mm，冲击失稳临界荷载为3.497 k N，模型发生第2次冲击局部动力失稳（如图6所示）。当下落高度达到5.0 m时，柱面网壳变形继续增大，为避免试验仪器受损，此时位移传感器和力传感器拆除，根据试验结束后实际网壳测点测量，位移达到150 mm，此时仍然没有发生杆件断裂的现象，模型已进入弹塑性状态，可近似认定其为第3次局部失稳。

表3 冲击力-位移最大值表Tab.3 Impact force-maximum displacement

从试验结果看出，模型网壳发生第1次和第2次动力失稳后，虽然其几何形状发生了变化，其受力性能从薄膜受力状态转变为薄膜和弯曲受力混合状态，部分杆件发生拉压转换。尽管如此，结构并没有连续破坏，仍然具有屈曲后承载能力。继续冲击柱面网壳，基于两次失稳后的网壳变形进一步加大，已进入弹塑性阶段，第2次动力失稳屈曲承载力达到第1次动力失稳的1.5倍，这说明模型网壳首次失稳后，仍具有很强的后屈曲抗冲击能力，网壳没有发生连续倒塌的现象，第3次动力失稳时，柱面网壳节点位移超过了15 cm，达到了整个矢高的近1/2。

本次试验考虑到试验中冲击物的冲击速度较小，属于低速冲击的范围，没有考虑惯性效应和波动问题，因此本实验的失稳现象主要由冲击锤的动量转化为网壳冲击点处的冲量来转化的。柱面网壳结构在第1次动力失稳和第2次动力失稳主要的都是局部弹性失稳，一旦杆件转化后的冲量释放完毕，除有部位位移残留外，结构大部分恢复到原来形状，第3次动力失稳由于动量过大，导致网壳结构杆件屈曲不能恢复，形成网壳结构局部屈曲破坏，柱面网壳结构模型破坏试验前后对比如图17所示。

图17 柱面网壳结构模型动力失稳试验前后对比Fig.17 Comparison before and after model dynamic buckling testing of cylindrical shell

4.2 动力稳定性判别原则

郭海山，沈世钊［11］以网壳结构某特征节点位移作为判别指标，通过荷载幅值结构特征点位移曲线来判断结构的动力稳定性，结构特征点通常取某一荷载幅值下的结构最大位移点。本文参照这些准则思想，以柱面网壳结构冲击作用后节点位移作为判别指标，通过冲击力荷载幅值-结构节点位移曲线来判断结构的动力稳定性。结构节点通常取某一冲击工况下的冲击点附近的网架结构测点。网壳结构因冲击荷载发生局部失稳时，冲击点附近测点位移均会受其影响，同一冲击力荷载幅值下不同测点位移曲线能够反映网壳结构某冲击点附近区域结构局部失稳导致结构整体失稳全过程。本文以网壳结构在B冲击点，绘制不同冲击力荷载幅值下测点A～F的冲击力幅值-测点位移图，见图18和表3所示。可见在m=5 kg，h=0.8 m时，力-位移曲线已经出现拐点了，表征网壳冲击作用下的第1次动力失稳；在m= 5 kg和h=1.8 m，冲击力-位移曲线已经出现第2次拐点，表征网壳冲击作用下的第2次动力失稳。

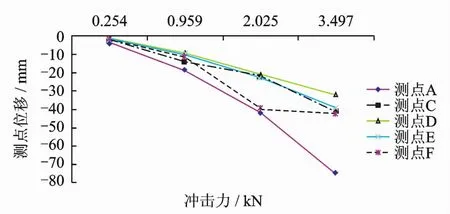
图18 冲击力-测点位移图Fig.18 Curves of impact force-measuring displacement

5 结 论

对柱面网壳结构模型进行了弹性和破坏性冲击试验，得到以下结论：

（1）实验测得的冲击荷载为三角脉冲荷载形式，持续作用时间为15～30 ms，幅值和脉宽随冲击力增大而增大且与网壳结构的刚度性能有关，网壳结构达到动力失稳时，其冲击接触时间有增大趋势。

（2）柱面网壳结构在冲击荷载作用下，动态响应存在局部敏感性和全局敏感性杆件，主要受力杆件是柱面网壳结构中局部敏感度和全局敏感度较大杆件承受，对动态响应敏感度较大杆件区域的位移、应力和加速度幅值均较非敏感区有明显区别。

（3）柱面网壳结构中杆件在不同冲击点作用下杆件应力动态响应受力特点会发生转化，杆件在不同冲击点作用下，杆件应力幅值会发生变化，甚至有些杆件的受力性质也发生变化，从受压变为受拉或从受压变为受拉，存在跳跃现象，局部弹性失稳或屈曲失稳区域的测点也具有类似波动跳跃现象。

（4）当质量为5 kg落锤，从0.8 m高度自由落体冲击网壳壳顶时，网壳顶发生第一次动力失稳，不同冲击位置，冲击临界荷载不同，冲击A点时为1.765 k N，冲击B点时为2.025 k N，冲击C点时为1.874 k N。在冲击点B处，当落锤质量继续加大到20 kg，下落高度达到1.8 m时，壳顶测点A位移达到73 mm，模型发生弹性屈曲，临界冲击荷载达到3.497 k N。在冲击点B处，当落锤质量保持20 kg不变情况下，当下落高度达到5.0 m时，壳顶测点A位移达到150 mm，结构在原有弹塑性屈曲下继续失稳，仍然没有杆件断裂，说明柱面网壳结构具有较强抗冲击能力。

（5）本次试验柱面网壳经历3次失稳，第1和第2次均为弹性失稳，第3次为局部屈曲失稳，模型网壳弹性失稳后，仍具有很强的后屈曲抗冲击能力，没有发生连续性倒塌现象，发生局部屈曲失稳时，部分杆件达到塑性状态时，对应测点位移（壳顶）超过了150 mm，达到整个矢高的1/2，说明其具有较大的抗冲击变形能力。

（6）基于ANSYS/LS-DYNA有限元分析平台，能够模拟试验模型受冲击荷载作用下复杂动力过程。从宏观角度重现试验模型的局部凹陷失效特征，从微观力学的角度揭示了杆件的内力变化特征，冲击力特征值、节点位移、杆件轴向应变与试验结果趋势吻合，验证了数值模拟的有效性。

［1］ 李海旺，郭可，魏剑伟，等.撞击载荷作用下单层球面网壳动力响应模型实验研究［J］.爆炸与冲击，2006，26 （1）：39—45. Li Haiwang，Guo Ke，Wei Jianwei，et al.The dynamic response of a single-layer reticulated shell to drop hammer impact［J］.Explosion and Shock Waves，2006，26（1）：39—45.

［2］ 郭可.单层球面网壳在冲击荷载作用下的动力响应分析［D］.太原：太原理工大学，2004. Guo Ke.Dynamic analysis of singgle-layer reticulated shells under impact［D］.Taiyuan：Taiyuan University of Technology，2004.

［3］ 史俊克.K8型单层网壳在撞击荷载作用下的动力响应研究［D］.太原：太原理工大学，2005. Shi Junliang.Dynamic response research on K8 singlelayer reticulated dome under impact［D］.Taiyuan：Taiyuan University of Technology，2005.

［4］ 王多智，范峰，支旭东，等.单层球面网壳抗冲试验研究［J］.建筑结构学报，2011，32（8）：34—41. Wang Duozhi，Fang Feng，Zhi Xudong，et al.Experimental study on single-layer reticulated dome under impact［J］.Journal of Building Structures，2011，32 （8）：34—41.

［5］ 陆新征，江见鲸.世界贸易中心飞机撞击后倒塌过程的仿真分析［J］.土木工程学报，2001，34（6）：8—10. Lu Xinzheng，Jiang Jianjing.Dynamic finite element simulation for the collapse of world trade center［J］. China Civil Engineering Journal，2001，34（6）：8—10.

［6］ 赵振东，钟江荣，余世舟.钢混结构物受外来飞射体撞击的破坏效应研究［J］.地震工程与工程振动，2003，23 （5）：89—94. Zhao Zhendong，Zhong Jiangrong，Yu Shizhou.Study on damage to reinforced concrete structures by impacting of an aircraft［J］.Earthquake Engineering and Engineering Vibration，2003，23（5）：89—94.

［7］ 范峰，王多智，支旭东，等.K8型单层球面网壳抗冲击荷载性能研究［J］.工程力学，2009，26（6）：75—81. Fang Feng，Wang Duozhi，Zhi Xudong，et al.Performance for Kiewitt 8 single-layer reticulated domes subjected to impact load［J］.Engineering Mechanics，2009，26（6）：75—81.

［8］ 王多智.冲击荷载下网壳结构的失效机理研究［D］.哈尔滨：哈尔滨工业大学，2010：94—115. Wang Duozhi.Failure Mechanism of reticulated Shells under impact［D］.Harbin：Harbin Institute of Technology，2010：94—115.

［9］ Karagiozova D，Alves M.Transition from progressive buckling to global bending of circular shells under axial impact—Part I：Experimental and numerical observations［J］.International Journal of Solids and Structures，2004，41：1 565—1 580.

［10］Karagiozova D，Alves M.Transition from progressive buckling to global bending of circular shells under axial impact—Part II：Theoretical analysis［J］.International Journal of Solids and Structures，2004，41：1 581—1 604.

［11］郭海山，沈世钊.单层网壳结构动力稳定性分析方法［J］.建筑结构学报，2003，24（3）：1—9，49. Guo Haishan，Shen Shizhao.Analysis method of dynamic stability of single-layer reticulated domes［J］. Journal of Building Structures，2003，24（3）：1—9，49.

［12］Anil K.Dynamic of Structures：Theory and Application to Earthquake Engineering［M］.2nd ed.Beijing：Tsing Hua University Press，2005：171—172.

Experimental study on single-layer cylindrical reticulated shell under impact force

DING Bei-dou1，2，3，LÜHeng-lin1，2，3，LI Xian1，2，3，LIU Jian-wei2，LIU Qiang2

（1.State Key Laboratory for Geomechanics&Deep Underground Engineering，Xuzhou 221116，China；2.Jiangsu Key Laboratory of Environmental Impact and Structural Safety in Engineering，China University of Mining and Technology，Xuzhou 221116，China；3.Jiangsu Collaborative Innovation Center for Building Energy Saving and Construction Technology，Xuzhou 221116，China）

Through the experiment for a single-layer cylindrical reticulated shell under impact forces，this paper is intended to study the dynamic response and the dynamic stability of a single-layer cylindrical reticulated shell.The time history plots of the impact force，axial stress，node displacements and accelerations have been obtained using the dynamic strain gauge，force sensor，displacement sensor and acceleration sensors.According to the corresponding relationship between the different impact force amplitudes and the measured point displacements，the failure modes and forms of the reticulated shell model in terms of the dynamic stability are analyzed and the stability bearing capacity is determined.The results show that the impact force on the model takes the shape of triangular impulse and the acting periods of the impact vary from 15 to 30 ms，whose amplitude and width increase with the impact force and both are closely related with the model stiffness.There are global and local sensitivity rods for cylindrical reticulated shell under impact loads，which show strong shock resistance ability at post buckling while no continuous fracture under the vertex vertical impact.The detailed test model is established based on ANSYS/LS-DYNA in which the failure mode of the single-layer cylindrical reticulated shell has been simulated.After comparing the simulation results with the experimental results，the validity of the numerical simulation method is verified.

impacting dynamic response；cylindrical reticulated shell；dynamic stability；model test

TU312+.3

A

1004-4523（2015）05-0692-11

10.16385/j.cnki.issn.1004-4523.2015.05.003

丁北斗（1973—），男，博士，副教授。电话：15952228119；E-mail：dbdstar@163.com

2014-04-10；

：2015-06-08

国家自然科学基金资助项目（51008300，51478459）；江苏省自然科学基金资助项目（BK2011221）；江苏省土木工程环境灾变与结构可靠性重点实验室开放基金资助项目（JSKL2012YB09）；江苏建筑节能与建造技术协同创新中心开放基金青年项目（SJXTQ1524）