一种双横臂独立悬架动力学模型验证的新方法*

龚海清 杨啟梁 胡溧 袁爽

（武汉科技大学）

一种双横臂独立悬架动力学模型验证的新方法*

龚海清 杨啟梁 胡溧 袁爽

（武汉科技大学）

利用某轻型客车的CATIA三维设计数模进行运动仿真，得到悬架线刚度，并与试验结果进行对比，验证了运动仿真结果的正确性。在ADAMS/Car中建立了双横臂扭杆弹簧独立悬架动力学模型，进行动力学仿真计算得到悬架的线刚度，并通过与CATIA中运动仿真计算所得的线刚度对比分析，验证了动力学模型的正确性。该方法同样适用于其它类型独立悬架的动力学模型验证。

1 前言

在汽车性能的动力学仿真计算中，悬架系统的建模比较复杂，其建模精度直接影响仿真结果的正确性。为了保证悬架系统模型的正确性，通常需要利用试验数据来进行模型验证，而在缺少试验验证的条件下，如何验证仿真模型的正确性是目前还没有得到很好的解决[1-4]。采用扭杆作为弹性元件的双横臂扭杆弹簧独立悬架，可以通过合理选择空间导向杆系铰接点的位置及导向臂的长度，使得悬架具有合适的运动特性，保证车辆具有良好的行驶平顺性和操纵稳定性[5,6]，在各种轻型车辆中得到广泛的应用。文中以某轻型客车的双横臂扭杆弹簧独立悬架为例，利用悬架在CATIA中的三维设计数模进行运动仿真分析，得到悬架线刚度，并与试验测试的线刚度进行对比来验证其正确性。然后，在ADAMS/Car中建立悬架动力学模型，进行动力学仿真计算得到悬架线刚度，并与CATIA中计算的线刚度进行对比，以此验证动力学模型的正确性。

2 双横臂独立悬架线刚度计算理论

典型双横臂扭杆弹簧独立悬架拓扑结构简图[7]如图1所示，其中，DE为转向节，FG为主销，GH和GI分别为上横臂的前、后横臂，FK和FJ分别为下横臂的前、后横臂，IL为上置扭杆弹簧。

由于双横臂扭杆弹簧独立悬架的线刚度主要与扭杆的结构和导向机构的形式相关，针对扭杆弹簧，不考虑系统中的摩擦损失时，由虚位移原理可知：

式中，F为车轮的垂向激励力；M为作用在扭杆弹簧上的扭矩；dz为车轮轮心垂向虚位移；dθ扭杆弹簧在扭矩作用下的虚位移转角。

由式（1）可得

式（2）两边对位移z求导，根据悬架线刚度的定义可得悬架线刚度的理论计算式：

式中，θ为扭杆弹簧扭转角；K为扭杆弹簧刚度。

式（3）只需要得到扭杆弹簧扭转角、扭转角对位移分别求1阶导、2阶导以及扭杆弹簧刚度，就可以较准确的计算出车轮跳动在任何位置时双横臂扭杆弹簧独立悬架线悬架刚度值Kl。因此，在任何具有运动仿真功能的CAD软件中均可实现。

3 CATIA中悬架的线刚度计算

某轻型客车的前双横臂扭杆弹簧独立悬架的CA⁃TIA三维数模如图2所示。在CATIA中进行运动学分析时，需要对悬架系统进行适当的处理：弹性元件（橡胶衬套等）用理想化的运动副来代替，并在运动仿真时不考虑弹性元件的变形[8]；定义各部件间的运动关系，如上下横臂与车架之间以旋转副连接，上下横臂与主销之间、转向横拉杆与车架之间均以球面副连接。用DMU Kinematics（运动机构）模块进行运动学仿真分析时，在转向节轴心线处设置测量基准点、建立参考轴系、设置传感器，并在上横臂与车架连接的旋转副处添加旋转驱动。整个机构定义完成以后只有2个自由度，分别对应着转向轮的左右运动和上下跳动。

通过运动模拟，传感器测得扭杆弹簧扭转角与车轮轮心跳位移关系曲线如图3所示；将扭转角曲线对车轮轮心垂向跳动位移分别求1阶导、2阶导，其曲线如图4、5所示。

将图3～5中的扭转角、扭转角的1阶导、扭转角的2阶导曲线数据和扭杆弹簧刚度K=101.41 N/mm代入（3）式，在Matlab中计算拟合悬架线刚度曲线。CA⁃TIA中计算的悬架线刚度与实车测试的线刚度对比如图6所示，由图中可以看出，两者的结果比较吻合，其相对误差的均方根值为只有0.07%，说明在CAD软件中进行运动学仿真计算悬架线刚度是可行的。可以替代试验结果用于验证动力学模型的正确性。

4 动力学模型验证

下文基于ADAMS动力学软件，通过计算双横臂扭杆弹簧独立悬架的线刚度来验证动力学模型的正确性。

在ADAMS/Car模块中，默认假设前悬架关于整车纵向中心对称面对称，由此只需要建立半个前悬架左侧模型，另一半前悬架右侧模型的构件硬点坐标、几何构件、运动约束会自动生成。在建立双横臂悬架时对模型做如下简化[9]: 假定前悬架为一个多刚体系统，所有零部件都被认为是刚体，忽略导向杆件的柔性和变形。轮胎简化为刚性体，忽略各运动副内的摩擦力。前悬架左侧硬点坐标值见表1。

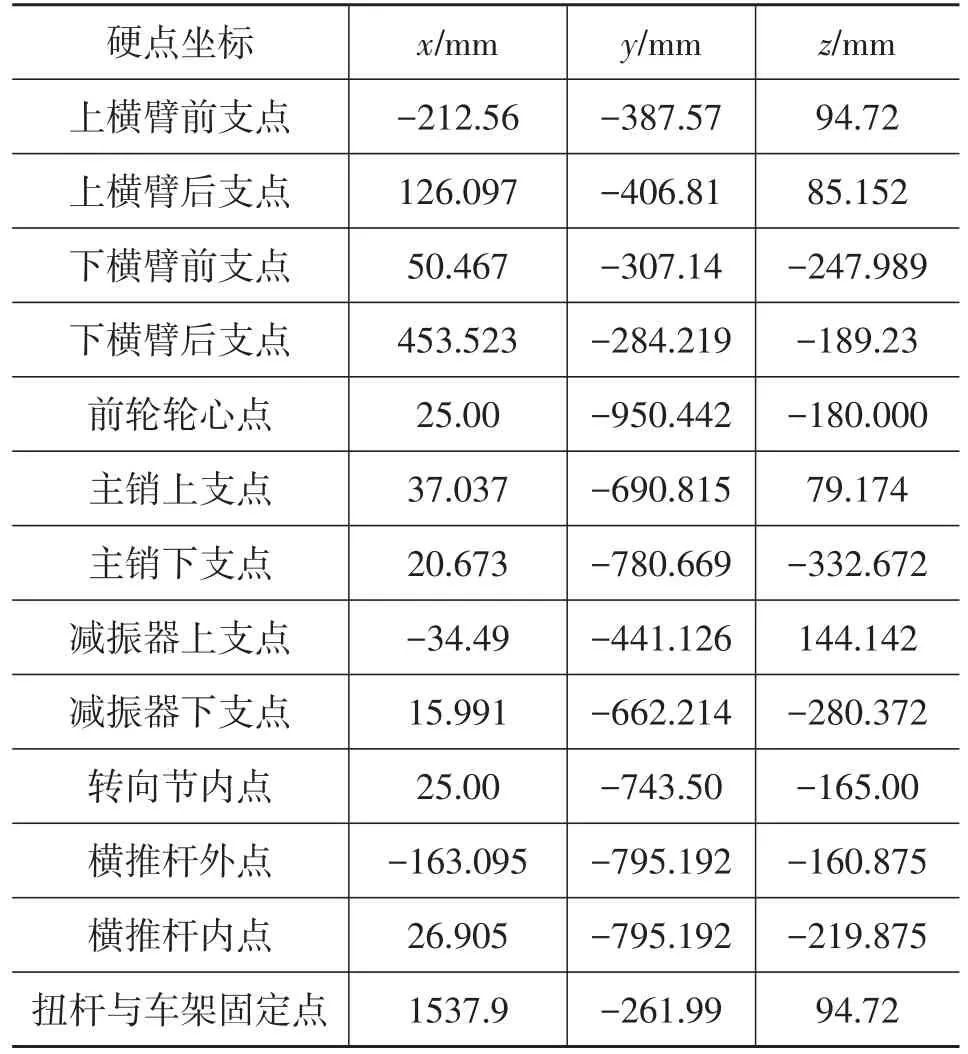
表1 悬架左侧硬点坐标值

整个悬架系统由上下横臂、转向节、主销、扭杆、转向横拉杆、减震器、车轮和试验台组成。上下横臂与主销之间用球铰副约束，上下横臂与车架连接处，在其中间通过橡胶衬套与车架连接，主销与转向节用固定副约束，转向节与车轮之间用旋转副约束，扭杆弹簧一端与上横臂以固定在一起，另一端与车架固定在一起，在扭杆中间断开添加一个扭簧，同时在断开处添加一个旋转副约束断开的两个杆件，以此等效为扭杆弹簧[10]。整个悬架放置在激振台架上施加垂直方向的运动来计算各参数的变化规律。在ADAMS/Car界面建立的双横臂独立悬架动力学模型，如图7所示。

在ADAMS／Car环境中建好模型后，对悬架做双轮同向激振试验，设置仿真步数为100，车轮上下跳动范围为-60～60 mm，对系统悬架刚度随车轮跳动垂向位移的关系进行仿真分析。计算完毕后，经后处理模块(ADAMS/Post Processor)进行数据处理，得到悬架线刚度。

ADAMS计算结果与CATIA计算结果对比如图8所示。

由图8可以看出，两者的结果相差很小，其相对误差的均方根值只有0.15%，由此可以说明在AD⁃AMS/Car中建立的双横臂扭杆弹簧独立悬架的动力学模型是正确。

5 结束语

基于虚位移原理提出了一种在CAD软件中计算双横臂扭杆弹簧独立悬架线刚度的计算方法，并且以某轻型客车的双横臂扭杆弹簧独立悬架为例，在CATIA中验证了该方法的可行性。

通过比较ADAMS和CAD计算的双横臂扭杆弹簧独立悬架线刚度，验证了在ADAMS/Car中建立的悬架动力学模型的正确性。且该方法同样适用于其他类型的独立悬架。

1 Rakheja S.Boileau P.-É.Wang Z.Politis H.Performance Analysis of Suspension Seats Under High Magnitude Vibra⁃tion Excitations:Part 1:Model Development and Validation.Journal of Low Frequency Noise,Vibration and Active Con⁃trol,2003,22:225～252.

2 Daniel A.Mantaras,Pablo Luque,Carlos Vera.Develop⁃ment and validation of a three-dimensional kinematic mod⁃el for the McPherson steering and suspension mechanisms.Mechanism and Machine Theory,2004,39:603～619.

3 D Marzougui,M Zink,A Zaouk,C D Kan,N Bedewi.Devel⁃opment and validation of a vehicle suspension finite element model for use in crash simulations.International Journal of Crashworthiness,2004,9:565～576.

4 陈刚,陈树人,邵景世.基于ADAMS的喷杆喷雾机前悬架仿真与优化.农化研究,2014.

5 石峰.双横臂独立悬架系统的分析与设计.西安：长安大学,2008.

6 蒋国平,周孔亢.旅行车独特悬架系统的运动特性木.机械工程学报,2008（4）：217-221.

7 曾迥立.双横臂独立悬架线刚度的非图解法计算[J].汽车工程,2006（8）:747-749.

8 席思文.基于CATIA的麦弗逊悬架运动仿真分析[J].机械设计与制造,2013（7）：114-116.

9 于海波,李幼德,门玉琢,邓阳庆.双横臂独立ADAMS建模及运动特性分析.汽车技术,2007（3）,5-8.

10 桑璟如.基于ADAMS多体动力学软件的轻型客车平顺性仿真.武汉：华中科技大学,2005.

（责任编辑帘 青）

修改稿收到日期为2014年3月1日。

5 橡胶复合悬架试验验证

由于橡胶副簧刚度受温度影响极易引起工作点漂移，需要进行常温和低温的疲劳台架试验，更需要进行用户环境(高低温及泥沙等)试验来评价对寿命的影响。表3的试验结果表明，该橡胶复合悬架满足用户可靠性要求。

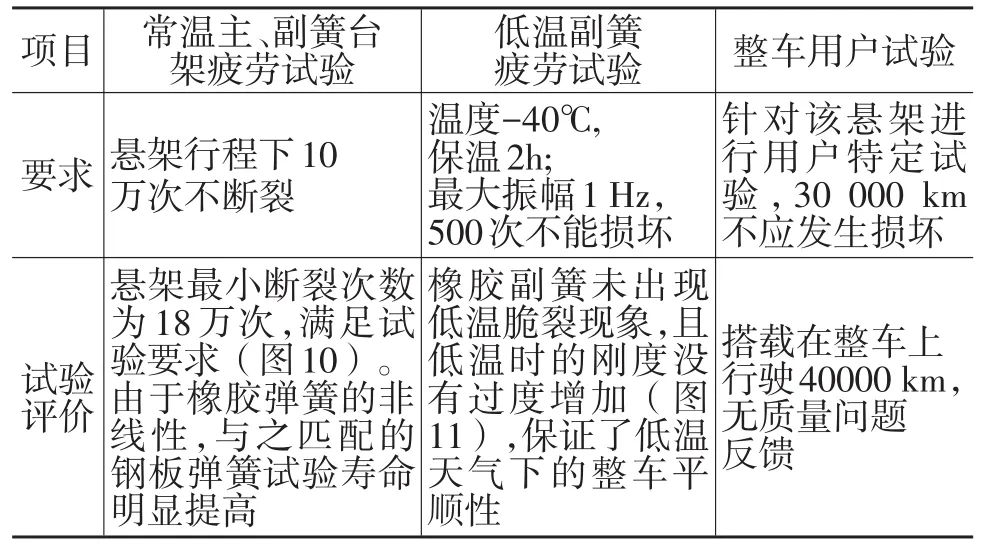
表3 台架和整车专项可靠性道路验证

5 结束语

通过设计橡胶复合悬架，使总成质量减轻20%、成本降低5%；同时由于橡胶弹簧的非线性特点，使与之匹配的钢板弹簧试验寿命得到明显提高。试验验证表明，该种复合悬架设计合理有效，推动了悬架系统的轻量化设计进程。

参考文献

1 刘惟信.汽车设计.清华大学出版社.2001.

2 Aeon Products Ltd.Aeon hollow rubber springs suspension kit for Land Rovers.Hermen Vlothuizen，1967.

3 王霄锋.汽车底盘设计.北京：清华大学出版社，2010.

4 卜继玲，钟汉文，等.系统仿真技术在橡胶悬架研发中的应用.汽车工程学报，2012（1）:51～54

5 周炜，黄友剑，等.单桥复合悬架橡胶空心弹簧刚度分析和参数优化.汽车技术，2011（10）:53～56.

(责任编辑帘 青)

修改稿收到日期为2014年11月1日。

A New Validation Method of Double Wishbone Independent Suspension Dynamics Model

Gong Haiqing,Yang Qiliang,Hu Li,Yuan Shuang
（Wuhan University of Science and Technology）

The liner stiffness of a light bus is calculated by CATIA 3D design mathematical model of motion simulation,and is compared with the test results,which verifies the correctness of the motion simulation results.The dynamic model of double wishbone torsion bar spring independent suspension is built in ADAMS/Car,and the liner stiffness is calculated by dynamic simulation.The comparison with the liner stiffness calculation results of motion simulation on CATIA proves correctness of the dynamic model.This method also applies to dynamic model validation of other type’s independent suspensions.

Dynamic model,Double wishbone independent suspension,Suspension liner stiffness,ADAMS,CATIA

动力学模型 双横臂独立悬架 悬架线刚度 ADAMS CATIA

U463.33

A

1000-3703（2015）02-0020-04

国家自然科学基金（汽车车身薄壁件颗粒阻尼复合结构振动—声学特性分析与优化 编号：51105283）资助。