新型混联式ISD悬架建模与参数优化*
聂佳梅 张孝良 孙晓强 陈龙
(江苏大学)
新型混联式ISD悬架建模与参数优化*
聂佳梅 张孝良 孙晓强 陈龙
(江苏大学)
提出了一种包含惯容器的新型混联式ISD悬架,该悬架由主弹簧、副弹簧、减振器和惯容器4个基本元件构成。建立了整车8自由度动力学数学模型,确定了悬架参数的优化范围及约束条件,采用粒子群算法进行悬架参数优化。结果表明,该优化方法可使座椅处垂向加权加速度均方根值降低26%,车辆行驶平顺性显著提高。
1 前言
惯容器能够有效改善隔振系统的隔振性能[1],2007年,江苏大学在国内开展了基于惯容器的车辆悬架性能提升研究,对惯容器结构设计、性能模拟以及ISD悬架结构形式确定等进行了分析[2,3]。
本文提出一种混联式惯容器-弹簧-阻尼器(In⁃erter-Spring-Damper,ISD)悬架,该悬架由2个弹簧(主弹簧、副弹簧)、1个减振器和1个惯容器等4个基本隔振元件构成。为确定该新型悬架的结构参数,根据车辆垂向动力学理论,建立了整车8自由度动力学数学模型,确定了悬架参数的优化范围及约束条件,并采用粒子群算法进行悬架参数优化。
2 惯容器工作原理
惯容器的动力学性质可描述为施加于惯容器两端点间的轴向作用力与其两端点间相对加速度成正比。惯容器的理想动力学方程可用下式表示:
式中,F为惯容器两端点间轴向作用力;v1、v2分别为惯容器两端点轴向移动速度;b为惯容器的惯质系数。
目前,惯容器的机械实现形式主要有齿轮齿条式惯容器和滚珠丝杠式惯容器两种,二者都是通过将惯容器两端点间直线运动转换为飞轮的旋转运动,从而实现飞轮惯性质量的放大和封装。以滚珠丝杠式惯容器为例,进一步分析惯容器的工作原理。滚珠丝杠式惯容器的动力学方程为[4]:
式中,v为惯容器两端点间相对运动速度;P为滚珠丝杠副的导程;ω为丝杠旋转角速度;J为飞轮转动惯量;T为丝杠驱动力矩;m为飞轮质量;r为飞轮半径;F为惯容器两端点间轴向作用力。
由式(2)可得惯容器两端点间轴向作用力F的具体表达式为:
结合式(1)和式(3)得到惯质系数b的表达式如下:
可以看出,通过改变滚珠丝杠副的导程、飞轮质量和半径便可实现惯质系数的调整,从而便于惯容器在工程上的灵活应用。
3 混联式ISD悬架建模
3.1 混联式ISD悬架布置形式
所提出的混联式ISD悬架由4个基本隔振元件构成,其具体布置形式如图1所示。
由图1可以看出,该布置形式仅在传统被动悬架基础上增加1个弹簧和1个惯容器,便于工程上直接实现,具有较高的应用价值。
3.2 整车动力学建模
根据牛顿第二运动定律,以车身静平衡位置为坐标原点建立车辆运动的数学模型。
当车身俯仰角和侧倾角均较小时,有如下近似几何关系[5]:
式中,za为车身质心处垂直位移;z10、z20、z30及z40分别为车身四角处垂直位移;zs0为座椅与车身接触点处的垂直位移;d1为左右轮距d的1/2;lf为前轴至质心距离;lr为后轴至质心距离;ls为座椅与车身接触点至质心距离;ds为座椅与车身接触点至车身纵向轴线的距离;φ和θ分别为车身俯仰角和侧倾角。
进一步可得座椅垂向运动方程为:
式中,k为座椅弹簧刚度;c为座椅阻尼系数;m为人体质量;zs为人体垂直位移。
车身垂向、俯仰及侧倾运动方程分别为:
式中,F1、F2、F3及F4分别为悬架四角处垂向作用力;Iφ为车身俯仰转动惯量;Iθ为车身侧倾转动惯量。
非簧载质量垂向运动方程如下:
式中,m1、m2、m3、m4分别为前后左右4个非簧载质量;q1、q2、q3及q4分别为前后左右4轮处路面垂直不平度输入;z1、z2、z3和z4分别为相应的非簧载质量垂直位移;kt为轮胎刚度。
根据混联式ISD悬架布置形式,可得悬架垂向作用力分别为:
式中,k1f、k2f为混联式ISD悬架前悬主弹簧刚度系数和副弹簧刚度系数;cf和bf为前悬阻尼系数和惯质系数;k1r、k2r、cr和br分别为相应的后悬参数;zn1和zn3分别为混联式ISD悬架级间垂直位移。
基于上述动力学方程,利用Matlab软件建立混联式ISD悬架整车8自由度仿真模型如图2所示。
4 悬架参数优化
4.1 优化目标及约束条件
《汽车平顺性随机输入行驶试验方法》中明确指出,评价车辆平顺性主要考虑座椅表面纵向、侧向及垂向3个轴向加速度。由于所建仿真模型只能计算座椅处垂向加速度,因此,这里不考虑座椅纵向及侧向加速度。优化目标函数确定为座椅处垂向加权加速度均方根值aw。目标函数值越小,车辆行驶平顺性越好,即优化目标为[6]:
aw的具体计算方法如下:
式中,Ga(f)为座椅处垂向振动加速度历程;为经频谱分析得到的功率谱密度;W(f)为频率加权函数,且与具体振动频率间存在如下关系:
若仅以振动加速度作为优化目标,优化结果可能会导致悬架动行程和车轮动载荷过大。因此,为保证车辆在行驶过程中的安全性以及控制撞击悬架限位概率,在优化过程中对车轮动载荷和悬架动行程设定如下约束条件。
a.车轮动载荷:根据正态分布概率积分表可知,当车辆动载荷均方根值σFd不超过静载荷G的1/3时,车轮跳离地面的概率不会超过0.15%,因此,设定约束条件为σFd≤G/3,其中,所研究车辆的静载荷G设定为3 450 N。
b.悬架动行程:当悬架动行程fd有效值σfd不超过限位行程[fd]的1/3时,悬架动行程在99.7%的时间域内可保持在合理范围,因此,设定悬架动行程的约束条件为σfd≤[fd]/3。一般乘用车[fd]为7~9 cm,本文选取[fd]为8 cm。
同时,为防止优化后得到的参数不符合悬架部件实际特性,设定了相关参数的优化范围如下:
4.2 参数优化
结合悬架参数的优化目标、约束条件及参数优化的实际要求,采用粒子群算法(PSO)进行混联式ISD悬架参数优化,参数优化的具体流程如图3所示。
5 性能分析
根据图3所示的优化流程,设置相关优化初始参数如下:种群规模100,粒子维数8,最大迭代次数200,初始惯性权重ω=0.53,加速因子r1=r2=1.18,适应度要求设定为0.2。经优化后得到的悬架参数如表1所示。
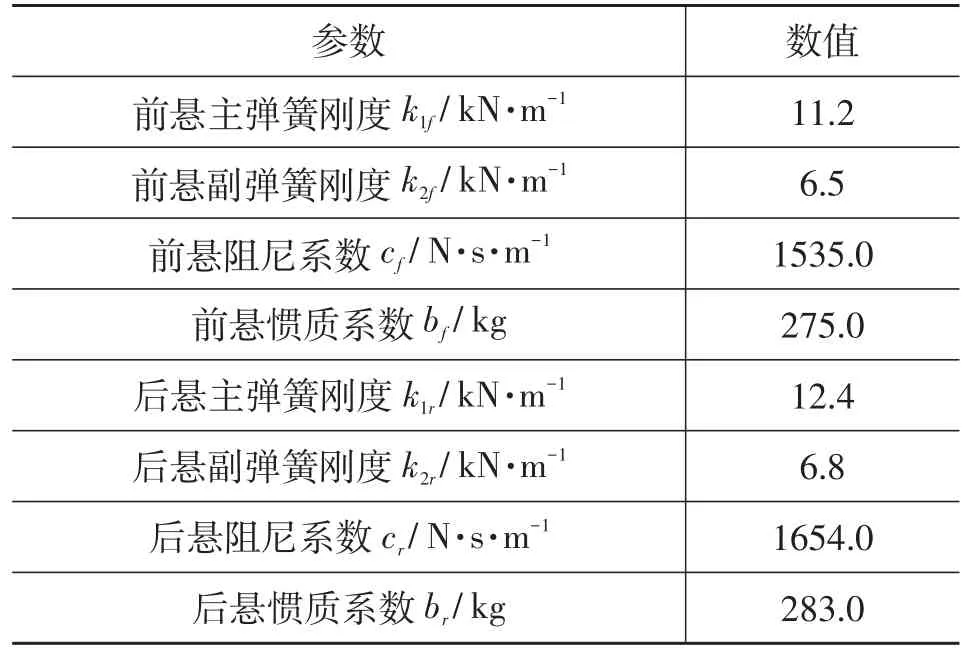
表1 ISD悬架最优参数
为验证参数优化的实际效果,以文献[4]给出的车辆参数为基础,对优化前、后悬架系统的主要性能指标进行仿真对比,其中座椅悬架的参数为弹簧刚度1 036 N/m,阻尼系数320N·s/m。假设车辆以90 km/h的速度行驶在C级路面上,仿真对比结果如图4~图6所示。
从图4中可以看出,优化后的座椅处垂向振动加速度比优化前小,经计算可得优化前、后座椅处垂向加权加速度均方根值分别为0.734和0.543,降幅达26%,车辆乘坐舒适性得到了大幅度改善。同时,由图5和图6可知,优化后的车轮动载荷和悬架动行程均有所增大,但经计算,二者仍满足车辆行驶安全性和控制撞击悬架限位概率的要求。
6 结束语
提出一种包含惯容器的车辆混联式ISD悬架结构,给出其具体布置形式,并采用粒子群优化算法对该新型悬架参数进行优化。优化后,在保证车辆行驶安全性和控制撞击悬架限位概率要求的同时,座椅处垂直振动加权加速度均方根值降低了26%,车辆乘坐舒适性得到了明显改善,表明所提出的ISD悬架结构及其参数确定方法准确有效。
1 Smith M C.Synthesis of mechanical networks:The inerter.IEEE Transactions on Automatic Control,2002,47(10):1648~1662.
2 陈龙,张孝良,聂佳梅,等.基于半车模型的两级串联型ISD悬架性能分析.机械工程学报,2012,48(6):102~108.
3 陈龙,杨晓峰,汪若尘,等.改进的ISD三元件车辆被动悬架性能的研究.汽车工程,2014,36(3):340~345.
4 孙晓强,陈龙,汪少华,等.非线性惯容器-弹簧-阻尼悬架系统隔振性能分析.农业工程学报,2013,29(23):38~45.
5 倪晋尚.汽车悬架的平顺性优化及仿真试验分析:[学位论文].南京:南京航空航天大学,2006.
6 孙晓强,陈龙,汪少华,等.2级串联式ISD悬架非线性建模与参数优化.农业机械学报,2014,45(6):7~13.
7 汪若尘,陈龙,张孝良,等.车辆半主动空气悬架系统设计与试验.农业机械学报,2012,43(4):6~10.
8 Michael Z.Q.Chen,Hu Yinlong,Huang Lixi,et al.Influ⁃ence of inerter on natural frequencies of vibration systems.Journal of Sound and Vibration,2014,333(1):1874~1887.
(责任编辑帘 青)
修改稿收到日期为2014年12月1日。
Modeling and Parameter Optimization of a New Type Hybridconnected ISD Suspension
Nie Jiamei,Zhang Xiaoliang,Sun Xiaoqiang,Chen long
(Jiangsu University)
In this paper,a new type hybrid-connected ISD suspension consisting of four basic components.i.e.main spring,auxiliary spring,damper and inerter is proposed.A vehicle dynamics mathematical model with eight-DOF is established and the suspension parameters optimization range and constraints are determined.The particle swarm optimization(PSO)algorithm is chosen for optimization of the suspension parameters,the results indicate that the root mean square value of weighted seat vertical acceleration goes down by 26%,thus the vehicle ride comfort is improved considerably.
Suspension,Inerter,Vehicle model,Parameter optimization
悬架 惯容器 整车模型 参数优化
U463.33
A
1000-3703(2015)02-0044-04
江苏省科技支撑计划(工业)资助项目(BE2013096);江苏省自然科学基金资助项目(BK20130521)。

