基于车辆平顺性分析的橡胶衬套动态特性建模
秦民 蒋永峰 宋雨
(中国第一汽车股份有限公司技术中心 汽车振动噪声与安全控制综合技术国家重点实验室)
基于车辆平顺性分析的橡胶衬套动态特性建模
秦民 蒋永峰 宋雨
(中国第一汽车股份有限公司技术中心 汽车振动噪声与安全控制综合技术国家重点实验室)
橡胶衬套的动态特性与载荷的激振频率、幅值等因素相关,其模型的准确性影响车辆平顺性的仿真精度。建立了包含材料弹性、粘弹性与弹塑性的橡胶衬套动态模型,分别采用多项式、分数导数与Bouc-wen模型描述橡胶衬套的弹性、频率相关性及振幅相关性。通过参数辨识确定衬套模型参数并进行仿真,验证了所建模型的准确性。
1 前言
Kelvin-Voigt模型由一个弹簧单元和一个阻尼单元并联而成,广泛应用于ADAMS等商业软件中[1~3]。Maxwell模型由弹簧单元和阻尼单元串联而成,多应用于当前商业有限元软件的粘弹性计算分析中[4,5]。SJO¨BERG等采用基于分数导数的粘弹性模型,可以在较宽频率范围内描述衬套的频率相关性[6,10]。此外,描述衬套振幅相关性的模型主要包括库伦摩擦模型、平滑摩擦模型与Bouc-wen摩擦模型等[11,15]。分数导数模型能够准确描述橡胶衬套的粘弹性特性,Bouc-wen模型能够描述橡胶衬套复杂摩擦特性曲线的现状[6,11~13]。
本文建立了集成静刚度弹性单元、分数导数粘弹性单元与Bouc-wen弹塑性单元的橡胶衬套动态模型,通过参数辨识获得模型参数并进行了仿真分析。结果表明,本文动态模型较好描述了衬套特性的频率相关性与振幅相关性,可以较好的预测其动态性能,可用于车辆平顺性仿真的精确计算。
2 橡胶衬套动态特性建模
2.1 常用橡胶衬套模型
图1为常用的2种衬套模型,模型滞后角曲线如图2所示。
对比图3中橡胶衬套试验滞后角曲线形状,图2中Kelvin-Voigt模型在低频段(3 Hz以下)时阻尼滞后角偏小,而高频段(大于10 Hz)时阻尼滞后角远大于试验值;同样,3参数Maxwell模型在低频段(3 Hz以下)时阻尼滞后角偏小。
2.2 分数导数-Bouc模型
本文建立的橡胶衬套动态特性模型包含弹性单元、粘弹性单元与弹塑性摩擦单元,如图4所示。橡胶衬套动态特性力—位移关系如下:
a.弹性力模型
采用多项式描述橡胶衬套的弹性力如下式:
b.粘弹性模型
采用分数导数模型能在较宽频率范围内描述衬套的频率相关性,且模型参数较少,其力与位移关系可以表达为:
分数导数Dαx最常用的定义由Riemann-Liouville积分给出[6]:
式中,Γ为gamma函数,即:
André Schmidt[16]讨论了分数导数的数值计算方法,表达式如下:
c.弹塑性摩擦模型
Bouc-wen模型能够对非线性系统进行准确描述,相比于平滑摩擦模型,其可以描述更复杂的橡胶衬套摩擦迟滞特性,模型表示为:
通过改变模型参数值,可以描述复杂的非线性摩擦特性,图4为当参数b、n取不同值时bouc-wen模型的摩擦迟滞曲线。
2.3 模型参数辨识及结果对比
模型中共包含9个待辨识参数,通过参数优化,使得橡胶衬套的试验与仿真动刚度及滞后角误差函数值最小:
式中,m为辨识工况的数量;分别为仿真与试验动刚度值;分别为仿真与试验滞后角值。
采用序列二次规划法(NLPQL)对橡胶衬套参数进行分步辨识。
第1步:采用多项式拟合衬套静刚度试验数据,确定参数k1、k2。
第2步:当激励频率很低时,橡胶衬套变形速度非常小,此时橡胶的粘弹性效应可以忽略,根据橡胶衬套在低频率、多个位移激励幅值下动刚度与滞后角试验数据,确定Bounc-wen模型中的5个参数。
第3步:对表征橡胶衬套粘弹性特性的分数导数模型参数辨识,根据某幅值、多个频率下动刚度与滞后角试验数据,在消除摩擦效应对粘弹性特性影响的基础上确定参数。
第4步:在初步确定9个参数的基础上,根据多幅值、多频率的衬套试验动刚度与滞后角数据,对所有参数进行进一步优化,确定误差最小的模型参数值。结果如表1所示。

表1 模型辨识参数
图5为橡胶衬套试验与仿真的动刚度、滞后角数据对比曲线,可知在不同激励频率与幅值条件下,动刚度最大误差在5%以内,阻尼滞后角最大误差在10%以内。
图6为相同幅值、不同频率激励下的试验与仿真信号对比,图7为相同频率、不同幅值激励下的试验与仿真信号对比,可知仿真与试验曲线误差都比较小。
综合图5~图7可知,频域和时域的仿真与试验数据对比中,新建立的分数导数-Bouc模型仿真结果与橡胶衬套试验数据误差比较小,较好地模拟了橡胶衬套的频率相关性与振幅相关性。
3 应用实例
图8是一个橡胶衬套单自由度隔振系统,衬套模型分别为分数导数-Bouc模型与Kelvin-Voigt模型。两种衬套模型参数由相同试验数据辨识得到。
系统的运动方程分别为:
式中,Δx=x-z。
取不同系统质量m1=15m2,经过计算,系统固有频率分别为1.6 Hz与7.2 Hz。给系统施加单位阶跃激励,从图9可以看出,当系统固有频率为1.6 Hz时,Kelvin-Voigt模型隔振系统衰减时间较长,说明模型在低频时的阻尼滞后角偏小;当系统固有频率为7.2Hz时,Kelvin-Voigt模型隔振系统衰减时间较短,说明模型在高频时的阻尼滞后角偏大。所得结果进一步验证了图2中的结论。
4 结束语
给出了描述衬套频率及振幅相关性的衬套动态模型,根据试验数据进行模型参数辨识,并进行了仿真分析对比,
a.验证了Kelvin-Voigt模型在低频段与高频段分别过低和过高估计了衬套的阻尼因子,不适合用于车辆平顺性分析。
b.提出的分数导数-Bouc动刚度小于5%、滞后角误差小于10%,时域仿真数据与试验数据重合度较高,满足平顺性精确仿真要求。
c.实际车辆行驶工况复杂,包含很多冲击工况,文中用稳态试验数据辨识的衬套动态模型对冲击工况的仿真精度还有待进一步验证。
1 于增亮,张立军,余卓平.橡胶衬套力学特性半经验参数化模型.机械工程学报,2010,46(14):115~123.
2 Ya P,Hartono S.Modeling of nonlinear elastomeric mounts.Part 1:Dynamic testing and parameter identification.SAE Technical Paper Serials 2001-01-0042,2001.
3 Park S W.Analytical modeling of viscoelastic dampers for structural and vibration control.Solids and Structures, 2001,38:8065 8092.
4 M.Nonlinear isolator dynamics at finite deformations:an ef⁃fective hyperelastic,fractional derivative,generalized fric⁃tion model.Nonlinear Dynamics,2003,33:323~336.
5 Gil-Negretea N,Vinllasa J,Kari L.A simplified methodolo⁃gy to predict the dynamic stiffness of carbon-black filled rubber isolators using a finite element code.Journal of Sound and Vibration,2006,296:757~776.
6 M,KARI L.Non-linear behavior of a rubber isolator system using fractional derivatives.Vehicle System Dynamics,2002(37):217~236.
7 Pritz T.Five-parameter fractional derivative model for poly⁃meric damping materials.Journal of Sound and Vibration, 2003,265:935~952.
8 Pritz T.Analysis of four-parameters fractional derivative model of real solid materials.Journal of Sound and Vibra⁃tion,1996,195(1):103~115.
9 Schmidt A,Gaul L.Finite element formulation of viscoelas⁃ tic constitutive equations using fractional time derivatives.Nonlinear Dynamics,2002,29:37~55.
10 吴杰,上官文斌.采用粘弹性分数导数模型的橡胶隔振器动态特性的建模方法.工程力学,2008,25(1): 161~167.
11 于增亮,张立军,罗鹰.橡胶衬套力学特性半经验参数化模型.机械工程学报,2010,46(14):115~123.
12 王娜.面向汽车耐久性分析的底盘橡胶衬套建模研究:[学位论文].长春:吉林大学,2011.
13 潘孝勇.橡胶隔振器动态特性计算与建模方法的研究:[学位论文].浙江:浙江工业大学,2009.
14 Jacco Koppenaal,Jan Van Oosten.General Modeling of Nonlinear Isolators for Vehicle Ride Studies.SAE Interna⁃tional,2010-01-0950.
15 SJ BERG M.Rubber isolators-measurements and mod⁃elling using fractional derivatives and friction.SAE,2000-01-3518,2000.
16 Schmidt A,Gaul L.Finite element formulation of viscoelas⁃tic constitutive equations using fractional time derivative.Nonlinear Dynamics,2002,29:37~55.
(责任编辑帘 青)
修改稿收到日期为2014年12月1日。
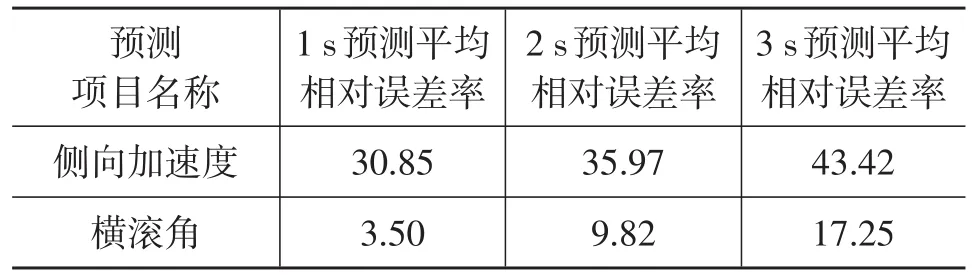
表3 预测方法的平均相对误差 %
由表3可知,在短期的预测时间内(约1 s),所建立的时间序列模型具有很好的预测效果,基本满足汽车实时预测系统对预测精度的要求,充分说明此预测系统的可行性。
6 结束语
进行了基于ARM和Android系统的移动终端车载数据采集与状态预测的研究,阐述了预测系统的硬件组成和软件设计方法,并通过实车道路试验验证了该预测系统的可行性。该预测系统不仅提高了安卓车载终端对汽车主动安全的融合性,而且与传统车载终端相比,有效降低了汽车状态数据采集成本并具有良好的可扩展性和灵活性。
参考文献
1 BilimoriaKD,Wie B.Time-Optimal Three-Axis Reorien⁃ taion of a Rigid Spacecraft.Journal of Guidance,Control, and Dynamics(S0731-5090),1993,16(3):446~452.
2 刘付强.基于MEMS器件的捷联姿态测量系统技术研究:[学位论文].哈尔滨:哈尔滨工程大学.2007.
3 夏安邦.系统建模理论与方法.北京:机械工业出版社,2008.
4 杨叔子,吴雅,轩建平,等.时间序列分析的工程应用.武汉:华中科技大学出版社,2007.
5 王秀峰,卢桂章.系统建模与辨识.北京:电子工业出版社,2004.
6 张荣辉,贾宏光,陈涛,等.基于四元数法的捷联式惯性导航系统的姿态解算.光学精密工程,2008(10):1963~1970.
7 王佳顼.基于Android的电子词典手机客户端的设计与实现:[学位论文].北京:北京交通大学,2012.
8 米勒.蓝牙核心技术:全球无线通信开放规范的权威性指南.北京:机械工业出社,2001.
9 GB/T6323.1—94汽车操纵稳定性试验方法蛇行试验.
10 GB/T6323.6—94汽车操纵稳定性试验方法稳态回转试验.
(责任编辑文 辑)
修改稿收到日期为2014年11月24日。
Dynamic Characteristics Modeling of Rubber Bushing for Vehicle Ride Analysis
Qin Min,Jiang Yongfeng,Song Yu
(State Key Laboratory of Comprehensive Technology on Automobile Vibration and Noise&Safety Control,China FAW Co.,Ltd R&D Center)
The dynamic properties of rubber bushing are correlated to exciting frequency and amplitude of loads, its modeling accuracy directly affects the vehicle ride simulation precision.In this research,the dynamic model including material elasticity,viscoelastic and elastic-plastic of rubber bushing is established.We use polynomial,fractional derivative and Bouc-wen model to describe the dependency of elasticity,frequency and amplitude of rubber bushing.With parameter identification and simulation of rubber bushing,the accuracy of the model is verified.
Rubber bushing,Dynamic characteristics,Ride analysis,Modeling
橡胶衬套 动态特性 平顺性分析 模型
U461.4
A
1000-3703(2015)02-0034-05

