基于模态试验和有限元模态分析的转向盘怠速抖动改进
卢元燕 苏世荣
(江淮汽车股份有限公司)
基于模态试验和有限元模态分析的转向盘怠速抖动改进
卢元燕 苏世荣
(江淮汽车股份有限公司)
针对某车型怠速工况下转向盘抖动问题,对整车进行了怠速振动试验并对转向盘进行了模态试验,确认转向盘系统与仪表板横梁及横梁与车身连接处的连接刚度不足导致整个转向系统模态下降,从而引起了共振。针对该问题建立了转向系统有限元模型,并根据模态试验结果对模型进行了验证。在该模型基础上对上述连接刚度进行了优化,对优化方案进行试验验证的结果表明该方案有效。
针对某款轿车怠速工作状态下转向盘振动过大问题,先通过模态试验方法对其原因进行了快速识别,然后通过有限元分析方法对该问题进行了分析和改进,试验和仿真的有效结合较好地解决了该转向盘抖动问题。
1 怠速转向盘抖动原因分析
为了客观评价该转向盘的抖动情况,针对怠速开、关空调工况对转向盘进行了振动加速度怠速振动测试,传感器布置在转向盘12点位置,如图1所示。试验测得转向盘的振动频谱数据如图2和图3所示,由图2和图3可知,关空调工况下影响转向盘抖动的主要频率为25 Hz左右,开空调工况下影响转向盘抖动的主要频率为26 Hz左右。
根据企业标准,基于整车坐标系,要求怠速关空调时乘用车转向盘三向加速度均小于0.03g,怠速开空调时乘用车转向盘三向加速度均小于0.05g。由表1中的数据可以看出,该车型怠速工况下转向盘X向和Z向的加速度值均较大,在开空调时振动更为明显。

表1 转向盘的加速度值g
为了分析怠速工况下转向盘抖动原因,使用锤击法对转向系统进行了模态测试。试验测得的转向系统1阶垂向(X、Z向)频率为24.97 Hz,1阶横向(Y向)频率为25.02 Hz,对应的整体振型分别如图4和图5所示。
通常情况下,直列四缸发动机怠速工况下的激振主要是2阶往复惯性力,其频率与车辆搭载的发动机转速有关。发动机怠速时的2阶激励频率公式为[1~5]:
式中,fE为发动机怠速时的2阶激励频率;n为发动机转速。
根据公式(1)可以计算出该车型直列四缸四冲程发动机在开、关空调下的2阶激振频率如表2所示。

表2 发动机激振频率
由表2可以看出,该车型怠速时转向盘抖动主要是由于其转向系统固有频率(24.97 Hz)和发动机2阶激励频率(关空调25 Hz、开空调26.7 Hz)耦合,发生了共振。
怠速工况下影响转向盘抖动的主要因素是整个转向系统的模态。为了进一步分析原因,对转向盘和转向管柱系统进行台架试验,在12点位置布置三向传感器,力锤3点位置敲击Y向,力锤6点位置敲击X向。试验结果如图6所示,测得该子系统X、Z向固有频率为46.95 Hz,满足设计目标要求(≥40 Hz)。而该子系统安装到仪表板横梁上,再整体固定到车身后的固有频率下降为24.97 Hz。由此可以判定转向系统与仪表板横梁连接处以及仪表板横梁与车身连接处的约束刚度不足导致了整个转向系统模态的下降,最终导致共振,故加强连接处的刚度可解决转向盘抖动问题。
为了避免共振,一般要求转向系统的固有频率比发动机2阶激励频率高5~7 Hz,因此该车型整个转向系统的固有频率至少应为31.7 Hz。
2 转向系统模型的建立
采用有限元分析方法优化转向管柱和仪表板横梁的连接刚度[6,7]。根据整车状态建立了转向系统有限元模型如图7所示,模型中包含了转向盘本体、转向管柱、仪表板管梁和车体等部件。
初始状态下仿真计算结果为1阶垂向振动频率25.49 Hz,1阶横向振动频率为25.72 Hz,如图8和图9所示。表3对该系统振动频率的试验值与仿真值进行了对比,相对误差保持在3%以内,可见该有限元模型具有较好的可靠性和准确性,可以用于下一步的结构优化。

表3 试验与CAE模态计算结果对比
3 仪表台管梁改进及试验验证
原始管梁及安装结构如图10所示,转向盘及调整机构通过ABCD共4个螺栓固定在仪表台管梁上。仪表台管梁总成通过10个螺栓固定在车身上,分别为EFGHIJ共6个螺栓固定在前围钣金上,K(2个)和L(2个)共4个螺栓固定在地板上,如图11所示。
通过CAE仿真分析,找出整个子系统刚度薄弱位置如图12所示,并针对薄弱环节进行改进。改进方案主要包括改进连接处的结构、增加支架、加密焊点和加厚板件等,如图13所示。
GH连接处的钣金N主要约束仪表台管梁Z向运动,如图14左图所示,但原始结构刚度仍不足,未起到较好的作用。为了加强Z向的受力约束,对该处结构进行了更改,如图14右图所示。
AD两处固定点是仪表台管梁约束转向管柱的关键位置,如图15左图所示,通过仿真分析发现,此处的Z向振动较大,原因主要是GH位置和仪表台管梁本身在AD点对转向管柱的约束不足。为此将该处结构变为三角支架结构,使其能够更好的在Z方向约束转向管柱,如图15右图所示。
地板连接支架和管柱支架仅通过KL 4个焊点约束,在仿真分析时发现此处振幅较大,为此在左右两侧及与仪表管梁连接处增加二氧化碳保护焊,如图16所示。
管柱连接位置EF和IJ左右对称,车身钣金在X方向及绕Y轴旋转方向对仪表台管梁的约束不足,为此在钣金位置增加了L型支架,使得钣金变为盒装结构,同时厚度由1.8 mm变更为2.0 mm,以加强X及绕Y轴的约束,如图17所示。
基于原始分析模型,通过仿真对上述不同的改进方案进行了分析计算,仿真结果如表4所示。
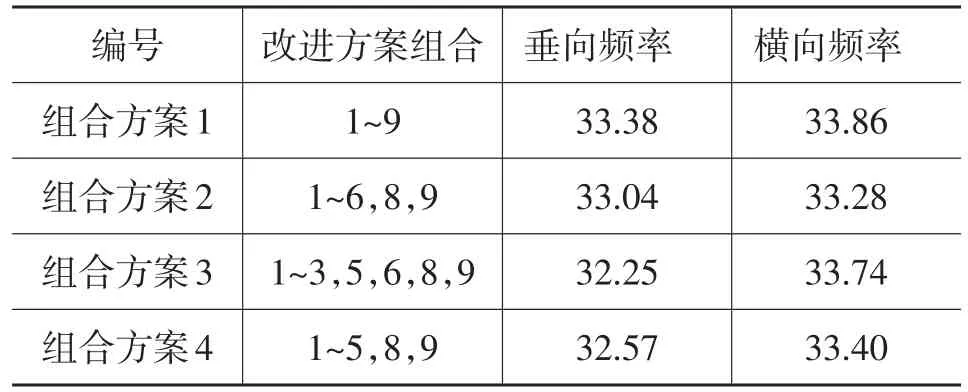
表4 仿真计算结果 Hz
由表4可以看出,4种方案都能满足上述确定的至少大于31.7 Hz的目标要求,综合考虑该车型改进中所涉及的模具更改及周期,最终决定采用方案4:8和9两处厚度由1.8 mm改为2.0 mm,横梁与转向管柱的固定结构等3处结构变更以及2处加焊。
为了验证方案4的有效性,对涉及到的部件进行了样件试制,通过模态试验对方案4进行了验证。改进车上试验测得的转向系统模态值为33.46 Hz,较好地达到了目标要求。对改进后的转向系统进行了怠速开关空调工况下转向盘的振动测试,振动频谱如图18和图19所示,可知各向加速度均符合目标要求,改进效果明显。
1 岳涛,朱卫宁.轿车转向系统优化设计.安徽电子信息职业技术学院学报,2012,5(11):48~51.
2 倪振华.振动力学.西安:西安交通大学出版社,1990: 35~37.
3 谯万成,张铭成,刘旌扬.基于模态分析的汽车转向盘怠速抖动优化.汽车技术,2011(11):27~30.
4 杨亮,吴行让,张硕,等.谭万军.汽车怠速转向盘振动控制研究.噪声与振动控制,2011(10):80~85.
5 赵洪辉.轿车转向盘振动分析与控制:【学位论文】.吉林:吉林大学,2006.
6 卢礼华,单峰,邹杰.基于有限元技术和试验模态的转向盘优化设计.合肥工业大学学报,2013,9(35): 1163~1167.
7 谢暴,陶其铭.基于模态分析的汽车转向盘怠速抖动改进研究.装备制造技术,2010,3:14~16.
8 庞剑,谌刚,何华.汽车噪声与振动-理论与应用.北京:北京理工大学出版社,2006.
9 王建文,胡伟,田子龙.SUV转向系统模态试验及优化.汽车工程师,2012(8):47~50.
(责任编辑帘 青)
修改稿收到日期为2014年11月1日。
Idle Vibration Improvement of Steering Wheel Based on Modal Test and Finite Element Analysis
Lu Yuanyan,Su Shirong
(Anhui Jianghuai Automotive Co.,Ltd)
To troubleshoot the cause of idle vibration of the steering wheel of a vehicle in idling,we make vehicle idling vibration test and steering wheel modal test,to determine that the resonance is caused by insufficient connection stiffness between instrument panel beam system and the steering wheel and the body that results in the decline of the entire steering system modal.To eliminate this problem,a finite element model of the steering system is created and validated according to the modal test results.The connection stiffness is optimized on the basis of the finite element model.The optimization proposal is tested,which demonstrates the effectiveness of this proposal.
Steering wheel,Idle vibration,Finite element modal analysis,Modal test
转向盘 怠速抖动 有限元模态分析 模态试验
U463.4
A
1000-3703(2015)02-0008-04

