随机需求下考虑质量控制的供应链协调模型

夏道明，汪峻萍，张 斌

(1.合肥幼儿师范高等专科学校基础部，安徽合肥 230011;2.合肥工业大学数学学院，安徽合肥 230009)

随机需求下考虑质量控制的供应链协调模型

夏道明1，2，汪峻萍2，张 斌2

(1.合肥幼儿师范高等专科学校基础部，安徽合肥 230011;2.合肥工业大学数学学院，安徽合肥 230009)

研究了随机市场条件下供应链中产品的质量控制问题，建立了需求依赖于制造商质量控制努力与零售商质量检验努力的供应链协调模型。分析了制造商质量控制努力与零售商质量检验努力对零售商订购量的影响，分别给出了分散决策和集中决策下制造商的最优的质量控制努力、零售商的最优质量检验努力及销售期的最优订购量，利用收益共享契约使供应链达到完美协调，并通过数值算例对模型进行了仿真计算。

随机需求;质量控制;利润共享契约;完美协调

近年来，随着经济全球化的浪潮，传统企业之间的竞争模式已经转换成供应链与供应链之间的竞争模式，而在供应链内各成员企业对质量行为的决策，合作与协调将决定着产品质量。在经济迅速发展的时代，消费者对产品质量的要求也越来越高，这就导致产品质量的好坏直接影响市场对该产品的需求［1-3］。这时，在供应链中的各成员为了扩大需求，收获更多的利润，他们将在产品的质量控制上付出更多的努力。而提高产品的质量不仅仅只依赖于制造商对产品的控制，还依赖于零售商对产品的检验，以此来保证了每个产品的质量。如制造商提供的产品质量水平越高，产品将会获得更高的美誉度，消费者对产品的需求自然会上升。同样的道理，在供应链中零售商对产品质量的检验努力也会起到相同的作用。相反，产品的需求变化也会影响着制造商和零售商对质量的选择。因此，在如今瞬间万变的市场竞争中，考虑对产品的质量控制显得格外重要。

迄今为止，针对供应链中的质量控制问题研究大致可以分为四类:第一类是供应链中只研究了供应商质量努力的影响，这类问题没有考虑零售商的质量检验努力的影响，如Balachandran［4］研究了制造商如何通过基于外部失败信息或基于检验过程的担保/惩罚合同来诱导供应商的质量选择;张翠华和鲁丽丽［5］研究了基于供应商检验和质量努力隐匿的协同质量控制，考虑了供应商质量努力、自身检验水平信息隐匿以及两者都隐匿时供应链的协同质量控制问题。第二类是供应链中考虑了质量控制问题，却没有建立具体的订购策略模型，如Baiman［6］研究了质量风险信息对供应链协调的影响;Tapiero［7］研究了供应链中考虑消费者风险对质量水平选择的博弈模型;刘强等［8］对供应链质量控制与协调研究作了全面的评析;第三类是在探讨质量控制问题上主要基于委托代理理论，鲜有运用回购契约，收益共享契约等来进行协调，如李丽君，黄小原和庄新田［9］研究了运用委托代理理论方法探讨了双边道德风险条件下供应链的质量控制策略;徐庆等［10］研究了零售商与供应商之间由于信息不对称引起的质量控制委托代理问题等;第四类是将上述三类研究进行了整合改进，但研究的还不够完善;如Gurnani［11］研究了市场需求会受到成员质量影响的供应链协调问题和胡军等［12］研究了线性需求条件下考虑质量控制的供应链协调契约模型，但均没有考虑市场的随机性;肖迪和潘可文［13］研究了在随机环境下考虑基于收益共享契约的供应链成员的质量控制问题，但没有综合考虑制造商和零售商同时对质量控制的影响。通过上述文献的分析比较，本文有两大特点，一是在随机环境下综合考虑了制造商和零售商的质量控制努力对市场需求的影响;二是运用了收益共享契约来实现了供应链的完美协调。

本文研究了随机市场条件下供应链中产品的质量控制问题，建立了需求依赖于制造商质量控制努力与零售商质量检验努力的供应链协调模型，分析了制造商质量控制努力与零售商质量检验努力对零售商订购量的影响，分别给出了分散决策和集中决策下制造商的最优的质量控制努力，零售商的最优质量检验努力及销售期的最优订购量，利用收益共享契约使供应链达到完美协调，并通过数值算例对模型进行了仿真计算。

1 记号与假定

1.1 符号说明

D:市场需求;

α:表示制造商和零售商都不做质量控制努力时所面临的市场需求;

Q:零售商的订购量;

p:零售商的零售价格;

e:零售商的质量检验努力;

γ:表示零售商的质量检验努力的变化对市场需求的影响;

v:销售季节结束后单位产品的残值;w:制造商的批发价格;c:制造商的产品成本;

θ:制造商的质量控制努力;

λ:表示制造商的质量控制努力的变化对市场需求的影响;

其中，用上标“c”或“d”表示集中决策系统和分散决策系统，用下标“m”、“r”或“s”表示制造商，零售商或供应链系统。

1.2 模型假定

考虑在随机市场下由一个制造商与一个零售商组成的两级供应链，零售商的需求受质量控制与检验努力的影响。借鉴胡军等线性需求条件下考虑质量控制的供应链协调契约模型中的市场需求函数，假定零售商所面临的需求函数为:

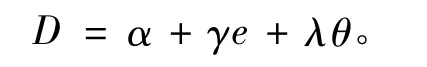
由于市场的不确定性，本文假定在整个销售期内的实际需求是D(e，θ)与均值为1的正随机变量ξ的乘积，随机变量ξ的分布函数与密度函数分别是F(x)和f(x)，这样零售商所面临实际需求为X(e，θ)=D(e，θ)ξ，其概率密度函数可表示为

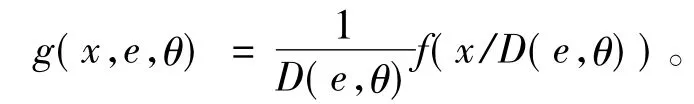
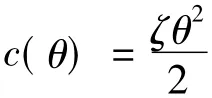
2 分散决策模型

在制造商占主导地位的Stackelberg博弈中，制造商先确定质量控制水平，在决定努力水平时会考虑零售商的反应。零售商在制造商确定的质量控制努力水平下，再决定订购量和质量检验努力水平。由此可建立模型如下:

零售商在整个销售期内的期望收益函数为

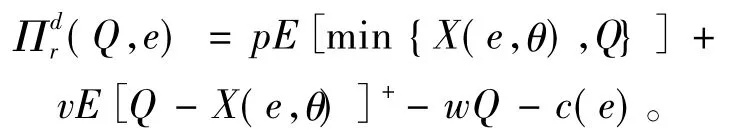
化简整理得

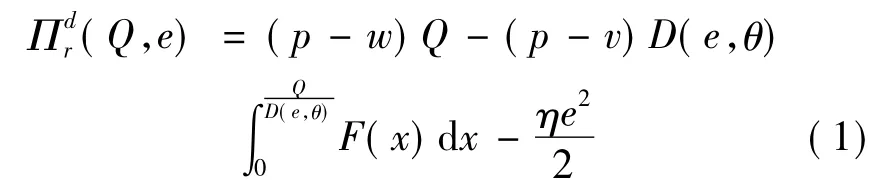
制造商在整个销售期内的期望收益函数为

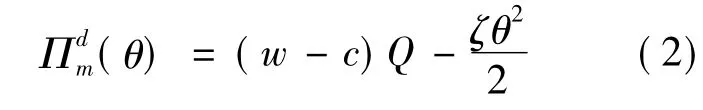
对(1)式中的Q求一阶偏导数和二阶偏导数，得

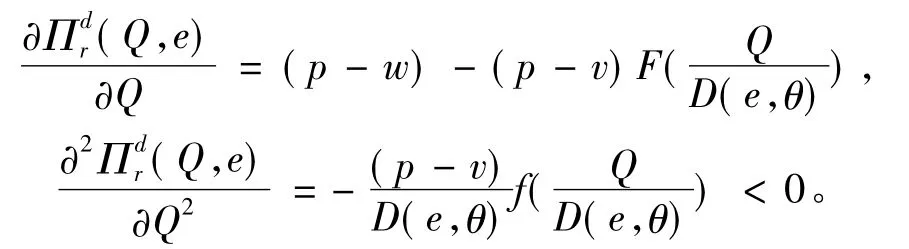
利用一阶的最优性知，Qd=ΦdD(e，θ)，其中

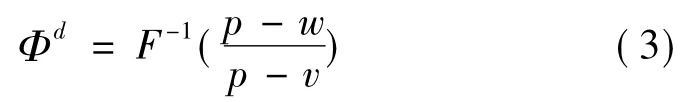
将(3)式代入(1)式，可得

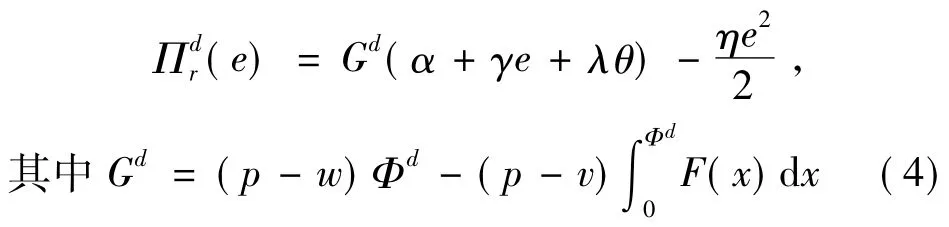
对(4)式中e求一阶导数和二阶导数得

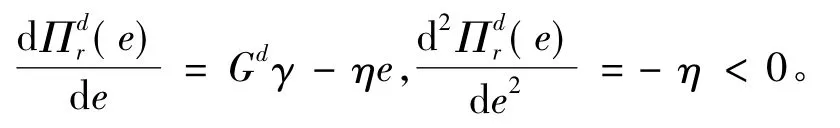
利用一阶导数的最优性知

将(5)代入(3)得

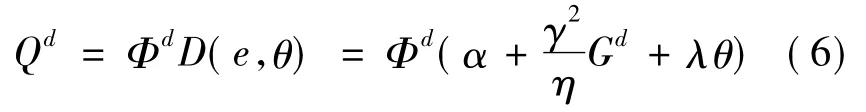
将(6)式代入(2)式知

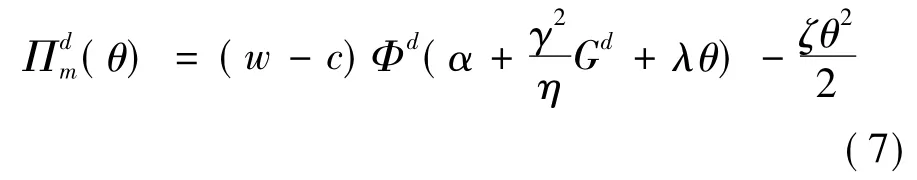
对(7)式中θ一阶导数和二阶导数得

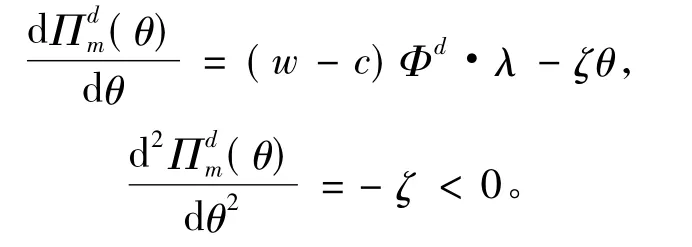
利用一阶最优性知，

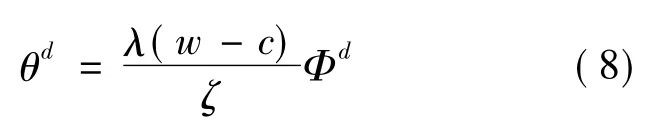
由(3)式和(8)式易得

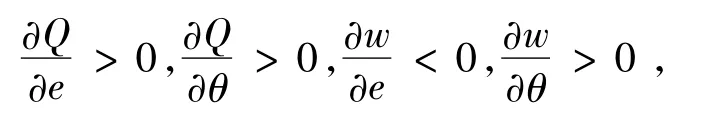
从而可得以下推论。

推论1在分散决策下:

(i)零售商的质量检验努力水平和制造商的质量控制努力水平越高，零售商的订购量就越大;

(ii)零售商的质量检验努力水平越高，制造商的批发价格就越低，相反，制造商的质量控制努力水平越高，制造商的批发价格也越高。

从推论1(i)说明了当制造商和零售商通过质量控制努力使产品的质量水平提高了，相应的市场需求自然会上升，因此，零售商的订购量就会增大。推论1(ii)说明了零售商的质量检验努力水平越高，相应的投入成本也就越高，此时，零售商就该享有较低的批发价，否则零售商将失去质量检验的动力，这样会影响整个供应链的利润;而制造商的质量控制水平越高，相应的投入成本也越高，这样制造商就提高批发价格来弥补自己投入的质量控制成本。

3 集中决策下模型

在集中决策下，制造商和零售商被看成是隶属于同一家公司，他们作为一个整体负责产品的制造和销售，并且统一做出决策来追求供应链系统的期望利润最大化，而不考虑他们各自的利润分配。因此，在集中决策下，供应链系统的期望收益函数为

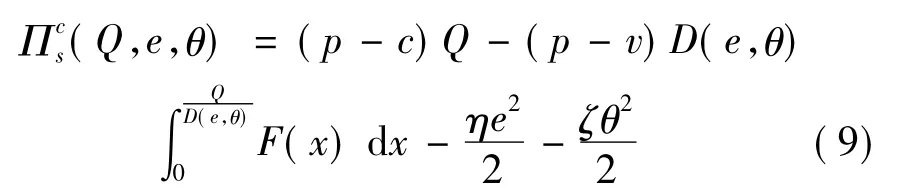
对(9)式中的Q求一阶偏导数和二阶偏导数，得

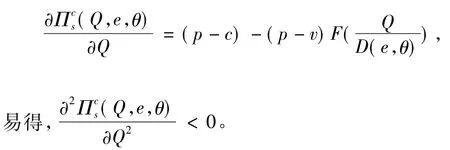
利用一阶导数的最优性知，Qc=ΦcD(e，θ)，其中

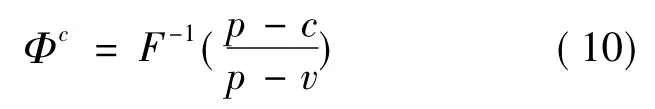
将(10)代入(9)式可得，

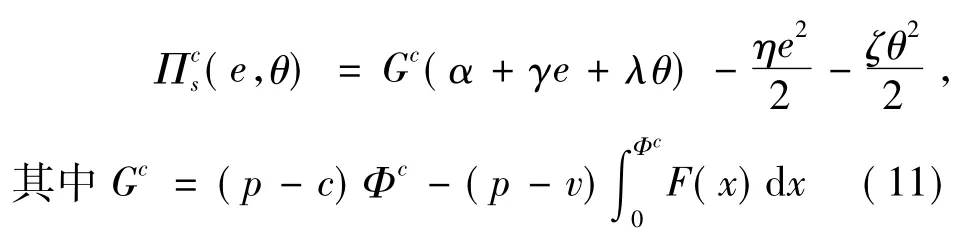
对(11)式中的e和θ分别求一阶偏导数和二阶偏导数，得

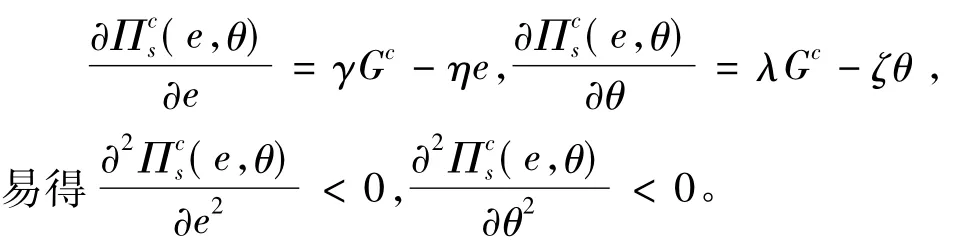
利用一阶导数的最优性知，

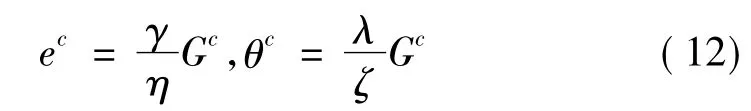
将(10)和(12)式代入(9)式可得，集中决策下供应链的期望利润为

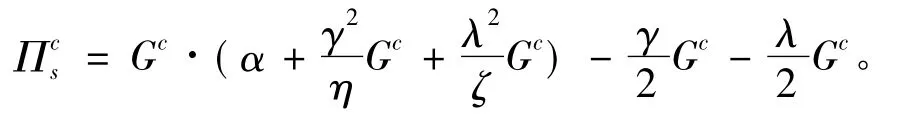
4 利润共享契约下的协调机制

在分散决策系统下，销售商会根据自身利润最大化来独立决策最优的订购量和最优的质量检验努力，而制造商会根据零售商的订单来进行生产，并且独立决策最优的质量控制努力。分散系统下，供应链成员之间单独决策会使得供应链处于次优的状态，因此，有必要设计一个行之有效的契约，使得供应链中各成员愿意采取集中决策下的最优策略，从而让供应链系统的利润最大化。本文用收益共享契约来使得供应链达到协调，要求其具体内容为:制造商将生产出来的产品以批发价格w卖给销售商，制造商索要的批发价格要等于或小于其相应的生产成本c，但要求分享一定比例的销售商利润，其中双方的利润共享系数定义为φ(0＜φ＜1)。

在收益共享契约下，销售商的期望利润为

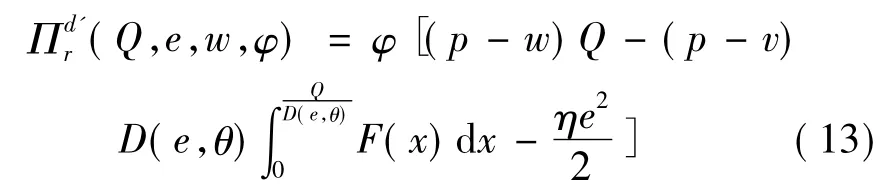
将(14)代入13式可得

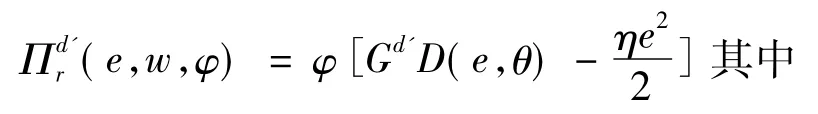
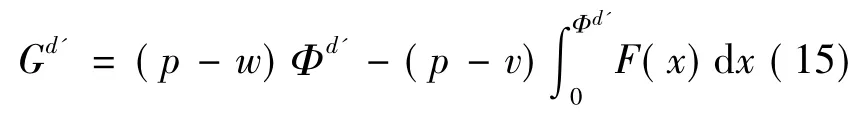
因此，销售商的期望利润为

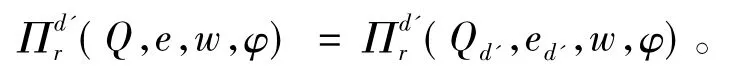
在收益共享契约下，制造商的期望利润为

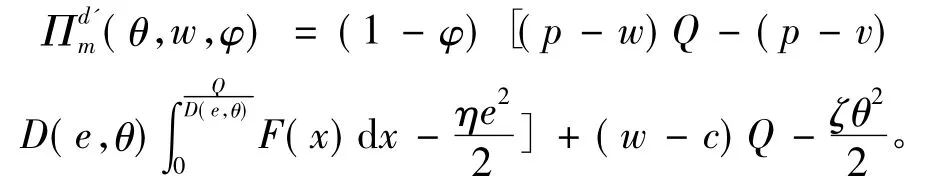
在制造商主导的Stackelberg博弈中，制造商向零售商提供的契约为(φ，wd'，θd')，零售商在这收益共享契约下期望利润不低于分散决策下的期望利润，否则零售商不可能接受该契约。从而，假设在收益共享契约下能实现供应链的完美协调，则要求在契约下供应链分散决策时制造商和零售商的收益和等于集中决策下供应链的总收益，即

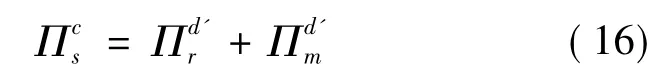
通过分析，可知，如果使(16)条件成立，则有

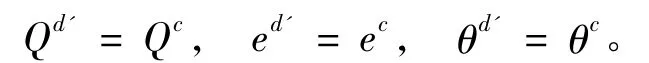
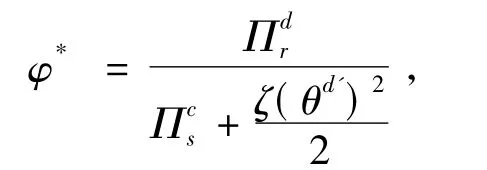
定理1如果利润共享契约中wd'=c和利润共享系数φ=φ*时，该契约能使供应链达到完美协调，但供应链成员间不能任意分割系统增加的利润。

因此，在实际的市场运作中，该契约主要应用于制造商占主导地位，掌握着市场的领导权，而零售商在供应链中只能索取其保留利润，其余的供应链系统利润全部被制造商赚取。

5 数值分析

为了进一步说明上述模型，本文进行了如下数值实验:首先，给出模型中参数值如下:α=50，p= 26，w=12，c=7，v=2，γ=4，η=6，λ=2，ζ= 5，随机变量ξ服从均值为1/a，方差为1/a2的指数分布，也即

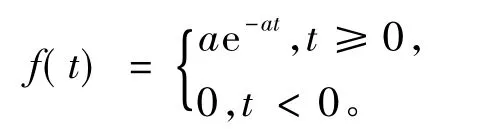
假定需求服从均值为μ=1，方差为σ=1的指数分布，利用模型中所提供的求解方法可得如下结果:①在集中决策下，制造商的最优质量控制努力水平，零售商的最优质量检验努力水平和最优订购量及系统期望利润为:

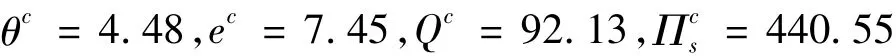
②在分散决策下，制造商的最优质量控制努力水平，零售商的最优质量检验努力水平和最优订购量及系统期望利润为:

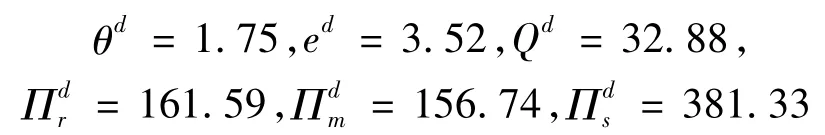
③对于收益共享契约下，当w=7和φ=0.33时，供应链能够实现完美协调。此时，制造商的最优质量控制努力水平，零售商的最优质量检验努力水平和最优订购量及系统期望利润为:

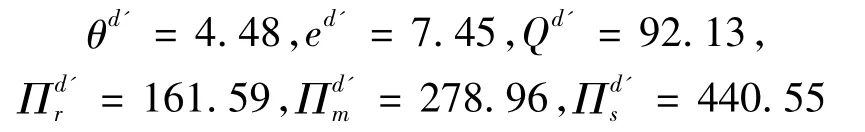
接下来，我们研究参数γ，参数λ及需求不确定性对零售商的质量检验努力，制造商的质量控制努力及供应链各成员与系统期望利润的影响。

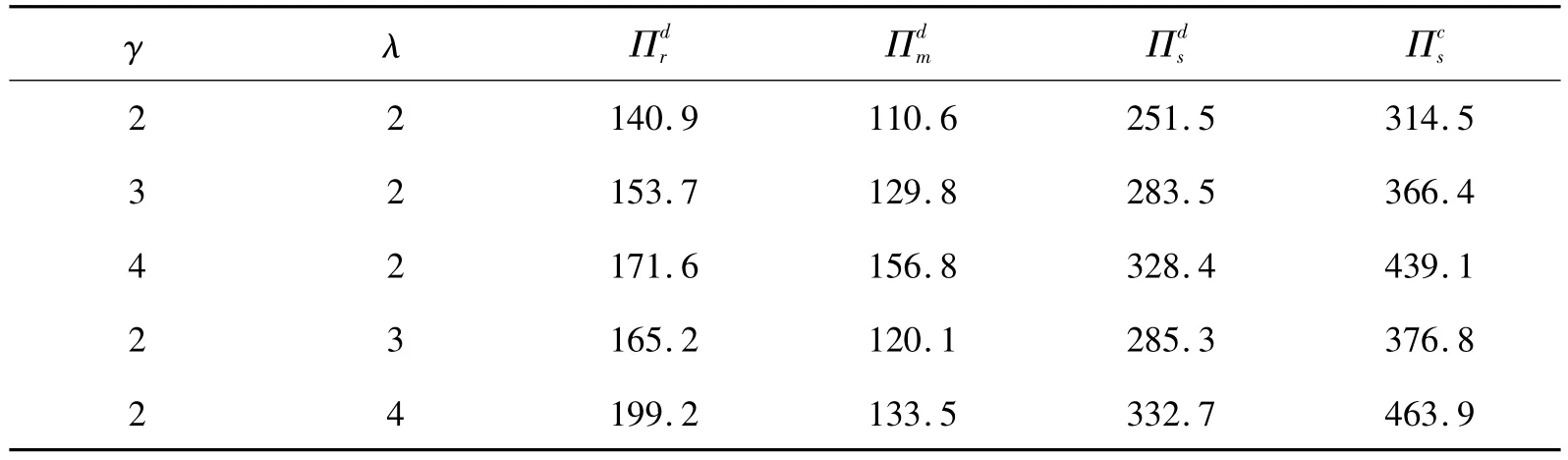
表1 参数γ和λ变化对各成员及系统期望利润的影响

根据表1可知，(1)无论是制造商质量控制努力对市场需求的影响因子还是零售商质量检验努力对市场需求的影响因子，当影响因子越大时，分散决策下各成员的期望利润将会增加，且集中决策下供应链的期望利润也增加。

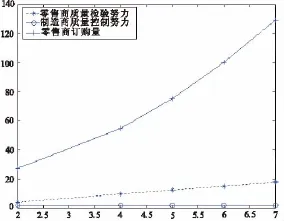
图1 参数γ对e，θ及Q的影响

(2)制造商的质量控制努力对市场需求的影响因子相对于零售商的质量检验努力对市场需求的影响因子的提高，在集中决策下供应链系统将会增加更多的期望利润。因此，不管制造商还是零售商在实际的市场运作时，都会加强产品的质量控制，产品的质量提升了，需求相对增加，从而供应链成员所获取的利润就会增加。

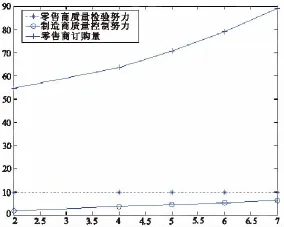
图2 参数λ对e，θ及Q的影响

由图1知，当零售商质量检验努力对市场需求影响程度增加时，零售商的质量检验努力会相应的增加，同时零售商的订购量会增加地较为明显，但对制造商的质量控制努力却没有影响。由图2知，当制造商质量控制努力对市场需求影响程度增加时，制造商的质量控制努力会相应的增加，同时零售商的订购量也有所增加，但与零售商质量检验努力对市场需求影响程度增加比较，零售商订购量增加的相对比较缓慢，同时对零售商的质量检验努力却没有影响。这说明无论是零售商还是制造商的质量努力对市场需求影响程度增加时，都会使供应链成员各自的质量努力增加但不会影响供应链中其他成员的质量努力，同时零售商的订购量也会增加，只是增加的速度不一样，因为影响程度增加会使得产品的市场需求增大，从而使得零售商的订购量增加，此时，供应链中各成员也愿意付出更多的质量努力来扩大市场需求，追求更多的利润。又由于零售商订购量增长速度不一样，在实际市场运作中，我们会更倾向于提高零售商质量检验努力对市场需求的影响程度。

本文建立在随机的市场环境下，因而考虑市场需求的不确定性对制造商和零售商的最优决策及期望利润有着重要的影响。需求的不确定性可以用需求的变异系数(coefficient of variation)来刻画，需求的变异系数等于需求的均方差与均值之比，需求的变异系数越高，需求的不确定性越大。为了便于数值计算，设定(μ，σ)分别为 (1，1)、(1/2，1/4)、(1/3，1/9)、(1/4，1/16)、(1/5，1/25)，则变异系数为σ/μ=1、0.5、0.33、0.25、0.20，令其它参数值保持不变，数值分析结果见图3和图4。

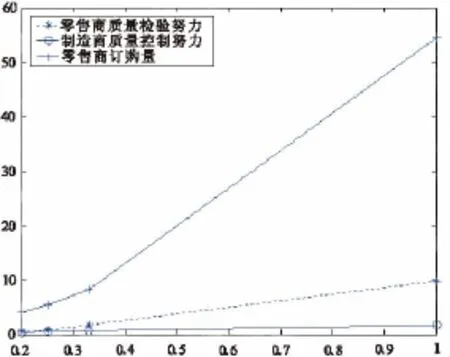
图3 需求不确定性对e，θ及Q的影响

由图3可知，当需求变异系数越大即需求不确定性越大时，制造商和零售商都将付出更多的质量努力，这意味着在市场的随机性下，制造商与零售商为了能够获取更多的利润，只有不断地增加自身的努力来提高产品的质量，从而赢得消费者对产品的信赖，提升产品的美誉度，市场需求才会不断地上升，同时当需求不确定性越大时，零售商也会增加自身的订购量，来应对需求风险。由图4可知，当需求不确定性越大时，制造商，零售商及系统的期望利润都会增加，而通常我们知需求波动性越大，各成员及系统利润会相对减少，因此，这可能有点出乎我们意料。这是因为一般模型会考虑产品的库存费用，当需求不确定性越大时，为了应对需求风险，产品的订购量增加，这就会导致模型中库存费用的增加，从而各成员及系统期望利润自然就会减少。而本文模型中并没有考虑产品的库存费用，因此，当需求不确定性越大时，各成员愿意付出更多的质量努力来提高产品的市场需求，加大零售商的产品订购量，从而使得供应链各成员及系统期望利润均会增加。所以本文模型比较适合在那些市场需求波动程度较大，产品库存费用较低或可忽略的产品中应用。

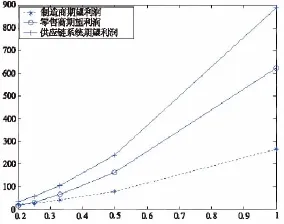
图4 需求不确定性对各成员及系统期望利润的影响

6 结束语

本文建立了在分散决策和集中决策下考虑质量控制的随机需求供应链模型，分别给出了最有订购、制造商的最优质量控制努力水平及零售商的质量检验努力水平，并在分散决策下利用收益共享契约使供应链达到完美协调。本文还有很多改进的地方，比如没有考虑需求形式是指数形式，没有考虑质量控制成本投入的信息不对称问题，以及多个制造商对多个零售商的问题等等，这些都将在后续的工作中完成。

［1］Bowon K，Chulsoon P.Supply chain coordination between supplier and retailer in a VMI relationship［J］.The Business Review Cambridge，2010，15(2):165-170.

［2］Kaynak H，Hartley J L.A replication and extension of quality management into the supply chain［J］.Journal of Operations Management，2008，26(4):468-489.

［3］Foster S T.Towards rill understanding of supply chain quality management［J］.Journal of Operations Management，2008，26(2):461-467.

［4］Balachandran K R，Rajan M V.Information，contracting，and quality cost［J］.Management Science，2000，46(6):776-789.

［5］张翠华，鲁丽丽.基于供应商检验和质量努力隐匿的协同质量控制［J］.系统管理学报，2009，18(4):385-390.

［6］Baiman S，Netessine S，Kunreuther H.Procurement in supply chains when the end-product exhibits the weakest Link property，The Wharton School University of Pennsylvania［R］，2004.

［7］Tapiero C S.Consumers risk and quality control in a collaborative supply chain［J］.European Journal of Operational Research，2007，182(2):683-694.

［8］刘 强，苏 秦.供应链质量控制与协调研究评析［J］.软科学，2010，24(12):123-127.

［9］李丽君，黄小原，庄新田.双边道德风险条件下供应链的质量控制策略［J］.管理科学学报，2005，8(1):42-47.

［10］徐 庆，朱道立，李善良.不对称信息下供应链最优激励契约的设计［J］.系统工程理论与实践，2007，27 (4):27-33.

［11］Gurnani H，Erkoc M.Supply contracts in manufacturer-retailer interactions with manufacturer-quality and retailer effort-induced demand［J］.Naval Research Logistics，2008，55(3):200-217.

［12］胡 军，张 镓，芮明杰.线性需求条件下考虑质量控制的供应链协调契约模型［J］.系统工程理论与实践，2013，33(3):601-609.

［13］肖 迪，潘可文.基于收益共享契约的供应链质量控制与协调机制［J］.中国管理科学，2012，20(4):67-73.

Supply chain coordination model of quality control under stochastic demand

XIA Dao-ming1，2，WANG Jun-ping2，ZHANG Bin2
(1.Department of Basis，Hefei Preschool Education College，Hefei Anhui230011，China; 2.School of Mathematics，Hefei University of Technology，Hefei Anhui230009，China)

This paper studies the quality control problem of the product in the supply chain under the stochastic market.The supply chain coordination model with demand depending on the manufacturer＇s quality control efforts and retailer＇s quality inspection efforts is developed.The effect of manufacturer＇s quality control efforts and retailer＇s quality inspection efforts on the retailer＇s order quantity is analyzed.The optimal quality control efforts of the manufacturer，the optimal quality inspection efforts of retailer and the optimal order quantity of retailer are given under decentralized decision and centralized decision system，respectively.A profit sharing contract is proposed to achieve perfect coordination of supply chain.Finally，the numerical example is presented to illustrate the model.

random demand;quality control;profit sharing contract;perfect coordination

O227

：A

：1004-4329(2015)01-071-07

2014-11-06

安徽省自然科学基金项目(1508085MG141)资助。

夏道明(1972－)，男，研士生，高级讲师。研究方向：应用统计与风险决策。