一个可证安全的高效的代理盲签名方案*

周 明,王 箭

(南京航空航天大学计算机科学与技术学院,江苏 南京 210016)

一个可证安全的高效的代理盲签名方案*

周 明,王 箭

(南京航空航天大学计算机科学与技术学院,江苏 南京 210016)

代理盲签名结合了代理签名和盲签名的优点，在电子商务等领域有着广阔的应用前景。目前大多数代理盲签名的安全性是启发式分析，没有形式化证明，并且大多没有考虑多一伪造攻击。提出了一个新型的代理盲签名安全模型，并在该模型下提出了一个基于双线性对的代理盲签名方案，并在随机预言机模型下，证明了其在选择消息/授权文件攻击下是不可伪造的，其安全性可分别规约为CDH问题和Chosen-Target CDH问题。分析表明,该方案满足代理盲签名的主要安全要求，而且和已有的方案相比，本方案更加高效。

代理盲签名；双线性对；随机预言机；多一伪造

1 引言

1983年，Chaum D[1]首次提出了盲签名的概念，盲签名方案要求签名者在不知道待签名消息的具体内容情况下对消息进行签名，并且签名者无法将公布的消息与自己所签的消息联系起来。由于具有这些特性，盲签名在现实生活中有着广泛的应用，如电子现金、电子投票等。代理签名的概念是Mambo M等人[2]于1996年首先提出的，在一个代理签名方案中，一个被指定的代理签名者可以代表原始签名者生成有效的签名。

结合代理签名和盲签名特点，在2000年，Lin W D和Jan J A[3]首次提出了代理盲签名方案。代理盲签名在实际应用[4]中起着重要作用，所以代理盲签名一提出便受到广泛关注。迄今为止，人们已提出了多种代理盲签名方案，如基于离散对数的代理盲签名方案[5]、基于身份的代理盲签名方案[6,7]、无证书代理盲签名方案[8]等。目前，很多代理盲签名方案都是启发式解释其安全性，没有严格的形式化证明。如Tan方案[4]解释其安全性，但文献[9]认为Tan方案[4]存在各种安全问题。设计一个安全高效的代理盲签名方案并证明其安全性具有重要的意义，也是有一定挑战性的问题。

本文在分析Huang方案[10]的代理签名安全模型的基础上，结合Pointcheval D等人[11]关于盲签名抵抗 one -more forgery的思想，提出了一个新的代理盲签名安全模型，相比其他模型，更符合代理盲签名的安全需求。同时，设计了一个可证安全的高效的代理盲签名方案，消除了签名过程中的双线性对计算，以提高签名效率。

本文第2节介绍相关的背景知识和定义；第3节提出了新的代理盲签名安全模型；第4节提出一个高效的代理盲签名方案；第5节给出方案安全性的形式化分析；第6节将本方案与和文献[12,13]的方案进行比较; 第7节总结全文。

2 预备知识

2.1 双线性映射(Bilinear Pairing)

令G1、G2是两个q阶循环群,其中q为素数。Q是G1的生成元。双线性映射e:G1×G1→G2而且满足如下条件：

(2)非退化性：e(Q,Q)≠1；

(3)可计算性：对于Q1,Q2∈G1存在有效算法来计算e(Q1,Q2)。

2.2 困难问题假设

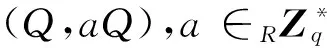
定义4Chosen-Target CDH假设：不存在概率多项式时间算法A，以不可忽略的概率解决Chosen-Target CDH问题。

定义5多一伪造(One-more Forgery)[11]：对于多项式有界整数l，(l,l+1) forgery是指一个概率多项式时间敌手A在和签名者进行l次交互后，以不可忽略的概率生成l+1个签名。

3 代理盲签名方案的定义及安全模型

3.1 代理盲签名方案的定义

在代理盲签名中有三个参与者，即原始签名人O、代理签名人P和签名请求者U。代理盲签名PBS(Proxy Blind Signature)由如下算法组成：

(1)系统参数设置算法(Setup):输入安全参数1k，生成系统参数para。

(2)密钥生成算法(KeyGen):输入安全参数1k、系统参数para，生成原始签名人O和代理签名人P的公私钥对(xi,PKi)，i∈{O,P}。

(3)代理授权算法(DelegationGen)：输入原始签名人的私钥xo以及代理授权文件ω。授权文件ω中明确地描述了授权关系、原始签名人和代理签名人的身份信息或公钥信息、允许签署的消息范围及期限等。原始签名人对授权文件ω签名，输出代理授权证书σω。

(4)代理授权验证算法(DelegationVerify)：输入原始签名人O的公钥PKo、代理授权证书σω，代理签名者验证σω是否有效。若有效则接受该代理授权；反之，则拒绝或要求O重新授权。

(5)代理签名密钥生成算法(ProxyKeyGen)：输入代理授权证书σω、代理签名人私钥xp，输出代理签名密钥skp。

(6)代理盲签名算法(ProxyBlindSign)：签名请求者U对消息m执行盲化处理，输出盲化后的消息m′，P收到m′后用代理签名密钥skp和代理授权文件ω进行签名，输出相应的代理盲签名V，U对V进行脱盲处理，输出消息m的代理盲签名V′。

(7)代理盲签名验证算法(ProxyBlindSignVerify):输入原始签名人、代理签名人的公钥PKo、PKp和公开代理授权文件ω，消息m以及待验证的代理盲签名V′，若该签名V′有效，则算法输出TRUE，否则输出⊥。

一个安全的代理盲签名必须具有以下特性：正确性、盲特性[ 15]和不可伪造性。

定义6(正确性(Correctness)) 签名人执行签名算法后，用户输出了签名V′，如果对于任意常数c和充分大的数n满足Pr[Verify(m,ω,V′)=TRUE]>1-n-c，则称代理盲签名是正确的。

定义7(盲特性[15](Blindness)) 假设S是一个敌意签名者，S和两个诚实用户U0、U1参与下面游戏：

(1)输入安全系数1k，运行系统设置算法和密钥生产算法获得签名人的公私钥对(pk,sk)。

(2)S选择两个不同的消息(m0,m1)。

(3)随机选择b∈R{0,1}(S不知道b)，发送mb给用户U0，m1-b给用户U1。

(4)S分别和U0、U1执行盲签名交互协议。

(5)如果U0、U1各自得到签名σ(mb)、σ(m1-b)，将签名发给S，否则将⊥交给S。

(6)S输出b′∈{0,1}。

如果b′=b，S知道了消息和对应签名，这时称S赢得了游戏。如果对于任意概率多项式时间算法S，其赢得上面游戏的概率至多为1/2+k-c，其中k为充分大的数，c为常数。那么，称这个签名具有盲特性。

3.2 代理盲签名方案的安全模型

2003年，Boldyreva A等人[16]给出代理签名方案的形式化安全模型，并给出了一新的方案，但该模型存在代理签名密钥泄露攻击。2006年，Huang X等人[10]把敌手分为三种类型，进一步改进Boldyreva A的安全模型。2011年Tan Z[4]基于Huang X等人的安全模型提出了一个改进，说明所提方案的不可伪造性。然而，Tan Z的模型只考虑代理签名人不可伪造性和抵抗多一伪造[11]，没有考虑恶意原始签名攻击，Yu Y[9]指出恶意原始签名人可以产生任意授权证书以及任意代理人的代理签名密钥。

结合Huang X的代理签名的安全模型和盲签名特性，本文提出了一个新的代理盲签名的安全模型。

为了更好地描述代理盲签名的不可伪造性，本文将拥有不同信息的敌手分为三类：

类型I：敌手Α1拥有原始签名人与代理签名人的公钥和原始签名人的私钥。

类型II:敌手Α2拥有原始签名人与代理签名人的公钥和代理签名人的私钥。

类型III:敌手Α3拥有原始签名人与代理签名人的公钥，能和签名人并发或交叉执行盲签名协议。

三类敌手模拟三类攻击，其目标是伪装原始签名人或者代理签名人或者用户以产生有效的签名：敌手Α1模拟恶意原始签名者，敌手Α2模拟恶意代理签名者，敌手Α3模拟恶意用户。一个安全的代理盲签名方案应该满足：Α1不能模拟代理签名人进行代理盲签名；Α2没有原始签名者的授权，不能进行代理盲签名；Α3在获得n个有效的代理盲签名后，不能根据这n个签名生成一个新的有效签名。

(1)敌手Α1的不可伪造性(Unforgeability Against Α1):

如果代理签名人没有生成过消息m在授权文件ω下的代理盲签名V′，敌手Α1生成一个有效的代理盲签名(m,ω,V′)的成功概率可以忽略不计，那么这个代理盲签名能够抵抗Α1伪造攻击。

下面来描述敌手Α1和挑战者C之间的交互。

设置：C运行Setup算法得到系统参数para，运行KeyGen算法生成原始签名人和代理签名人的公私钥对(xo,PKo)、(xp,PKp)，然后将(xo,PKo)、PKp发送给敌手Α1。

代理盲签名询问：Α1向挑战者C询问(m,ω)的代理盲签名，C运行代理盲签名算法获得关于消息m在授权文件ω下的代理盲签名V并返回给Α1。

输出：敌手Α1输出消息签名组(m*,ω*,V′*)，如果(m*,ω*,V′*)满足下列条件：

①敌手Α1没有询问过(m*,ω*)的代理盲签名；

②(m*,ω*,V′*)是一个有效的代理盲签名。

则称敌手Α1赢得了游戏，定义Α1赢得游戏的概率为Adv(A1) 。

定义8敌手Α1适应性选择消息/授权文件攻击代理盲签名方案，如果在时间t内，经过至多qHi次H1-哈希询问i∈{1,2}和qPBS次代理盲签名询问最后赢得游戏的概率Adv(A1)至少为ε，那么称敌手Α1能够(t,qH1,qH2,qPBS,ε)-攻破代理盲签名方案。如果不存在敌手Α1能够(t,qH1,qH2,qPBS,ε)-攻破，那么称方案是(t,qH1,qH2,qPBS,ε)-安全的。

(2)敌手Α2的不可伪造性(Unforgeability Against Α2):

如果原始签名人没有将授权文件ω授权给敌手Α2，敌手Α2生成一个有效的授权文件ω的证书σω的概率可以忽略不计，那么这个代理盲签名能够Α2抵抗伪造攻击。

下面来描述敌手Α2和挑战者C之间的交互。

设置：C运行Setup算法得到系统参数para，运行KeyGen算法生成原始签名人和代理签名人的公私钥对(xo,PKo)、(xp,PKp)，然后将PKo、(xp,PKp)发送给敌手Α2。

代理授权询问：Α2向挑战者C询问授权文件ω的授权，C运行代理授权算法得到授权文件ω的授权证书σω并返回给Α2。

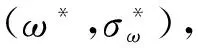
①敌手Α2没有询问过ω*的授权证书；

则称敌手Α2赢得了游戏，定义Α2赢得游戏的概率为Adv(Α2)。

定义9敌手Α2适应性选择消息/授权文件攻击代理盲签名方案，如果在时间t内，经过至多qH1次随机预言机询问和qDG次授权询问最后赢得游戏的概率Adv(Α2)至少为ε，那么称敌手Α2能够(t,qH1,qDG,ε)-攻破代理盲签名方案。如果不存在敌手Α2能够(t,qH1,qDG,ε)-攻破，那么称方案是(t,qH1,qDG,ε)-安全的。

(3)敌手Α3的多一不可伪造性(One-more Unforgeability Against Α3):

下面描述敌手Α3和挑战者C之间的交互。

设置：C运行Setup算法得到系统参数para，运行KeyGen算法生成原始签名人和代理签名人的公私钥对(xo,PKo)、(xp,PKp)，然后将系统参数para、原始签名人和代理签名人公钥(PKo,PKp)发送给敌手Α3。

代理授权询问：Α3向挑战者C询问授权文件ω的授权，C先运行代理授权算法得到授权文件ω的授权证书σω并返回给Α3。

代理盲签名询问：Α3向挑战者C询问(m,ω)的代理盲签名，挑战者C都将配合Α3运行一次盲签名协议，这里允许Α3并发或交叉地要求执行多个盲签名。令qPBS为代理盲签名询问的次数。

①((mi,ωi)≠(mj,ωj)),i≠j,任意i,j∈1,…,l；

②l严格大于qPBS。

则称敌手Α3赢得了游戏，定义Α3赢得游戏的概率为Adv(A3)。

定义10敌手Α3并发适应性选择消息代理盲签名方案，如果在时间t内，经过至多qDG次授权询问和qPBS次代理盲签名询问最后赢得游戏的概率Adv(A3)至少为ε，那么称敌手Α3能够(t,qDG,qPBS,ε)-攻破代理盲签名方案。如果不存在敌手Α3能够(t,qDG,qPBS,ε)-攻破，那么称方案抵抗适应性选择消息下的多一伪造攻击(t,qDG,qPBS,ε)-安全的。

定义11(不可伪造性(Unforgeability)) 如果不存在Α1、Α2、Α3在适应性选择消息/授权文件攻破代理盲签名方案，那么称代理盲签名是不可伪造的。

4 一个安全的代理盲签名方案

在这一节中，将利用双线性对构造一个新的可证明安全的代理盲签名方案，而且该方案中签名过程去掉了双线性对计算，以提高签名效率。代理盲签名中一般包含三方： 原始签名人、代理签名人和签名请求者U。代理盲签名方案由以下算法组成：

(1)系统参数设置(Setup)：令G1、G2是q阶循环群，其中q为素数，Q是G1的生成元,双线性映射e:G1×G1→G2，定义两个哈希函数H1、H2:{0,1}*→G1。系统参数 para={G1,G2,q,e,Q,H1,H2}。

(2)密钥生成算法(KeyGen):该算法生产原始签名人O的公私钥对(xo,PKo=xoQ)和代理签名人P的公私钥对(xp,PKp=xpQ)。

(3)代理授权算法(DelegationGen)：原始签名人产生授权文件ω∈{0,1}*，该文件描述了授权关系、原始签名人和代理签名人的身份信息、允许签署的消息范围及期限等。原始签名人O对代理签名人P进行代理授权，O计算σω=xoH1(ω)，然后O把授权证书σω发送给代理签名人，公开授权文件ω。

(4)代理授权验证算法(DelegationVerify):代理签名人验证e(σω,Q)=e(H1(ω),PKo)是否成立，若成立，代理签名人接受授权证书σω；否则代理签名人要求原始签名人重新发送授权证书，或者终止协议。

(5)代理签名密钥生成算法(ProxyKeyGen)：代理签名人收到有效的授权证书σω，然后生成代理签名密钥skp=(σω,xp)。

(6)代理盲签名算法(ProxyBlindSign):该算法是代理签名人P和签名请求者U执行盲签名交互协议的过程。

①消息发布：签名请求者U给代理签名人P发出对消息m∈{0,1}*签名的请求。

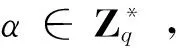
R′=βR=αβH1(ω)

R1=r1H2(m‖ω)+r2Q

R2=r1β

发送R1、R2给代理签名人P。

④Signing：P计算V=xpR1+αR2σω，并发送V给U。

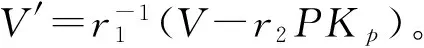
(7)代理盲签名验证算法(ProxyBlindVerify)：验证者收到签名δ=(m,ω,R′,V′)后，检验等式：

e(V′,Q)=e(H2(m‖ω),PKp)e(R′,PKo)

5 安全性分析

在这一节中，将分析这个代理盲签名方案安全性的三个方面：正确性、盲特性和不可伪造性。

5.1 正确性

定理1该代理盲签名方案满足正确性。

证明

r1αβσω-r2PKp),Q)=

e(xpH2(m‖ω)+αβσω,Q)=

e(xpH2(m‖ω),Q)e(αβxoH1(ω),Q)=

e(H2(m‖ω),PKp)e(R′,PKo)

□

5.2 盲特性

定理2该代理盲签名方案具有盲特性，签名者无法得到关于被签名消息的任何消息。

R′=βR=αiβH1(ω)

(1)

R1i=r1H2(m‖ω)+r2Q

(2)

R2i=r1β

(3)

(4)

从等式(1)中可以推导出β是唯一存在的。又r1=β-1R2i，所以r1也是唯一存在的。同理也存在唯一的盲因子r2满足r2Q=R1i-r1H2(m‖ω‖U′)，最后证明(r1,r2,β)也满足等式(4)。推导如下：

因为(m,ω,R′,V′)是有效的签名，所以e(V′,Q)=e(H2(m‖ω),PKp)e(R′,PKo)。即：

e(V′,Q)=e(H2(m‖ω),PKp)e(R′,PKo)=

e(H2(m‖ω)xp,Q)e(αiβxoH1(ω),Q)=

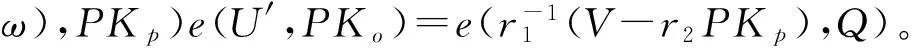
因此，盲因子(r1,r2,β)总是存在，即使有无限能力的S能成功决定b的概率仍为1/2。因此,本文提出的代理盲签名方案具有盲特性。

□

5.3 不可伪造性

定理3在随机预言机模型下，Α1适应性选择消息/授权文件攻击该代理盲签名方案，如果能够(t,qH1,qH2,qPBS,ε)-攻破，那么存在一个(t′,ε′)算法C解决CDH问题。(t′,ε′)满足：

t′≤t+(qH1+qH2+3qPBS+2)tsm+(qPBS+1)tadd

其中，e为自然常数，tsm为计算G1群上的标量乘的时间，tadd为计算G1群上的加法时间。

证明假定存在敌手Α1能够(t,qH1,qH2,qPBS,ε)-攻破代理盲签名方案，那么算法C能利用Α1解决CDH问题。算法C的挑战是：在C已知X*=x Q,Y*=y Q的条件下，计算xyQ。算法C模拟挑战者与Α1进行交互，具体的交互过程如下：

(2)H1-预言询问：C维护LH1列表(ω,h,H)，当Α1对ω进行H1(ω)询问时，C应答如下：

①如果ω在列表LH1存在，返回Α1的询问H1(ω)=H。否则执行②；

(3)H2-预言询问：C维护LH2列表(ω,m,B,b,c)，当Α1对(m,ω)进行H2(m‖ω)询问时C应答如下：

①如果(ω,m,B,b,c)在列表LH2存在，返回Α1的询问H2(m‖ω)=B。否则执行②；

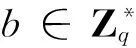
B=H2(m‖ω)=cbQ+(1-c)bX*=

最后C增加一个元组(ω,m,B,b,c)到列表LH2，并回答Α1的询问H2(m‖ω)=B。

(4)代理盲签名询问：C维护LPBS列表(m,ω,r,R′,V′)，当Α1对(m,ω)进行代理盲签名询问，C应答如下：如果(m,ω)在列表LPBS存在，返回Α1代理盲签名询问(m,ω,R′,V′)。否则执行下面的步骤：

①C查询LH2得到包含(m,ω)的元组(ω,m,B,b,c)。

②如果c=0，C中止。

(5)输出：最后Α1中止，输出一个有效消息签名对(m*,ω*,R′*V′*)，而(m*,ω*)没有经过代理盲签名询问。算法C在LH2找到元组(ω*,m*,B,b,c)，然后执行下面的步骤：

①如果c=1，C中止。

②如果c=0，H2(m*‖ω*)=bX*，C输出b-1(V′*-xoR′*)作为xyQ的一个实例，解决了CDH问题。因为(m*,ω*,R′*V′*)是一个有效的代理盲签名。所以:

e(V′*,Q)=e(H2(m*‖ω*),PKp)e(R′*,PKo)⟹

e(V′*,Q)=e(bX*,Y*)e(R′*,xoQ)⟹

e(V′*,Q)=e(bxQ,yQ)e(xoR′*,Q)⟹

e(V′*-xoR′*,Q)=e(bxQ,yQ)⟹

e(b-1(V′*-xoR′*),Q)=e(xyQ,Q)

推导出:e(b-1(V′*-xoR′*),Q)=e(xyQ,Q)，由双线性对的非退化性有：e(b-1(V′*-xoR′*),Q)=e(xyQ,Q)⟺b-1(V′*-xoR′*)=xyQ。因此，C可以输出b-1(V′*-xoR′*)作为xyQ的一个实例，解决了CDH问题。

□

现在我们分析算法C成功解决CDH问题的概率和时间。这里考虑三个事件E1、E2、E3：

E1：对于Α1代理盲签名询问，C没有中止。

E2：Α1输出了一个有效的签名(m*,ω*,R′*,V′*)。

E3：事件E2发生，而且LH2中包含ω*的元组中的c=0。只有当上述所有事件都发生，C才能成功。即：

P(Csuccess)=P(E1∧E2∧E3)=

P(E1)P(E2|E1)P(E3|E1∧E2)

引理1当Α1代理盲签名询问时，C没有中止的概率至少为(1-1/(qPBS+1))qPBS，即P(E1)≥(1-1/(qPBS+1))qPBS。

证明因为Α1每一次代理授权询问，C没有中止的条件是c=1，而Pr[c=1]=1-1/(qPBS+1)，又Α1至多qPBS次代理盲签名询问，所以P(E1)≥(1-1/(qPBS+1))qPBS。

□

引理2如果经过Α1代理盲签名询问后算法C没有中止，P(E2|E1)≥ε。

引理3Α1输出一个有效的签名，C没有中止的概率至少为1/(qPBS+1)，所以P(E3|E1∧E2)≥1/(qPBS+1)。

根据引理1,2,3有，C成功解决CDH问题的概率为：

ε′=P(Csuccess)=

P(E1)P(E2|E1)P(E3|E1∧E2)≥

在Setup阶段，C需要1次G1群上的标量乘法运算；在H1-预言询问阶段，需要1次G1群上的标量乘法运算；在H2-预言询问阶段，需要1次G1群上的标量乘法运算；在代理盲签名询问阶段，需要3次G1群上的标量乘法运算和1次G1群上的加法运算；在输出阶段，需要2次G1群上的标量乘法运算和1次G1群上的加法运算。所以，C运行的时间为t+(qH1+qH2+3qPBS+2)tsm+(qPBS+1)tadd。运行算法C时间t′的界限为：

t′≤t+(qH1+qH2+3qPBS+2)tsm+(qPBS+1)tadd

定理4在随机预机模型下，Α2适应性选择消息/授权文件攻击该代理盲签名方案，如果能够(t,qH1,qDG,ε)-攻破，那么存在一个(t′,ε′)算法C解决CDH问题。(t′,ε′)满足：

t′≤t+(qH1+qDG+2)tsm

其中，e为自然常数，tsm为计算G1上的标量乘的时间。

证明与定理3证明类似，假定存在敌手Α2能够(t,qH1,qDG,ε)-攻破代理盲签名方案，那么算法C能利用Α2解决CDH问题。算法C的挑战是：在C已知X*=xQ,Y*=yQ的条件下，计算xyQ。算法C模拟挑战者与Α2进行交互，具体的交互过程如下：

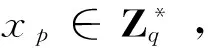
(2)H1-预言询问：C维护LH1列表(ω,B,b,c)，当Α2对ω进行H1(ω)询问时，C应答如下：

①如果ω在列表LH1存在，返回Α1的询问H1(ω)=B。否则执行②；

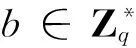
B=H1(ω)=cbQ+(1-c)bX*=

最后C增加一个元组(ω,B,b,c)到列表LH1并回答Α1的询问H1(ω)=B。

(3)代理授权询问：C维护LDG列表(ω,σω)，当Α2要求对授权文件ω授权查询时，C应答如下：如果ω在列表LDG存在，返回Α2代理授权询问σω。否则执行下面的步骤：

①C查询LH1得到包含ω的元组(ω,B,b,c)。

②如果c=0，C中止。

③如果c=1，C计算σω=bPKo，返回(ω,σω)作为Α2的应答；并增加一个元组(ω,σω)到列表LDG。

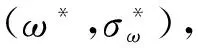
①如果c=1，C中止。

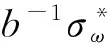
e(bxQ,yQ)=e(bxyQ,Q)⟹

由双线性对的非退化性得到：

⟺

与定理4证明类似地有，C成功解决CDH问题的概率和时间为：

t′≤t+(qH1+qDG+2)tsm

□

定理5在随机预机模型和Chosen-Target CDH难题假设下，该代理盲签名方案能够抵抗敌手Α3的One-more Forgery攻击。

证明假定Α3适应性选择消息/授权文件的模式下One-more Forgery攻击该代理盲签名方案，那么算法C能利用Α3的能力解决Chosen-Target CDH问题。算法C模拟挑战者与Α3进行交互，具体的交互过程如下：

(2)H1-预言询问：C维护LH1列表(ω,h,H)，当Α3对ω进行H1(ω)询问时，C应答如下：

①如果ω在列表LH1存在，返回Α3的询问H1(ω)=H。否则执行①。

(3)H2-预言询问：C维护LH2列表(ω,m,Z)，当 Α3对(m,ω)进行H2(m‖ω)询问时，C应答如下：

①如果(ω,m,Z)在列表LH2存在，返回Α3的询问H2(m‖ω)=Z。否则执行②；

②C询问目标预言机ΘT获得一个随机点Z∈G1，然后增加元组(ω,m,Z)到列表LH2，并回答Α3的询问H2(m‖ω)=Z。

(4)代理授权询问：C维护LDG列表(ω,σω)，当Α3要求对授权文件ω授权查询时，C应答如下：

①如果ω在列表LDG存在，返回Α2代理授权询问σω。否则执行②。

②C查询LH1得到包含ω的元组(ω,h,H),C计算σω=xoH，返回Α2代理授权询问σω。

(5)代理盲签名询问：当Α3询问(ω,R′,R1,R2)的签名，C将R1作为输入询问帮助预言机ΘH，返回Ra=aR1给C，C查询列表LDG得到包含ω的元组(ω,σω)，C计算V=Ra+αR2σω，然后返回V作为Α3的代理盲签名询问。

所以，C输出{(Z1,O1),(Z2,O2),…,(Zl,Ol)};qT=qPBS

□

定理6该代理盲签名是不可伪造的。

证明根据定理3～定理5可知，本文所提代理盲签名能抵抗Α1、Α2、Α3在适应性选择消息/授权文件下的攻击。所以，由定义11可以推论出该代理盲签名是不可伪造的。

□

6 性能分析

第3节的方案和代理盲签名方案[12,13]在计算量和安全性的对比如表1所示。表1符号定义：Pa表示双线性映射中的对运算，Pm表示G1群上的标量乘运算，Ad表示G1群上的加法运算。

在计算量上，根据文献[17]的研究，双线性对运算计算最耗时，从表1中可以看出：新方案的双线性对运算是5次，比文献[12,13]方案的运算次数都要少，新的方案的计算复杂度大约为5Pa+8Pm+3Ad，而文献[12,13]方案的计算复杂度分别为7Pa+7Pm+6Ad和7Pa+8Pm+7Ad。因为文献[12,13]方案在签名过程采用的G2群元素的指数运算，而G2群元素是通过双线性运算生成的，所以计算效率低。而新方案改为G1标量乘法运算，消除了代理盲签名过程中的双线性对运算，提高了效率，因此新方案比文献[12,13]方案都要高效。

在安全性上，文献[12,13]方案在不可伪造性只分析了原始签名人、代理签名人的不可伪造攻击，而没有考虑方案能否抵抗敌手通过获得n个签名来生成n+1个签名的情况(多一伪造[11])。新方案考虑了三类敌手攻击，并在建立了安全模型，在随机预言机模型下证明了方案的不可伪造性。所以，新方案比文献[12,13]方案更符合代理盲签名的安全需求。

7 结束语

本文根据代理盲签名的安全特性，设计了一个新的安全模型，相对其他模型，能抵抗更强的攻击者。本文提出了一个基于双线性对的代理盲签名方案。本方案的安全性建立在CDH假设和Cho-sen Target CDH假设之上，并在随机预言机模型下证明了方案是安全的。另外，本方案比文献[12,13]的方案高效，能应用于条件受限环境下的电子现金。设计标准模型下的安全代理盲签名和安全的电子现金协议是我们下一步的研究方向。

Table 1 Comparison of our scheme with others in computation overhead and security表1 本方案与其他方案在计算量和安全性比较

[1] Chaum D. Blind signatures for untraceable payments[C]∥Proc of Advances in Cryptology,1983:199-203.

[2] Mambo M,Usuda K,Okamoto E. Proxy signatures:Delegation of the power to sign messages[J].IEICE Transactions on Fundamentals of Electronics,Communications and Computer Sciences,1996,79(9):1338-1354.

[3] Lin W D,Jan J K.A security personal learning tools using a proxy blind signature scheme[C]∥Proc of International Conference on Chinese Language Computing,2000:273-277.

[4] Tan Z.An off-line electronic cash scheme based on proxy blind signature[J].The Computer Journal,2011,54(4):505-512.

[5] Su J,Liu J. A proxy blind signature scheme based on DLP[C]∥Proc of 2010 International Conference on Internet Technology and Applications,2010:1-4.

[6] Zhang Q,Wen Q,Chen G. Efficient ID-based proxy blind signature scheme[J]. Wuhan University Journal of Natural Sciences,2007,12(1):105-108.

[7] Gu C,Zhu Y. An efficient ID-based proxy signature scheme from pairings[C]∥Proc of Information Security and Cryptology,2008:40-50.

[8] Zhang B,Xu Q. Certificateless proxy blind signature scheme from bilinear pairings[C]∥Proc of the 2nd International Workshop on Knowledge Discovery and Data Mining,2009:573-576.

[9] Yu Y,Mu Y,Wang G,et al. Cryptanalysis of an off-line electronic cash scheme based on proxy blind signature[J].The Computer Journal,2011,54(10):1645-1651.

[10] Huang X, Mu Y, Susilo W, et al. A short proxy signature scheme:Efficient authentication in the ubiquitous world [C]∥Proc of EUC 2005 Workshops on Embedded and Ubiquitous Computing,2005:480-489.

[11] Pointcheval D, Stern J. Provably secure blind signature schemes[C]∥Proc of Advances in Cryptology(ASIACRYPT’96),1996:252-265.

[12] Huang R,Nong Q.Security analysis of a proxy blind signature and its improved scheme[C]∥Proc of International

Conference on Information Technology,Computer Engineering and Management Sciences,2011:179-182.

[13] Zhang Ni,Xi Xue-feng,Lu Wei-zhong.Analysis and improvement of identity-based proxy blind signature scheme[J].Computer Engineering,2010,16(42):110-112.(in Chinese)

[14] Boldyreva A. Threshold signatures,multisignatures and blind signatures based on the gap-Diffie-Hellman-group signature scheme[C]∥Proc of the 6th International Workshop on Theory and Practice in Public Key Cryptography,2002:31-46.

[15] Gao W,Wang G,Wang X,et al. One-round ID-based blind signature scheme without ROS assumption[C]∥Proc of the 2nd International Conference on Pairing-Based Cryptography-Pairing,2008:316-331.

[16] Boldyreva A,Palacio A,Warinschi B. Secure proxy signature schemes for delegation of signing rights[J]. Journal of Cryptology,2012,25(1):57-115.

[17] Barreto P S L M,Galbraith S D,ó’héigeartaigh C,et al.Efficient pairing computation on supersingular abelian varieties[J]. Designs,Codes and Cryptography,2007,42(3):239-271.

附中文参考文献:

[13] 张妮,奚雪峰,陆卫忠,等. 基于身份的代理盲签名方案分析与改进[J].计算机工程,2010,16(42):110-112.

周明(1990-),男,湖南澧县人，硕士,研究方向为代理盲签名。E-mail:540195111@qq.com

ZHOU Ming,born in 1990,MS,his research interest includes proxy blind signature.

王箭(1968-),男,江苏南京人，博士,教授,CCF会员(E200019557M),研究方向为信息安全与应用密码学。E-mail:wangjian@nuaa.edu.cn

WANG Jian,born in 1968,PhD,professor,CCF member(E200019557M),his research interests include information security, and applied cryptography.

An efficient and provably secure proxy blind signature scheme

ZHOU Ming,WANG Jian

(College of Computer Science and Technology，Nanjing University of Aeronautics and Astronautics，Nanjing 210016,China)

By combining the advantages of blind signatures with proxy signatures, a proxy blind signature can be widely applied in many fields, such as e-commerce. Currently, most of the proposed proxy blind signature schemes only give some heuristic explanations without formal proof, and one-more forgery is seldom considered in many schemes. In the paper, we propose a novel efficient security model and a proxy blind signature scheme based on bilinear parings. The scheme is unforgeable against adaptive chosen message/warrant attacks under the Computational Diffie-Hellman assumption and Chosen-Target Computational Diffie-Hellman assumption in the random oracle model. The analysis shows that the proposed scheme can satisfy the main secure properties of a proxy blind signature. Furthermore, the scheme is more efficient than traditional ones.

proxy blind signature;bilinear pairing;random oracle model;one-more forgery

1007-130X(2015)09-1643-09

2014-10-28;

2015-02-28

TP309

A

10.3969/j.issn.1007-130X.2015.09.007

通信地址：210016 江苏省南京市雨花台区宁双路18号翠岭银河A区17栋506

Address:Room 506,Building 17,Zone A,Cuiling Yinhe,18 Ningshuang Rd,Yuhuatai Distric,Nanjing 210016,Jiangsu,P.R.China