有19-(4,f)型自同构的二元自对偶码*
王 荣,王俊新
(山西财经大学应用数学学院,山西 太原 030006)
有19-(4,f)型自同构的二元自对偶码*
王 荣,王俊新
(山西财经大学应用数学学院,山西 太原 030006)
应用二元自对偶码可看成几个自对偶码的直和理论,研究了具有19-(4,f)型自同构、码长在100以内的的二元自对偶码。这种对偶码都可看成一个码长为4的收缩码和GF(2)n上一些偶重量多项式的直和。证明了码长大于80且小于100时,不存在19-(4,f)型的二元自对偶码。根据码长较短的自对偶码分别构造出了码长为76、78和80的二元自对偶码,并给出其生成矩阵。由码的等价得到了这几类码可能的分类情况。运行Matlab程序,证明了具有19-(4,2)型和19-(4,4)型的二元自对偶码在等价情况下都有11个,19-(4,0)型的二元自对偶码在等价情况下是不存在的。
自对偶码;生成矩阵;自同构;等价
1 引言
自对偶码是一种特殊的纠错码,为使码有较强的纠错能力,需要增加码元,以增加码字间的差别,使码字的错误发生在一定的范围内,不会变成另一个码字。也就是说,按照一定规则把原来的码字变成有剩余长度的码字,并且码字的码元之间存在着一定的关系,这种关系的建立过程就是编码。码字到达接收端,用编码的规则来检验,如果不发生错误,原规则一定是适用的,否则原规则不满足。因此,可根据编码规则来判定编码过程中是否发生了错误。如果发生,在纠错能力内按照一定的规则确定位置并纠错。自对偶码在编码纠错中有非常重要的作用,清楚地知道其分类和构成情况也更为必要。长度不大于32的自对偶码的生成矩阵及分类情况已经全部解决[1]。2012年,Bouyuklieva S[2]证明了不存在有3-(12,12)和3-(14,6)型自同构的自对偶码,并且有3-(16,0)型自同构的自对偶码共有264种。同年,王荣、王俊新[3]证明了有17阶自同构的二元自对偶码[52,26,10]仅有一种。近期,王荣[4]证明有13-(4,2)型的二元自对偶码只有8个,存在16个有13-(4,4)型的二元自对偶码,有13-(4,6)型的二元自对偶码有10种。 2011年,Yorgov V[5]给出了长度为42的二元自对偶码,有7阶自同构情况时有29种。杨庆[6]构建了369种长度为38的二元自对偶极值码。2008年,樊继秋[7]考虑了码长为38的二元自对偶极值码,并给出其矩阵算法,得到了该极值码。2007年,Bouyuklieva S[8]指出有3-(14,0)型自同构的自对偶码有16 607种。本文试图解决有19阶自同构的自对偶码。
2 基础知识
对一个二元域GF(2)n上的线性码,码字的前一部分是信息自身:u1,u2,…,uk,后一部分是校验符:uk+1,uk+2,…,un,所有的码字构成了长度为n、维数为k的一个线性子空间,称为GF(2)n上的一个[n,k]线性码C。对一个线性码C,其对偶码C⊥={v|(u,v)=0,∀u∈C}((u,v)为GF(2)n上的内积),若C=C⊥,C就叫二元自对偶码。对一个自对偶码,维数必满足k=n-k,即k=n/2,n一定是偶数。对∀u=(u1,u2,…,un)∈C,u的重量wt(u)指u1,u2,…,un中非零数的个数。两个码字的距离dist(u,v)指任意两个不相同码字u=(u1,u2,…,un)和v=(v1,v2,…,vn)在相同位置上取值不相同的位数,即dist(u,v)=wt(u-v)。GF(2)n上最小距离为d的 [n,k]码称为二元自对偶[n,k,d]码。由于自对偶码是一个线性子空间,所以二元自对偶码C的最小距离是非零码字的最小wt(u)值。如果一个二元自对偶码的码字重量都能被4整除,这个码称为双偶码,否则是单偶码。
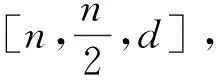
对GF(2)n上的二元自对偶码C的码字u=(u1,u2,…,un)和n次对称群Sn中的τ,定义Cτ中的元素uτ=(uτ(1),uτ(2),…,uτ(n)),则码Cτ和C称为等价的。置换τ叫码C的一个自同构。C的所有自同构的集合形成Sn的一个子群,叫码C的自同构群,用AUT(C)表示。若τ∈AUT(C),τ的阶为p,且有c个独立的循环,f个固定点,则τ有型p-(c,f)。

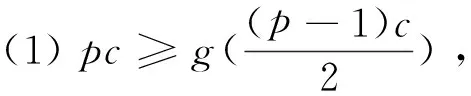
定理1对有型p-(c,f)的二元自对偶码[78,39,14],只存在p-(c,f)=19-(4,2)。
证明当p≥19时,对二元自对偶码[78,39,14],所有可能的型为:19-(4,2),19-(3,21),19-(2,40),19-(1,59),23-(3,9),23-(2,32),23-(1,55),29-(2,20),29-(1,49),31-(2,16),31-(1,47),37-(2,4),37-(1,41),41-(1,37),43-(1,35),47-(1,31),53-(1,25),59-(1,19),61-(1,17),67-(1,11),71-(1,7),73-(1,5)。应用引理2易得:除了型19-(4,2),其余的型都不可能存在。
□
定理2当码长大于80且小于100时,不存在有19-(4,f)型的二元自对偶码。
证明当码长大于80且小于100时,最小距离为16,这些码可能的自同构型为19-(4,6), 19-(4,8), 19-(4,10), 19-(4,12), 19-(4,14), 19-(4,16), 19-(4,18)和19-(4,20)。
□
2.1 码的生成矩阵
令C是有19阶自同构的二元自对偶码,根据定理1,可假设自同构具有如下形式:
σ=(1,2,…,19)(20,21,…,38)…(51,52,…,76)(77)(78)。
令Ω1=(1,2,…,19),Ω2=(20,21,…,38),Ω3=(39,40,…,57),Ω4=(58,59,…,76),Ω5=(77),Ω6=(78)。
设Fτ(C)={u∈C|uτ=u},Eτ(C)={u∈C|wt(u|Ωi)≡0(mod 2)},i=1,2,3,4.}。其中,u|Ωi指u在Ωi上的限制。由文献[1]知:C=Fτ(C)⊕Eτ(C)。

令P是GF(2)n上由x-1生成的长度为19的循环码。由于x18+x17+…+x+1是GF(2)n上的不可约多项式。域P有218个元素。令Eτ(C)*是去掉最后两位的码字,∀u ∈Eτ(C)*,u|Ωi有偶重量。作映射u|Ωi→P,即:
(u0,u1,…,u18)→u0+u1x+…+u18x18,则有φ:Eτ(C)*→P4。
引理3[9]有型p-(c,f)的线性码C是自对偶⟺下列两条件同时成立。
(1)收缩码π(Fτ(C))是自对偶码;

由引理3知,π(Fτ(C))是一个[6,3]二元自对偶码。由文献[1]得,[6,3]二元自对偶码在等价情况下只有一个,生成矩阵为:


(1)
的 [4,2]二元自对偶码。因此,假定φ(Eτ(C)*)的生成矩阵为下述矩阵:
其中,ai(x)∈P,i=1,2,3,4。e(x)=x+x2+…+x18是域P的单位元。A的两行在内积式(1)下是正交的,等价下有两种可能矩阵:
s=0,1,…,18;ti=1,2,…,27×511,i=1,2,3,4。b(x)=1+x2+x3+x6+x7+x9+x10+x11+x13+x14+x15+x18为P的本原元(阶为27×511),g(x)=xe(x),阶为19。A1的行只可能是下列四种情形:
(e(x)0e(x)0)
(e(x)0b(x)5110)
(e(x)0b(x)3×5110)
(e(x)0b(x)9×5110)
现考虑A2,由于行的正交性,得到b(x)t3+29t1=b(x)t4+29t2g(x)s,s只能为0(s>0,设b(x)t4+29t2的阶为r,g(x)s的阶为19,必有(r,19)=1,b(x)t4+29t2g(x)s的阶为19×r,所以19整除b(x)t3+29t1的阶,矛盾),因此A2可简化为:

故φ(Eτ(C)*)的生成矩阵为:
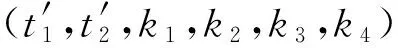

定理3有型19-(4,2)的二元自对偶码[78,39,14]的生成矩阵为:
前三行中,黑体0和1表示元素全为0和1的1×19行向量。后两行中的U和Vi(i=1,2,3,4)和前两列中的0如前所述,后两列的0表示18×1的列向量。
2.2 码的分类
引理4[9]两个有同样型(19-(4,2))的二元自对偶码C和C′,如果码C可通过对码C′进行下列变换的乘积得到,则这两个码是等价的。


(3)C中4个循环的一个置换;
(4)C中固定点的一个置换。
在矩阵A′中作变换x→x2(参考文献[10]),则:
(2)
对矩阵应用置换(1,2)(3,4)得:
(3)
应用置换(1,3)(2,4)可得:
(4)
应用置换(1,3)和(2,3)可得:
(5)
(6)
运用Matlab程序,其设计思路如下:
(1)用一个行向量表示一个多项式,并定义两多项式的加法及乘法;
(2)根据定理2中每一个黑体元素所对应的循环矩阵得到二元自对偶码[78,39,14]的生成矩阵;
(3)对生成矩阵的行、列进行线性变换,得到形如(M|I)的矩阵形式,M、I为39×39的矩阵,其中I为单位矩阵。
(4)计算矩阵M生成的任意码字间的最小距离d1,如果d1+1=14,则输出对应的参数,否则继续下一次循环。
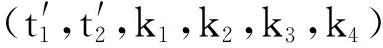
(93,476,16,8,11,25) (77,182,2,4,14,19)
(77,182,0,1,19,23) (29,118,0,2,3,24)
(23,428,6,6,6,6) (27,467,6,16,19,21)
(9,388,15,1,3,15) (9,388,3,19,23,11)
(3,342,13,19,26,17) (3,342,11,7,9,17)
(3,342,8,6,12,22)
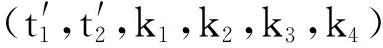
定理4有型19-(4,2)的二元自对偶码[78,39,14]在等价情况下共有11种:C1,C2,…,C11。
C1的生成矩阵如图1所示。
3 有相似性自同构的二元自对偶码
3.1 p-(c,f)=19-(4,4)
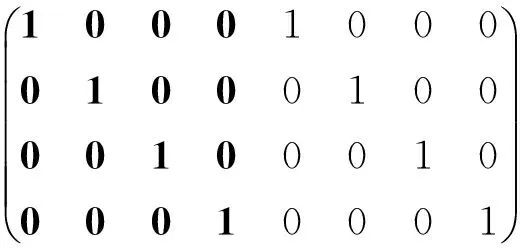
A8的生成矩阵为:

在该生成矩阵中,前四行黑体0和1表示元素全为0和1的1×19行向量。后两行中的U和Vi(i=1,2,3,4)如前所述,后两行前两列中的0表示18×19的零矩阵,后两行后两列的0表示18×1的列向量。
(91,472,15,8,11,23) (75,180,2,3,16,21)
(73,181,0,1,19,23) (39,128,0,2,3,24)
(23,428,3,6,7,6) (29,463,6,16,17,21)
(9,358,15,1,3,15) (9,358,3,17,23,11)
(3,332,13,17,26,17) (3,342,7,7,9,17)
(3,332,8,4,10,22)

111111111111111111100000000000000000000000000000000000000111111111111111111100000000000000000000011111111111111111110000000000000000000000000000000000000010000000000000000000000000000000000000001111111111111111111000000000000000000001011111111111111111100000000000000000000000110110111110010101010101111101010100101111111111111111100000000000000000000000011011011111001110101010111110101000110111111111111111100000000000000000001000001101101111100011010101011111010100111011111111111111100000000000000000000100000110110111110101101010101111101000111101111111111111100000000000000000000010000011011011111010110101010111110100111110111111111111100000000000000000001001000001101101111101011010101011111000111111011111111111100000000000000000001100100000110110111010101101010101111100111111101111111111100000000000000000001110010000011011011101010110101010111100111111110111111111100000000000000000001111001000001101101110101011010101011100111111111011111111100000000000000000001111100100000110110111010101101010101100111111111101111111100000000000000000000111110010000011011111101010110101010100111111111110111111100000000000000000001011111001000001101111110101011010101000111111111111011111100000000000000000001101111100100000110011111010101101010100111111111111101111100000000000000000000110111110010000011101111101010110101000111111111111110111100000000000000000001011011111001000001010111110101011010100111111111111111011100000000000000000001101101111100100000101011111010101101000111111111111111101100000000000000000000110110111110010000010101111101010110100111111111111111110100000000000000000000011011011111001000101010111110101011000000000000000000000001111111111111111111101010111110101010001001111101101100000000000000000000000010111111111111111110110101011111010101000100111110110110000000000000000000000011011111111111111111011010101111101010000010011111011011000000000000000000000011101111111111111110101101010111110101000001001111101101100000000000000000000011110111111111111111010110101011111010100000100111110110100000000000000000000011111011111111111110101011010101111101110000010011111011000000000000000000000011111101111111111111010101101010111110011000001001111101100000000000000000000011111110111111111110101010110101011111101100000100111110100000000000000000000011111111011111111111010101011010101111110110000010011111000000000000000000000011111111101111111111101010101101010111011011000001001111100000000000000000000011111111110111111111110101010110101011101101100000100111100000000000000000000011111111111011111111111010101011010101110110110000010011100000000000000000000011111111111101111111111101010101101010111011011000001001100000000000000000000011111111111110111110111110101010110101111101101100000100100000000000000000000011111111111111011111011111010101011010111110110110000010000000000000000000000011111111111111101110101111101010101101011111011011000001000000000000000000000011111111111111110111010111110101010110001111101101100000100000000000000000000011111111111111111010101011111010101011100111110110110000000
Figure 1 Matrix generated byC1
图1C1的生成矩阵
定理5有19-(4,4)型自同构的二元自对偶码[80,40,16]在等价情况下共有11种。
3.2 p-(c,f)=19-(4,0)
由引理3知,有19-(4,0)型自同构的二元自对偶码[76,38,14],π(Fτ(C))是一个[4,2]码,由文献[1]知,[4,2]二元自对偶码在等价情况只有一种,其生成矩阵为:

同上节,有19-(4,0)型自同构的二元自对偶码[76,38,14]的生成矩阵为:
矩阵中前两行黑体0和1表示元素全为0和1的1×19行向量。后两行中的U和Vi(i=1,2,3,4)如前所述,0表示18×19的零矩阵。
运行Matlab程序,得到:
定理6不存在有19-(4,0)型自同构的二元自对偶码[76,38,14] 。
4 结束语
对纠错码中的二元自对偶码讨论[11],以期找出长度较长的二元自对偶码的生成矩阵及分类。但是,对此类线性码,由于其长度较长和所有型的复杂性,要解决它的分类非常困难。本文中把码长为76、78和80的码分解成长度为4的收缩码和GF(2)n上偶重量多项式的直和,得到了它们的生成矩阵及其分类,并且证明了长度大于80且小于100的二元自对偶码不存在19-(4,f)型的自对偶码。对码长更长的码和不同型的自对偶码,将是作者研究的下阶段目标。这将对解码工作有重要意义。
[1] Huffman W C. On the classification and enumeration of self-dual codes [J].Finite Fields and Their Appplications,2005,11(3):451-490.
[2] Bouyuklieva S, Yankov N, Kim J. Classification of binary self-dual [48,24,10] codes with an automorphism of odd prime order[J].Finite Fields and Their Applications,2012,18(6):1104-1113.
[3] Wang Rong, Wang Jun-xin.[52,26,10] binary self-dual codes with type of (17,3,1)[J].Computer Engineering and Applications,2012,48(19):46-47.(in Chinese)
[4] Wang Rong.Binary self-dual codes with type of 13-(4,m)(m=2,4,6)[J].Computer Engineering,2014,40(11):255-259.(in Chinese)
[5] Yorgov V.Erratum to “The extremal codes of length 42 with automorphism of order 7”[J]. Discrete Mathematics,2011,311(16):1860-1861.
[6] Yang Qing.Binary self-dual codes of length 38[N].Science and Technology Innovation Herald,2011(35):76.(in Chinese)
[7] Fan Ji-qiu,Xie Jing-ran,Yang Qing. Extremal self-dual binary codes with automorphisms with type 3-(12,2)[J].Journal of Jilin University (Science Edition),2008,46(5):870-872.(in Chinese)
[8] Bouyuklieva S, Yankov N, Russeva R. Classification of the binary self-dual [42,21,8] codes having an automorphism of
order 3[J].Finite Fields and Their Applications,2007,13(3):605-615.
[9] Yorgov V Y,Binary self-dual codes with automorphism of odd order[J]. Problems of Inform Transmission,1983(19):11-24.
[10] Lu Zheng-fu,Li Ya-dong,Wang Guo-dong. The further research about the automorphism group of a linear code over GF(2m)[J]. Journal of Yunnan Univeristy(Natural Sciences),2011,23(6):401-404.(in Chinese)
[11] Ning Ping. Exploration for parallel computing of CRC16 checksum on FPGA[J].Computer Engineering & Science,2014,36(6):1023-1027.(in Chinese)
附中文参考文献:
[3] 王荣,王俊新. 有(17,3,1)型的二元自对偶编码[52,26,10][J]. 计算机工程与应用,2012,48(19):46-47.
[4] 王荣. 有13-(4,m)型的二元自对偶码(m=2,4,6)[J]. 计算机工程,2014,40(11):255-259.
[6] 杨庆. 码长为38的二元自对偶极值码[J]. 科技创新导报,2011(35):76.
[7] 樊继秋,谢敬然,杨庆. 具有3-(12,2)型自同构的二元自对偶极值码[J]. 吉林大学学报(理学版),2008,46(5):870-872.
[10] 陆正福,李亚东,王国栋.GF(2m)上线性码自同构群的进一步研究[J].云南大学学报(自然科学版),2011,23(6):401-404.
[11] 宁平. FPGA上实现CRC16纠错编码并行计算的探讨[J]. 计算机工程与科学,2014,36(6):1023-1027.

王荣(1980-),女,山西晋城人,博士,讲师,研究方向为代数编码。E-mail:wangrong101377@126.com
WANG Rong,born in 1980,PhD,lecturer,her research interest includes algebraic coding.

王俊新(1966-),男,山西吕梁人,博士,教授,研究方向为群代数。
WANG Jun-xin,born in 1966,PhD,professor,his research interest includes group alggebra.
Binary self-dual codes with 19-(4,f) automorphism
WANG Rong,WANG Jun-xin
(College of Applied Mathematics,Shanxi University of Finance and Economics,Taiyuan 030006,China )
We discuss the binary self-dual codes of length 76 and 100 with automorphism of order 19. These binary self-dual codes can be seen as a direct sum of contract code of length 4 and some even-weight polynomials overGF(2)n. We prove that self-dual codes of length between 80 and 100 do not exist. We also construct the binary self-dual codes of length 76, 78 and 80 through the shorter self-dual codes respectively, and present their generator matrices. Simulations in Matlab prove that under the condition of equivalence, there are 11 binary self-dual codes of 19-(4, 2) and 19-(4,4) types, whereas binary self-dual codes of 19-(4, 0) type do not exist.
self-dual codes;generator matrix;automorphism;equivalence
1007-130X(2015)09-1661-06
2014-12-17;
2015-04-21基金项目:国家自然科学基金资助项目(70973072,70573066);山西财经大学青年科研基金资助项目(晋财大校[2014]90号)
TN911.22
A
10.3969/j.issn.1007-130X.2015.09.010
通信地址:030006 山西省太原市山西财经大学应用数学学院
Address:College of Applied Mathematics,Shanxi University of Finance and Economics,Taiyuan 030006,Shanxi,P.R.China

