具有自适应趋向性和引导因子的人工蜂群算法*

臧培荃，孙晨骜，顾晓峰，吴 滨，周长喜

(1.轻工过程先进控制教育部重点实验室，江苏 无锡 214122；2.江南大学物联网工程学院，江苏 无锡 214122)

具有自适应趋向性和引导因子的人工蜂群算法*

臧培荃，孙晨骜，顾晓峰，吴 滨，周长喜

(1.轻工过程先进控制教育部重点实验室，江苏 无锡 214122；2.江南大学物联网工程学院，江苏 无锡 214122)

针对人工蜂群算法中存在的收敛速度慢、寻优精度低的问题，提出了一种改进的人工蜂群算法。该算法将自适应趋向性加入雇佣蜂的搜索方案中，同时在观察蜂的搜索方案中加入引导因子。通过雇佣蜂对优秀蜜源的动态趋向搜索以及观察蜂在引导因子引领下的协同搜索，显著提高了算法的局部搜索能力。基于八个标准测试函数的仿真结果表明，与基本人工蜂群算法相比，改进后的算法在寻优精度和收敛速度方面均有明显提升。

人工蜂群算法；局部搜索；搜索方案；自适应趋向性；引导因子

1 引言

Karaboga D[1]于2005年提出的人工蜂群ABC(Artificial Bee Colony)算法是一种模拟蜜蜂采蜜行为的新型群智能算法，具有结构简单、参数设置少及全局寻优能力强等特点，被广泛应用于无约束优化问题[2]。但是，与其他群智能算法一样，传统ABC算法在求解函数优化问题时也存在计算精度低、收敛速度慢、适应范围小等问题。针对这些缺点，不少学者提出了改进方案[3～7]。例如，文献[3]提出在原搜索区域的基础上，根据寻优结果调整搜索空间，缩小搜索区域，并利用混沌变量的内在随机性和遍历性，跳出局部最优，最终获得最优解；文献[4]提出将混沌局部搜索算子嵌入到蜂群算法框架中，以实现在最优食物源周围进行局部搜索，并随着进化代数增加逐步缩小搜索范围，提高局部搜索能力；文献[5]则指出，可利用全局最优解和个体极值的信息来改进人工蜂群算法中的搜索模式，并引入异步变化学习因子，维持全局和局部搜索的平衡；文献[6]利用ABC算法求解单模式资源受限项目调度问题，实现了ABC算法在组合优化中的应用；文献[7]总结了人工蜂群算法解决组合优化问题的框架，并应用于解决旅行商问题TSP(Travelling Salesman Problem)和背包问题。可见，改进ABC算法的局部搜索能力，对提高其性能和扩大其适用范围具有重要意义。本文提出了一种具有自适应趋向性和引导因子的人工蜂群算法ZABC(Zealous Artificial Bee Colony)，有助于提高局部搜索能力，改善算法的寻优精度和收敛速度。

2 人工蜂群算法

ABC算法中将蜜蜂分为雇佣蜂(Employed Bees)、观察蜂(Onlooker Bees)和侦察蜂(Scout Bees)三种类型[8]，蜜蜂寻找优质蜜源的过程就是算法搜寻最优解的过程。其中，蜜源位置代表被优化问题的候选解，蜜源的花蜜量代表相应解的适应度值。求解一个函数f(X)的最小值优化问题的过程如下。

假设初始种群含有M个解(M个蜜源)，每个解Xi(i=1,2,…,M)是一个D维向量，其中f(X)即被优化问题的目标函数。

(1)雇佣蜂负责进行全局搜索：即随机选择蜜源Xi中任意的一维分量按公式(1)进行变异，产生新蜜源Xi′。由贪婪选择机制[9]确定蜜源，即比较前后蜜源的优劣，若新蜜源含蜜量高于旧蜜源，则替换；否则仍保留旧蜜源。

(1)

(2)观察蜂在部分优质蜜源附近作局部搜索：观察蜂根据公式(2)计算蜜源Xi的选择概率Pi，然后针对选中的Xi执行与雇佣蜂相同的变异与选择操作[10]。

(2)

其中，fiti是Xi对应的适应度函数值。

(3)侦察蜂处理进化停滞的蜜源：若某蜜源Xi经过指定的lim次循环后仍未得到改善，则放弃该蜜源，同时由侦察蜂通过公式(3)随机搜索一个新蜜源来代替该蜜源[11]。

Xi=Xmin+φ×(Xmax-Xmin)

(3)

其中，φ为[0,1]的随机数，Xmax和Xmin分别为蜜源解空间的上、下边界。

3 改进的人工蜂群算法

在ABC算法的寻优过程中，雇佣蜂负责全局搜索，观察蜂主要在优质蜜源附近作局部搜索，促使优秀个体逐步向最优位置演化[12]。本文针对雇佣蜂和观察蜂搜索行为中存在的不足进行讨论，并提出改进方案。

3.1 具有自适应趋向性的雇佣蜂搜索模式

ABC算法中，雇佣蜂在蜜源附近按公式(1)随机选择的新方向进行变异，虽然随机方向的选择在一定程度上扩大了搜索空间，但盲目的搜索会导致无效搜索次数的增加，进而降低收敛速度。另外，搜索后期蜜蜂已处于最优蜜源附近，若仍以R×(xij-xkj)大小的随机范围进行搜索，可能导致蜜蜂跃过最优蜜源区域，造成算法搜寻精度不高。

(4)

3.2 具有引导因子的观察蜂搜索模式

ABC算法中，观察蜂在部分优质蜜源附近随机选择一维分量进行局部搜索，搜得的优质蜜源和劣质蜜源是等概率的[13]。然而，只有比原蜜源优秀，新蜜源才会替代原蜜源。因此，50%份额劣质蜜源的引入，将降低算法的寻优精度和收敛速度。

为了提高观察蜂的搜索能力，提出一种具有引导因子的观察蜂搜索方案。具体思路是：选择每只雇佣蜂个体到目前为止搜寻到的最好位置Xp为个体引导因子；选择观察蜂群体到目前为止搜寻到的蜜源中的最优蜜源Xg为整体引导因子。通过引入引导因子，使观察蜂群体内彼此存在着信息交流，避免了孤立个体搜索存在的盲目性大、稳定性差等不足。另外，引导因子本身亦为优质蜜源所处位置，对于观察蜂搜索有较好的方向指引作用，算法收敛速度更快。

观察蜂在随机维度j上的搜索模式如下：

(5)

4 改进的ZABC算法的实验流程

步骤1初始时刻随机生成M个可行解(X1j，X2j，…，XMj)，j∈{1，2，…，D}。设置进化停滞控制参数lim，最大迭代次数tmax和在有利方向最大引导步数Ns的值。

步骤2雇佣蜂在当前蜜源Xi附近根据公式(4)逐维搜索。若新蜜源更优，则对其更新并将该维的搜索方向看作具有引导性的有利方向，沿该方向继续向前搜索，直至适应度值不再改善或达到Ns。

步骤3选择公式(5)的个体引导因子Xp和整体引导因子Xg。

步骤4根据公式(2)计算蜜源被选择的概率Pi，观察蜂在选中的蜜源周围根据公式(5)逐维进行变异和更新。

步骤5侦察蜂检查是否存在连续lim次迭代都没有更新的蜜源，若存在，则由侦察蜂根据公式(3)随机产生一个新的蜜源。

步骤6记录到目前为止的最优蜜源。

步骤7判断是否达到最大迭代次数tmax，若满足，则输出最优蜜源，否则转至步骤2。

5 算法实例测试及分析

5.1 测试函数选择

为了评估本文所提算法的性能，从寻优精度、收敛速度和算法稳定性三个方面对ZABC算法、标准ABC算法和文献[14]提出的改进ABC(Best-so-far ABC)算法进行对比。选用下述八个典型测试函数[15]进行数值实验。

(1)Step函数：

(2)Schwefel’s函数：

(3)Rastrigin函数：

(4)Ackley函数：

(5)Griewank函数：

(6)Rosenbrock函数：

(7)Sphere函数：

(8)Levy函数：

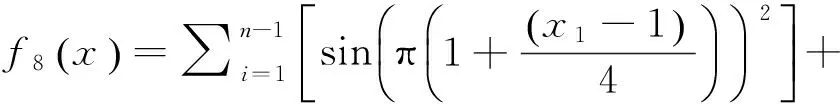
其中，单峰值函数f1、f2、f7的定义域内只有一个极值点，常用来测试算法收敛速度和寻优精度[16]；多峰值函数f3、f4、f5、f8的定义域内有许多局部极值点，常用来测试算法避免早熟和全局寻优的能力；f6为单峰值、非凸、病态函数，较为特殊，函数变量间有很强的关联性，常用来评价优化算法的性能；x*为测试函数的最优解。

5.2 实验结果与分析

实验参数设置为：种群个体数目SN=90，最大进化代数tmax=1 000，最大引导步数Ns=3，进化停滞控制参数lim=100。三种算法均在CPU主频2.4 GHz、内存为2 GB的实验硬件环境下进行测试运行。对比实验中，八个测试函数均在空间维度D=30的情况下分别进行30次独立实验。每个测试函数的最优值、最差值、平均最优值、方差和平均时耗如表1所示。图1～图8给出了八个测试函数的平均适应度进化曲线。

由表1中的最优值、最差值和平均最优值可看出，对于f1和f3，本文提出的ZABC算法收敛达到了理论最优值0；对于其余测试函数，ZABC算法的寻优精度也明显高于另外两种算法。由方差可看出，对于f1，三种算法稳定性相同；对于其他测试函数，ZABC算法方差值有显著的提升，具有更好的稳定性。另外，由平均时耗可看出，ZABC算法达到稳定收敛精度所需的平均运行时间均低于另外两种算法，表明其可以更快地完成寻优过程。

由图1～图8的平均适应度进化曲线可以看出，ZABC算法在单峰函数、多峰函数和非凸病态函数的测试中，达到稳定收敛精度所需的迭代次数远小于另外两种算法，且收敛精度更高。虽然引入自适应趋向性和引导因子一定程度上增加了算法的复杂度和单次迭代的计算量，使算法单次运行时间增大，但由于ZABC算法达到稳定高收敛精度所需的迭代次数更少，使得完成整个搜寻过程的耗时大为减少。这是因为自适应趋向性和引导因子在寻蜜过程中起到了较好的方向指引作用，减少了无效搜索的比重，加快了收敛速度；而搜索步长的动态调整，也在一定程度上减少了搜索后期蜜蜂因跃过最优值而重新搜索的行为，提高了搜索精度，从而获得了更佳的搜索性能。

Table 1 Function test results of the three different ABC algorithms表1 三种不同ABC算法的函数测试结果

Figure 1 Evolution curve of Step function

Figure 2 Evolution curve of Schwefel’s function

Figure 3 Evolution curve of Rastrigin function

Figure 4 Evolution curve of Ackley function

Figure 5 Evolution curve of Griewank function

Figure 6 Evolution curve of Rosenbrock function

Figure 7 Evolution curve of Sphere function

6 结束语

为了解决ABC算法局部搜索能力差、收敛慢、寻优差的问题，针对传统ABC算法中雇佣蜂、观察蜂各自搜索方案的不足，通过在雇佣蜂搜索方案中引入自适应趋向性，在观察蜂搜索方案中加入引导因子，提出了一种改进的人工蜂群算法。基于测试函数的仿真结果表明，提出的ZABC算法具有更快的收敛速度和更高的收敛精度。

[1] Karaboga D. An idea based on honey bee swarm for numerical optimization:Technical Report-TR06[R]. Kayseri: Computer Engineering Department,Engineering Faculty,Erciyes Unversity,2005.

[2] Karaboga D,Basturk B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing,2008,8 (1): 687-697.

[3] Bao Li,Zeng Jian-chao. Self-adapting search space chaos-artificial bee colony algorithm[J]. Application Research of Computers,2010,27(4): 1331-1335.(in Chinese)

[4] Wang Xiang, Li Zhi-yong. Artificial bee colony algorithm based on chaos local search operator[J]. Computer Applications,2012,32(4): 1033-1036.(in Chinese)

[5] Wang Hui-ying,Liu Jian-jun,Wang Quan-zhou. Modified artificial bee colony algorithm for numerical function optimization[J]. Computer Engineering and Applications,2012,48(19): 36-39. (in Chinese)

[6] Akbari R,Zeighami V,Ziarati K. Artificial bee colony for resource constrained project scheduling problem[J]. International Journal of Industrial Engineering Computations,2011,2(1):45-60.

[7] Zheng Wei,Liu Jing,Zeng Jian-chao. The research and application of artificial bee colony algorithm in combinatorial optimization[J]. Journal of Taiyuan University of Science and Technology, 2010,31(6): 467-471.

[8] Bader G D,Donaldson I,Wolting C,et al. BIND-the biomolecular interaction network database[J]. Nucleic Acids Research,2004,31(1): 242-245.

[9] Wang Hui. Artificial bee colony algorithm with sharing factor[J]. Computer Engineering,2011,11(4): 139-142. (in Chinese)

[10] Kang Fei, Li Jun-jie, Ma Zhen-yue. Rosenbrock artificia1 bee colony algorithm for accurate global optimization of numerical functions[J]. Information Sciences,2011,181(16): 3508-353l.

[11] Wang Zhi-gang,Xia Hui-ming. An artificial bee colony algorithm for the vehicle routing problem[J]. Computer Engineering & Science,2014,36(6): 1088-1094.(in Chinese)

[12] Karaboga D,Akay B. A comparative study of artificial bee colony algorithm[J]. Applied Mathematics and Computation,2009,214(1): 108-132.

[13] Ning Ai-ping,Zhang Xue-ying. Convergence analysis of artificial bee colony algorithm[J]. Control and Decision,2013,28(10): 1554-1558.(in Chinese)

[14] Banharnsakun A, Achalakul T, Sirinaovakul B. The best-so-far selection in artificial bee colony a1gorithm[J]. Applied Soft Computing,2011,11(2): 2888-2901.

[15] Zhang Yin-xue,Tian Xue-min,Cao Yu-ping. Artificial bee colony algorithm with modified search strategy[J]. Computer Applications,2012,32(12): 3326-3330.(in Chinese)

[16] Zhao Liang-hui,Wang Tian-qing. A bee colony optimization algorithm for clustering-constraint scheduling[J]. Computer Engineering & Science,2011,33(11): 84-89.(in Chinese)

附中文参考文献:

[3] 暴励,曾建潮. 自适应搜索空间的混沌蜂群算法[J]. 计算机应用研究,2010,27(4):1331-1335.

[4] 王翔,李志勇. 基于混沌局部搜索算子的人工蜂群算法[J]. 计算机应用,2012,32(4):1033-1036.

[5] 王慧颖,刘建军,王全洲. 改进的人工蜂群算法在函数优化问题中的应用[J]. 计算机工程与应用,2012,48(19):36-39.

[7] 郑伟,刘静,曾建潮. 人工蜂群算法及其在组合优化中的应用研究[J]. 太原科技大学学报,2010,31(6):467-471.

[9] 王辉. 一种带共享因子的人工蜂群算法[J]. 计算机工程,2011,11(4):139-142.

[11] 王志刚,夏慧明. 求解车辆路径问题的人工蜂群算法[J]. 计算机工程与科学,2014,36(6):1088-1094.

[13] 宁爱平,张雪英. 人工蜂群算法的收敛性分析[J]. 控制与决策,2013,28(10):1554-1558.

[15] 张银雪,田学民,曹玉苹. 改进搜索策略的人工蜂群算法[J]. 计算机应用,2012,32(12):3326-3330.

[16] 赵良辉,王天擎. 蜂群算法解决集约束调度问题[J]. 计算机工程与科学,2011,33(11):84-89.

臧培荃(1989-),男,山东莱西人，硕士生，研究方向为嵌入式智能研究。E-mail:986025648@qq.com

ZANG Pei-quan,born in 1989,MS candidate,his research interest includes research of embedded intelligence.

孙晨骜(1990-),男，浙江金华人，硕士生，研究方向为嵌入式智能。E-mail:517818554@qq.com

SUN Chen-ao,born in 1990,MS candidate,his research interest includes embedded intelligence.

An artificial bee colony algorithm with adaptive chemotaxis and guiding factors

ZANG Pei-quan,SUN Chen-ao,GU Xiao-feng,WU Bin，ZHOU Chang-xi

(1.Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education,Wuxi 214122;2.School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,China)

We propose an improved artificial bee colony (ABC) algorithm to overcome the drawbacks of slow convergence rate and low optimization precision of the conventional ABC algorithm. The self-adaptive chemotaxis and guiding factors are introduced into the search schemes of employed bees and onlooker bees, respectively. Under the guidance of the guiding factors, the local search capability is significantly improved due to the employed bees’ dynamic search for the high quality nectar sources and the onlooker bees’ cooperative search for the better nectar sources. Simulation results based on the eight standard functions show that the improved ABC algorithm is superior to the conventional one in both computational accuracy and convergence rate.

artificial bee colony algorithm;local search;search scheme;self-adaptive chemotaxis;guiding factor

1007-130X(2015)09-1692-06

2014-09-22;

2014-12-22基金项目：中央高校基本科研业务费专项资金资助项目(JUSRP51323B)；江苏省科技厅产学研联合创新资金资助项目(BY2013015-19)；江苏高校优势学科建设工程资助项目(PAPD)

TP301.6

A

10.3969/j.issn.1007-130X.2015.09.016

通信地址：214122 江苏省无锡市江南大学物联网工程学院

Address:School of IoT Engineering,Jiangnan University,Wuxi 214122,Jiangsu,P.R.China