基于网络搜索数据的住房价格预期与实际价格波动分析

洪 涛，厉 伟

(1.哈尔滨工业大学 经济与管理学院， 黑龙江 哈尔滨 150001；2.河海大学 商学院， 江苏 南京 210098)

【统计应用研究】

基于网络搜索数据的住房价格预期与实际价格波动分析

洪 涛1，厉 伟2

(1.哈尔滨工业大学 经济与管理学院， 黑龙江 哈尔滨 150001；2.河海大学 商学院， 江苏 南京 210098)

在混频数据方法的框架下，分析网络搜索数据是否能够增强中国住房价格的解释能力。对2011年1月至2014年12月的时间序列数据分析显示：以“房价”为关键词得出的百度指数能够解释中国住房价格的部分波动，将其引入传统模型，显著增强了住房价格预测的准确性。研究表明：混频数据方法通过对高频网络搜索数据和低频官方统计数据进行整合，可以挖掘出大数据背后隐藏的丰富信息，为宏观和中观层面的研究提供坚实的微观数据基础。网络搜索数据提供了一个观察个体行为的良好途径，必将在未来促进宏观经济学到纳米经济学的深度融合。

大数据；混频数据方法；百度指数；住房价格

一、引 言

中国住房市场在拉动相关产业和宏观经济发展的同时，也带来了一系列经济、社会问题，因此住房价格的未来走势得到了社会各界的极大关注。从学术研究的角度看，对住房价格的预测大致遵循了两个难以分割的思路。一是将住房价格的决定因素分为经济基础和预期两个部分，前者可以解释均衡价格的变化，后者可以解释实际价格围绕均衡价格的波动。例如，Glaeser认为真实建设成本、抵押贷款利率、居民可支配收入和一月份的温度是重要的决定因素[1]。二是在住房价格核心统计特征稳定不变的假设下，基于历史状况进行预测。通常认为，即使一个城市的住房价格在短期内波动较大，在长期仍然会向其均衡价格回归。例如，Glaeser和Gyourko研究发现，如果某城市住房价格在一个五年周期内超出均衡价格一美元，将会在下一个五年周期内下跌32美分[2]。

对中国住房价格的预测大多散见于报纸、门户网站或社交网络，本质上也契合了国际上的两个学术传统。考虑的因素包括区域经济增长、城市化进程、市场结构、货币供给、居民收入等经济基础因素，也包括对住房价格历史走势的探讨[3]。当然也有一些比较粗糙的指标，如房价收入比。然而，争论的核心往往集中在住房价格泡沫，很少有人谈及泡沫膨胀或破裂的直接驱动因素——预期。原因在于无论是消费者预期，还是生产者预期都取决于微观个体的心理和行为，传统的统计数据难以直接找到合适的代理变量加以度量。

2004年，谷歌公司推出了谷歌趋势指数，即在一段时间内、某个或某类关键词搜索次数占总搜索次数的比例，相比于传统统计数据具有众多良好特性。例如无论在空间层次上、经济分类上，还是在行为特征上都可根据需要进行加总或拆分；通常以周为单位提供数据，具有更好的即时性等等。很多经济学家发现以谷歌趋势指数为代表的网络“大数据”作为微观个体心理和行为的综合度量，可以对很多经济现象进行科学、准确的预测，例如汽车销售、居民消费、旅游到达人数等[4-5]。类似的，利用网络搜索数据对住房市场进行趋势预测近年来也有很快发展。例如，Webb的分析显示以“抵押物拍卖”作为关键词得出的谷歌趋势指数与实际的丧失抵押品赎回权数量之间具有强相关性，可将其作为制定企业战略或政府政策的重要依据[6]。Wu和Brynjolfsson证明，以 “不动产经纪人”和“不动产目录”为关键词的谷歌趋势指数对住房交易量和价格具有显著的解释和预测能力[7]89-118。

本文将百度指数(http://www.index.baidu.com)作为数据来源，利用以“房价”作为关键词得出的百度指数构造反应居民预期的变量，并分析其对住房价格的影响和预测能力。主要创新体现在：提出了利用搜索数据度量居民预期的方法，从传统的间接度量变成了直接度量。利用混频数据方法(简写为MIDAS)整合了高频的搜索数据和低频的住房价格数据，尽可能充分利用搜索数据的即时性所蕴含的丰富信息。

二、模型与数据

(一)MIDAS方法简介

MIDAS方法在统一的分析框架下整合高频数据和低频数据。一方面，保留高频数据频率以充分利用其所蕴含的丰富信息；另一方面，也避免了频率降低所导致的估计无效和有偏问题。由于其所具有的这些优点，MIDAS方法在社会科学分析中有着广泛的应用。假设自变量是高频数据，因变量是低频数据，通常的计量经济模型会采取如下形式：

(1)

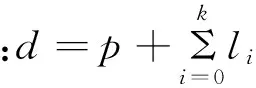
(2)

(3)

其中q为加总形式高频变量在模型中的滞后阶数，并且满足：

(4)

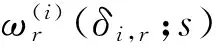
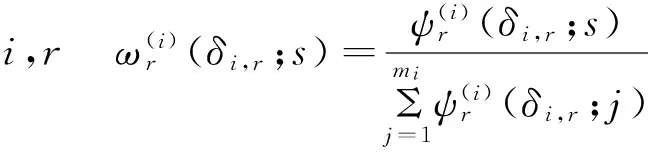
(5)

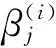
(二)模型设定

消费者的预期形成往往基于历史信息，而非传统经济学上假设的那样完全理性。在一次性外生冲击导致价格上涨的情况下，由于个人特征的差异会产生两种不同的预期。一部分人认为住房价格还会上涨，另一部分人则认为住房价格会下跌，二者均属于行为经济学中所讨论的“小数定理”，即根据小样本去得出所谓规律性的认识。更严重的是，人们对理性行为的偏离具有很强的社会性，即个人并不只是偶尔偏离理性，也不是只有少数人会偏离理性。个人的非理性行为通过群体性错误得到放大，成为左右住房价格走势的重要力量之一。正如Stiglitz所指出的那样：“如果投资者相信未来某种资产能以高于其预期的价格出售时，这种资产的实际价格就会上升”[9]。适应性预期产生的结果是，住房价格并不遵循有效市场中随机游走的假定，而是具有极其显著的序列相关性。这个特征也因此成为了经济学家研究住房市场中预期行为影响的切入点，即利用住房价格的滞后项代表消费者预期，一般性设定形式见式(6)。模型I为：

Δhpt=trend+γΔhpt-1+εt

(6)

其中Δhpt=log(hpt/hpt-1)，hpt为经过季节调整的住房价格，trend为时间趋势，εt为残差。模型I的理论基础是：如果消费者存在适应性预期，住房价格会体现出序列相关性。显然存在几个问题影响论证的严密性。首先是逻辑上的，即使检验出了序列相关性，适应性预期也不必然存在，后者并非前者的必要条件；其次是变量的边界，滞后一期的住房价格包含了过多的信息，用来度量适应性预期显然有范围过宽之嫌；最后是度量的有效性，间接度量没有直接度量更有解释力。

Wu和Brynjolfsson的分析显示，利用搜索数据进行估计，采用简单的线性模型具有更强的解释能力和预测能力[7]。Simon说：“社会科学研究应该追求从具有更高解析度的数据中发现规律，而非为从噪音数据中提取真实信息而盲目的追求更复杂的技术手段”[10]。另外，本文的研究目的是验证搜索数据是否可以作为消费者预期的代理变量，并增加住房价格的预测准确性。基于以上两点判断，本文的基准模型采取了如式(6)的简单线性形式。同时为避免变量自相关对模型估计准确性的影响，在引入搜索数据构建模型II后，放弃了引入更多的控制变量*常用的控制变量如住房抵押贷款利率、住房建设成本、居民可支配收入等都和住房价格的滞后项具有较强的相关关系，也极有可能与消费者的搜索行为具有较强的相关关系。。模型II为：

(7)

已知ΔBt=log(Bt/Bt-1)，Bt是在时期t以“房价”为搜索词得出的百度指数，遵循Guzman利用谷歌趋势指数描述通货膨胀预期时的函数形式，以此来反应住房价格预期。综合模型I和模型II得出模型III为：

(8)

对于模型II和III，采用第二部分介绍的MIDAS方法进行估计。

(三)数据与描述性统计

百度公司在2011年1月开始推出百度指数服务，这决定了本文所用数据时间跨度从2011年1月第1周开始，截止于2014年12月第4周，其中百度指数以周为单位采集。为保证数据结构齐整，假设一个月等于四周。为此需要在一年中删除四周数据，删除的标准是：当月第五周如果超过或等于四天在下一月，则计为下月第一周；如果超过或等于四天位于当月，则予以删除。hpt为商品住宅销售价格，根据国家统计局公布的商品住宅销售额与商品住宅销售面积之商计算得出*数据来源于http://www.stats.gov.cn/。，以月为基本时间单位。原始数据的描述性统计见表1。

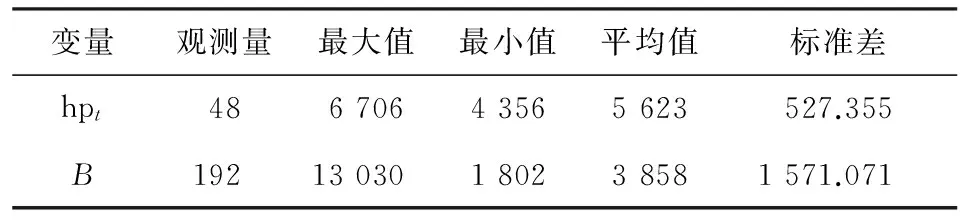
表1 描述性统计指标

图1展示了Δhpt和ΔBt的时间序列，从中似乎无法看出明显相同的变化趋势。然而把百度指数增长率数据推后四周，二者体现出了相当程度的同步变动，这为搜索行为与住房价格的相关性提供了初步证据。

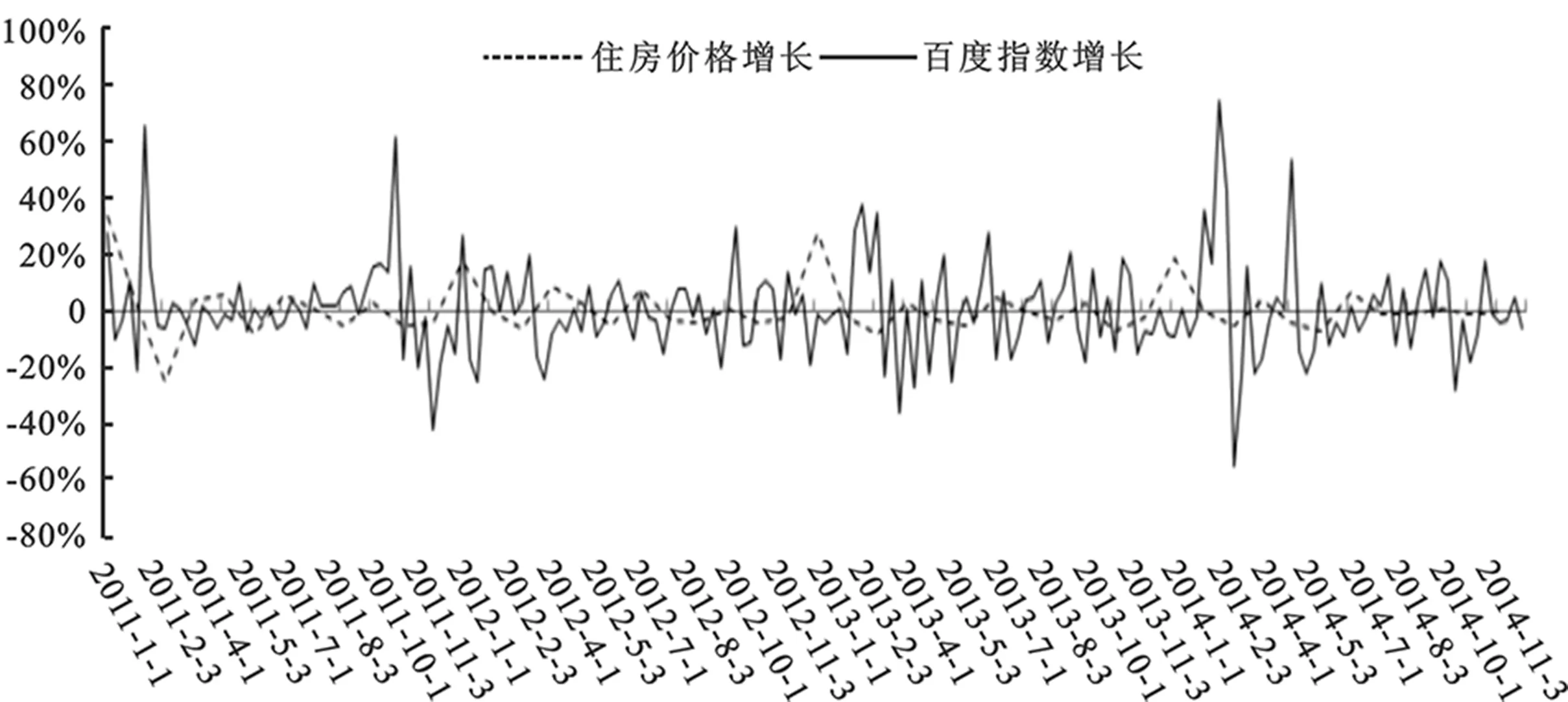
图1 住房价格增加率与百度指数增加率的变化

三、估计结果及预测

(一)估计结果

结合数据特征，本文对模型进行了细化。首先，自变量百度指数增长率是周数据，而因变量住房价格增长率是月度数据，因此模型II-III中的m取值为4。其次，居民的住房消费决策通常比普通消费决策花费周期更长，因此选取百度指数增长率的较长滞后期来对住房价格增长率进行解释。参考部分消费者决策的相关调查，具体数值设定为滞后13周～24周。最后，依据Ghysels等的建议，权重函数采取了式(5)所示的Almon形式，并设r值为2，自变量的待估参数从12个降低为2个[10]。据此，模型II和III具体表示为如下公式。

模型II：

(9)

模型III：

(10)

在式(9)、(10)的基础上，本文还对模型形式进行了若干关键检验。首先，检验了待估参数初始值的合理性。虽然模型I采取了经典的最小二乘方法进行估计，但模型II和III则需要利用非线性方法进行估计，而后者估计结果的合理性对参数初始值设定比较敏感，本文使用了标准的Nelder-Mead代数进行初始值(0.5和-0.1)合理性判断，分别进行了179和253次迭代，结果均达到了收敛，说明初始值设定合理。其次，检验了权重函数形式的合理性。MIDAS方法进行非线性估计的基本思路是获得使残差平方和最小的γi。本文以Almon形式的约束函数为基准，根据非线性估计所产生的参数估计结果，检验了约束函数的梯度及其海萨尼矩阵。结果显示两个模型均拒绝了梯度为零的原假设，且海萨尼矩阵的特征值均为正(具体结果参见表2)，说明权重函数形式设定具有显著的合理性。最后，本文还对高频自变量即百度指数增长率的函数形式及其合理性进行了检验。采用的方法是hAh和hAh-Robust检验，结果显示模型II中hAh和hAh-Robust检验的p值分别为0.334和0.222，模型III中分别为0.350和0.155，说明不能拒绝模型形式设定合理的原假设。

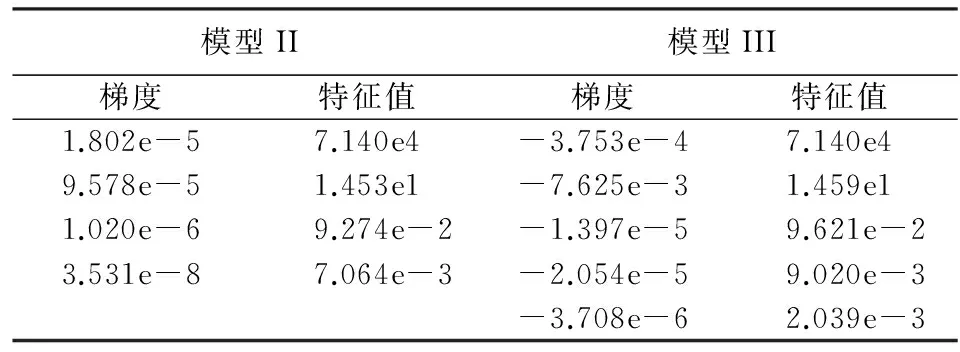
表2 约束函数梯度及海萨尼矩阵特征值

模型I～III的估计结果参见表3。从中可见：第一，模型I的自变量中仅包含因变量的滞后1期，调整R2达到0.972。说明序列相关的特性绝不仅仅是由预期推动而产生的，前期的居民可支配收入、抵押贷款利率等变量对住房价格的影响同样体现其中。由于包含的信息过多，难以从中提炼研究者真正关心的核心要素。第二，模型II中仅包含百度指数增长率作为自变量，两个待估参数均在1%的水平上显著，据此计算出来的滞后13～24周百度指数增长率的系数同样显著为正，说明以搜索指数度量的预期变量对住房价格具有显著的解释能力。第三，模型III在模型I的基础上加入以搜索指数度量的预期变量。即使模型I的调整R2达到0.972，百度指数增长率的估计系数仍然具有较高的显著性，但与模型II相比，无论是从系数估计值还是从显著性上来看均有所下降。

(二)预测

为比较不同模型对住房价格的预测能力，本文将整个样本分为两个阶段：第一阶段为2011年1月至2013年12月，第二阶段为2014年1月至12月。在模型I～III的基础上，利用第一阶段数据得出的参数估计值对第二阶段数据进行预测，并将预测值与实际值进行比较，分析不同模型的预测能力(参见图2)。从中可见，模型I与模型II没有太大差异，分别在不同阶段有更好的表现，而模型III的预测效果显然更好，说明在传统住房价格模型的基础上，添加反应居民预期的搜索指数增长率，能够显著增加住房价格预测的准确性。

表3 模型I～III的估计结果

注：*、**、***分别表示估计结果在10%、5%和1%的水平上显著，括号中数字为标准误。

图2 住房价格增长率的预测值与实际值

表4列出了几个常见的度量预测准确性的指标，同样可以支持从图2中得出的结论，即网络搜索数据和住房价格增长率滞后项对当期住房价格增长率的预测能力相差无几，但在模型I中加入网络搜索数据仍然可以显著提高预测准确性。

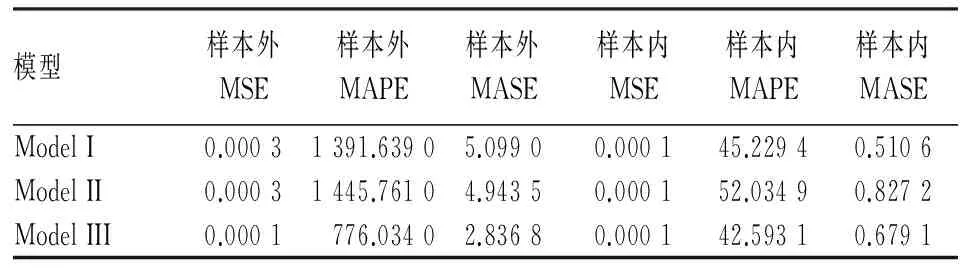
表4 常用预测准确性度量指标

四、结 论

以“房价”为关键词得出的百度指数反应了消费者对住房价格的关注程度，可以将其作为度量预期的变量融入传统模型。本文在MIDAS方法框架下整合高频(周)数据和低频(月)数据，以住房价格增长率的滞后1月和百度指数增长率的滞后13～24周作为自变量构建计量经济模型，并对2011年1月第1周到2014年12月第4周的数据进行分析。结果表明：传统模型利用序列相关特征度量预期，在此基础上引入百度指数增长率可以显著增强模型对住房价格的解释能力。在此基础上，本文将总样本分为两个阶段，利用第一阶段数据进行估计，并以此预测第二阶段的住房价格增长率。百度指数增长率与传统方法具有相似的预测能力，而将其作为新变量引入则可以显著增强模型的预测能力。

现代社会中，网络的普及使虚拟与现实几乎难以划定清晰的界限，人们传统的行为特征几乎全部可以在网络中得以体现。随着技术手段的不断完善，很多以前难以捕捉的微观个体行为以大数据为中介得以数字化和具象化，提供更好的数据支撑和经验研究。这无疑为社会科学研究提供了极好的契机，迅速增加的相关文献数量是最好的证明。本研究证明，网络搜索数据可以用来分析更复杂的经济社会问题，而不应紧紧局限在利用原始数据进行超短期预测。具体到个人和群体行为在住房市场发展中的作用，网络数据同样可以提供有用的微观基础，以得出科学的结论。由此可以预测，未来的经济学必然有一部分是沿着纳米经济学到宏观经济学的脉络发展的。

[1] Glaeser E L. Housing Prices in the Three Americas [N]. New York Times， 2008-09-30.

[2] Glaeser E L，Gyourko J. Housing Dynamics[EB/OL].[2006-12-19].http://www.nber.org/papers/w12787.

[3] 原鹏飞，邓嫦琼.住房价格上涨与其影响因素之间的关系研究——基于VEC模型的实证分析[J].统计与信息论坛， 2008，23(11).

[4] Carrière-Swallow Y，Labbé F. Nowcasting with Google Trends in An Emerging Market [J]. Journal of Forecasting， 2013, 32(4).

[5] Choi H， Varian H A L. Predicting the Present with Google Trends [J]. Economic Record，2012, 88(1).

[6] Webb G K. Internet Search Statistics as A Source of Business Intelligence: Searches on Foreclosure as An Estimate of Actual Home Foreclosures [J]. Issues in Information Systems， 2009, 10(2).

[7] Wu L， Brynjolfsson E. The Future of Prediction: How Google Searches Foreshadow Housing Prices and Sales [M]∥ Goldfarb A, Greenstein S，Tucker C. Economic Analysis of the Digital Economy. Chicago: University of Chicago Press， 2015.

[8] Ghysels E, Sinko A，Valkanov R. MIDAS Regressions: Further Results and New Directions [J]. Econometric Reviews， 2007, 26(1).

[9] Stiglitz J E. Financial Markets and Development [J]. Oxford Review of Economic Policy, 1989, 5(4).

[10]Simon H A. On the Behavioral and Rational Foundations of Economic Dynamics [J]. Journal of Economic Behavior & Organization，1984, 5(1).

(责任编辑：李 勤)

A Study on the Relationship Between Expectation and Real Housing Prices Based on Query Index

HONG Tao1, LI Wei2

(1. School of Economics and Management, Harbin Institute of Technology, Harbin 150001,China;2. Business School, Hohai University, Nanjing 210098, China)

Based on MIDAS approach and time series data from January, 2011 to December, 2014, this paper focuses on whether query indices can improve the forecasting performance of housing price or not. Empirical analysis comes to the conclusion that Baidu index could explain parts of fluctuation of housing prices and improve the forecasting performance by introduce it into traditional models. It could dig out more information behind big data that MIDAS approach combines high and low frequency data, and then construct micro foundation for macro-and meso-analysis. Query index could be a solution to unite macroeconomics and nanoeconomics.

big data； MIDAS approach； Baidu index； housing prices

2015-07-10

国家自然科学基金项目《S-C-P 范式下中国住房市场波动的冲击-传导机制分析》( 71103051)

洪 涛，男，黑龙江哈尔滨人，经济学博士，副教授，研究方向：城市发展管理； 厉 伟，男，江苏淮安人，管理学博士，教授，研究方向：不动产经济学。

F222.3

A

1007-3116(2015)11-0049-05