基于联合正则化的稀疏磁共振图像重构

葛岭岭，张志伟，张婷婷

（河北工业大学 电子信息工程学院 天津 300401）

压缩感知[1]（CS）是Donoho和Candes等提出的一种新兴的信号获取与处理理论。如果图像在某个变换域可以稀疏表示，那么我们可以通过求解相关的优化问题，就可由随机下采样的稀疏系数来进行重构，并在一定程度上保持原有图像的重构质量。基于压缩传感的MRI重建算法利用MRI稀疏表示或局部光滑的先验知识,通过求解相应的优化问题来实现重建。目前已有多种算法解决此类优化问题。SL0算法（smooth L0 norm）[2]利用图像在小波变换域具有稀疏性的特点，可以将L0范数最小化问题转化为近似L0范数的最小化问题，有效解决了L0范数优化中的NP难问题，这类算法基于凸优化的迭代算法，姑且可以成为另类的压缩感知算法，这种算法的主要特点就是估计精度高而且计算量很低，而且对于信噪比变化不是很敏感，因此可以获得稳健的稀疏估计量。 文献[3]中 Bhaskar提出当（0＜P＜1）时基于 LP范数的迭代加权最小二乘 （Iteratively Reweighted Least Square,IRLS）算法，实验证明了基于LP范数的优化算法无论是在信号重建效果，还是在可靠性方面都优于L1及L0范数优化算法，Bioucas－Dias等 提 出 TVMM （Total variation based majorization minimization）算法[4]，该算法利用图像局部光滑特性，采用全变分正则化重建图像。上述算法均采用单一的正则项来重构图像，重构出的效果都不是很理想，针对这一问题，本文利用联合正则化的原理以及压缩传感理论 ,提出一种基于压缩传感的联合正则化MRI图像重建算法。

1 基于压缩感知的MRI重构

1.1 MRI图像重构的模型

Candes[5]等人证明了图像重建问题可以通过求解一个最小L0范数的问题加以解决。但是L0问题为NP组合难问题，对较大规模数据无法直接求解，针对这一问题,研究者们提出了一系列寻找次优解的贪婪算法：匹配追踪MP（Matching Pursuit）算法[6]，正交匹配追踪 OMP（Orthogonal Matching Pursuit）算法[7]等。但是贪婪算法时间代价过高，无法保证收敛到全局最优。当前一般性的作法是将L0范数最小化问题放松到L1范数最小化问题，从而将一个组合优化问题放松到一个凸优化问题来求解。即：

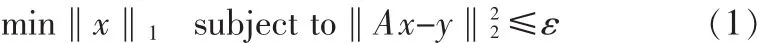
研究中发现：L1求解框架不能保证获得满意的稀疏解，它往往与真实稀疏解（L0的解）差距甚大[8]。并且当采样数逐渐减少时，L1求解框架重构效果不理想，对于含有重尾分布的误差数据往往不能取得好的效果，重构的图像也不稳定。因此一个自然改进方法是使用 Lq框架（0＜q＜1），本文根据徐宗本[9]院士的基本思想，研究一种改进的图像重构模型，惩罚项中将L1换成L1/2，如此MRI图像小波变换域稀疏性就可以通过图像小波变换系数L1/2的范数的大小来衡量，图像的局部光滑特性可以用全变差（Totalvariation，TV）的大小来衡量。

MRI图像重构就可以通过求解下列优化问题来实现：

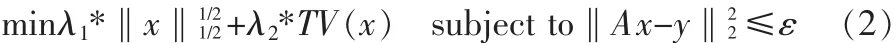
其中 λ1，λ2为权重参数。

1.2 改进模型求解

利用拉格朗日原理将式（2）约束优化问题转换为无约束优化问题，并引入辅助变量 u，v，问题（2）可以转换为求解等式约束优化问题，

再次利用Lagrange定理将（3）式转化为无约束优化问题

根据交替方向乘子法 （Alternating Direction Method of Multipliers，ADMM）[10]，采用交替最小化思想，其求解过程如下

更新x时

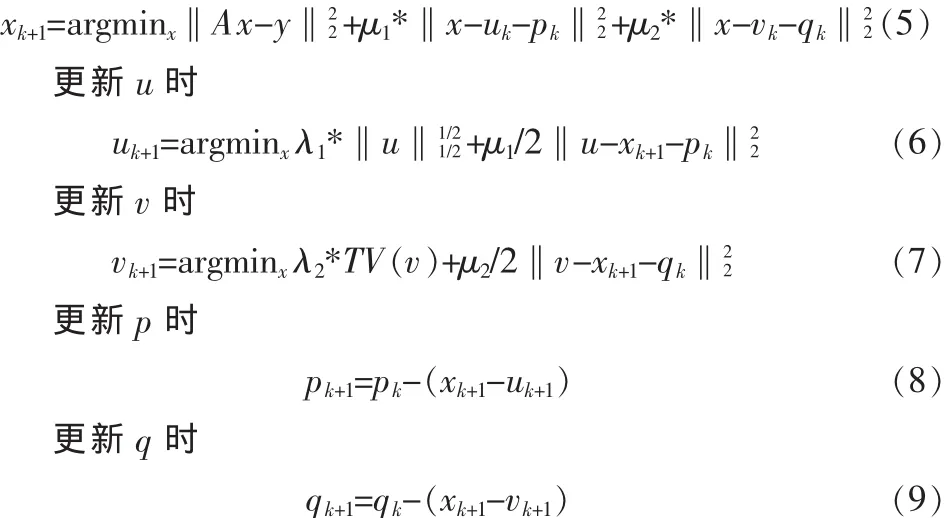
如果式（5）、（6）和（7）有准确解，根据 Eckstein－Bertsekas定理可保证此算法的收敛性。式（5）是一个强凸函数，其最小化可以写成如下形式：

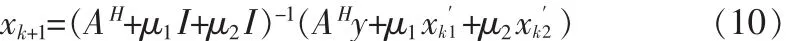
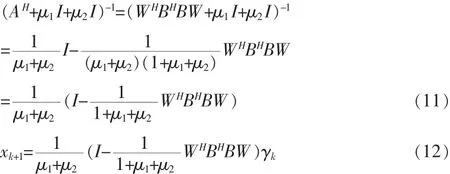
这里的 φ（x）=λ1*‖u‖+λ2*TV（v），根据 Eckstein－Bertsekas定理，若误差的序列是可求和的，那么也可保证算法的收敛性，这里TV范数和L1/2范数正则项的去噪问题可以使用Chambolle解法进行求解。

2 结果与分析

2.1 评价标准

为验证本文方法的有效性，采用Shepp－Logan脑部模型的磁共振图像进行验证，由于非笛卡尔采样具有采样速度快、对流动不敏感等优点，它在脑功能成像、心脏冠状动脉成像等方面得到了人们的关注，本文采用非笛卡尔辐射状采样，在脑部模型的Fourier频谱表示图上，均匀取L条射线，然后在每条射线上高斯采样。利用CPU为2.0 GHz，内存为2G的计算机，通过MATLAB进行编码。本文分别通过MSE、SNR、PSNR 3个参数对改进的模型与正则项分别是L1范数，TV范数的模型进行分析比较。

2.2 不同正则化的比较

将正则项分别是L1/2范数、TV范数与联合L1/2范数和TV范数的实验结果进行比较，这里实验结果如表1所示，运用三种方法，在不用分辨率与采样数的情况下，计算出原始图像和重建图像的相对误差，以及算法的迭代数和运行时间。从仿真结果表1中可以看出，在分辨率为64*64，采样数为52时，联合正则化的差错率为2.26e－007，到达了一个非常理想的效果，L1/2范数的差错率为2.72e－007，而TV范数的差错率为4.56e－007，所以我们得出在分辨率较低时，联合L1/2范数和TV范数的重构效果要比单一正则项的重构效果好。可是分辨率虽然有所提高，我们看到无论是重构时间还是迭代次数相对于L1/2和TV范数都提高了很多，分辨率为32*32，采样数为22时，L1/2范数重构时间为9.40 s，TV范数重构时间为4.61 s，联合正则化的重构时间为71.71 s，是L1/2和TV范数的将近十倍。而在分辨率达到256*256时，L1/2范数的差错率为1.99e－007，TV范数的差错率为2.07e－007，而联合正则化的差错率为6.02e－007，低于单一正则项时的差错率。

图1给出了在分辨率为32*32时，联合正则化和单一正则化的差错率的对比图，通过图中们可以看出，在采样数不断增加的情况下，联合正则化的差错率要低于单一正则项时的差错率，当采样数达到52时，联合正则项的准确度比单一的TV范数正则项时高出0.5个百分点，说明联合正则化重构出的图像更接近于原始图像。

表1 不同正则化方法随不同采样数的图像恢复结果Tab.1 Image restoration results with different regularization

图1 不同正则化的差错率对比（128*128）Fig.1 Error rate comparison

图2是分辨率为128*128时，联合正则化和单一正则化恢复的PANR以及SNR的对比分析，联合正则化的PSNR比单一正则化的PSNR略微有所降低，但是重构出效果仍然比较理想，随着采样数的增加，联合正则化的SNR逐渐接近单一正则化的SNR。

图2 PSNR与SNR的对比Fig.2 Comparison of PSNR and SNR

图3 原始图像Fig.3 Original image

图4 重构图像Fig.4 Reconstructed image

图3 是MRIscan图像的原始图像，图4是在采样数为52的情况下利用联合正则化的模型的重构结果，联合正则化模型重构的差错率是6.002e-007，从图中可以看出，改进方法的重构结果十分接近原始图像，证明了该方法的有效性。

3 结 论

本文针对MRI图像重构研究了一种图像重构的新方法，联合正则化模型能够很好的重建稀疏的磁共振图像，并且数据试验证明在分辨率较低采样数较少的情况下，联合正则化的重建效果要高于单一正则化，能够达到比较理想的效果，但是该模型还是有不足之处，就是重构时间比较长，迭代次数也较单一正则化较多，在运行时间方面需要改进，不过瑕不掩瑜，实验结果证明了该模型的成立。

[1]E Candes.Compressive sampling.Proceedings of the International Congress of Mathematicians[J].Madrid， Spain，2006（3）:1433-1452.

[2]Peng X，Zhang M，Zhang J，et al.An alternative recovery algorithm based on SL0 for multiband signal[C]//Instrumentation and Measurement Technology Conference（I2MTC）， 2013 IEEEInternational.IEEE，2013:114-117.

[3]Bhaskar D.Rao，Kenneth Kreutz-Delgado.An affine scaling methodology for best basis selection[J].IEEE Transactions on Signal Processing，1999，47（1）:187-200.

[4]Bioucas-Dias J M，Figueiredo M A T，Oliveira J P.Total variation based image deconvolution: a majorization minimization approach [J].IEEE Conference， Toulouse，2006（2）:278-281.

[5]E.J.Candes， J.Romberg， T.Tao.Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information [J].IEEE Transaction on Information Theory，2006，52（2）:489-509.

[6]S.G.Mallat，Z.Zhang.Matching Pursuits with Time-frequency Dictionaries[J].IEEE Transactions on Signal Processing，1993:3397-3415.

[7]Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory，2007，53（12）:4655-4666.

[8]E.J.Candes，M.Wakin.An Introduction to Compressive Sampling[J].IEEE Signal Processing Magazine，2008，25（2）:21-30.

[9]XU Zong-ben，CHANG Xiang-yu，XU Feng-min.L-1/2 Regularization:A Thresholding Representation Theory and a Fast Solver[J].IEEE Transactions on neural net-works and Learning Systems，2012，23（7）:1013-1027.

[10]Stephen Boyd，Neal Parikh，et al.Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers [J].Foundation and Trends in Machine Learning，2010，3（1）:1-122.