一种基于信息素和信息熵的蚁群聚类算法

王 慧， 甘 泉

（1.平顶山学院 招生就业处，河南 平顶山 467000；2.平顶山学院 计算机与科学技术学院，河南 平顶山 467000）

数据挖掘技术领域中的数据聚类的存在，是对事物进行了解的重要步骤。20世纪90年代，Dario M等人提出了蚁群算法[1]，最早被用于解决旅游商问题，还用于二度调度问题[2]。随着蚁群算法的广泛应用[3]，人们发现蚁群模型在某些方面更接近实际的聚类问题。在与其他聚类分析模型进行比较时，基于蚁群的聚类分析模型有较多的优点：这种模型一般是独自需要解决相关难题，会自动根据数据对象的特征产生聚类的数量，会更好地处理噪声和异常值[4]，会处理不同维度的数据集，能较容易完成数据的可视化。

1 蚁群聚类基本原理

Lumer和Faieta[5]对基本模型进行了扩展，在数据分析领域广泛应用，提出了LF算法。该算法先将数据任意散放在单独网格里，在地点蚂蚁能有效的感受到周围的状况。对象Oi在地点r与附近事物的相似度由下面公式计算[6]：

其中，f（Oi）表示对象Oi和其邻域内的对象Oj之间的相似度的度量[7]。参数a代表了相差异的度量，利用它来确定两个数据对象能否放置在一起。Neighs′s是指以地点r为中心的的区域s′s。 在LF算法中蚂蚁拾起或者放下一个对象Oi的概率分别按照以下公式计算：

公式中Pp表示蚂蚁拾起对象Oi的概率，Pd表示蚂蚁放下对象Oi的概率，k+和k－是两个常量。

2 基于信息素和信息熵的蚁群聚类算法（ALFBP）

在LF算法中，基本模型被扩展到了数据分析范畴，而且有很大的进展，由于这种算法的参数设置繁琐，并且敏感，同时对于运动的区域进行了限制，即二维网格的圈定，对于某些网格的存在失去了意义，例如没有数据的网格。所以，这种“物以类聚”统计分析情况并不尽如人意。改进算法思想为：首先将有需要的数据对象分布于二维网格，然后具体的具有蚂蚁真实的群体行为进行聚类剖析。采用信息素和短期记忆的思想对控制蚂蚁的随意移动进行控制，把信息熵作为蚂蚁运动状态的转换规则，信息熵的计算与比较来替代LF算法中的群体相似度计算和概率转换函数，对拾起和放下数据对象的判断规则进行修改。实验结果显示证明了改进算法是有效的，算法取得了较好的聚类结果。

2.1 蚂蚁空间转移策略

在一个二维的平面网格中，蚂蚁的短期记忆[8]和网格中信息素的分布决定了蚂蚁从一个位置到下一个位置的空间转移.相应的解决方法为：让每一个蚂蚁都能够记住近几次所放下的数据对象和相应的位置，如果新的数据对象被拾起，分析新对象与某个数据对象之间的关系，看是否可以归并，如果不能，可以按照具体的数据分布来确定下一步的移动方向[9]。假设蚂蚁在平面网格上的具体位置为（γ，θ），在它的走过的痕迹中会留下相应的信息素，在步长时间段内，所留下的信息为η，伴随时间的推移，推移过后的信息就会进行相应的减少，设减少的衰减率为κ。那么蚂蚁从k转移到位置i的空间方面的转移概率pik用以下公式来确定[9]：

W（si）响应函数（response function）是关于 i的信息 素（pheromones）浓度所表示的，证明膜翅目昆虫在关于信息素（pheromones）浓度为σi的位置i的相对出现率，较高的β取值使膜翅目昆虫顺着信息素的有关方向位移，其中β是决定膜翅目昆虫所有情况的抗噪比相关的参数数据，1/δ证明膜翅目昆虫在具有信息素（pheromones）范围内所能捕捉到信息素改变之能力，j/k表示在k邻域内所有网格单元j的和，集合中的参数β与1/δ二者是形成了信息素（pheromones）痕迹的关键因素。w（Di）为到位置i的权值因素，Di代表在时间为步长的时候的位置i与位置k在方向方面的区别量，依据Di的值来对w（Di）进行确定[10]，膜翅目昆虫的移动方向能够事先看成为如图1中的情况，因为各方格有8个紧挨着的网状式单元组成，也就有8个不同的方向进行移动，产生8个方向，各个方向之间的夹角为45°，那么膜翅目昆虫可事先从此8个方向当中，任意选取1个方向，则膜翅目昆虫迅速的改变方向的概率远远小于缓慢的改变方向的概率[9]，所以，定义相异改变度数之数值与文献[11]相同分别为：w（0°）=1，w（±45°）=0.5，w（±90°）=0.25，w（±135°）=0.08，w（180°）=0.05。

2.2 信息熵的计算

信息熵是一个比较抽象的数学概念，把信息熵定义为离散型随机事件产生的概率。学者Shannon（香农）对信源符号熵的界定[12]如下：假定随机变数为X，存在取值集是x，就具有一定的可能性，在为x值的情况下，则可能性的函数就为p（x），信源符号熵E（x）的相关公式是：

针对 1 个数项变量之矢量 x=（x1，x2，…，xn）的信息熵的计算公式为：

其中 p（x1，x2，…，xn）是多变量可能分布函数，X1，X2，…，Xn是相应向量项的可能取值集合。

通过借用信息熵中包含聚类的子空间的信息熵比不包含聚类的信息熵小的特征，在LF算法中引入信息熵 ，对数据对象拾起和放下的判断规则进行更改，设置的参数变少了，取得了较好的聚类质量。该策略描述为：单个负重oi对象的膜翅目昆虫位移至网络中空白区，运算附近s′s范围里的对象信源符号熵，试想未放下对象oi前的信源符号熵在与该区域的信源符号熵进行比对时，前者略大于后者，则放下该对象oi单个并未负重的膜翅目昆虫移至对象oi处，计算附近s′s区域中的对象信息熵，试想oi未拾起对象前的信源符号熵与该对象后该范围的信源符号熵，在做出对比时，前者大于后者时，不小于拾起则拾起对象oi。假定所有 “数据对象”（Data Object）包含 n个属性，且它们之间是独立的关系，A1，A2，…An，每个属性之取值集为 X1，X2，…Xn，就有极大的可能性 s′s区域中的对象信息熵E（s2）为：

2.3 算法描述

据上面对基于信息素和信息熵的蚁群聚类算法的讨论，ALFBP算法的过程如图2所示。

在ALFBP算法中，影响蚂蚁运动状态的因素仅有邻域s参数，比LF算法里的设置参数不多，在各次放下对象的时候，可以不增多非大块范围之信源符号熵，拾起的时候，可以不减少非大块范围的信源符号熵，还能加快聚类过程，达到好的聚类结果。通过多次的仿真实验，当形成一些较小的聚类时，负载的蚂蚁会很多次寻找放下的位置，就会多次出现E1＜E2的情况，导致不能放下拾起的数据.在较长迭代过程中，这些蚂蚁起不到聚类的作用。为了防止这种情况的产生，使蚂蚁在放下数据的失败次数达到一定值时（取100次），强行放下数据，加速了聚类的进程。

3 仿真实验分析

1）为了测试ALFBP算法的聚类质量和改进算法的有效性，分别进行了两组各十次实验，比较了最终聚类结果与LF算法的聚类结果。算法采用JAVA来实现。实验使用UCI公共数据库所提供的两个数据集（表1），这两个数据集都有自己的分类表，能够评价最终的聚类性能，设置算法的参数参见（表2）。聚类性能评价通过计算F－measure的值，最大迭代次数都设置为106。

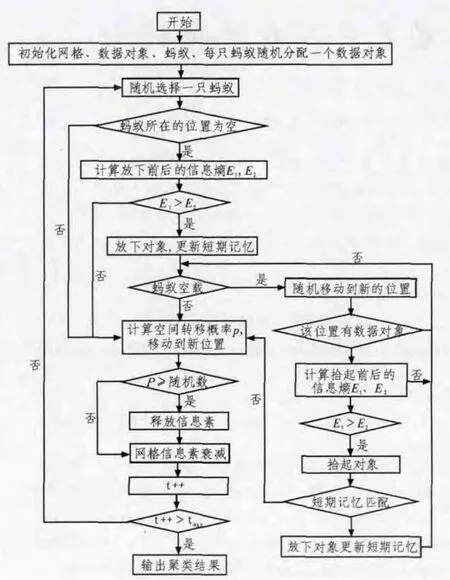
图1 ALFBP算法流程图Fig.1 ALFBPalgorithm flow chart

表1 实验数据集表示Tab.1 Experimental data set represents

表2 实验参数表Tab.2 Experimental parameters table

第一组实验中，使用Iris数据集来测试算法的聚类质量。在20次实验中，ALFBP算法的F－measure值有18次超过了LF算法的F－measure值。就平均 F－measure值而言，ALFBP算法达到了0.945，LF算法为0.889。由此可知，聚类质量ALFBP算法要优于LF算法。而且，对比LF算法，ALFBP算法避免产生小块的聚类。

第二组20次实验中，采用了数据集Zoo来测试算法的聚类质量。在20次实验中，ALFBP算法的F－measure值全都超过了 LF算法的 F－measure值。ALFBP算法平均 F－measure值为0.856，能够保持比较满意的聚类效果，但是LF算法之平均数值约是0.688，聚类之效果并不明显[16]。由此可见ALFBP算法更适合于高纬数据的处理。

2）正态分布测试数据集。数据集中的4组数据的属性按照正态分布产生，每组200个数据，各组数据服从均值为μ，方差为s=2的正态分布。

具 体 为 ： 类 1 为{x～N[0，2]}，{y～N[0，2]}， 类 2 为 {x～N[0，2]}，{y～N[8，2]}，类 3 为{x～N[8，2]}，{y～N[0，2]}，类 4 为{x～N[8，2]}，{y～N[8，2]}。 数据集随机的分布在 60×60 的网格上，蚂蚁速度限制在1到10之间。邻域大小为3，蚁群大小为20，分别用LF算法和ALFBP算法对生成的数据集进行聚类，经过16万次的迭代得到误差函数随迭代次数的变化曲线图如下：

图2 两种算法误差比较Fig.2 Comparison of the two algorithms error

在图2中，横坐标为表示为迭代次数104，纵坐标表示为误差平方和102。从图2可以看出ALFBP算法有较好的收敛性能，而且能够加快聚类，这是因为ALFBP算法设置的参数减少了，使用ILFBP算法中定义的蚂蚁信息素和短期记忆方式校正其随机移动，利用信息熵作为蚂蚁运动状态转换规则，每次对于数据的拾起和放下都会对区域的信息熵有减少或者增加的影响。还能加快聚类过程，使相似度大的数据对象能够较快地聚集在一起能够加快聚类。另外，2种算法经过16万次迭代后的 F－measure值为LF为0.234 4，ALFBP算法为0.982 2，这些结果都表明该算法可行。

4 结 论

文中在蚁群聚类模型中，引入了信息熵和信息素，提出了基于信息素和信息熵的蚁群聚类分析算法，并设计和实现了一个简单的蚁群聚类分析平台，通过测试数据集对改进的算法进行分析，算法显示出了较高的稳定性和准确率，证明了该改进算法的有效性。

[1]Dorigo M，Bonabeau E，Theraulaz G.Ant algorithms and stigmergy[J].Future Generation Computer Systems，2000，16（8）:851-871.

[2]宋佩莉，祁飞，张鹏.混合蚁群蜂群算法在旅行Agent问题中的应用[J].计算机工程与应用，2012，48（36）:33-38.SONGPei-li，QI Fei，ZHANG Peng.Hybrid ant colony colony algorithm in travel agent probl[J].Computer Engineering and Applications，2012，48（36）:33-38.

[3]侯超，侯永.一种改进蚁群聚类算法在数据挖掘中的研究[J].微计算机信息，2011，27（12）:136-138.HOU Chao，HOU Yong.An ant colony clustering algorithm in data mining[J].Micro Computer Information，2011，27（12）:136-138.

[4]宋中山，周腾，周晶平.一种改进的蚁群聚类算法在客户细分中的应用[J].计算机应用研究，2013，32（3）:77-81.SONG Zhong-shan，ZHOU Teng，ZHOU Jing-ping.An improved ant colony clustering algorithm in customer segmentation[J].Application Research of Computers，2013，32（3）:77-81.

[5]Lamer E，Fajita B.Diversity and adaptation in populations of clustering ants[C]//Cliff D，Husbands P，Meyer J，et al.From Animals to Animates 3.Proc of Third International Conference on Simulation of Adaptive Behavior.Cambridge，MA，USA:MIT Press，1994:501-508.

[6]张斌.蚁群聚类算法在WEB使用挖掘中的应用研究[D].南宁：广西大学，2007.

[7]许智超.基于蚂蚁系统的基因表达数据聚类分析 [D].福州：福建农林大学：2012.

[8]M Dorigo，L M Gambardella.Ant colony system:a cooperative learning approach to the traveling salesman problem[J].IEEE Transactions onEvolutionary Computation，1997，1（1）:53-66.

[9]王慧.改进的蚁群聚类分析算法的研究[D].开封：河南大学，2009.

[10]D R Chialvo，M M Millonas.How swarms build cognitive maps[C]//In:Luc Steels ed.The Biology and Technology of Intelligent Autonomous Agents， Nato ASI Series，1995:439-450.

[11]V Ramos，F Muge，P Pina.Self-Organized Data and Image Retrieval as a Consequence of Inter-Dynamic Synergistic Relationships in Artificial Ant Colonies[C]//Inn'：J Ruizdel-Solar， A Abraham， M koppen Eds.Hybrid Intelligent Systems， Frontiers of Artificial Intelligence and Applications， Santiago， Chile， 2002.

[12]许国志，顾基发，车宏安著.系统科学[M].上海：上海教育出版社，2000.