利用复合型冲突表示的快速加权证据融合方法*

白东颖，王刚，李松，姚小强

（1.第二炮兵工程大学，西安710025；2.空军工程大学防空反导学院，西安710051）

利用复合型冲突表示的快速加权证据融合方法*

白东颖1，2，王刚2，李松2，姚小强2

（1.第二炮兵工程大学，西安710025；2.空军工程大学防空反导学院，西安710051）

针对经典D-S证据理论在处理大规模冲突证据组合时的悖论问题及计算量指数增长问题，提出了一种利用经典冲突系数与证据距离共同度量冲突大小的快速加权融合方法。该方法通过分析单一冲突表示方法的不足，提出了复合冲突系数，同时，给出了证据中心及当前中心距离的定义，并用当前中心距离与冲突系数一起确定证据权重。算例实验结果表明本算法有效地解决了经典证据理论中的悖论问题并显著地提高了融合速度。

证据理论，冲突系数，证据中心，中心距离

0 引言

D-S证据理论［1-2］作为一种不确定性推理方法，通过引入信任函数，区分了不确定与不知道的差异，在多源信息融合中具有广泛的应用。然而，D-S理论在对高冲突证据组合时，会出现有悖人类直觉的结论［3-4］。国内外学者提出的改进方法总的来说可以分为3类：修改传统证据理论模型框架、修改证据组合规则、修改证据源模型。

修改证据源模型的代表人物是Murphy［5］和Haenni［6］。他们认为修改证据源方法较之于修改模型框架及组合规则更为合理。因此，本文从修改证据源角度来处理D-S规则组合时的悖论问题。证据源修正最具代表性的是Murphy平均法，但该方法并未考虑各个证据之间的关联。

在Murphy基础上，依据各种方法来量化证据间的冲突进而获得证据可信度作为修改证据源的权重指标是多数改进方法的思路［7-9］，但这些方法仅从单一角度对冲突进行表示，有时会出现“死角”现象；同时，衡量冲突往往需要用证据间距离进行相似性度量［10-11］，当证据规模较大时，会出现计算量指数增长。

基于以上两方面问题，本文尝试利用经典证据理论中的冲突系数［1］与证据距离［12］共同度量冲突大小，进而获取证据权重，用修改后的证据源进行合成。同时提出，用中心距离代替两两证据距离，缩短大规模证据融合时的计算量。

1 D-S证据理论及典型悖论问题

1.1 Dempster-Shafer组合规则［2］

设Θ为一识别框架，则函数m：2Θ→［0，1］满足以下条件①m（φ）=0；②0≤m（A）≤1；③=1；则称m为识别框架Θ上的基本置信分配（Basic Belief Assignment，BBA）函数。

定义1：设m1（·）和m2（·）是2Θ上的两个相互独立的BBA（基本概率分配函数），定义组合后的BBA：m（·）=［m1⊕m2］（·）为

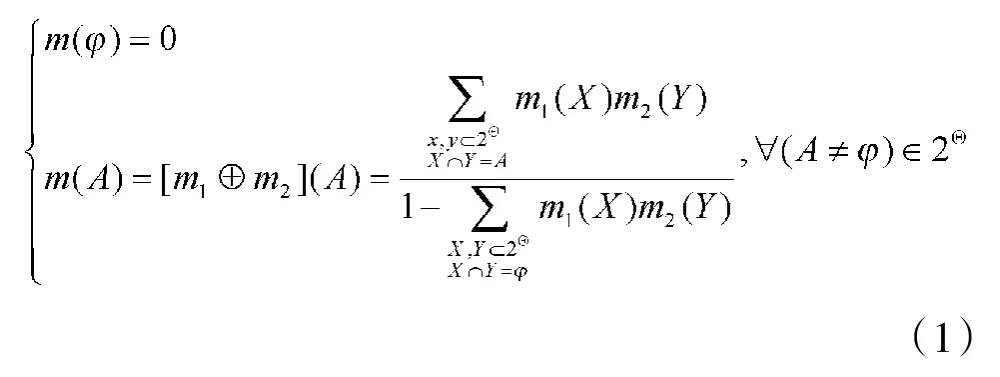
式（1）中，⊕为直和运算，也称正交和（orthogonal）运算。

1.2 Zadeh悖论［13］

例1：设识别框架Θ={A，B，C}，BBA分别为：

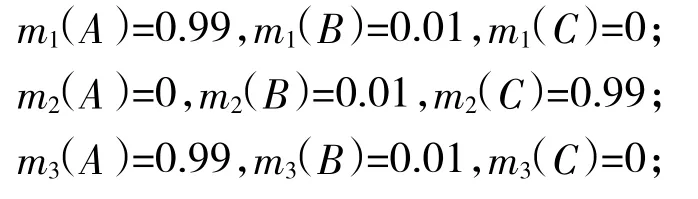
用D-S组合规则合成结果：m12（A）=0，m12（B）=1，k=0.999 9，无论后续证据如何支持某一焦元，结果始终为m（A）=m（C）=0，m（B）=1。小概率事件m（B）经过融合结果变为必然事件。该结果有悖于人类直觉。

1.3 信任偏移悖论［14］

例2：设识别框架Θ={θ1，θ2，…，θn}，BBA为m1（θ1）=0.06，m1（Θ）=0.94，mi（θ1）=0.06，mi（Θ）=0.94（i=1，2，3，…，n）用D-S组合规则合成结果：m（θ1）=1-0.94n，m（θ2）=0.94n，当n值较大时，合成后m（θ1）就变得很大。如n→50时，m（θ1）=0.954 7，这显然是错误的。

2 单一证据——冲突表示方法存在的问题

2.1 冲突系数k的局限性

在经典证据理论中，冲突系数k是用来衡量冲突大小的，k值越大，说明证据间的冲突越大。但如果证据间交集不为空，单纯用k表示证据冲突会出现与直觉相悖的情况。

例3：设辨识框架为Θ={θ1，θ2，θ3，θ4}；系统两条证据分别为：m1（θ1）=m1（θ2）=m1（θ3）=m1（θ4）=0.25；m2（θ1）=m2（θ2）=m2（θ3）=m2（θ4）=0.25；则经典冲突系数k=0.75，其实这两个证据相同，直觉判断冲突为零。

例4：设辨识框架为Θ={θ1，θ2，θ3，θ4}；系统两条证据分别为m1（θ1∪θ4）=0.9；m1（θ2∪θ3∪θ4）=0.1；m2（θ1∪θ4）=0.1；m2（θ2∪θ3∪θ4）=0.9；可得，冲突系数为0，但实际上对于焦元θ1、θ2或者θ3而言，这两个证据的冲突是非常大的。

2.2 证据距离度量冲突的局限性

Jousselme［12］提出用证据距离描述冲突并计算证据间相似度作为证据权重。之后，各种基于J氏距离的改进方法相继提出，但这些方法均需计算两两证据距离，计算量较大。此外，J氏距离虽然表示了证据间相容焦元基本置信值分配的差异，但有时会出现与直觉相悖的情况。

例5：设辨识框架为Θ={θ1，θ2，θ3}；系统3条证据分别为m1（θ1）=0.5，m1（θ2）=m1（θ3）=0.25；m2（θ1）=m2（θ2）=0.25，m1（θ3）=0.5；m3（θ1）=m3（θ2）=0.1，m3（θ3）= 0.8。直观推断证据1与证据2的冲突应大于证据2与证据3的冲突，而计算得d12=0.25，d23=0.45。所以在用J氏距离度量冲突时也存在着“死角”。

针对单一冲突表示的局限性，LIU W［15］于2006年提出，用经典冲突系数k和博弈信度距离difBetP作为一个二元组来描述证据冲突，其后蒋雯［16］指出difBetP距离无法有效区分对系统未知和对系统各命题支持度相等这两种不同情况，加之difBetP距离不满足距离函数三公理，提出用经典冲突系数k和J氏距离来描述证据冲突并定义容忍极限ε作为判断冲突的参数，但对ε的设定并未给出一个准则与评价体系。刘准钆［17］用证据距离和矛盾因子的几何均值来表示冲突大小，但对于信任偏移悖论中k值总是为零的情况，得到的冲突大小为零，这并不符合实际，并且在计算J氏距离与k时，需求出两两证据距离以及两两证据冲突系数，当证据数量急剧增加时，会出现计算量指数级爆炸问题。

3 复合型冲突表示方法

实际应用中，各传感器对证据的获取是有先后顺序的，融合实质上是一个先前证据融合结果与新加入证据再次融合的过程。为此，本文采取动态融合处理的策略，即每次都用新加入的证据与前一步组合结果进行融合，得到新的合成结果，并提出一种利用复合型冲突度量的动态加权证据融合方法。首先利用给出的证据中心定义，在计算证据距离时，仅计算每条证据与证据中心的距离，在计算经典冲突系数k时，仅计算每条证据与证据中心的冲突系数，以减少两两求解的计算量，其次，提出利用当前中心距离与经典冲突系数k来共同表征冲突，并给出了复合型冲突大小及生成证据权重的表达式，最后用Dempster组合规则合成。

定义2Jousselme［12］距离：若m1和m2是在识别框架Θ上的两个BPA，则m1和m2的距离可以表示为

D为一个2N×2N阶矩阵，其中的元素为

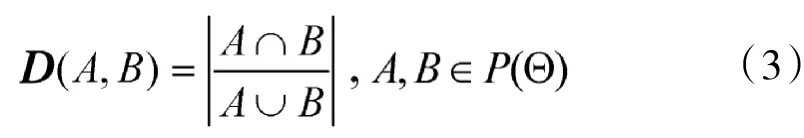
将式（2）代入式（3）可得

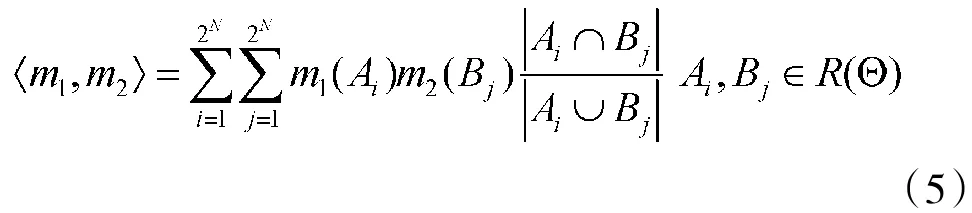
定义3证据中心：因为证据是序贯式加入的，证据中心在不断地更新，给出的当前证据中心为

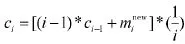
定义4当前中心距离：一个新证据加入组合结果序列后，若与证据中心距离越大，说明此证据成为干扰的可能性越大，其作用应该受到抑制。分别计算新加入证据与加入前后证据中心的距离，并求出几何均值作为当前中心距离，更能客观反应当前新入证据与已有证据的差异性。定义新入证据与当前证据中心ci的距离为；新入证据与加入之前的证据中心ci-1的距离，ci-1），当前中心距离为。

定义5复合冲突系数ξ：为当前中心距离d与冲突系数k的算术平均值，。

4 利用复合型冲突表示的动态加权证据修正

（2）第3步至第k步：

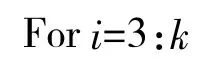
f、Dempster组合规则可得当前第i步的组合结果记为：

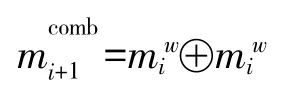
5 算例实验与讨论

为验证本文算法解决典型悖论问题的效果，分别与经典的修改证据源方法进行对比。其中D-S为经典合成方法，Murphy平均法［5］是最具代表性的证据修正方法，邓勇［8］及韩德强［7］方法利用的是单一冲突表示方法：在计算两两证据间J氏距离的基础上，确定各个证据权重并合成。

实验环境为Intel酷睿2.50 GHz，内存2 GB的PC机，VS2010软件平台。耗时取10次重复实验的平均值。

算例1：Zadeh悖论

设识别框架Θ={θ1，θ2，θ3}，BBA分别为：

m1（θ1）=0.99，m1（θ2）=0.01，m1（θ3）=0；

m2（θ1）=0，m2（θ2）=0.01，m2（θ3）=0.99；

mi（θ1）=0.99，mi（θ2）=0.01，mi（θ3）=0（i=1，2，3，…，n）；

表1为针对Zadeh悖论各种证据组合方法的结果。除DS方法外，其余方法均可有效解决Zadeh悖论。其中Murphy、邓勇方法收敛速度较快，韩德强方法与本文方法收敛速度较慢，但这并未影响对支持命题的决策。同其他方法一样，本文方法在第3个证据加入时，便可以得出正确结论。需要指出的是，算法的收敛速度并不是越快越好，过快的收敛速度对于违背直觉的结果来说更加速了错误决策的发生。算例2充分说明了这一点。

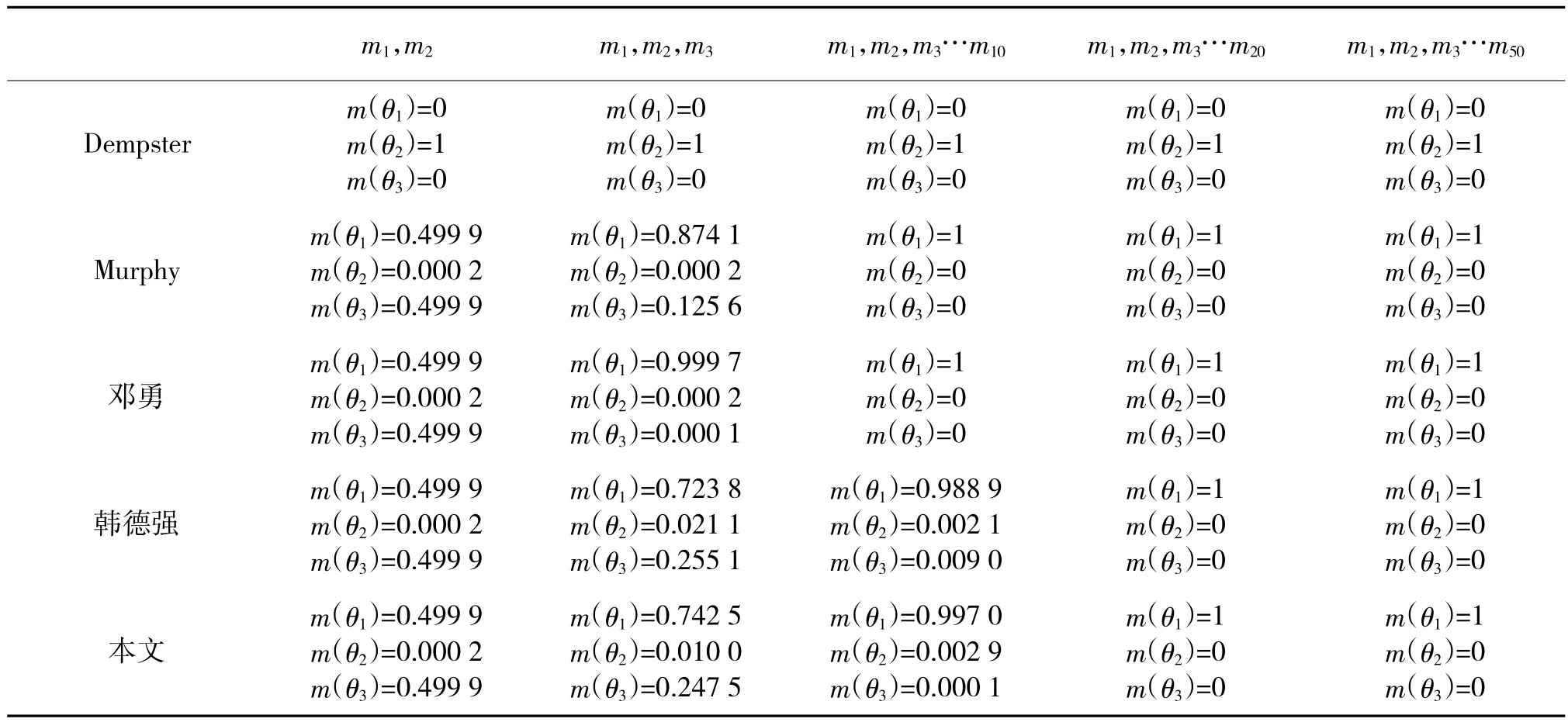
表1 各种证据组合方法的结果比较

算例2：信任偏移悖论

设识别框架Θ={θ1，θ2，…，θn}，BBA为m1（θ1）= 0.06，m1（Θ）=0.94，mi（θ1）=0.06，mi（Θ）=0.94，（i=2，3，…，n），本例着重验证在大规模证据合成时，算法能否以较短的计算时间更加有效地抑制悖论的发生，因此，令识别框架中的焦元数为50。

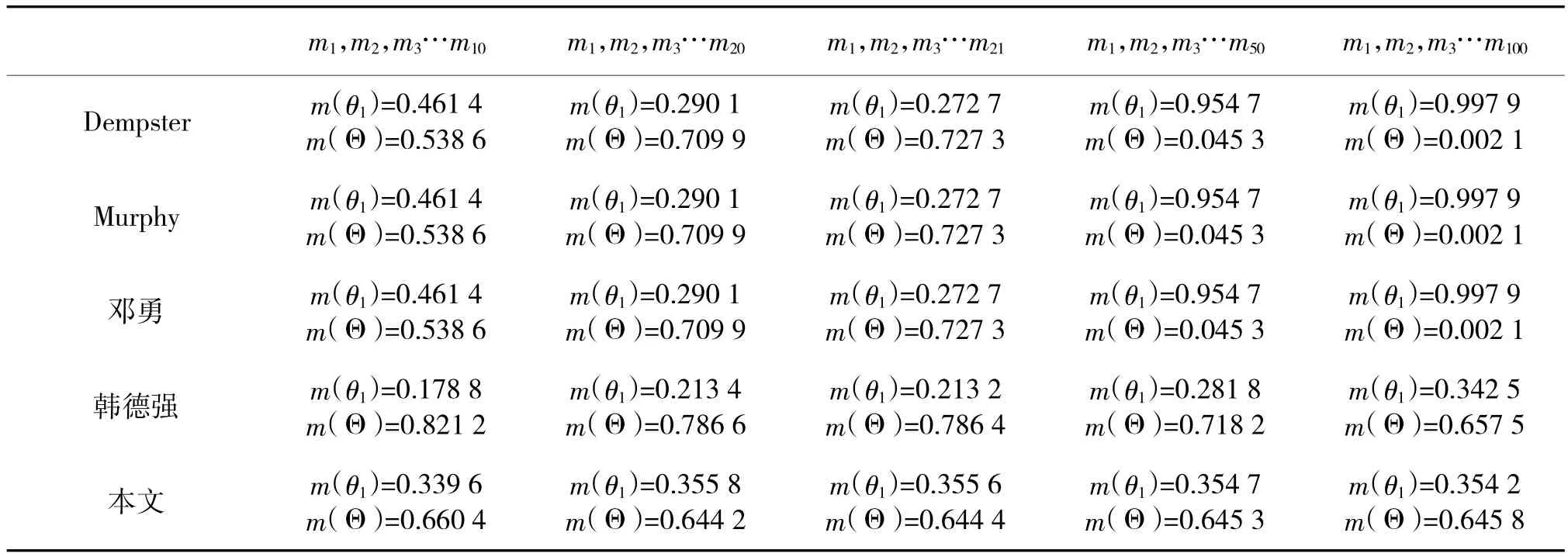
表2 证据组合结果比较

在算例2中，Dempster方法、Murphy方法、邓勇方法在新加入第12个证据时，就已经发生了信任偏移，此时m（θ1）=0.524 1，之后的合成结果向原本支持度很小的焦元θ1快速收敛，这更加剧了信任偏移的发生。韩德强方法中，随着证据数目的增多，对焦元θ1的基本概率指派也不断增加，虽然增速较前3种方法大大降低，但当证据数目急剧增加到一定程度时，信任偏移始终无法避免。本文算法中，当证据数目小于20时，和韩德强方法一样，对焦元θ1的基本概率指派也在缓慢增加，到达了极值之后，随着新证据的加入，对焦元θ1的基本概率指派开始缓慢减小，组合结果逐渐向符合人类直觉的方向收敛，虽然收敛速度比较平缓，但相比韩方法，彻底避免了信任偏移的发生。这是因为复合型冲突度量方法能够弥补单一冲突表示的“死角”问题，进而生成的证据权重更加全面地反应了各个证据的重要重度；另外，文中定义的证据中心随着相同证据的加入时时更新，并不断向基本概率指派中占优的焦元Θ逐步靠近，从而有效抑制了信任偏移。从融合速度上来说，本文算法由于增加了证据中心及当前中心距离的计算，相较于Dempster方法、Murphy方法耗时更多，如图1所示，但与邓勇、韩德强方法相比，并不需要求解两两证据距离。因此，在大规模证据融合时，能够避免信任偏移的发生并且耗时较短。本文算法更适用于证据规模较大时的稳妥保守型决策场合，并且证据数目越多，合成效果越好。

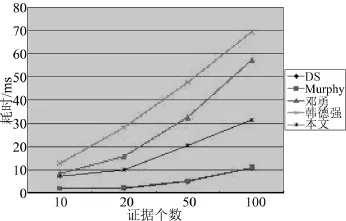
图1 各种方法组合证据序列2时的耗时趋势图

6 结束语

为解决利用经典DS规则进行大规模证据融合时的出现的悖论问题，从分析单一冲突表示方法的缺陷入手，提出一种利用复合冲突表示解决大规模证据合成时的DS快速加权融合算法。理论分析和数值实验结果表明，该方法在解决Zadeh悖论问题时，具有较好的收敛性；特别是在解决信任偏移悖论问题时，相较于其他算法，能够彻底避免信任偏移的发生。同时，在大规模证据融合时，算法显示了更快地计算速度。

［1］Dempster A P.Upper and Lower Probabilities Induced by a Multi-valued Mapping［J］.Annals of Mathematical Statistics，1967，38（2）：325-339.

［2］Shafer G.A Mathematical Theory of Evidence［M］.Princeton：Princeton University Press，1976.

［3］Destercke S，Burger T.Revisiting the Notion of Conflicting Belief Functions［C］//Proc of the 2nd Int Conf on Belief Functions.Compiègne，2012：153-160.

［4］Yang J P.A Novel Information Fusion Method Based on Dempster-Shafer Evidence Theory for Conflict Resolution［J］.Intelligent Data Analysis，2011，15（3）：399-411.

［5］Murphy C K.Combining Belief Functions When Evidence Conflicts［J］.Decision Support Systems，2000，29（1）：1-9.

［6］Haenni R.Are Alternatives to Dempster’s Rule of Combination Real Alternative Comments on“About the Belief Function Combination and the Conflict Management Problem”［J］. Information Fusion，2002，3（4）：237-239.

［7］韩德强，邓勇，韩崇昭，等.基于证据方差的加权证据组合［J］.电子学报，2011，39（3A）：153-157.

［8］邓勇，施文康，朱振福.一种有效处理冲突证据的组合方法［J］.红外与毫米波学报，2004，23（1）：27-32.

［9］吴俊，程咏梅，曲圣杰，等.基于三级信息融合结构的多平台多雷达目标识别算法［J］.西北工业大学学报2012，30（3）：367-372.

［10］Han D Q，Deng Y，Han C Z，et al.Weighted Evidence Combination Based on Distance of Evidence and Uncertainty Measure［J］.J of Infrared and MillimeterWaves，2011，30（5）：396-400.

［11］Atiye S J，Babak N A，Augustin T.Information-based Dissimilarity Assessment in Dempster-Shafer theory［J］. Knowledge-Based System，2013（54）：114-127.

［12］Jousselme A L，Grenier D，Bosse E.A New Distance Between two Bodies of Evidence［J］.Information Fusion，2001，2（2）：91-101.

［13］Zadeh L.On the Validity of Dempster’s Rule of Combination［R］.Memo M 79/24，Univ.of California，Berkeley，1979.

［14］张所地，王拉娣.Dempster-Shafer合成法则的悖论［J］.系统工程理论与实践，1997，17（5）：82-85.

［15］Liu W.Analyzing the Degree of Conflict Among Belief Functions［J］.Artificial Intelligence，2006，170（11）：909-924.

［16］蒋雯，张安，邓勇.改进的二元组冲突表示方式［J］.红外与激光工程，2009，38（5）：936-940.

［17］刘准钆，程咏梅，潘泉，等.基于证据距离和矛盾因子的加权证据合成法［J］.控制理论与应用，2009，26（12）：1439-1442.

A Method of Fast Weighted Evidence Combination Exhibited by Compound Conflict

BAI Dong-ying1，2，WANG Gang2，LI Song2，YAO Xiao-qiang2
（1.Second Artillery Engineering University，Xi’an 710025，China；
2.Air and Missile Defense College，Air Force Engineering University，Xi’an 710051，China）

Aiming at the paradox of D-S evidence theory and computation’s exponential growth in dealing with large–scale conflict evidence combination，a new weighted evidence combination method is proposed，which uses conflict coefficient and evidence distance in order to measure the conflict. Through the analysis of single conflict representation’s weaknesses，compound conflict coefficient has been put forward，meanwhile，the evidence centre and current centre distance are defined，evidence weight is determined with current centre distance and conflict coefficient.The experiment results show that the algorithm settles the paradox effectively，at the same time，computing speed has been greatly enhanced.

D-S evidence，conflict coefficient，evidence centre，centre distance

TP212.9

A

1002-0640（2015）12-0022-05

2014-12-18

2015-02-16

国家自然科学基金资助项目（61102109）

白东颖（1982-），女，陕西宝鸡人，博士研究生。研究方向：智能信息处理和机器学习。