纯方位目标运动分析可观测性研究*

杨婧，李银伢，戚国庆，盛安冬

（南京理工大学，南京210014）

纯方位目标运动分析可观测性研究*

杨婧，李银伢，戚国庆，盛安冬

（南京理工大学，南京210014）

纯方位目标运动分析（BOTMA）仅利用方位信息实现对目标状态参数的估计，是一种有效的无源被动定位跟踪方法。纯方位系统中的可观测性条件、目标跟踪与估计策略、观测器最优机动轨迹构成了BOTMA的核心研究内容。可观测性问题是BOTMA首先必须解决的关键问题，可观测性条件是后续目标定位与跟踪的前提和基础。介绍了纯方位系统中可观测性的基本概念，从几何方法、线性与非线性方法、数值分析方法等角度，对BOTMA的可观测性研究成果进行了系统的总结和评述，最后对这一领域的研究提出了新的展望。

可观测性，BOTMA，被动跟踪

0 引言

纯方位目标定位与跟踪是最经典的被动式无源定位跟踪技术，具有隐蔽性好、作用距离远、抗干扰能力强等优点，在无线电探测、被动声纳、红外等领域有着广泛的应用背景［1-4］。纯方位目标运动分析（Bearings-Only Target Motion Analysis，BOTMA）指的是，利用传感器被动地测量目标的方位信息，实时估计出目标的位置和运动（速度、航向）参数，达到对目标进行被动定位与跟踪的目的。BOTMA旨在掌握运动目标参数（状态）随时间的变化规律，建立和预测目标运动状态的历程和趋势，为后续武器系统的进一步动作，诸如攻击要素的获取奠定基础。BOTMA由于其固有的非线性和弱可观测性，使得该领域的研究具有极大的难度和挑战性。BOTMA的研究内容主要包括三个方面：目标可观测性条件，观测器最优机动轨迹以及目标定位跟踪算法［5］。其中，可观测性研究是后续研究的前提和基础。在纯方位系统中，BOTMA的可观测性问题本质上是非线性系统的可观测性问题。与线性系统不同，非线性系统具有局部可观测性和弱可观测性等特点，其研究过程涉及李代数等繁复的数学内容［6］，使得该类系统可观测性的分析研究更为困难。

图1 纯方位系统及其可观测性研究趋势

图1给出了SCI和EI两大数据库中涉及纯方位系统及其可观测性研究的检索结果。其中，“条件一”标识曲线代表纯方位系统研究的检索结果，检索关键词为“bearings-only”；“条件二”标识曲线代表纯方位系统可观测性研究的检索结果，检索关键词为“bearings-only&observability”。从图1可大致看出，纯方位系统及其可观测性问题的研究起源于上世纪六七十年代［7-8］，在经历了相对平缓的发展过程后，近十年来逐渐成为研究热点。而分析现有文献可知，可观测性问题的研究工作在八九十年代取得了较大进展，许多经典成果为后续的研究奠定了基础［9-11］。

1 可观测性概念

可观测性概念是卡尔曼在20世纪60年代首先提出的，表征系统状态能否由其输出完全反映的问题［12］。

在纯方位系统中，观测器测量的是目标相对于观测器的偏转角度，因此，在笛卡尔坐标系下，系统的量测方程是非线性的。以图2所示二维情形为例，设目标和观测器的坐标分别为和o），目标和观测器的状态向量xT（t）和xo（t）分别为

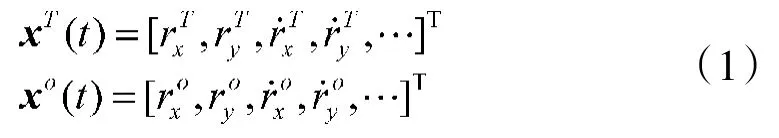
设β（t）为t时刻观测器测得的目标方位角，则系统的状态方程与量测方程分别为

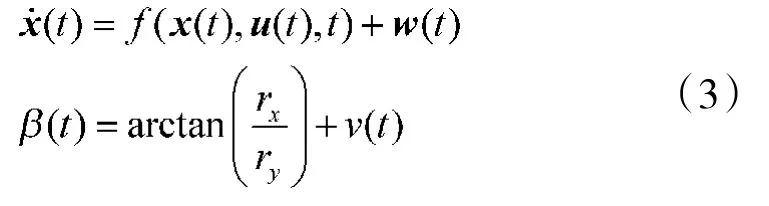
其中，u（t）为控制量，表示观测器相对于目标的机动；rx和ry分别为目标相对观测器在x轴、y轴方向上的位置坐标分量；w（t），v（t）分别为状态噪声和量测噪声。

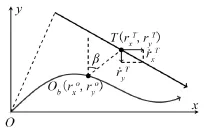
图2 目标与观测器运动态势

记t时刻目标状态的信息集合为

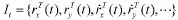
相应地，t=t0初始时刻的目标参数集合为

2 可观测性研究

可观测性分析是BOTMA中最核心也是最基础的研究内容。一方面，具有良好可观测性的纯方位系统，可以大幅度提高观测器对目标状态参数估计的可靠性和准确性。

2.1 几何分析方法

用几何方法进行目标定位通常可得到与实际运动参数相关联的结论，比较直观易懂。测向交叉定位法是一种发展较早，应用广泛的无源定位方法。文献［13］对二维和三维目标的可观测性进行了直观的分析。在二维情况下，观测器每次测量只得到方位角信息；在三维情形下，一次测量可得目标的方位角和高低角。其结论可归纳为，目标可观测要求观测器与目标有相对运动。文献［14］介绍了双站测向交叉定位法，基本原理与单站情形相同，同时给出了单站对匀速目标航向的计算方法。文献［15］提出线面相交定位法，比传统方法具有更高的定位精度。文献［16］用初等几何方法，得到了用方位信息计算匀速直线运动目标距离的公式。为保证可观测性，观测器采用折线运动方式。文献［17］也在观测器折线运动条件下分析了纯方位系统的可观测性，实现了对匀速目标的距离和速度的估计。

2.2 线性系统分析方法

在笛卡尔坐标系下，BOTMA中的测量方程是非线性的，给后续分析带来诸多不便。对测量方程进行伪线性化处理可以将测量方程转化为线性形式，然后运用线性系统理论分析可观测性。不考虑量测误差，对式（3）中量测方程进行代数变换可得

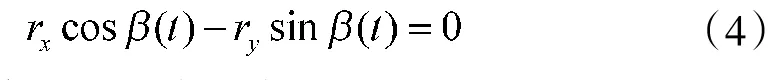
用矩阵向量形式可表示为

上式即为伪观测方程，C（t）称为伪观测矩阵，其维数由状态向量决定，y（t）是伪观测值。相应地，对式（3）中的状态方程作线性化处理，可得伪线性化后的纯方位系统动态方程为

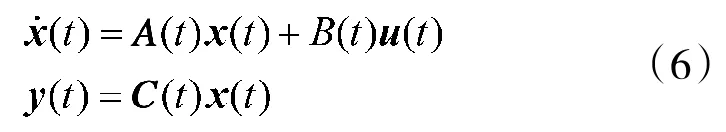
式中，x（t）∊Rn，y（t）∊Rm，A（t）∊Rn×n，B（t）∊Rn×p，C（t）∊Rm×n。因此，由式（3）描述的系统可观测性问题就转化为式（6）所示线性系统的可观测性问题。

下面介绍相关的分析方法。

判据1（Gram矩阵判据）［18］考虑式（6）描述的线性时变连续系统，系统在时刻t0完全能观测的充分必要条件是存在一个有限时刻t0∊Tt，t1＞t0，使如下定义的Gram矩阵：

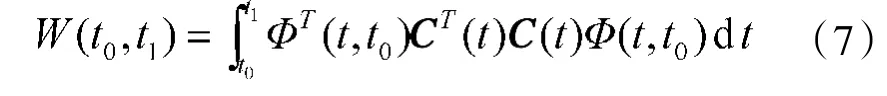
为非奇异，其中Φ（t，t0）为A（t）状态转移矩阵。

应当注意，上述判据中，Gram矩阵只包含C（t）和Φ（t），从控制理论的角度看，可观测性与输入无关［19］。但在BOTMA问题中，输入u（t）代表观测器相对于目标机动，u（t）的变化会影响测得的方位角信息β（t），而观测矩阵C（t）=［cosβ（t）-sinβ（t）0 0…］，所以输入u（t）会影响BOTMA可观测性能。

可观测性的Gram矩阵判据需要先计算状态转移矩阵，再求Gram矩阵，计算困难且计算量较大，故有以下简化的判据［19-20］。

判据2线性时变系统（6）在时刻t0完全能观测的充分条件是存在一个有限时刻t1∊Tt，t1＞t0，使

其中，M（t）=C（t）Φ（t，t0），Φ（t，t0）为A（t）的状态转移矩阵。

与判据2等价的判据3［19-20］如下：

判据3设线性时变系统（6）中，矩阵A（t），C（t）都为（n-1）阶连续可导的，则系统状态在时刻完全能观测的充分条件是存在一个有限时刻t1∊Tt，t1＞t0，使

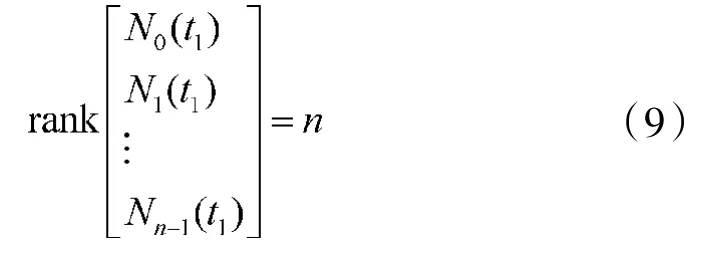
其中

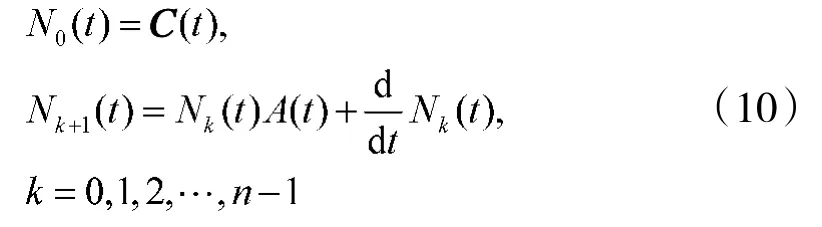
由判据1可推导如下等价的判据4和判据5［19-20］：

判据4系统（6）在时刻t0完全能观测的充要条件是，存在一个有限时刻t1∊Tt，t1＞t0，使矩阵C（t1）Φ（t1，t0）的N个列线性无关。

判据5系统（6）在时刻t0完全能观测的充要条件是，对任意的非零矢量ξ，存在t∊［t0，tf］，使得C（t）Φ（t，t0）ξ≠0。

Aidala［9］、Hammel［10］等利用上述线性系统的可观测性判据对BOTMA可观测性进行分析，其方法和结论被广泛引用。文献［9］对二维情况下的匀速直线运动目标，将量测方程伪线性化，运用判据2推导出了目标可观测条件：

其中，ao（t）是观测器加速度矢量，ao（t）和v（t0）分别是目标相对于观测器的初始位置和速度矢量，α（t）为任意标量时间函数。文献［10］将结论推广到了三维目标，得到了形式类似的可观测条件，不同的是推导过程中运用了判据3，简化了步骤。文献［11］将研究对象从匀速运动目标扩展到N阶动态运动目标，用代数方法得到了可观测的充分必要条件，推导过程极为简单，避免了求解微分方程，同时指出文献［9］和文献［10］的可观测判据只是必要非充分条件。而文献［21］根据判据4也得出了N阶动态运动目标不可观测的充要条件，其形式是观测器相对于目标的机动向量，即系统输入u关于目标初始状态的表达式，在实际中代表观测器的无效机动。笔者还进一步证明了文献［9］和文献［10］的结论是目标为一阶的特殊情况。同样基于线性系统方法，文献［22］运用判据5，经过简单的代数推导即可得文献［9-11］的结论，说明了以往线性系统方法在解决BOTMA可观测性问题时所呈现出的繁琐过程并不是线性系统方法本身的原因，而是与可观测性判据的选用有关，其结论使得线性系统方法得到了广泛应用［23-29］。文献［30］认为这种方法不局限于对N阶动态运动目标的分析，还可处理更广泛一类目标的情况，比如对于一阶延迟目标加速模型，当观测器的运动也满足一阶延迟模型时，要使得目标可观测，只须使观测器的机动时间常数不同于目标，观测器不必作比目标更高阶次的机动运动，这与N阶动态运动目标的可观测条件是截然不同的。该结论同样适用于随机环境下，目标加速度为Singer模型及其改进形式的情况。此外，文献［3，31］利用向量变换和线性方程组解的性质推导出N阶动态运动目标的不可观测条件，也简化了推导过程，为线性系统框架内的可观测性研究提供了新的思路。

基于线性系统分析方法的BOTMA可观测性分析研究，可以得到观测器的无效机动表达式，即可观测条件的解析形式，相对几何分析方法而言，研究方法在数学上更为严谨。然而，该类方法尽管在可观测性条件上给出了解析表达式，却一般是以目标和观测器的相对运动参数（或其导数）而不是以便于直接获取的方位量测来表示的。在实际工程应用中，常希望建立直接利用方位量测数据，无需求导和求解目标相对位置与运动参数的BOTMA可观测性判据，以简化操作，提高工程实用性。

2.3 非线性系统分析方法

纯方位系统本质上是非线性系统，利用非线性系统分析方法对BOTMA可观测问题可以进行更广泛、更深入的研究。与线性系统的Gram矩阵判据类似，Lee和Dunn等人提出如下可观测性判据［32］：

判据6对于如下非线性系统：

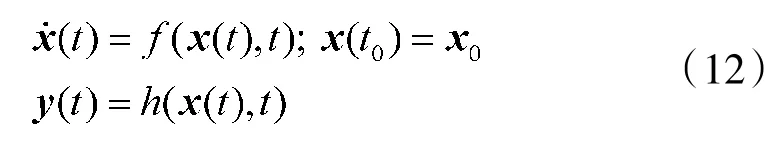
如果对于凸集S∊Rn上的所有x0，都有

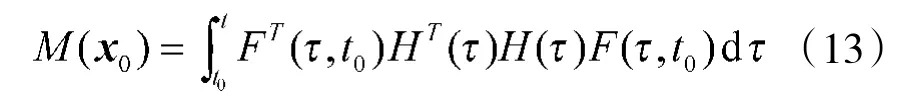
是正定的，则系统在S上是完全可观测的。其中

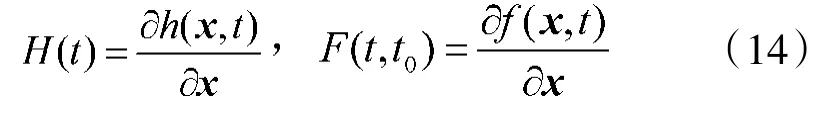
将上述判据与线性系统Gram矩阵判据比较可知，在非线性系统中用相应的Jacobin矩阵代替了线性系统的状态转移矩阵和测量矩阵。

将非线性系统弱可观测和局部可观测的概念相结合，还可得出与线性系统类似的局部弱可观测性的秩判据如下［2，33］：

判据7设非线性系统为

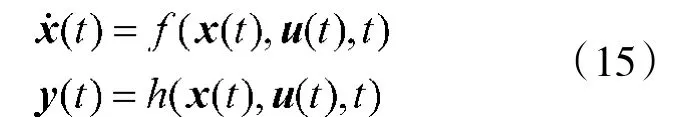
其中，x∊Xn⊂Rn，y∊Rm。可观测性矩阵定义为

对x0∊Xn，如果rank（Q）=n，则称系统在x0处是局部弱可观测的；如果对任意x∊Xn，都有rank（Q）= n，则称系统是局部弱可观测的。其中，N是如下定义的非线性算子：

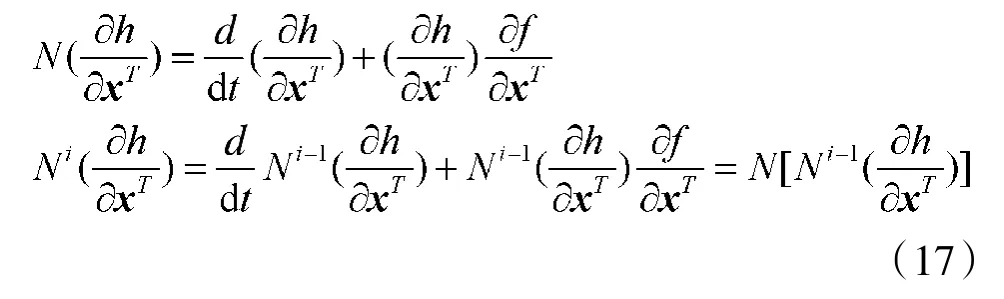
上述非线性系统分析方法在BOTMA的可观测性研究中得到广泛应用［34-37］。特别是文献［38］从实际应用出发，证明了非线性离散系统可观测性判据的“一致性”要求在系统初始状态和输入属于紧集时并非必须满足。只要系统状态两两可区分，且对于每个状态变量和输入，存在一定长度的观测序列使得可观测性判据的秩条件成立，那么整个系统就是可观测的。这种将可观测性判据“化整为零”的思路是符合实际需求的。

非线性系统方法在一定程度上可以看作是基于Gram矩阵的线性系统方法的推广，因此，适用于线性和非线性目标模型，使可观测性问题的研究扩展到了更广阔的领域。在数学原理上，用矩阵的正定或满秩条件作为可观测性判据。不足的是，当处理高阶目标时会产生较大的计算量。

2.4 数值分析方法

前面介绍的可观测性分析方法一般适用于判断系统全体状态变量在某一时刻是否可观测，是一种总体的定性分析。对于时不变系统，若系统是可观测的，并不能得知系统各状态的可观测程度；而对于时变系统，则需要分析从0时刻到t时刻的可观测性矩阵的秩或正定性，计算量很大。基于线性代数理论的数值方法可以对可观测性进行更为深入细致的定量分析。

文献［39］先计算系统可观测性矩阵Q，然后将正定对称阵QTQ单位化后的特征值λi定义为其所对应的状态向量或状态向量线性组合的可观测度。当0≤λi≤1，且λi越大，其特征向量所对应的状态向量或状态向量线性组合的可观测度越好；λi=0，则所对应的状态向量或状态向量组合不可观测。文献［40-41］对可观测性矩阵进行奇异值分解，并用奇异值大小判断可观测度。当可观测性矩阵是实矩阵时，有QH=QT，这与文献［39］的方法实质上是相同的。文献［42］根据线性代数理论定义了系统可观测矩阵的伪逆矩阵，将状态向量解的表达式分为固定部分和自由部分，自由部分决定系统的可观测性，给出了计算不可观测程度的公式。

文献［43］用系统可观测矩阵的条件数定义可观测度，条件数越大，则可观测度越差；若条件数是无穷大，则系统不可观测；条件数等于1时，可观测度最好。特别对于时变系统，文献［43］通过计算其局部可观测矩阵的条件数定量地分析系统在某些时刻的可观测性能，从而可对系统在任意时段内的可观测性进行定量分析。文献［44］基于条件数给出一种非线性系统可观测性度量方法，并指出系统可观测度依赖于状态模型和观测模型，与观测数据本身无关，可作为比较观测模型优劣的一个性能准则。

可观测矩阵的奇异值（或特征值）分析方法不仅可以定性判断整个系统是否可观测，还可定量分析系统各状态的可观测度；而基于条件数的方法适用于研究时变系统在某一时间段内的可观测性，这些都与实际工程中系统可观测性及后续研究的需求相符。

2.5 基于分段匀速直线运动模型的分析方法

在工程实际中，复杂的系统模型不利于问题的分析和求解，对模型进行简化操作是一种有效的解决方法。文献［45］认为，一些线性时变系统用分段定常系统（Piece-Wise Constant System，PWCS）模型近似时，可保留系统特性，引入了简化的可观测性矩阵分析PWCS系统的可观测性。文献［46］改进了文献［45］的方法，减少了计算量。以上述研究为依据，文献［47］用分段匀速直线运动模型描述目标和观测器的运动，分析了多种情形下纯方位系统的可观测性问题。其主要结论有：（1）如果目标做匀速直线运动，观测器运动轨迹由多段匀速直线运动构成，则目标是可观测的，当且仅当观测器每一段轨迹测得的目标方位变化率不全为零。（2）如果目标和观测器的运动轨迹都由多段匀速直线运动构成，那么目标是可观测的，当且仅当系统满足下列条件：①目标和观测器的所有机动时刻都不同且目标的机动时刻已知；②观测器轨迹至少包括2段匀速直线运动；③不存在方位变化率为零的分段。（3）如果目标和观测器的所有机动时刻都不同，目标的机动时刻未知且观测器轨迹没有方位变化率为零的分段，那么目标是可观测的。

文献［47］认为如果目标运动轨迹由多段匀速直线运动构成，观测器做匀速直线运动，那么目标是不可观测的。文献［48-50］的研究则表明如果观测器的速度矢量vo和目标轨迹中相邻的两段速度矢量vs，1，vs，2满足voT（vs，1-vs，2）≠0，那么此时目标可观测。文献［51-52］进一步研究了目标轨迹包含匀速转弯（Constant Turn，CT）运动，而观测器仍做匀速直线运动的情形，结合文献［48］有如下结论：①只要观测器不是静止的，则任何做CT运动的目标都是可观测的；②如果观测器静止，则存在测量方位角与真正目标同位相似的假目标；③BOTMA可以区分CT运动目标和CV目标，即②中假目标不会是CV目标；④如果目标运动轨迹由多段CV和CT运动组成，那么在至少有一段为CT运动的条件下，目标的整个轨迹是可观测的。

2.6 有噪条件下的可观测性分析方法

BOTMA的可观测性研究一般只考虑无噪声影响的确定性系统，文献［4］则将实际观测量视为受随机噪声干扰的随机变量，认为纯方位系统实质上是状态方程连续、量测方程离散的非线性随机系统，其观测性能更适宜用“好”和“差”来描述。考虑到估计量的Fisher信息矩阵（Fisher Information Matrix，FIM）是衡量系统估计量好坏的性能指标，因此，可作为判定纯方位系统可观测性的依据。当FIM不可逆时，系统是不可观测的；若FIM可逆，但具有大条件数，此时系统虽是可观测的，但观测性“较差”，反之若FIM可逆且不存在大条件数，此时系统是可观测的，且具有“好”的观测性。文献［53-54］还引入高斯条件下状态不确定超椭球体积，作为系统可观测度大小的度量。文献［55-56］对FIM的可逆性与非线性系统在无噪条件下的可观测性之间的关系进行了讨论，结果表明：如果在高斯独立噪声条件下，非线性系统的FIM在x0处可逆，那么相应的无噪系统在x0处是局部可观测的。应当注意该结论的逆命题不成立，即系统在某点处可观测并不能保证FIM在该点的可逆性。而对于线性系统，局部可观测性与全局可观测性是等价的。

FIM可以看作对系统整体可观测性的定量分析，利用数值方法则可对每个状态变量分别进行定量的可观测性分析，2.4节已对此详细总结，这里不再赘述。需要说明的是，文献［43，57］将系统可观测矩阵的条件数定义为可观测度，看似与文献［4，53］的可观测度定义不同，实际上二者原理相通［58］。FIM与可观测矩阵相比，前者包含了测量噪声的协方差，适合于分析有噪条件下的可观测性能，而后者适用于理想的无噪条件。

2.7 可观测性分析其他方法

近年来，对纯方位系统的可观测性问题，出现了一些新的研究思路，进一步拓展了BOTMA可观测性分析方法，丰富了BOTMA可观测性理论。文献［59］讨论一般目标的可观测性问题。这里“一般”的含义是指目标的运动假设突破了以往匀速直线运动等形式的限制，扩展为更一般各种复杂运动。指出在二维纯方位系统中，系统可观测的必要条件是观测器作比目标更为复杂的运动，并且独立方位数目等于待定参数数目。这一结论不仅有助于对纯方位系统本质的认识，对后续跟踪算法和观测器机动轨迹研究等都具有重要意义。连续和离散系统是纯方位系统的两种不同的表现形式，对于线性连续定常系统离散化后是否依然可观测，文献［18］给出了判断依据。但对线性时变系统和非线性系统而言，对应的可观测判据类比或转换比较困难，不利于实际应用。文献［60］证明了离散纯方位系统仅依赖方位测量的可观测判据，文献［61］则在连续系统下推导了该判据，表达形式与离散系统判据类似，但作者研究仅限于一阶目标，结论有待进一步推广。

对于海上运动目标，传统分析方法［62-63］一般忽略了声音在海水中的传播时间，认为声速为无限值。文献［64］对此提出了质疑，考虑到声音的传播需要一定时间，所以方位的测量必定与声速有关。由于海水中的声速受诸多因素影响，笔者将其设定为一个假想的平均速度。当目标做匀速直线运动且平均声速为有限常数时，证明了目标在观测器不机动时也是可观测的，且在相同的观测器机动条件下，目标可观测性要优于认为声速为无限值的情形。文章的研究结果表明，声速有限的假设包含了目标的状态信息，对于可观测性分析有重要价值。

基于图论的分析方法［65-66］常用于电力系统的状态可观测性分析，具有计算量小，速度快等优点。对于多站纯方位系统目标运动分析，其系统拓扑结构的复杂性远小于电力系统。文献［67-68］研究机器人仅依靠方位量测的协同定位问题，定义了相对位置测量图（Relative Position Measurement Graph，RPMG），结合非线性系统可观测判据建立了RPMG性质与可观测性的关系，从而得出可观测条件。该类方法在处理基于传感网络的BOTMA可观测性分析上，提供了新的研究思路和技术途径。

3 结束语

BOTMA的可观测性问题本质上属于非线性系统解的存在唯一性问题，但早期的研究者多采用线性系统的分析方法，对量测方程进行伪线性化处理。非线性系统理论的发展使可观测性问题的研究有了新的理论依据，研究对象也不再局限于N阶动态运动目标。尽管后来又有其他研究方法的出现，但线性和非线性系统方法仍然得到了最广泛的应用。20世纪八九十年代是可观测性研究发展的重要时期，出现了大量经典的研究成果，为后续的研究奠定了基础。而后来的学者们主要从两方面拓展丰富了前人的研究：一是寻找更为有效的方法，简化分析过程，用最简单的方法推导出已有的结论并将其融会贯通［69］；二是考虑实际应用需求，对可观测性的判据进行改进或是调整观测条件［70-73］。

综上所述，BOTMA可观测性的研究重点表现在以下两个方面：一是建立可观测性判据，判断所给系统是否可观测或研究其可观测程度；二是利用可观测性判据，研究可观测条件，并由此提出对观测器的数目、运动方式等方面的要求，以期改善系统可观测性能。前者力求判据的简单易用，后者则追求可观测条件的直观易懂。

从现阶段可观测性研究情况来看，可从以下几方面对BOTMA可观测性问题进行更深入的研究：

（1）连续系统和离散系统的可观测性研究方法不同，所得到的判据形式也不同，研究它们之间是否有类比或相互转换的可能，以使可观测理论更为完善，为实际应用提供便利。

（2）一些可观测条件是目标和观测器相对运动状态的表达式，而目标与观测器的相对运动通常是未知的，需要更为直观、实用的判据形式。诸如，能否建立直接基于方位量测数据，无须求导和求解观测器与目标的相对运动参数的可观测性判据?

（3）在有噪条件下，基于FIM的可观测性判定方法仅适用于低阶目标，对于高阶目标会产生很大的计算量，而对于更一般性的运动目标，相应的可观测性分析理论和方法仍有待深入研究。

（4）纯方位系统的可观测性和观测器与目标的相对运动形式密切相关。由于目标运动的未知性和不合作性，观测器本身的合理有效机动是保证纯方位系统可观测的首要条件。从工程应用角度出发，考虑观测器最大机动速度、机动次数、传感器探测盲区、战术意图、武器效能等实际因素制约下的观测器机动模式，将后续目标跟踪估计算法与观测器工程化机动轨迹研究紧密结合起来，从定性分析过渡至定量分析，寻求更具实用性和可操作性的可观测性分析方法，将是未来该领域研究的重要课题。

（5）可观测性研究的进展总是与研究分析方法的革新密切相关，因此，进行理论创新，寻求更为有效的研究途径将是未来该领域研究的重要方面。

［1］刘忠，周丰，石章松，等.纯方位目标运动分析［M］.北京：国防工业出版社，2009.

［2］潘泉，戴冠中.被动式跟踪可观测性分析的非线性系统方法［J］.信息与控制，1997，26（3）：168-173.

［3］Xu Z，Sheng A，Guo Z.The Analysis of the Unobservable Criteria on the Single Platform Bearings-only Target Tracking System［C］//IEEE International Conference on Networking，Sensing and Control，2008.

［4］权宏伟，彭冬亮，薛安克.纯方位角目标运动分析的可观测性研究［J］.火力与指挥控制，2009，34（10）：43-46.

［5］李洪瑞.水下目标运动分析关键技术研究［D］.南京：南京理工大学，2009.

［6］丁玉琴.几类非线性系统观测器设计研究［D］.济南：山东大学，2007.

［7］Kolb R C，Hollister F H．Bearing-only Target Motion Estimation［C］//Proceedings of 1st Asilomar Conference on Circuits and Systems，1967：935-946．

［8］Murphy D J．Noise Bearings-only Target Motion Analysis［D］.Ph.D.Dissertation of Northwestern University，1970.

［9］Nardone S C，Aidala V J.Observability Criteria for Bearingsonly Target Motion Analysis［J］.IEEE Transactions on Aerospace and Electronic Systems，1981，17（2）：162-166.

［10］Hammel S E，Aidala V J.Observability Requirements for Three Dimensional Tracking Via Angle Measurements［J］. IEEE Transactions on Aerospace and Electronic Systems，1985，21（2）：200-206.

［11］Fogel E，Gavish M.Nth-order Dynamics Target Observability from Angle Measurements［J］.IEEE Transactions on Aerospace and Electronic Systems，1988，24（3）：305-308.

［12］Kalman R E.Contributions to the Theory of Optimal Control［J］.Bol.Soc.Mat.Mexicana，1960，5（2）：102-119.

［13］吕文亭，黄亮，王澍初，等.无人机单站无源定位中的可观测性分析［J］.舰船电子工程，2013，32（11）：44-45.

［14］孙仲康，郭福成，冯道旺，等.单站无源定位跟踪技术［M］.北京：国防工业出版社，2008.

［15］杨柏胜.多站被动传感器定位技术研究［D］.西安：西安电子科技大学，2006.

［16］Gad A S，Mojica F，Farooq M.Geometric Approach to Target Tracking Motion Analysis in Bearing-only Tracking［C］//International Society for Optics and Photonics，2002. AeroSense 2002：1-12.

［17］Rao S K.Correspondence-Comments on Discrete-time Observability and Estimability Analysis for Bearings-only Target Motion Analysis［J］.IEEE Transactions on AerospaceandElectronicSystems，1998，34（4）：1361-1367.

［18］李先允.现代控制理论基础［M］.北京：机械工业出版社，2007.

［19］Chen C T，王纪文.线性系统理论与设计［M］.北京：科学出版社，1988.

［20］邓新蒲.单站无源定位可观测性评述［J］.中国工程科学，2007，9（11）：54-62.

［21］Payne A N.Observability Conditions for Angles-only Tracking［C］//Twenty-Second Asilomar Conference on Signals，Systems and Computers.IEEE，1988.

［22］Becker K.Simple Linear Theory Approach to TMA Observability［J］.IEEE transactions on Aerospace and Electronic Systems，1993，29（2）：575-578.

［23］许兆鹏，韩树平.多基阵纯方位非机动目标跟踪可观测性研究［J］.传感器与微系统，2012，30（12）：57-59.

［24］Zhu W，Xu Z，Li B，et al.Research on the Observability of Bearings only Target Tracking Based on Multiple Sonar Sensors［C］//2012 Second International Conference on Instrumentation，Measurement，Computer，Communication and Control（IMCCC）.IEEE，2012：631-634.

［25］Zhu W，Xu Z，Li B，et al.Research on the Observability of Acceleration Based on Multiple Sonar Sensors［C］//2012 International Symposium on Information Science and Engineering（ISISE）.IEEE，2012：3-6.

［26］黄耀光，李建新，高博.基于空频域信息的单站无源定位可观测分析［J］.指挥控制与仿真，2012，34（5）：46-49.

［27］冯道旺，李宗华，周一宇，等.一种单站无源定位方法及其可观测性分析［J］.国防科技大学学报，2004，26（1）：68-71.

［28］熊茂涛，张勇，吴钦章.基于纯方位量测的三维运动目标可观测性研究［J］.现代防御技术，2009，37（4）：30-34.

［29］Jauffret C，Pillon D.Observability in Passive Target Motion Analysis［J］.IEEE Transactions on Aerospace and Electronic Systems，1996，32（4）：1290-1300.

［30］Song T L.Observability of Target Tracking with Bearings-only Measurements［J］.IEEE Transactions on AerospaceandElectronicSystems，1996，32（4）：1468-1472.

［31］许志刚.TMA中不完全量测估计与观测平台机动模式研究［D］.南京：南京理工大学，2009.

［32］Lee T S，Dunn K P，Chang C B.On Observability and Unbiased Estimation of Nonlinear Systems［M］.System Modeling and Optimization.Springer Berlin Heidelberg，1982：258-266.

［33］Hermann R，Krener A J.Nonlinear Controllability and Observability［J］.IEEE Transactions on Automatic Control，1977，22（5）：728-740.

［34］乔梁.外辐射源角度测量定位算法可观测性分析［J］.青岛科技大学学报：自然科学版，2011，32（4）：426-428.

［35］曲毅，刘忠，彭鹏菲.基于垂直线阵无源定位的可观测性研究［J］.舰船科学技术，2009，31（6）：91-94.

［36］乔梁.信源定位的可观测性及跟踪技术研究［D］.哈尔滨：哈尔滨工程大学，2010.

［37］Yi Y Z，Zhong K S.Observability Analysis of Single Passive Observer［C］//Proceedings of the IEEE 1995 National Aerospace andElectronics Conference.IEEE，1995.

［38］Hanba S.On the“Uniform”Observability of Discrete-time Nonlinear Systems［J］.IEEE Transactions on Automatic Control，2009，54（8）：1925-1928.

［39］冯绍军，袁信.观测度及其在卡尔曼滤波器设计中的应用［J］.中国惯性技术学报，1999，7（2）：18-21.

［40］Yang B，Yao Y，He F.Passive Ranging Based on Observability Analysisand Receding Horizon Filter［J］.Tsinghua Science&Technology，2009，14（s2）：32-37.

［41］Chang X，Cui P，Cui H.Observability Analysis of Autonomous Navigation system of Interplanetary Spacecraft［C］//Chinese Control and Decision Conference，2009. IEEE，2009：766-770.

［42］Dong J L，Mo B.The Method of System Observability Analysis Using Pseudo-inverse of System Observability Matrix［C］//2013 32nd Chinese Control Conference（CCC）. IEEE，2013：55-59.

［43］刘准，陈哲.条件数在系统可观测性分析中的应用研究［J］.系统仿真学报，2004，16（7）：1552-1555.

［44］常晓华，崔平远，王晓明，等.基于条件数的能观性度量方法及在自主导航系统中的应用［J］.宇航学报，2010，31（5）：1331-1337.

［45］Goshen-meskin D，Bar-itzhack I.Observability Analysis of Piece-wise Constant Systems.I.Theory［J］.IEEE Transactions on Aerospace and Electronic Systems，1992，28（4）：1056-1067.

［46］Kong X，Guo M，Dong J.An improved PWCS Approach on Observabilityanalysis of Linear Time-varying System［C］//Proceedings of the 21st Annual International Conference on Chinese Control and Decision Conference.IEEE Press，2009：816-820.

［47］Le Cadre J P，Jauffret C.Discrete-time Observability and Estimability Analysis for Bearings-only Target Motion Analysis［J］.IEEE Transactions on Aerospace and Electronic Systems，1997，33（1）：178-201.

［48］Jauffret C，Pillon D，Pignol A C.Bearings-only Maneuvering Target Motion Analysis from a Nonmaneuvering Platform［J］.IEEE Transactions on Aerospace and Electronic Systems，2010，46（4）：1934-1949.

［49］Jauffret C，Pillon D，Pignol A C.Bearings-only TMA without Observer Maneuver［C］//2008 11th International Conference on Information Fusion.IEEE，2008：1-8.

［50］Jauffret C，Pillon D，Pignol A C.Leg-by-leg Bearings-only TMA without Observer Maneuver［C］//Proceedings of the International Conference on Information Fusion.Seattle，USA：2009.

［51］Clavard J，Pillon D，Pignol A C，et al.Bearings-only Target Motion Analysis of a Source in a Circular Constant Speed Motion from A Non-maneuvering Platform［C］//Proceedings of the 14th International Conference on Information Fusion（FUSION）.2011：1-8.

［52］Clavard J，Pillon D，Pignol A C，et al.Target Motion Analysis of a Source in a Constant Turn from a Nonmaneuvering Observer［J］.IEEE Transactions on Aerospace and Electronic Systems，2013，49（3）：1760-1780.

［53］吴京，王博，李骏，等.空间目标天基光学跟踪可观测性分析［J］.湖南大学学报：自然科学版，2009，36（11）：32-37.

［54］Fang X，Yan W，Wang Y，et al.Observability Analysis of Underwater Localization Based on Fisher Information Matrix［C］//2013 32nd Chinese Control Conference（CCC）. IEEE，2013：4866-4869.

［55］Jauffret C.Observability and Fisher Information Matrix in NonlinearRegression［J］.IEEETransactionson Aerospace and Electronic Systems，2007，43（2）：756-759.

［56］Pignol A C，Jauffret C，Pillon D.Properties of Range-only Target Motion Analysis［C］//2013 16th International Conference on Information Fusion（FUSION）.IEEE，2013：1693-1698.

［57］夏佩伦.纯方位目标跟踪系统的可观测程度［J］.火力与指挥控制，1992，17（2）：23-29.

［58］孙仲康，周一宇，何黎星，等.单多基地有源无源定位技术［M］.北京：国防工业出版社，1996.

［59］夏佩伦.一般仅方位目标跟踪系统可观测的必要条件［J］.电光与控制，2011，18（6）：1-4.

［60］李洪瑞，盛安冬.离散纯方位系统的可观测性判据［J］.控制理论与应用，2009，26（5）：570-572.

［61］李洪瑞，盛安冬.连续纯方位系统的可观测性分析［J］.兵工学报，2009，30（11）：1446-1450.

［62］董志荣.纯方位系统定位与跟踪的本载体最优轨线方程及其最优轨线［J］.指挥控制与仿真，2007，29（1）：7-15.

［63］石章松，刘忠.单站纯方位目标跟踪系统可观测性分析［J］火力与指挥控制，2007，32（2）：26-29.

［64］李长文，赵建昕.声速有限条件下的纯方位方法［J］.指挥控制与仿真，2012，34（5）：94-98.

［65］Parlangeli G N G.Controllability and Observability of Grid Graphs Via Reduction and Symmetries［J］.arXiv Preprint arXiv，2012（129）：1203-1204.

［66］Doostmohammadian M，Khan U A.Topology Design in Net-worked Estimation：A Generic Approach［C］//American Control Conference（ACC），2013.

［67］Sharma R，Beard R W，Taylor C N，et al.Graph-based Observability Analysis of Bearing-only Cooperative Localization［J］.IEEE Transactions on Robotics，2012，28（2）：522-529.

［68］Sharma R，Quebe S，Beard R W，et al.Bearing-only Cooperative Localization［J］.Journal of Intelligent&Robotic Systems，2013，72（3-4）：429-440.

［69］Li H，Chen L，Sheng A.Two-step Modeling and Observability for Bearings-only Tracking［C］//International Conference on Mechatronics and Automation，2009.

［70］刘忠，邓聚龙.多传感器系统纯方位定位与可观测性分析［J］.火力与指挥控制，2004，29（5）：79-83.

［71］刘忠.单静止站纯方位系统的可观测性与目标参数估计算法［J］.海军工程大学学报，2004，13（5）：20-23.

［72］刘忠，邓聚龙.等速运动观测站纯方位系统的可观测性［J］.火力与指挥控制，2004，29（6）：51-54.

［73］Ferdowsi M H.Observability Conditions for Target States with Bearing-only Measurements in Three-dimensional Case［C］//Computer Aided Control System Design，2006 IEEE International Conference on Control Applications，2006 IEEE International Symposium on Intelligent Control. IEEE，2006.

Overview of Observability of Bearings-only Target Motion Analysis

YANG Jing，LI Yin-ya，QI Guo-qing，SHENG An-dong
（Nanjing University of Science and Technology，Nanjing210014，China）

Bearings-Only Target Motion Analysis（BOTMA）is an efficient method for passive localization and tracking due to the superiority of which uses only bearing measurements to estimate parameters of target motion.The researches of bearings-only systems concentrate on three aspects：observability conditions，target tracking and estimation strategies and optimal observer maneuver trajectories.The observability problem is the key issue that is to be handled firstly because the corresponding observability conditions are the basis and precondition of follow-up researches of target localization and tracking.First，the basic concept of observability in bearings-only system is introduced. Then from the research methodology perspective，the existing BOTMA observability research results，including geometric methods，linear and nonlinear system based methods and numerical methods，etc.，are summarized and reviewed.Finally，several new opinions on future researches in this area are presented.

observability，BOTMA，passive tracking

TP271

A

1002-0640（2015）12-0001-08

2014-11-05

2015-01-15

国家自然科学基金（61273076，61104186）；江苏省自然科学基金资助项目（BK2012801）

杨婧（1990-），女，山西运城人，硕士研究生。研究方向：水下纯方位系统的可观测性。