一种新的二次雷达信号盲分离算法*
樊斌斌,张玉,唐波
(电子工程学院,合肥230037)
一种新的二次雷达信号盲分离算法*
樊斌斌,张玉,唐波
(电子工程学院,合肥230037)
针对应答脉冲信号的混扰现象影响二次雷达询问机解码的问题,提出了一种基于和差单脉冲天线以及二次雷达信号代数性质的二次雷达信号盲分离新算法。该算法通过分析二次雷达信号的ZCM(零/恒模)特性,采用了一种用于二次雷达信号分离的代价函数,进而由代价函数最小值对应的单脉冲比求解得到混合矩阵和分离矩阵,最终实现二次雷达信号的盲分离。仿真结果表明,当信噪比不低于20 dB时,该算法无需任何先验条件可有效分离出二次雷达信号。
二次雷达信号,和差单脉冲天线,ZCM特性,代价函数
0 引言
二次雷达(Secondary Surveillance Radar,SSR)是利用地面询问机对机载应答机的应答信号进行解码,从而探测定位目标的系统[1]。在复杂电磁环境中,传统二次雷达A/C模式极易受到干扰,造成询问机的解码错误。尽管单脉冲技术和模式S的引入,在一定程度上减轻了混扰问题。但随着空中交通流量的高速增长,还面临着混扰环境中的应答信号分选和解码问题[2]。因此,准确地分离混叠信号,对提高二次雷达信号分选性能具有重要意义。
目前国外针对二次雷达信号盲分离研究的公开文献较少,国内对二次雷达信号盲分离研究方法有文献[3]中的基于负熵最大的FastICA(固定点)算法、文献[4]中的基于盲源分离的等变化自适应分离(EASI)算法等。基于负熵最大的FastICA算法采用定点迭代的优化算法,具有较好的收敛性,但对信号模型和分离性能未进行深入研究。基于盲源分离的等变化自适应分离算法虽然进行了性能分析,但采用峭度作为目标函数寻求独立分量时,容易受到干扰,影响算法的稳定。
针对应答信号可能不完全满足非高斯假设而造成Fast ICA算法对二次雷达信号分离性能不佳的不足,本文研究了一种基于和差单脉冲天线以及二次雷达代数性质的二次雷达信号盲分离算法。利用二次雷达的ZCM(零/恒模)特性提出了代价函数,再对代价函数进行分析得到最小值对应的单脉冲比,进而求解出混合矩阵和权值矩阵,最终完成信号的分离。本文提出的分离算法不需要任何先验条件,仿真结果验证了该算法的有效性。
1 二次雷达应答信号格式
1所示。每个码位有两种状态,即有脉冲(高电平,为“1”)或者无脉冲(低电平,为“0”)。框架脉冲F1和F2恒为“1”状态,它们之间的间隔为20.3 μs。X位是备用位,恒为“0”。两个框架脉冲之间的其余12个码位C1、A1、C2、A2、C4、A4、B1、D1、B2、D2、B4、D4为真正的信息码位,包括目标的应答信息。SPI是特殊位置识别码,一般不用。
应答信号的脉冲宽度为0.45 μs,相邻脉冲的间隔为1.45 μs,框架脉冲F2与SPI脉冲的间隔为4.35 μs。当SPI脉冲被激活时,该脉冲持续时间可达到15 s~30 s。其应答信号数学表达可以写作:
传统二次雷达实际上常用A、C两种模式。然而,它们的应答格式相同,由两个框架脉冲F1和F2、12个数据脉冲、一个备用位脉冲X以及一个特殊位置编码脉冲SPI组成,共16个信息码位,如图
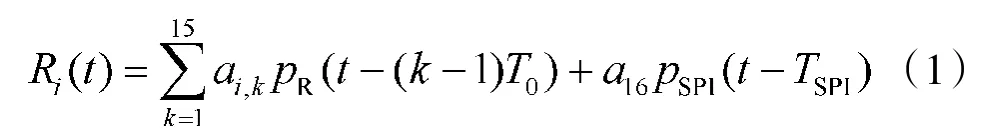
式中,T0=1.45 μs,pR(t)表示宽度为0.45 μs的矩形脉冲,pSPI(t)表示SPI脉冲。ai,1=ai,15=1,ai,8=0,TSPI=24.65 μs。
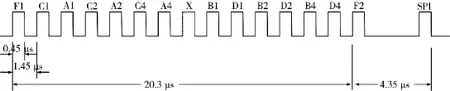
图1 传统模式应答格式
二次雷达S模式信号的频率与传统模式的相同,即询问频率为1 030 MHz,应答信号频率为1 090 MHz,具有特定的信号格式。应答信号格式(如图2所示[7])包括4个脉冲宽度为0.5 μs的前导脉冲以及一个应答数据块组成(56 μs或者112 μs),根据应答内容,应答数据块包含56或者112比特的数据,每个比特的数据采用曼彻斯特编码,即前0.5 μs为高电平、后0.5 μs为低电平时表示数据1,反之则表示数据0。

图2 S模式应答格式
2 基于和差单脉冲天线的盲分离算法
2.1 二次雷达信号的代数性质
二次雷达系统询问信号标称中心频率fc为1 030 MHz,应答信号标称中心频率fc为1 090 MHz。但受限于晶振实际频率的影响,接收机本振频率fe不会与标称中心频率完全相同,存在一定偏移频率f(f=fe-fc)。国际民航组织(ICAO-International Civil Aviation Organization)中规定可以允许的偏移频率为±3 MHz。由于受到偏移频率f的影响,二次雷达信号将不再是二进制信号,而是等于零或者分布在单位圆上。如果后续接收到的信号是非零的,那么这些信号满足以下相关因素:φn=exp(2πjfnTs)。因此,二次雷达信号满足ZCM特性。其静态性质表示为信号取值非零的位置包络恒定(恒模),即信号归一化后,对于任一采样点,sk(l)=0或|sk(l)|=1。其中,sk(l)表示第k个信号源第l个采样点的信号。数学描述如下:


2.2 算法概述及步骤
假设S模式地面二次雷达使用和差波束单脉冲天线,背景如图3所示。目标A和目标B均处于询问天线主波束范围内,因此,当询问机发出询问时,目标A和目标B都会收到来自主瓣的询问信号。根据测距原理,从询问机发射询问后到目标应答被触发、发出应答信号再到询问机收到应答信号所需时间为电磁波经过两倍目标距离加上应答的响应时间。对于目标A和目标B,如果它们的响应时间是相同的,询问机收到目标B的应答信号时间会滞后于目标A。当这个滞后时间太小,则会导致目标A的应答信号与目标B的应答信号重叠在一起。建立观测和、差信号的模型如下:
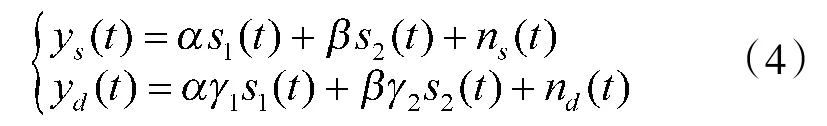
式中,α、β分别为两个源信号对应的幅度系数,γ1、γ2分别为目标A与目标B差波束输出与和波束输出的比值,即单脉冲比。s1(t)、s2(t)分别为两个相互独立的源信号。ns(t)、nd(t)为t时刻的噪声矢量,服从零均值高斯分布。
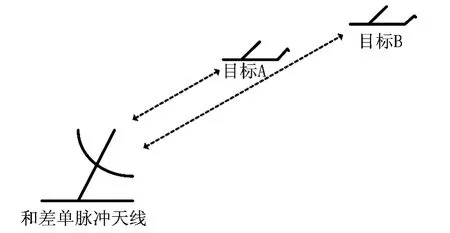
图3 接收信号模型图
为了便于数字处理,对式(4)进行模数转换,假设采样后信号长度为L,得到观测信号矩阵模型如下:
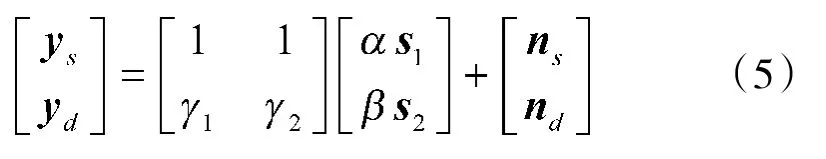
把和、差信号样本排列成2×L维的观测矩阵Y,则Y有如下形式:

由于源信号的幅度系数并不会对盲分离结果产生影响,且在信噪比较高的条件下,噪声可以忽略不计,因此,在理论上可以不用考虑幅度系数和噪声的影响。为了能够从混叠的应答信号中恢复出源信号S,首先要估计出混合矩阵A。利用盲源分离思想,可以在式(6)的两边同时乘以一个分离矩阵W,使得WA=I,从而得到源信号。由于AA-1=I,显然W=A-1,表示如下:
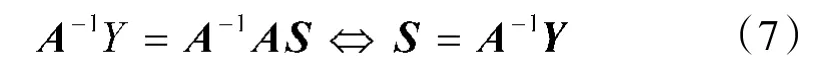


以上证明说明只要能准确地估计出目标A和B的单脉冲比γ1、γ2,就能从混叠的应答信号中分离出两个源信号。二次雷达信号满足ZCM特性,那么式(8)得到的L个输出信号都满足式(2)。取其和为代价函数,表示如下:

二次雷达信号的ZCM特性使得代价函数f在理想情况下等于零。但由于受到各种噪声的影响,代价函数不可能等于零,只能趋近于零。本文通过对代价函数分析,即分析二次雷达信号的代数特征,取代价函数两个最小值为对应的单脉冲比,从而得到混合矩阵A和权值矩阵w,最终计算得到源信号。算法步骤如下:
(1)利用输出信号与源信号的关系,建立矩阵模型,得到实际观测矩阵Y;
(2)定义权值矩阵w=[-γ1],得到输出信号x(k);
(3)利用二次雷达信号的ZCM特性,推导出代价函数f;
(4)分析代价函数,得到代价函数的最小值对应的单脉冲比;
(5)由单脉冲比求解得到的混合矩阵A和权值矩阵w,最终得到源信号。
2.4 算法性能指标
为了评价基于和差单脉冲天线以及二次雷达信号代数性质的二次雷达信号盲分离算法分离性能,采用分离指数E作为评价标准[11]。

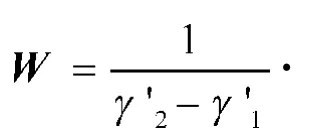
3 仿真结果及分析
假设有两个目标A和B收到询问信号,并同时发出应答信号,但由于滞后时间太短的原因,使得两个应答信号部分重叠在一起。针对同类信号混叠的情况,分别对同时为二次雷达S模式或A/C模式的应答信号进行盲分离,并设定参数幅度系数α=β=1,目标A和目标B的单脉冲比γ1=-0.2、γ2=0.1,信号S1实际频率为1 090.1 MHz,信号S2实际频率为1 089.9 MHz。询问机收到ModeS信号后使用20 MHz的采样频率对信号进行数字采样;收到ModeA/C信号后使用50 MHz的采样频率对信号进行数字采样。图4为分别来自不同信源相互独立的两个ModeS信号,信噪比为20 dB。图5为分别来自不同信源相互独立的两个ModeA/C信号,信噪比也为20 dB。
图6是在信噪比为20 dB条件下,采用本文算法对混叠信号进行分离过程中得到的代价函数图。从图6中可以读取出代价函数的两个最小值对应的单脉冲比,从而得到混合矩阵A和权值矩阵w,分离出源信号。

图4 ModeS信号图形
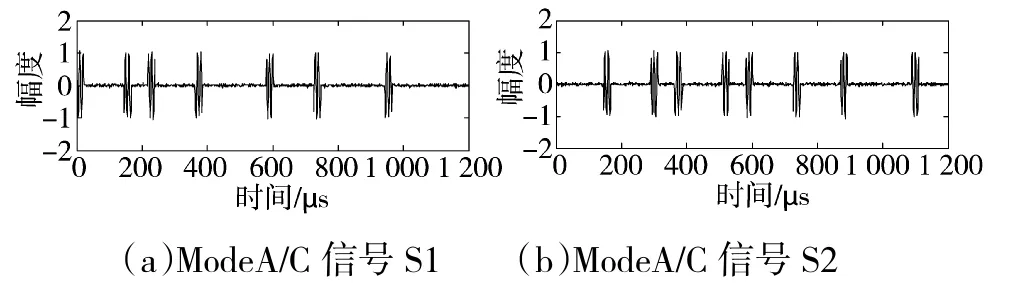
图5 ModeA/C信号图形
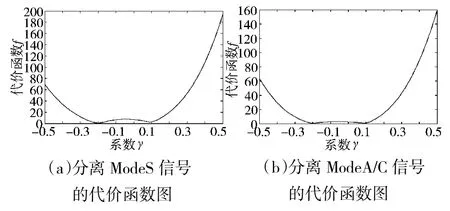
图6 代价函数图
图7 是当应答信号的信噪比从15 dB变化到45 dB时,利用本文算法和FastICA算法盲分离ModeA/C混叠信号,并进行了100次独立的蒙特卡罗实验后得到的平均分离指数曲线。图中明显可以看出FastICA算法在信噪比较高的条件下分离指数并不随之单调下降,而本文算法性能指数随信噪比的增加单调下降,性能优于FastICA算法。

图7 不同算法在不同信噪比下的分离指数
4 结束语
本文提出了一种新的二次雷达信号盲分离算法,首先建立观测信号矩阵模型,通过对二次雷达信号ZCM特性的分析,推导出代价函数方程,取代价函数极小值对应的单脉冲比,从而得到混合矩阵和分离矩阵,最终有效地分离出源信号。该算法在噪声条件下,不需要任何先验条件,克服了FastICA算法对二次雷达信号分离性能不佳的不足,对提高二次雷达信号分选性能具有重要意义。
[1]张尉.二次雷达原理[M].北京:国防工业出版社,2009.
[2]唐波,程水英,张浩.基于多通道阵列处理的二次雷达混扰信号分选[J].电讯技术,2014,54(5):534-540.
[3]顾军,胡显丹.基于FastICA算法的敌我识别信号分选方法研究[J].舰船电子对抗,2009,32(5):41-44.
[4]孙凌宇,罗静,屈金佑.混叠敌我识别信号分离算法研究[J].无线电工程,2011,41(1):18-21.
[5]孙守宇.盲信号处理基础及应用[M].北京:国防工业出版社,2007.
[6]由科军.盲信号分离算法研究[D].西安:西安电子科技大学,2009.
[7]兰鹏,曾一江,王凌.S模式地面二次监测雷达及其关键技术分析[J].电讯技术,2012,52(6):840-845.
[8]Petrochilos N.Algebraic Algorithms to Separate Overlapping Secondary Surveillance Radar Replies[J].IEEE,2007,55(7):3746-3759.
[9]马建仓,牛奕龙,陈海洋.盲信号处理[M].北京:国防工业出版社,2006.
[10]Jeroen T.Separation of Zero/Constant Modulus Signals[J]. IEEE,1997:3445-3448.
[11]Novey M,Adali T.On Extending the Complex FastICA Algorithm to Noncircular Sources[J].IEEE Transactions on Signal Processing,2008,56(5):2148-2154.
A New Blind Source Separation Algorithm of Secondary Surveillance Radar Signals
FAN Bin-bin,ZHANG Yu,TANG Bo
(Electronic Engineering Institute,Hefei 230037,China)
A blind source separation algorithm of SSR signals based on sum-difference monopulse antenna and algebraic property is proposed,which can overcome the problem of decoding errors of Secondary Surveillance Radar(SSR)due to the presence of garble.Firstly,the algorithm proposes a cost function for separating SSR signals by means of analyzing the Zero/Constant Modulus(ZCM)property of SSR signals.Then the algorithm finds the mixture matrix and weight matrix by using the monopulse ratio associated with the minimum value of cost function.Finally the algorithm separates the SSR signals with the weight matrix.The numerical simulation results show that the algorithm can separate the SSR signals effectively without any prior conditions when SNR is higher than 20 dB.
SSR signals,sum-difference monopulse antenna,ZCM property,the cost function
TN958.96
A
1002-0640(2015)12-0027-04
2014-11-19
2015-01-12
国家自然科学基金(61201379);安徽省自然科学基金资助项目(1208085QF103)
樊斌斌(1990-),男,浙江义乌人,硕士研究生。研究方向:信号与信息处理。

