基于流固耦合的螺旋桨水动力性能数值仿真

黄 胜 白雪夫 孙祥杰 陈广杰

（哈尔滨工程大学 船舶工程学院 哈尔滨150001）

引 言

复合材料螺旋桨作为一种新型的推进器，在船舶节能减排方面的作用日益为人们所重视［1］。利用复合材料螺旋桨的可设计性，通过合理安排桨叶的纤维方向和铺层顺序，可以使螺旋桨桨叶在水动力载荷作用下产生有利于水动力性能的变形。由于复合材料螺旋桨的特性，造成传统的模型水池试验成本高、周期长，传统的螺旋桨理论设计与计算建立在势流理论基础之上，未能全面考虑粘性的影响且不考虑旋度，因而无法准确预测桨叶边界层、螺旋桨尾流场的结构及桨叶梢涡的形成等真实情况下的流动特性。基于RANS方程的粘性流场计算螺旋桨的流场特性的方法日趋完善，黄胜等［2］分析螺旋桨在不同工作状态下的水动力性能。关于螺旋桨流固耦合计算方法的研究，LIN H J等［3］采用升力面法和九节点退化壳单元耦合算法，实现了求解复合材料螺旋桨的水动力性能的算法。Young Y L［4-5］研究面元法和软件ABAQUS耦合的螺旋桨流固耦合计算方法，但这些方法均是基于势流理论的螺旋桨水动力计算。

本文主要根据螺旋桨理论，结合计算流体力学方法和结构有限元方法［6］，基于ANSYS Workbench并调用CFD求解器Fluent和有限元Mechanical APDL，分别用于螺旋桨水动力模型和有限元模型两者的数值模拟计算，同时将两个求解器通过System coupling模块进行数值传递，完成螺旋桨流固耦合数值方法的构建。

1 数学模型

1.1 流体控制方程

考虑螺旋桨在粘性湍流中旋转，其连续性方程可表示为：

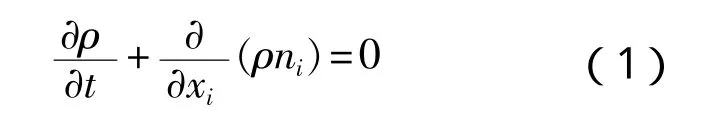
动量方程可表示为：

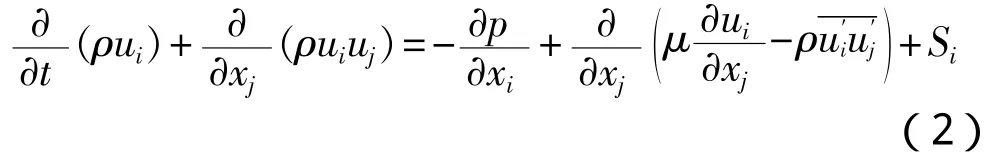
式中：p是静态压力，Pa；μ是湍流粘度；ρ是液体密度为Reynolds应力，Pa。

1.2 湍流模型的选取

不同的湍流模型有不同的适用性。在运用湍流模型进行计算时，首先要综合考虑不同湍流模型的模拟能力以及计算所需系统资源，在比较分析之后选择合适的湍流模型进行计算。常用的湍流模型有标准k-ε模型、可实现的k-ε模型、标准k-w模型和SSTk-w模型。本文通过比较分析几种常用湍流模型，通过求解时间和求解精度方面的对比以及流固耦合本身对计算机性能的要求等方面进行综合考虑。螺旋桨水动力性能计算模型选择SSTk-w湍流模型，该模型是利用混合函数将k-ε和k-w方程相结合而构建的湍流模型，在近壁区采用k-w方程，其他区域则采用k-ε方程以获得湍流粘性作用，考虑了k-w方程近壁区模拟时的有效性及远场区无法准确模拟的不足［7］，最终选择SSTk-w模型求解螺旋桨的流固耦合特性［8］。

1.3 数值离散方式

计算过程中对压力速度耦合方程采用SIMPLEC算法进行离散；动量方程、湍流动能、湍流耗散系数采用二阶迎风格式进行离散；压力离散格式采用PRESTO。

2 计算模型

2.1 桨的基本参数

本文流固耦合方法的构建与验证均以DTMB P4381模型桨为研究对象，其水动力模型主要采用多重参考模型（MRF模型），保持螺旋桨转速n=600 r/min，选择不同的进速系数进行水动力计算。设置与传统的CFD计算时稍有不同。表1为螺旋桨主要参数。

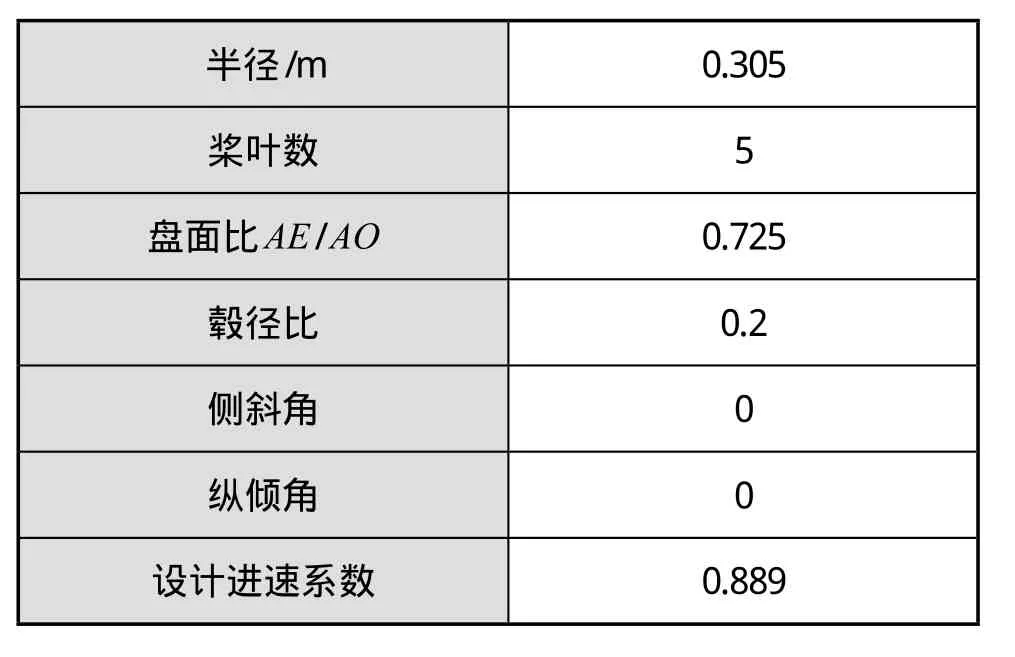
表1 螺旋桨主要参数

2.2 几何模型的建立与网格划分

圆柱体流场域使用与结构部分模型统一的坐标，圆柱体轴线与螺旋桨轴线一致。同时将整个流域分为大域与小域两部分，有利于网格划分与计算的设置。其中，大域圆柱体直径为3D，进口边界距离螺旋桨2D，出口边界距离螺旋桨5D；小域圆柱体直径为1.1D。将入口边界设置为速度入口，出口边界设置为自由出流，圆柱面、桨叶面和桨毂面都设置为无滑移固壁条件。采用混合网格方法：大域采用全结构化网格，以减少网格数目，加快计算速度；由于动网格设置的需要，小域采用自适应网格，并在叶片处对网格进行加密，以提高计算精度。划分完的网格如图1所示。

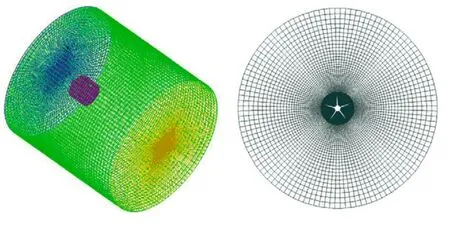
图1 流场网格划分

本文使用的是双向流固耦合的方法进行计算，故壁面会产生位移。通过System coupling模块将有限元求解器计算所得结构位移从FSI-solid传递到FSI-fluid，在Fluent中完成边界移动。

为实现因边界位移所产生的网格动态变化，需要运用动网格技术。本文将Fluent提供的弹簧光顺与网格重构两种动网格方法相结合，成功完成了网格动态变化的过程，保证了动网格的质量和计算精度。如图2-图3所示。

结构部分网格划分主要以四面体网格为主，在桨叶片处加密，以提高计算精度。划分完成的网格如图4所示，总网格数为120万。

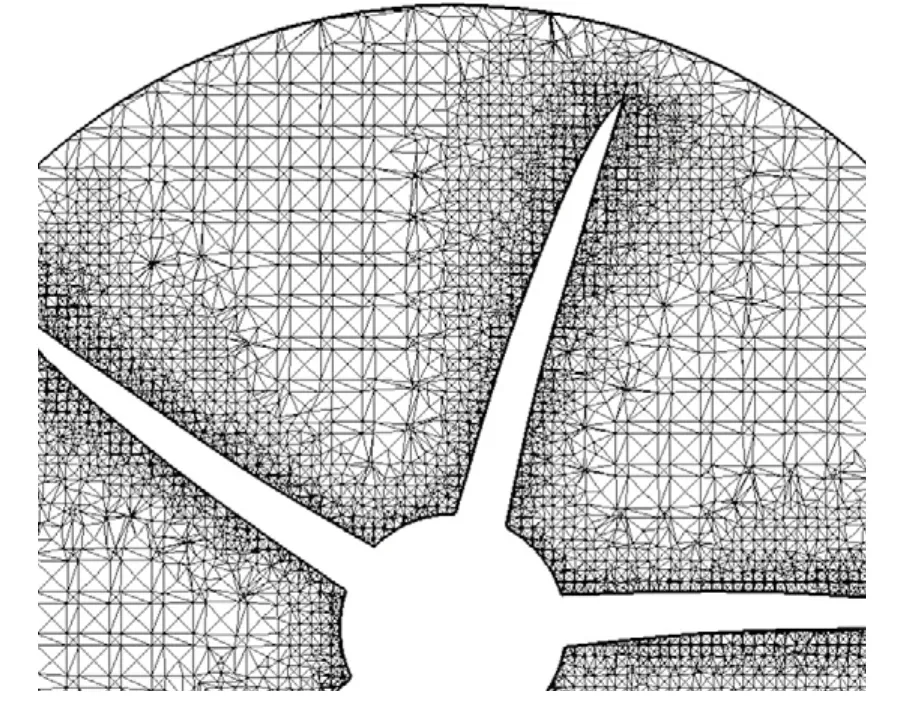
图2 原边界及网格

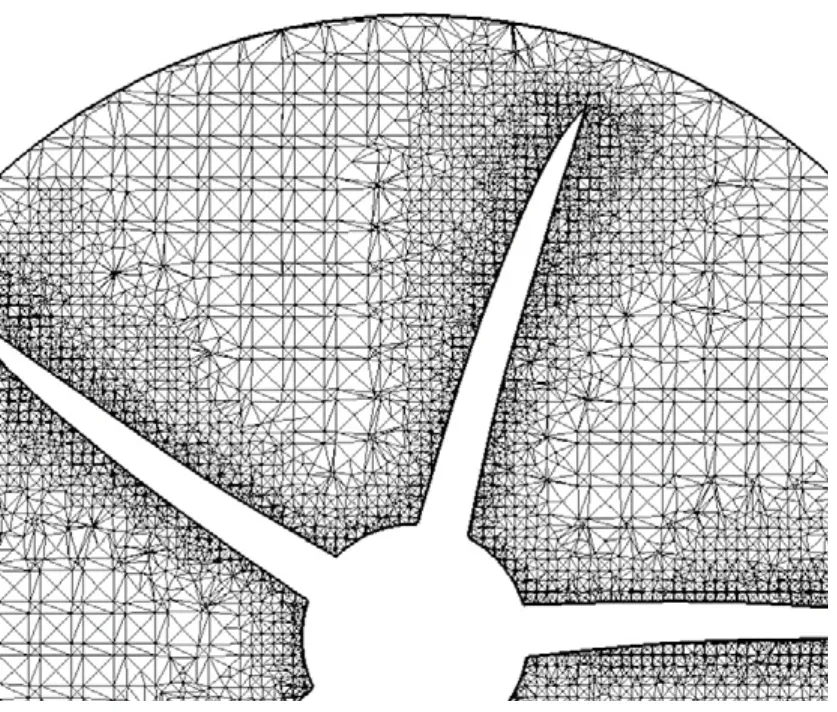
图3 变化后的边界及网格

图4 结构网格划分

2.3 螺旋桨结构有限元模型

本文不考虑螺旋桨材料的各向异性，选择典型的金属材料，其主要参数如表2所示。

表2 螺旋桨金属材料主要参数

2.4 约束与载荷

由于螺旋桨的桨毂和桨叶为一体化模型，故而在设置结构部分约束时，只需在桨毂处设置固定约束（Fixed Support）。

在进行螺旋桨的流固耦合分析时，以桨叶片处所受载荷为主。设置流固耦合面（Fluid Solid Interface），使用System coupling模块，将叶片所受载荷通过FSI-fluid传递到FSI-solid，完成叶片动态载荷的加载。

3 计算验证

运用已经建立的螺旋桨的流固耦合瞬态方法，对金属材料螺旋桨进行均匀来流情况下的水动力性能计算，并与文献中的实验值和传统的CFD方法计算结果进行比较，结果如图5-图7所示。

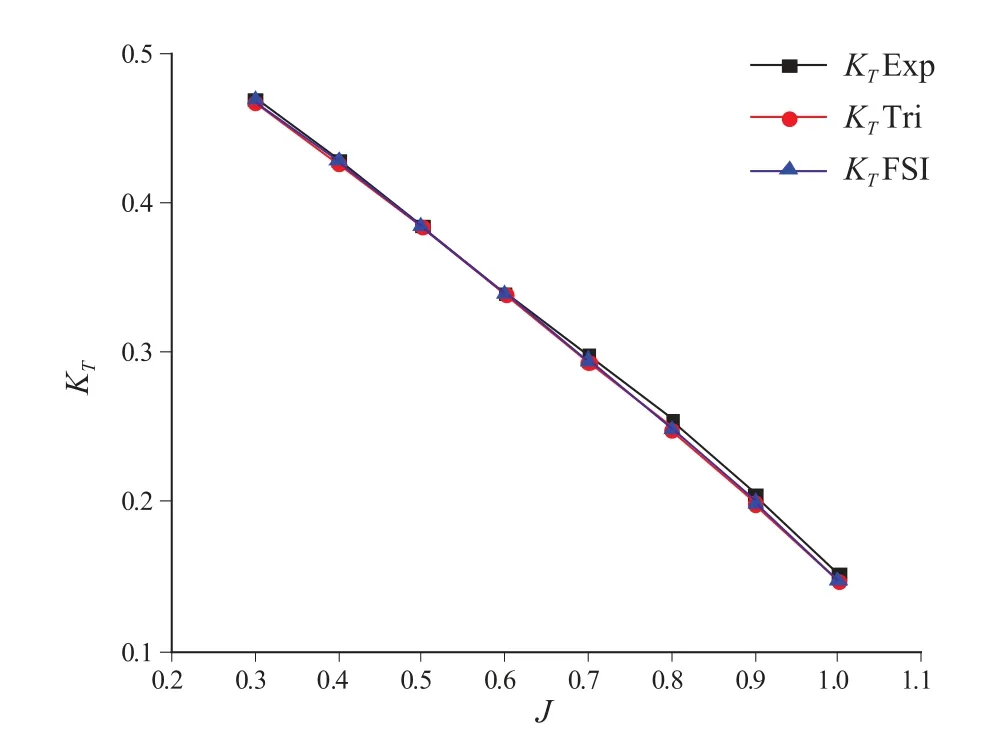
图5 螺旋桨推力系数

图6 螺旋桨转矩系数

由上面3组图可以看出，传统的CFD方法及本文构建的FSI稳态方法计算所得结果与实验值较为吻合。在均匀来流情况下的水动力性能曲线趋势一致，且传统CFD方法与FSI方法计算所得结果差异非常小。这是由于本章是以金属材料螺旋桨进行方法验证，流固耦合作用对螺旋桨桨叶的变形及敞水性能的影响极其微小，故无法直接通过敞水性能曲线准确分析FSI方法与CFD方法的差异。

将各个进速系数J下的CFD方法与FSI方法计算所得的KT、KQ及η0同实验值的误差进行比较分析，见下页表3。

由表3可以看出，CFD方法及FSI方法计算所得的KT、KQ及η0与实验值的误差均在±5%以内，各项数据误差整体趋势随着进速系数J的增加而增大。FSI方法计算误差较CFD方法误差略小，且在低进速情况下，FSI方法计算误差小的优势相对更加明显。随着进速的增加，两种方法的误差趋于一致。这是由于在低进速情况下，螺旋桨处于重载状态，水动力载荷作用于螺旋桨叶面所产生的变形相对于高进速轻载状态下所产生的变形更大，而FSI方法能够更好的捕捉桨叶的变形对金属材料螺旋桨水动力性能所带来的微小变化，模拟更加接近实际情况。

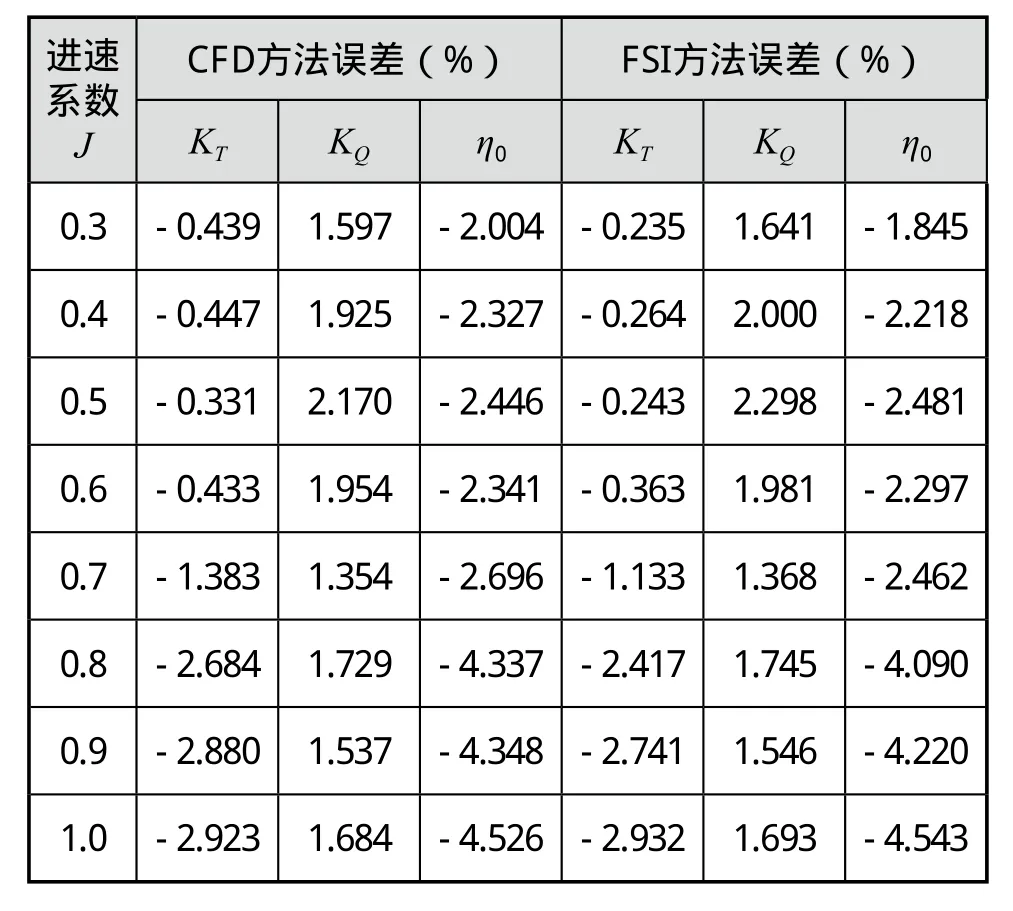
表3 传统CFD方法与FSI方法误差分析

图8显示的是不同进速系数下螺旋桨在轴向、径向及周向的变形，选取的进速系数J分别为0.3、0.7和1.0。由图8可知，在不同进速系数下，螺旋桨叶片均产生与来流方向相反的变形，变形沿着叶根向叶梢不断增大，类似悬臂梁变形，可认为螺旋桨产生了纵倾分布；同时在相同进速系数下，任意半径处叶元体变形量沿导边向随边逐渐变小，可认为螺旋桨各半径处的螺距角变小。

图9为不同进速系数下的螺旋桨径向变形分布。由图9可知，在不同进速系数下，螺旋桨叶片在径向产生变形，径向变形在导边靠近叶梢处为最大值，在叶面上朝向随边逐渐减小，而边缘处达到最小值。

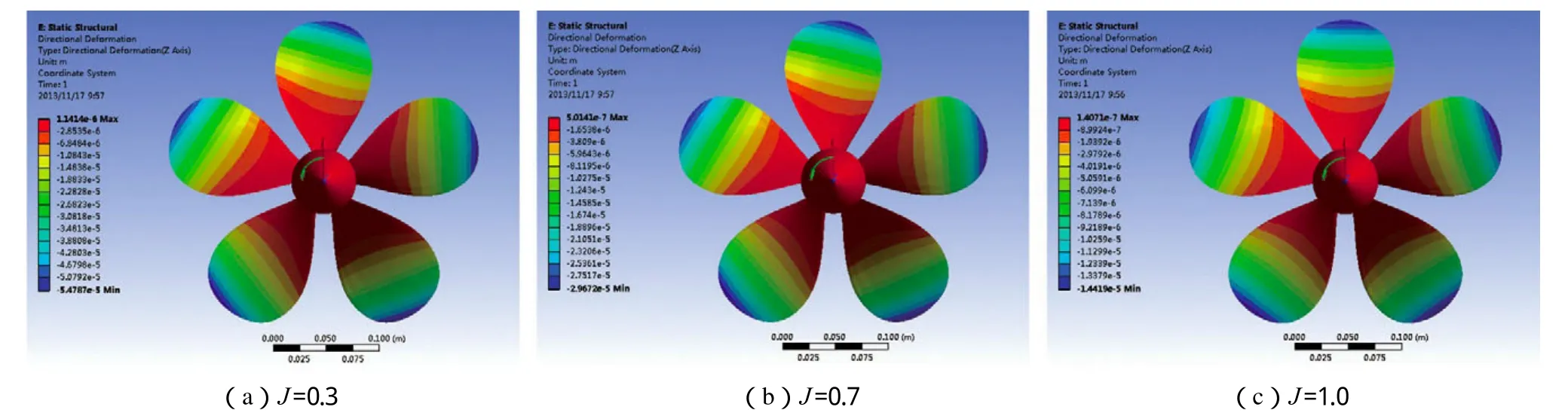
图8 不同进速系数（J） 下的 螺旋桨桨叶轴向变形分布

图9 不同进速系数（J） 下的螺旋桨桨叶径向变形分布

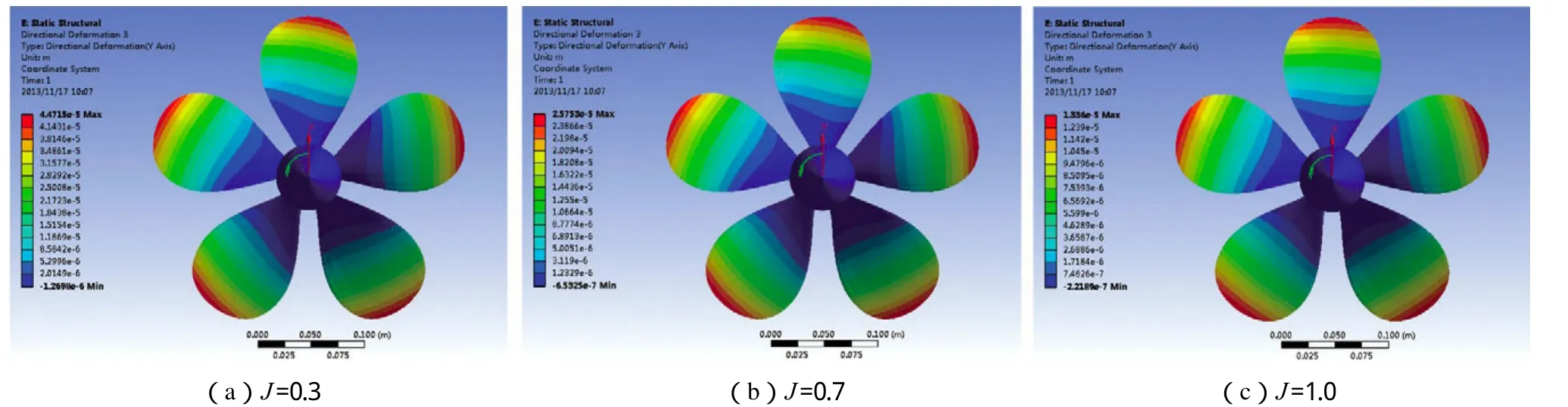
图10 不同进速系数（J） 下的螺旋桨桨叶周向变形分布

图10为不同进速系数下的螺旋桨桨叶周向变形分布。由图10可知，在不同进速系数下，螺旋桨叶片均产生与螺旋桨转向相反的周向变形，变形沿着叶根向叶梢不断增大，可认为螺旋桨产生了侧斜。

总体上看，相同转速下，螺旋桨的轴向变形、径向变形及周向变形在低进速下均大于高进速，轴向变形与周向变形的最大值比径向变形大1～2个数量级。与之相对的螺旋桨的纵倾变化、侧斜变化以及螺距角的变化均随着进速系数的增加而减小，这也与前面所作的分析一致。

4 结 论

本文以DTMB P4381模型桨为研究对象，对所构建的螺旋桨流固耦合方法进行了分析验证。由验证结果可知，当计算同一金属材料螺旋桨时，本文所构建的FSI方法在低进速下计算所得结果要较传统CFD方法更为准确，而在高进速时，两种算法结果相对差别较小，这也与螺旋桨低进速重载状态下，叶片变形较大的的计算结果相吻合，从而从多角度验证了本文构建的螺旋桨流固耦合方法的可靠性。

［1］ Mouritz, Gellert E, Burchill P, et al.Review of advanced composite structures for naval ships and submarines ［J］ .Composite Structures, 2001, 53：21-41.

［2］ 黄胜，王超，王诗洋.不同湍流模型在螺旋桨水动力性能计算中的应用与比较 ［J］.哈尔滨工程大学学报，2009（5）：484-485.

［3］ Lin H J，Lin J J.Nonlinear hydro-elastic behavior of propellers using a finite-element method and lifting surface theory ［J］.Journal of Marine Science and Technology,1996（1）：114-124.

［4］ Young Y L.Fluid-structure interaction analysis of flexible composite marine propellers ［J］.Journal of Fluids and Structures, 2008, 24： 799-818.

［5］ Young Y L.Time-dependent hydroelastic analysis of cavitating propulsors［J］.Journal of Fluids and Structures,2007, 23 （2）： 269-295.

［6］ 孔为平，王金宝，冯学梅.螺旋桨敞水性能数值预报方法研究 ［J］.船舶，2012（6）： 13-21.

［7］ 李巍，王国强，汪蕾.螺旋桨粘流水动力特性数值模拟［J］.上海交通大学学报，2007（7）：1200-1203.

［8］ 张帅，朱锡，侯海量.船舶螺旋桨流固耦合稳态求解算法 ［J］.哈尔滨工程大学学报，2012（5）： 615-621.