船舶动力定位中的控制分配技术研究现状与展望
杨荣如
(海军驻上海地区舰艇设计研究军代表室 上海200011)
引 言
随着船舶设计的发展,人们为了获得更好的船舶操纵性能,在推力设备上采用了更高效的全回转推进器、吊舱推进器和喷水推进器等新一代推进转置。这样虽然可以有效提高系统的可靠性,但同时也为系统增加了更多的冗余度。对于这样的过驱动系统,“如何将控制系统得到的指令分配到各推进器上”是系统设计过程中需要考虑的一个重要问题。
对于船舶运动控制,通常安装多个可以实时产生变化的推力和转矩的执行机构,包括螺旋桨、舵、鳍等装置。本文研究在位置保持及特定轨迹航行条件下的控制分配问题,该种作业条件下,执行机构可为管道螺旋桨、全回转推进器、吊舱推进器和喷水推进器等装置。为了完成作业要求,通常船舶上安装多个推进装置,由它们共同产生控制器计算得到系统所需要的力和力矩。控制分配技术是完成控制量最优分配的最为有效的方法,文章将对该问题进行一般性描述,然后从线性和非线性两个方面进行讨论,介绍推力分配技术的最新研究成果,讨论该领域有待进一步研究的问题。
1 问题描述
考虑一般的反馈控制系统,其状态空间描述如下[1]:
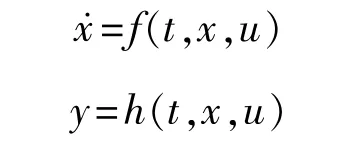
其中向量x表示船舶系统的状态,u为系统的输入。通常船舶控制系统设计过程中,首先不考虑具体执行机构的性能,而是从船舶的运动方程出发,根据扰动情况,设计出控制器,该系统的输入包括横荡力、纵荡力及艏摇力矩三个自由度,向量u可以表示为:
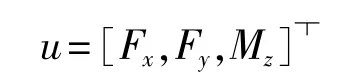
但是该组力和力矩则需要由若干个具体的推进器来实现,这样系统的状态空间变为以下三个方程:
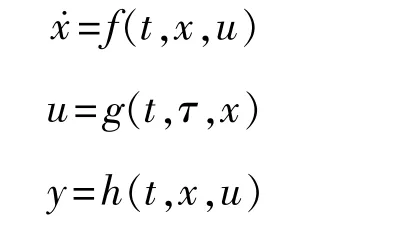
向量 表示推进器产生的推力向量,其具体形式与安装的推进器数量及种类有关。控制分配就是要完成的设计,通过其反函数
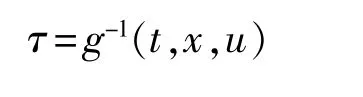
可以将控制器得到的船舶系统三自由度的力和力矩的输入,转化为具体推进器的输入,进而构成一个完成的控制系统。以上是船舶控制分配问题的一般性描述。
2 线性控制分配
2.1 解线性方程组
Morgan的专著最早涉及到船舶的推力分配问题[2]。他所研究的系统安装有3个推力方向固定的螺旋桨,产生的推力为 ,考虑到螺旋桨旋转方向可逆,各推力可以取负值。第1个螺旋桨布置在尾部,其余2个螺旋桨作为侧推。设3个推进器的x轴与推进器到船舶旋转中心连线的夹角分别为1,2,3,3推进器到旋转中心的距离为l1,l2,l3,由力和力矩的叠加原理可知[2]:
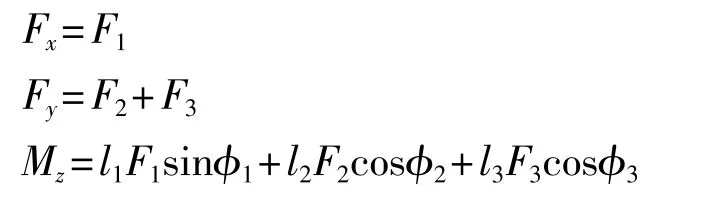
求解以上方程组,可得:
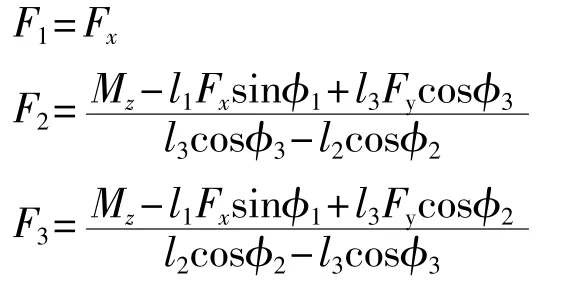
对于超过3台推力器的情形,也可按上述方式求解并平均分配在各推进器上。该分配方案中,推进器的方式是固定的,这样的方案并非能量最优,也没有考虑实际的工作海况。该种方法是船舶控制分配技术的最原始的形式,后来的各种方法是在该方式基础上考虑更为实际的工作状况而改进形成的,例如Wichers提出的分组分解法,这种方法是将多个推进器分成小组,首先根据指令在第1组推进器中进行分配,如果无法满足则再加入第2组推进器,这样依次迭代,直到满足条件后方可停止,但这样最后几组推力器往往得不到充分使用[3]。早期的这种方法只适用于推力方向固定的推进装置,如敞式螺旋桨、槽道螺旋桨等,该算法的使用范围也颇受限制,目前此种算法应用场合较少。
2.2 无约束伪逆算法
随着船舶特种装置的发展,全回转推进器逐步应用到船舶操纵中。对于一个全回转推进器,具有推力大小和方向两个变量,这使推力分配问题更加复杂,但这也为寻找最优推力分配方法提供了可能。广义逆分配算法,主要针对的是装有全回转推进器的船舶而提出的,其本质上采用L2范数近似描述系统消耗的总功率,作为该线性优化目标。该方案也是求解线性方程组的进一步发展。因为每个推进器变为2个输入变量,这样方程组含有无穷多解。伪逆算法就是要从中选取出最优分配方案[4]。
对于装有n个全回转推进器的船舶,设各个推力组成的推力向量为,各推进方向与x轴夹角组成向量为,每个推进器在船体坐标系中的坐标为(xi,yi)。由各个推进器产生的推力可以描述为:
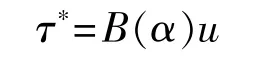
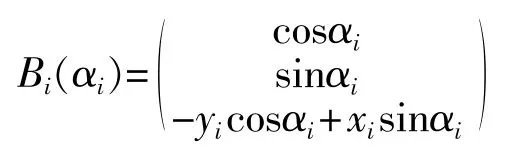
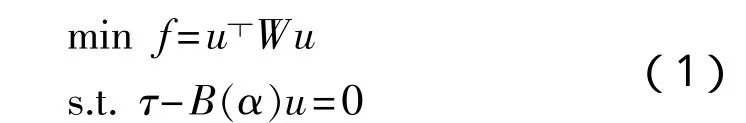
式中:W为正定矩阵,对于以上的约束优化问题,定义如下的拉格朗日函数:
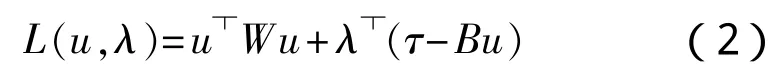
式中: 为拉格朗日乘子,可以得到拉格朗日函数倒数如下:
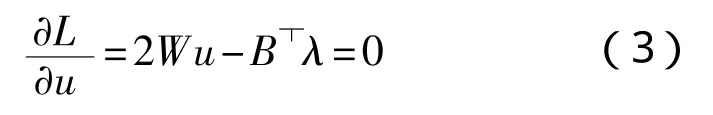
式中u满足:

将(4)带入(1),有
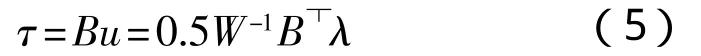
如果取W为单位阵,最后得到的在某一给定角度下,最优的推力方案为
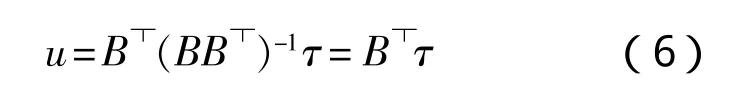
此方案相比求解线性方程组,可以找到能量消耗最优方案,而且求解方法简单。由于没有约束条件,无法对推进器的最大值加以限制,此外某些物理条件也限制了该方法的使用。
2.3 约束线性优化
上述伪逆算法不能保证约束,即 (其中为可行域)。但是考虑输入的可行域,很有可能导致在可行域内无法找到一点满足 ,这导致控制分配算法产生一定的误差。Durham在1993年证明出在加入简单的饱和限制后,任何一个广义逆都不能保证任何情况下进行没有误差的控制分配。因为加入饱和条件后,系统误差不可避免,因此将误差纳入到优化问题的目标函数中。
首先要给定变量的可行域,可以用矩阵A和向量b表示如下:
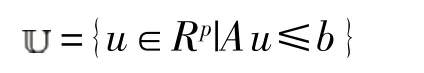
能量消耗可以采用1-范数或∞-范数进行表征,这样可以得到一个线性规划问题[5-6]。如果考虑1-范数情况,控制分配的目标函数如下:
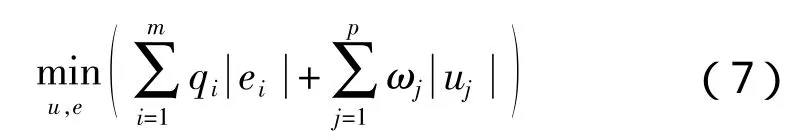
约束条件如下:
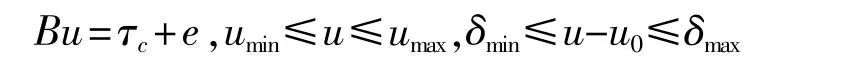
这样可以借助线性规划的一般算法进行求解,其优点是计算量小,可以快速完成控制分配的计算。此种算法及后续几种算法都是针对装有多个全回转推进器(或其他推力方向可变的推进器,如吊舱推进器)进行研究的,目前在水下航行器中,这些算法也有一定的应用[20]。
2.4 误差最优的二次规划
该种方法是与2.3中方法相对应的,也是考虑约束条件的线性优化方法,不同点是在目标函数中能量消耗与误差均采用L2范数进行描述,这使得问题可以采用数值二次规划的方法求解[7-9]。采用该种方法的控制分配可用如下目标函数描述:
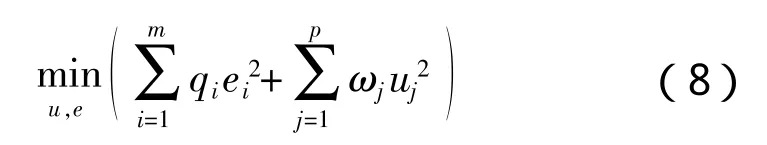
满足:
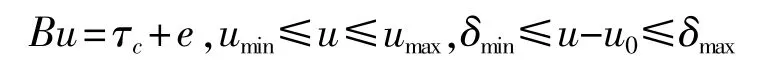
这个问题可以变成一个二次规划问题,如下:
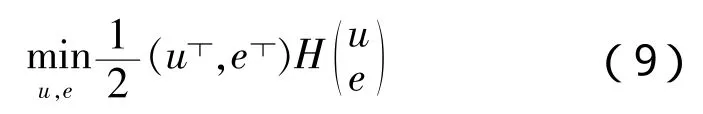
满足:
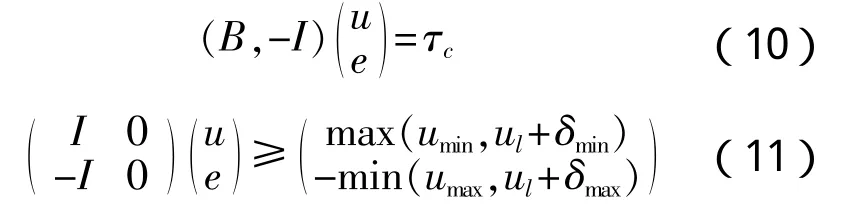
目前求解二次规划问题是非常方便的,Matlab中提供了直接基于二次规划求解控制分配的工具箱QCAT,目前也有C语言编写的软件。但是第2.3节和第2.4节中介绍的L1范数和L2范数都不是对船舶推进装置功率消耗状况最准确的描述[10]。
3 非线性控制分配
在非线性控制分配算法中,是一个非线性模型,这就使目标函数和约束条件可以含有非线性项。为了更为准确地描述控制分配过程,引入非线性算法是必要的,尤其是在线性模型很难近似的时变系统中。前面提到过,推力向量的L1范数、L2范数和L∞均很是对功率消耗的近似描述。对于螺旋桨及由其衍生出的推进器装置而言,其功率消耗P与转速n有如下近似关系[11,17]:

这为目标函数带来了很强的非线性。
3.1 序列二次规划算法
Johansen在2004年最早将序列二次规划方法应用到控制分配当中,在其模型中考虑了能源消耗、避免奇异结构,降低系统磨损等问题[12]。其基本模型如下[12,16]:

其中各项定义同2.2中定义的方法。系统中存在一种特殊的状态,就是 非满秩的时候,称之为奇异状态。在实际工作中,若系统陷入奇异状态,当控制信号发生较大变化时,各推力器无法在短时间合成所需要的力和力矩,此时系统不可控(这里的不可控不同于线性系统理论中所提到的不可控概念)。
此外全回转推进器在旋转过程中会产生较大摩擦,为了减小机械磨损,需要对各推进力方向的变化率加以限制,通常限制在1 °/s一下。
这样就可以得到一下优化模型:
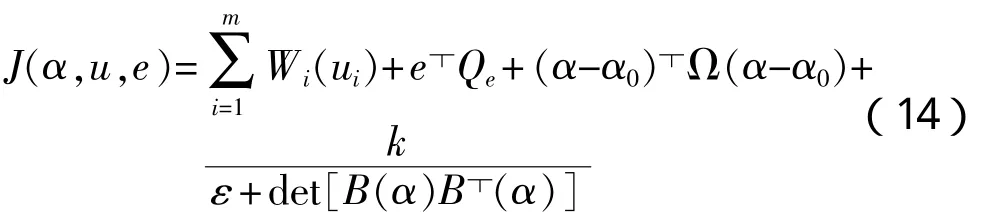
满足:
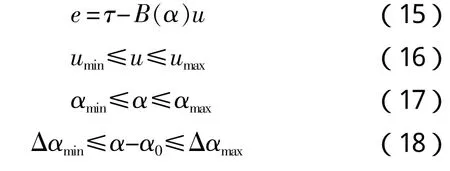
目标函数中第一项表示能量函数,第二项是误差,最后两项是对推力方向变化及奇异线性限制采用的罚函数,其中矩阵Q为正定矩阵。Johansen对此问题采用序列二次规划的方法进行求解,简要步骤如下:
(1)采用解析法或数值方式计算出目标函数J在 点的二阶泰勒展开。
(2)采用解析或数值微分的方法计算出F和G在 点的一阶泰勒展开。
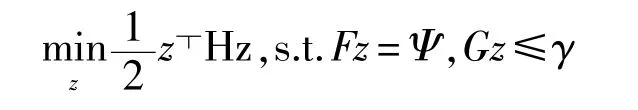
(4)求解二次规划问题,定义递推结果如下:
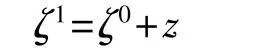
序列二次规划是工业界应用最为广泛的几种非线性优化算法之一,可以高效率地完成控制分配问题。但是若对于非凸函数,该种算法只可以取到局部最优点,而非全局最优点。
3.2 动态寻优方法
上面介绍的序列二次规划方法,属于静态求解控制分配问题。如果考虑时变情形,Lagrange乘子变为:
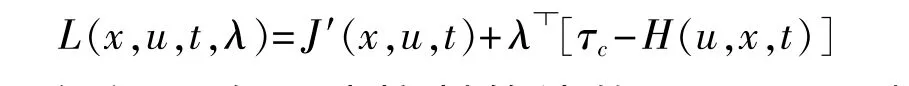
假设一个运动控制算法的Lyapunov函数存在,对于含有控制分配的Lyapunov函数可以定义如下:
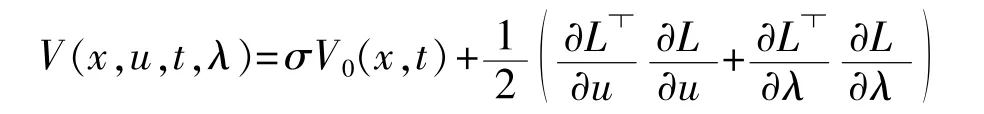
其中 。我们需要一个沿着跟踪轨迹的V具有负时间导数,这样可以得到一个控制分配算法如下:
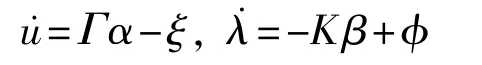
其中,和K为对称正定增益矩阵,和定义同 Johansen(2004)给出的方法[13-15]。
这种方法的优点是没有直接的数值优化算法而带来的庞大计算量。缺点是对于非凸的目标函数与约束条件,这种方法不一定总是收敛的。
3.3 智能分配算法
对于前面两种方法在某些条件下不能找到全局最优的缺点,智能优化算法也被应用到求解控制分配问题,例如遗传算法、粒子群算法等[20-21]。因为智能算法不需要借助目标函数的梯度信息,这样就可以设计更为接近系统实际情况的非凸函数、非光滑的优化模型。但是智能优化算法由于运算量庞大,往往不能满足控制分配实时性的要求,这就要求其进行离线计算,并制作出数据库,在实际工况下进行在线查询。
4 结 论
船舶动力定位中控制分配越来越受到人们的重视,利用控制分配技术,可以实现船舶控制器模块化设计,即对船舶总体的运动控制可以先只考虑船体的总体运动性能,而不考虑具体执行机构的性能,这样为船电系统设计带来极大的方便。目前使用最多的控制分配算法是伪逆算法与序列二次规划算法。传统方法在寻找能量最优解上存在一定的困难,近些年新兴的智能优化算法对寻找全局最优解提供了可能,但是其巨大的计算量也为实行分配带来了很大挑战,因此智能优化算法在控制分配问题中仍仅处于理论研究阶段。
对于未来控制分配算法,主要有以下几个方面的发展趋势:一是得到更接近全局最优解的优化算法,可以考虑将各种已有的控制分配方法结合起来,充分利用各种方法的优点[18-19];二是提高智能优化算法的收敛速度,这样方可以广泛用于推力分配的工程设计中来;三是充分考虑推力分配环节与系统整体的耦合问题,以改善系统的总体性能,这是一项极具挑战性的工作。
[1] Johansen T A.Optimizing nonlinear control allocation[C]//Decision and Control, 2004.CDC.43rd IEEE Conference on.IEEE, 2004, 4: 3435-3440.
[2] Morgan J.近海船舶的动力定位 [M].耿惠彬,译.北京:国防工业出版社,1984:188-201.
[3] Wichers J, Bultema S, Matten R.Hydrodynamic research on and optimizing dynamic positioning system of a deep water drilling vessel[C]//Offshore Technology Conference.Offshore Technology Conference, 1998.
[4] Durham W C.Constrained control allocation[J].Journal of Guidance, Control, and Dynamics, 1993 (4): 717-725.
[5] Bodson M.Evaluation of optimization methods for control allocation[J].Journal of Guidance, Control, and Dynamics, 2002 (4): 703-711.
[6] Bodson M, Frost S A.Control allocation with load balancing[C]//AIAA Guidance, Navigation, and Control Conference.2009: 10-13.
[7] Harkegard O.Efficient active set algorithms for solving constrained least squares problems in aircraft control allocation[C]//Decision and Control, 2002, Proceedings of the 41st IEEE Conference on.IEEE, 2002(2): 1295-1300.
[8] M.Petersen J A, Bodson M.Fast implementation of direct allocation with extension to coplanar controls[J].Journal of Guidance, Control, and Dynamics, 2002 (3): 464-473.
[9] Petersen J A M, Bodson M.Constrained quadratic programming techniques for control allocation[J].Control Systems Technology, IEEE Transactions on, 2006(1): 91-98.
[10] Fossen T I, Johansen T A.A survey of control allocation methods for ships and underwater vehicles[C]//Control and Automation, 2006.MED'06.14th Mediterranean Conference on.IEEE, 2006: 1-6.
[11] Fossen T I.Handbook of marine craft hydrodynamics and motion control[M].John Wiley &Sons, 2011.
[12] Johansen T A, Fossen T I, Berge S P.Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming[J].Control Systems Technology, IEEE Transactions on, 2004 (1): 211-216.
[13] Liao F, Lum K Y, Wang J L, et al.Adaptive control allocation for non-linear systems with internal dynamics[J].Control Theory &Applications, IET, 2010 (6):909-922.
[14] Liao F, Lum K Y, Wang J L, et al.Constrained nonlinear finite-time control allocation[C]//American Control Conference, 2007.ACC'07.IEEE, 2007: 3801-3806.
[15] Johansen T A.Optimizing nonlinear control allocation[C]//Decision and Control, 2004.CDC.43rd IEEE Conference on.IEEE, 2004, 4: 3435-3440.
[16] Liang C C, Cheng W H.The optimum control of thruster system for dynamically positioned vessels[J].Ocean Engineering, 2004 (1): 97-110.
[17] van Daalen E F G, Cozijn J L, Loussouarn C, et al.A Generic Optimization Algorithm for the Allocation of DP Actuators[C]//ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering.American Society of Mechanical Engineers, 2011: 87-94.
[18] Ji M, Yi B.The optimal thrust allocation based on QPSO algorithm for dynamic positioning vessels[C]//Mechatronics and Automation (ICMA), 2014 IEEE International Conference on.IEEE, 2014: 1365-1370.
[19] Yang I, Lee D.Networked Fault-Tolerant Control Allocation for Multiple Actuator Failures[J].Mathematical Problems in Engineering,2014(1):24-30.
[20] Sørensen A J.Dynamic Positioning Control Systems for Ships and Underwater Vehicles[J].Ocean Engineering,2014(1):84-88.
[21] Da-wei Z, Fu-guang D, Jin-feng T, et al.Optimal thrust allocation based GA for dynamic positioning ship[C]//Mechatronics and Automation (ICMA), 2010 International Conference on.IEEE, 2010: 1254-1258.

