一类含参Wilker型不等式的改进

何灯，郭晓辉，吴善和

（1.全国不等式研究会，浙江海宁314400；2.福清市元樵中学，福建福清350300；3.龙岩学院数学与计算机科学学院，福建龙岩364012）

一类含参Wilker型不等式的改进

何灯1，郭晓辉2，吴善和3

（1.全国不等式研究会，浙江海宁314400；2.福清市元樵中学，福建福清350300；3.龙岩学院数学与计算机科学学院，福建龙岩364012）

运用数值计算和分析方法，对一类含参Wilker型不等式作了改进，所建立的结论形式简洁且所得系数为最佳。

Wilker不等式；三角函数；双曲函数；改进

设x∈（0，π/2），则有著名的Wilker不等式［1］

文献［2-9］对式（1）的证明及加强做了大量探讨。

2007年，吴善和等［10］将式（1）拓广为：设λ，μ＞0，p≤2 qμ/λ，则当q＞0或q≤min｛-1，-λ/μ｝时，有

并得到如下Wilker型不等式

类比于文献［10］的结论，文献［11］建立了双曲函数的Wilker型不等式。

2009年，朱灵［12］得到Wilker型不等式下列推广结论。

（1）设0＜x＜π/2，当α≥1，有

第一个不等式成立当且仅当α＞0。

（2）设x＞0，当α≥1，有

第一个不等式成立当且仅当α＞0。

同年，朱灵［13］建立了含参双边Wilker型不等式：设0＜x＜π/2，当α≥1，双边不等式成立当且仅当η≤1/3，λ≥1-（2/π）α。当0≤α≤4/5，式（6）成立当且仅当λ≥1/3，η≤1-（2/π）α。当α＜0，式（6）右端不等式成立当且仅当η≥1/3。在文献［14］中，朱灵讨论了双曲函数的含参双边Wilker型不等式。

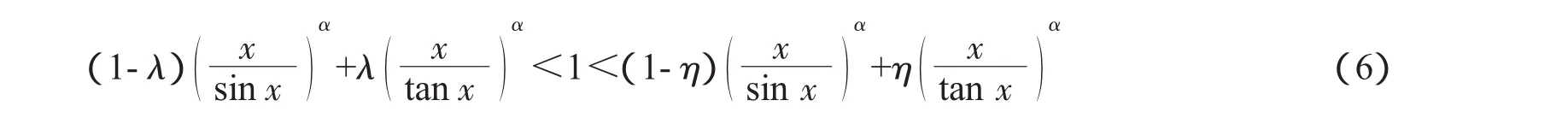
2013年，杨镇杭［15］研究了另一类含参Wilker型不等式，得到以下结论。

（1）设0＜x＜π/2，k≥1，则

（2）设x＞0，k≥1，则

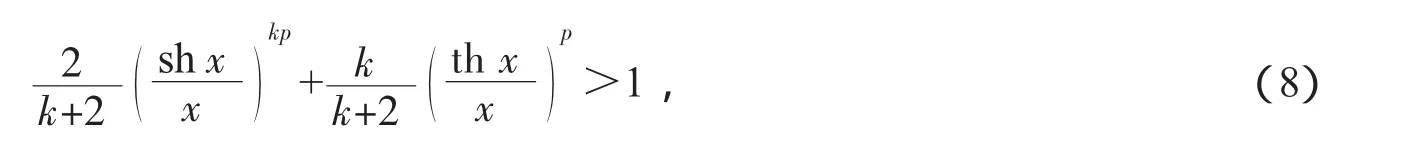
（3）设x＞0，k＜-2，则

在文献［15］的基础上，本文探讨式（7）的改进加强，得到以下定理。

定理设k、p＞0，x∈（0，π/2），则当140p2+42kp+588p+480≥35k2p2时，有

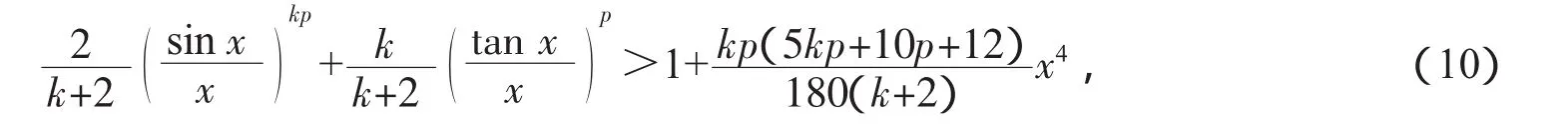
1　引理及证明

引理1当x∈（0，π/2）时，有

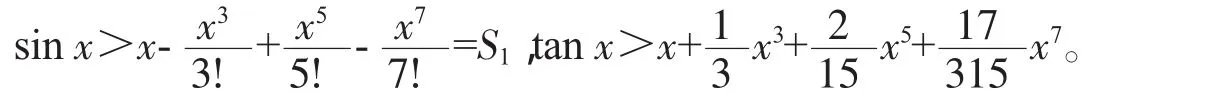
由Taylor级数展式易证，过程从略。

引理2［16］（1）当x＜0时，有

（2）当x∈R时，有ex≥

引理3当x∈（0，π/2）时，有

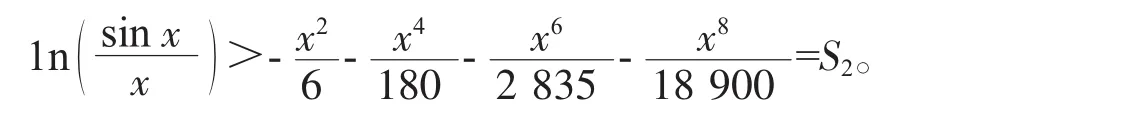
借助Maple数学软件整理，上述不等式等价于H1（x）＞0，其中

当x∈（0，π/2）时，有

综上，引理3得证。

引理5当x∈（0，π/2）时，有

证明首先证明当x∈（0，π/2）时，有

显然H（20）=0，由引理1得，则当x∈（0，π/2）时，H（2x）＞H2（0）=0。

综上，引理5得证。

结合引理5及引理2（2）可证引理6，证略。

2　定理的证明

借助于Maple数学软件整理得

其中

H4（x，kp）可看成关于kp的一元二次函数，注意到-16（2x6+20x4+315x2+9 450）3＜0，则此二次函数的图像开口方向向下，由140p2+42kp+588p+480≥35k2p2得

显然H4（x，0）＞0，经整理得

其中

注意到

则

其中

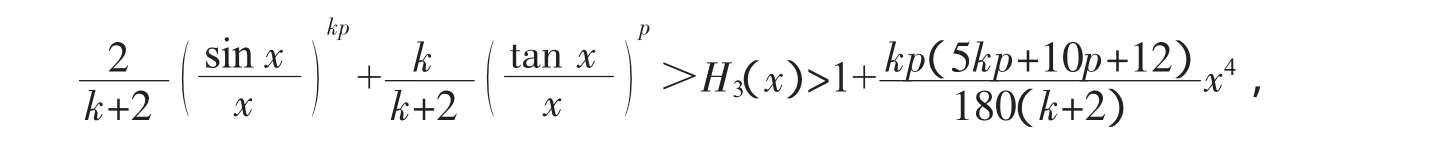
式（10）成立。

3　定理的应用

令定理中k=1，可得以下推论1。

推论1设p＞0，x∈（0，π/2），则

推论1改进了文献［13］建立的Huygens不等式的指数推广：设p＞0，x∈（0，π/2），则

将式（11）等价变形，可得以下推论2。

推论2改进了文献［10］建立的Sandor-Bencze型不等式：设p＞0，x∈（0，π/2），则

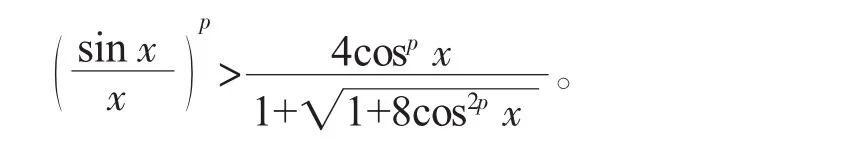
令定理中k=2，可得以下推论3。

推论3设p＞0，x∈（0，π/2），则

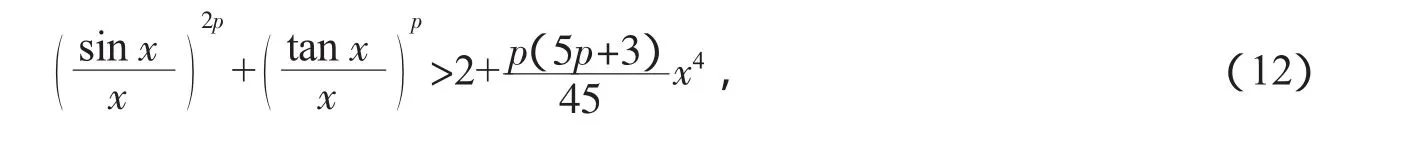
推论3改进了文献［13］建立的Wilker不等式的指数推广：设p＞0，x∈（0，π/2），则

将式（12）等价变形，可得以下推论4。

［1］WILKER J B.ProblemE3306［J］.The American Mathematical Monthly,1989,96（1）:55.

［2］陈超平,祁峰.关于Wilker不等式的两个新证明［J］.高等数学研究,2002,5（4）:38-39.

［3］刘爱启,王刚,李炜.含有三角函数的Wilker不等式的新证明［J］.焦作工学院学报,2002,21（5）:401-403.

［4］杨仕椿.关于Wilker不等式的一个加强［J］.阿坝师范高等专科学校学报,2003（3）:104-105.

［5］孙建设.含三角函数的Wilker不等式的两个简单证明［J］.高等数学研究,2004,7（4）:43.

［6］吴永锋,徐小松.关于Wilker不等式的简证与加强［J］.铜陵学院学报,2006,5（2）:72,88.

［7］ZHU L. A new simple proof of Wilker’s inequality［J］.Mathematical Inequalities＆amp;Applications,2005,8（4）:749-750.

［8］郭要红.Wilker不等式的两个新证明［J］.高等数学研究,2006,9（4）:79.

［9］ZHANGL,ZHUL.A newe lementary proof of Wilker’s inequalities［J］.Math Inequal Appl,2007,11（1）:149-151.

［10］WU Shanhe,SRIVASTAVA H M.A weighted and exponential generalization of Wilker’s inequality and its applications［J］. Integral Transforms and Special Functions,2007,18（8）:529-535.

［11］WU Shanhe,DEBNATH L.Wilker- type inequalities for hyperbolic functions［J］.Appl Math Lett,2012,25（5）:837-842.

［12］ZHU Ling.Some new Wilker-type inequalities for circular and hyperbolic functions［EB/OL］.［2009-05-11］.http://www.hindawi.com/journals/aaa/2009/485842/abs/.

［13］ZHU Ling.A source of inequalities for circular functions［J］.Computers and Mathematics with Applications,2009,58（10）: 1998-2004.

［14］ZHULing.Inequalities for Hyperbolic Functions and Their Applications［EB/OL］.［2010-05-15］.http://www.journalofinequalitie sand applications.com/content/2010/1/130821.

［15］YANG Zhenhang.Some sharp Wilker type inequalities and their applications［EB/OL］.［2013-04-19］.http://arxiv.org/abs/ 1304.5392.

［16］匡继昌.常用不等式［M］.4版.济南:山东科学技术出版社,2010.

【责任编辑：王桂珍foshanwgzh@163.com】

The improvement on parameter Wilker- type inequalities

HE Deng1,GUOXiao-hui2,WUShan-he3

（1.Chinese Society of Inequalities and Applications,Haining314400,China; 2.Yuanqiao Middle School,Fuqing350300,China; 3.Department of Mathematics and Computer Science,Longyan University,Longyan 364012,China）

An improvement on inequality is made by using computational and analytic techniques.The result is concise and the coefficient that we get is best.

Wilker- type lnequalities;trigonometric function;hyperbolic function;improvement

O122.3

A

1008-0171（2015）02-0060-06

2014-05-30

福建省自然科学基金资助项目（2012J01014）；福建省教育厅高校科研专项基金资助项目（JK2012049）

何灯（1984-），男，福建福清人，全国不等式研究会成员。