剪切流作用下隔水管涡激振动响应机理

毛良杰，刘清友，周守为,2，姜伟,2，刘正礼，彭涛

（1.油气藏地质及开发工程国家重点实验室（西南石油大学）；2.中国海洋石油总公司；3.中海石油（中国）有限公司深圳分公司；4.海洋工程国家重点实验室（上海交通大学））

剪切流作用下隔水管涡激振动响应机理

毛良杰1，刘清友1，周守为1,2，姜伟1,2，刘正礼3，彭涛4

（1.油气藏地质及开发工程国家重点实验室（西南石油大学）；2.中国海洋石油总公司；3.中海石油（中国）有限公司深圳分公司；4.海洋工程国家重点实验室（上海交通大学））

开展剪切流作用下隔水管涡激振动实验，分析剪切流作用下隔水管涡激振动特征参数及振动响应机理。实验中基于光纤光栅传感器测试技术采集剪切流作用下隔水管在流向和横向的涡激振动响应，实验数据处理时消除了实测信号中隔水管轴向预张力的影响并采用模态分析法求取隔水管位移响应。实验数据分析表明，剪切流作用下：隔水管不同位置处同一方向涡激振动响应频率一致；涡激振动锁定现象发生在涡泄频率对应的最大阶次固有频率附近且涡激振动受该阶次固有频率主导；受模态竞争的影响，剪切流涡激振动呈现多频响应形式；隔水管在流向的主导频率是横向主导频率的2倍；受相位角影响，实验中隔水管单个振动周期的运动轨迹呈扁斜“8”字形，多个轨迹重叠后呈“新月”形。图8表1参27

隔水管；剪切流；涡激振动；模态分析法；深水钻井

0 引言

深水钻井与陆地钻井的最大区别是钻具要通过从海上平台到海底井口长达数千米的隔水管[1-2]。隔水管在海洋结构中与采油生产立管一样属于细长柔性管柱，在海流作用下，隔水管两侧会形成交替的漩涡，漩涡的脱落会导致隔水管在流向（IL）和横向（CF）产生周期性的振动，即涡激振动（VIV）。

海流流速一般遵循从上到下随深度增加逐渐减小的规律，类似剪切流，因此，深水钻井过程中，隔水管受剪切流作用。目前国内外关于剪切流作用下隔水管涡激振动的研究较少：Jordan S K等[3-8]采用CFD（计算流体动力学）软件对剪切流作用下圆柱体涡激振动进行了初步研究；Kiya M等[9-13]开展了剪切流作用下的圆柱体涡激振动实验研究；黄智勇等[14-15]建立了理论模型并对剪切流作用下的立管涡激振动进行了初步分析；周守为等[16-17]完成了基于钻井工况与海洋环境耦合作用的隔水管力学行为实验，并获得了剪切流作用下隔水管的力学特性。根据以上研究现状可以看出，针对剪切流作用下的隔水管涡激振动实验研究还不足，且对剪切流作用下涡激振动机理认识有限。因此，本文基于光纤光栅传感器测试技术采集剪切流作用下隔水管涡激振动特性，利用模态分析法处理数据，获得剪切流作用下隔水管涡激振动特征参数，探索剪切流作用下隔水管涡激振动响应机理。

1 实验介绍

实验在上海交通大学海洋工程国家重点实验室深水试验池进行，水池长50 m、宽40 m，水深可在0～10 m自由调节。水池自带造流系统，可模拟均匀流、剪切流、暗流等各种类型海流。实验装置如图1所示。

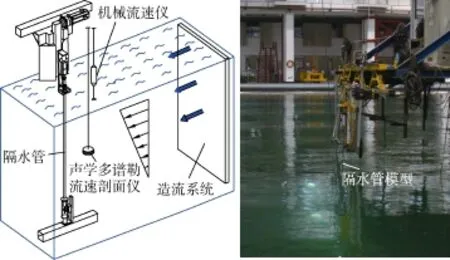
图1 实验装置图

1.1 剪切流模拟

根据深水试验池的造流能力，选择了表层流速为0.20 m/s、底层流速为0.05 m/s、从表层到底层流速基本呈线性递减的方式进行造流，即剪切流。在水中靠近隔水管模型处安装1个声学多谱勒流速剖面仪来测定隔水管模型附近的流剖面。由于声学多谱勒流速剖面仪不能测定表层流速，因此在水池表层安装1个机械流速仪来测定表层流速。实验开始前，通过2个流速仪校流并调整造流系统的参数，最终形成实验过程中剪切流流剖面（见图2）。

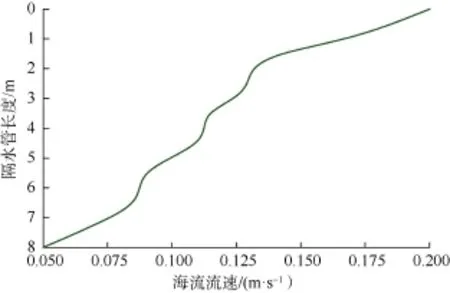
图2 实验模拟的剪切流流剖面

1.2 隔水管模型

目前，为了反映涡激振动特性，国外细长柔性管涡激振动实验模型以PVC（聚氯乙烯）管和玻璃钢为主[18-20]。本文隔水管模型采用定制的PVC管，表1为隔水管模型主要物理参数，其中固有频率由下式[13]计算得到：

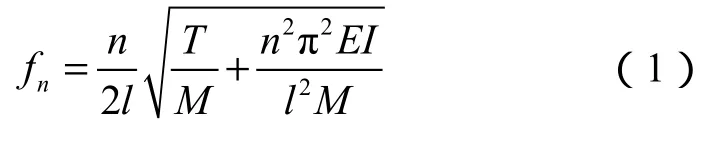
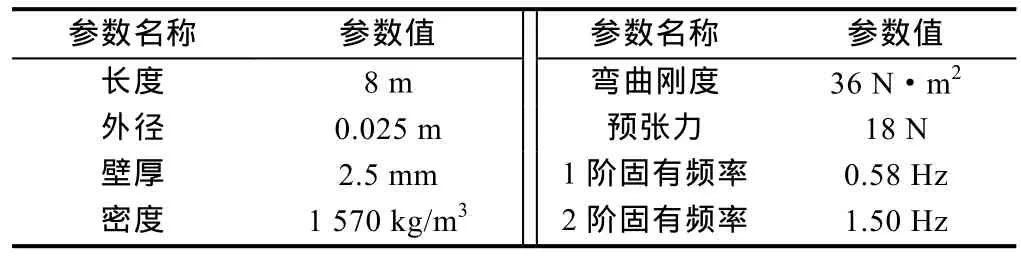
表1 隔水管模型主要物理参数

为保证实验中隔水管模型上下边界连接方式与实际深水钻井一致，隔水管模型上下边界采用万向节连接。

1.3 实验数据采集

光纤光栅传感器（见图3）具有体积小、测试数据准确等优点，布置于隔水管模型上不会对实验结果造成影响。De Wilde J J等[21]在Marin实验室的浅水拖曳水池中应用光纤光栅传感器测量了长细比（管长与截面回转半径之比）为787.5的立管模型的涡激振动响应，取得了良好的实验结果。本文实验采用定制的光纤光栅传感器采集数据。

图3 布置于隔水管模型上的光纤光栅传感器

隔水管表面有16个测点，从上至下依次记为测点1—测点16，测点1和测点16与隔水管上端距离分别为0.912 m和7.092 m，相邻测点间距均为0.412 m，每个测点四周对称分布4个光纤光栅传感器（见图4）。测点CF1与CF2用于测量CF方向的隔水管涡激振动特性，测点IL1和IL2用于测量IL方向的隔水管涡激振动特性。光纤光栅传感器的采样频率设定为250 Hz。实验时，先设置实验参数，待模拟剪切流稳定后，持续采集5 min以上的实验数据。

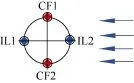
图4 测点周围光纤光栅传感器布置示意图

2 实验数据处理方法

2.1 波长与应变转换

实验过程中，光纤光栅传感器直接测量得到的是光信号波长，首先需要将波长转化为隔水管微应变，转换关系[22]为：

2.2 预张力影响的消除

隔水管发生涡激振动时，在漩涡的影响下隔水管在IL方向和CF方向周期性振动，引起隔水管轴向张力周期性变化，则CF方向测量的应变包含两部分：预张力引起的轴向应变和涡激振动引起的轴向应变。因此，必须从实测信号中消除预张力的影响。

CF方向上传感器CF1、CF2测量的涡激振动引起的轴向应变大小相等、方向相反，预张力引起的轴向应变大小相等、方向相同，因此，CF方向涡激振动引起的轴向应变为：

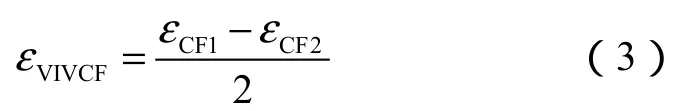
在IL方向，由于海流的作用隔水管会产生由拖曳力引起的初始轴向应变，在此基础上再产生周期性的涡激振动。因此，IL方向测量的应变包含3部分：预张力引起的轴向应变、初始拖曳力引起的轴向应变和涡激振动引起的轴向应变。则传感器IL1、IL2测量的轴向应变分别为：

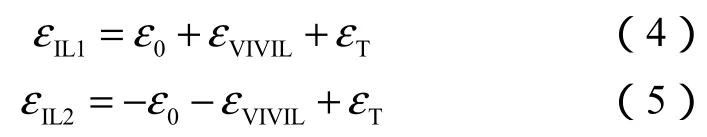
稳定的时间段内，可认为涡激振动引起的轴向应变时间历程均值为零，即，则由（4）式、（5）式可得：

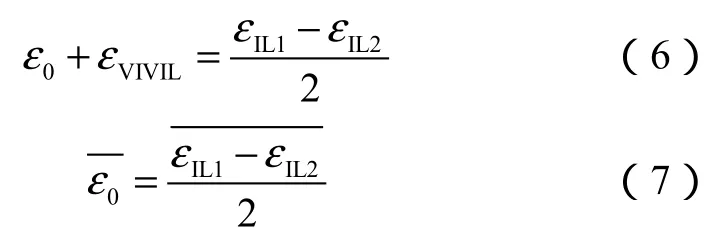
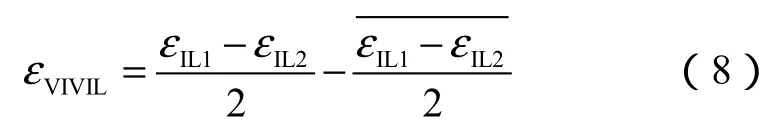
2.3 模态分析法

海流作用下，隔水管会产生IL和CF两个方向的振动，两个方向的模态分析法是一致的[23]，本文以IL方向为例说明数据处理的模态分析法。假设在时间域内隔水管轴线在IL方向的位移可表示为：

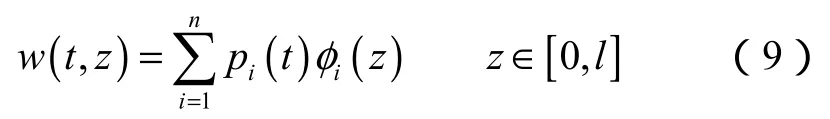
考虑隔水管作小变形运动，则隔水管模型轴线在IL方向的曲率为：

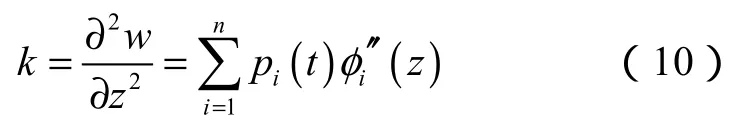
对于两端简支轴向力恒定的隔水管模型，其轴线在IL方向位移的模态振型是正弦的，即：

将（11）式代入（10）式，可得：

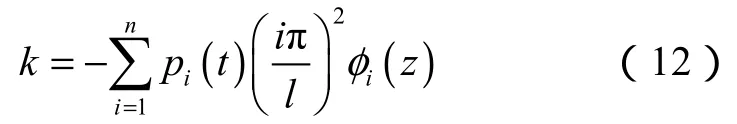
隔水管轴线IL方向曲率与同一轴向位置隔水管表面IL方向的轴向应变有如下关系：

结合（12）式、（13）式可得：

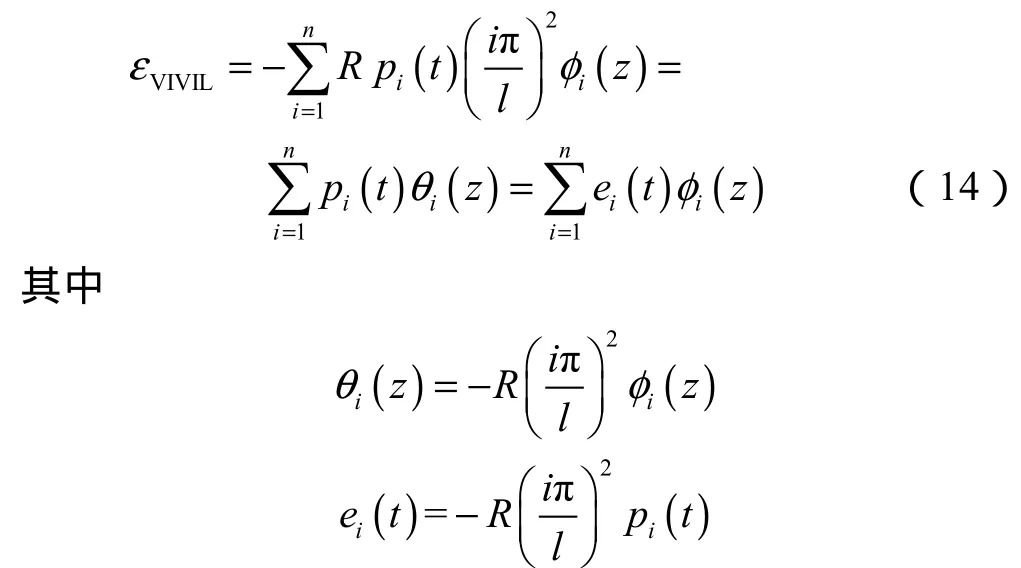
上述过程即为由隔水管表面应变信号求得隔水管位移响应的模态分析法，即已知隔水管表面各测点的应变时间历程之后即可获得其位移时间历程。

3 实验结果与讨论

由于隔水管上光纤光栅传感器采用等间距方式布置，所反映的规律基本一致，因此选择测点4、8、13进行分析。此外，引入折合速度对模拟的海流流速进行无量纲化处理：

3.1 位移标准差空间分布

位移标准差空间分布能够反映隔水管在海流作用下发生涡激振动的振型与主导模态，可通过对位移时间历程求标准差获得。图5为本文实验中隔水管IL与CF方向位移标准差空间分布，可以看出，IL和CF方向隔水管振动的模态阶次均为1阶。这是因为，本文实验中剪切流表层流速为0.20 m/s，海底流速为0.05 m/s，由Strouhal关系[24]（）可知，对应的涡泄频率为0.36～1.44 Hz，而隔水管模型1阶固有频率为0.58 Hz，2阶固有频率为1.50 Hz。因此，在本文实验条件下，模拟海流与隔水管模型相互作用形成漩涡，涡泄频率低于隔水管模型的2阶固有频率，则隔水管的主导模态最高为1阶。

3.2 应变时间历程

图6为测点4、8、13的应变时间历程，可以看出，测点8的应变幅值比测点4和测点13的应变幅值大。这说明本文实验条件下，隔水管靠近中间位置处应变幅值最大，与图5所示的隔水管位移标准差空间分布一致。这是因为，隔水管的振型即形变特征决定了应变幅值。本文实验条件下隔水管涡激振动由1阶模态主导，将以图5所示的振型在CF与IL方向周期性振动，在每个振动周期中，中间位置附近的变形均最大。

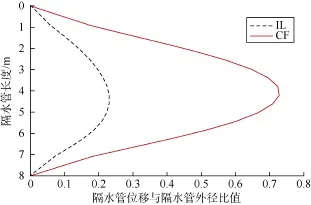
图5 隔水管位移标准差空间分布

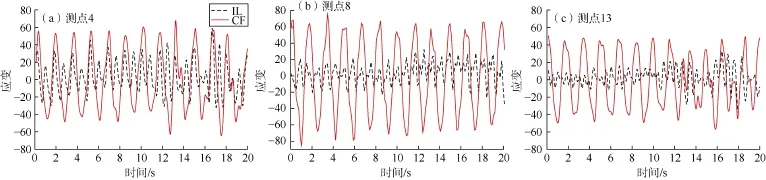
图6 隔水管测点4、8、13的应变时间历程

3.3 响应频率

对应变时间历程做快速傅里叶变化（FFT）即可获得相应的涡激振动响应频率谱。图7为图6所对应的涡激振动响应频率谱，可以看出：3个测点同一方向涡激振动响应频率是一致的，CF方向的主导频率均为0.6 Hz，IL方向的主导频率均为1.2 Hz。相关研究表明，均匀流作用下的涡激振动主导频率与海流速度引起的涡泄频率一致[24]。而本文实验模拟的海流是剪切流，测点4、8、13对应的流速分别为0.13 m/s、0.11 m/s、0.09 m/s，根据Strouhal关系[24]可知3个测点对应的涡泄频率分别为0.936 Hz、0.792 Hz、0.648 Hz，即剪切流作用下隔水管的涡泄频率沿管长方向分布是不均匀的，而3个测点CF方向的主导频率均为0.60 Hz，与隔水管1阶固有频率（0.58 Hz）非常接近。相关研究还表明初始拖曳力的影响以及涡激振动过程中张力周期性的变化会使隔水管固有频率小幅增加[13,24-26]，因此可以认为实验过程中隔水管CF方向涡激振动的主导频率与1阶固有频率一致。这说明剪切流作用下隔水管模型会以某阶固有频率振动而不受剪切流剖面的影响。这是因为，剪切流作用下隔水管涡泄频率沿管长方向分布不均匀，会发生模态竞争。本文实验条件下，涡泄频率接近1阶固有频率后，将发生涡激振动锁定现象，使隔水管振幅大幅增加并主导整个隔水管的振动，最终隔水管在CF方向将以1阶固有频率涡激振动。因此，剪切流作用下隔水管涡激振动锁定现象发生在涡泄频率对应的最大阶次固有频率附近且隔水管会以该阶次固有频率振动。

从图7还可以看出，剪切流作用下隔水管IL方向主导频率（1.2 Hz）是CF方向主导频率（0.6 Hz）的2倍，这与均匀流作用下不同方向响应频率间的关系一致。这主要是因为剪切流中某一段海流的涡泄频率与隔水管某阶固有频率接近之后，锁定现象发生，使隔水管以这一段海流引起的涡泄频率即某阶固有频率进行振动，这段海流漩涡脱落的方式决定了IL和CF方向的振动频率[22-24]。在锁定区域内，IL方向漩涡脱落1次振动1个周期，而CF方向漩涡脱落2次振动1个周期，由于剪切流作用下隔水管的振动受锁定区域振动频率主导，最终导致剪切流作用下IL方向主导频率是CF方向主导频率的2倍。此外，由于CF方向振动频率比IL方向振动频率低很多，因此CF方向振动频率会先接近隔水管的固有频率，从而出现涡激振动锁定现象，导致应变幅值大幅增加。

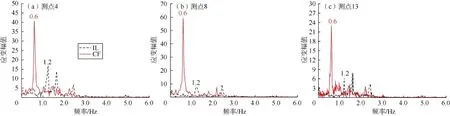
图7 隔水管测点4、8、13的涡激振动响应频率谱

均匀流作用下圆柱体涡激振动研究表明频谱曲线上存在来自不同方向间的干扰，这些干扰会以IL及CF方向主导频率上出现其他小尖峰的形式出现[23-24]。从图7可以看出，3个测点处的频谱曲线尽管主导频率突出，但出现了明显的锯齿状以及其他小尖峰，这些干扰并非IL和CF方向间的干扰所致，表明剪切流作用下隔水管涡激振动存在明显的多频现象。这是因为，尽管某阶固有频率附近的涡泄频率主导了涡激振动，但在模态竞争的影响下，其他频率下的漩涡泄放依然会作用于隔水管上，对隔水管涡激振动造成影响。

3.4 运动轨迹

均匀流作用下出现涡激振动时，由于IL方向主导频率是CF方向主导频率的2倍，细长柔性管的运动轨迹呈典型的“8”字形[24]。而在本文实验中，单个运动轨迹呈扁斜“8”字形，多个轨迹重叠后呈“新月”形（见图8）。这是因为：首先，本文实验中隔水管涡激振动由1阶固有频率主导且IL方向频率是CF方向频率的2倍，因此当隔水管在IL方向运动两个周期时在CF方向只运动了1个周期；其次，漩涡对隔水管存在IL方向的拖曳力和CF方向的升力，CF方向升力与CF方向间存在1个相位角，相位角的大小决定了隔水管运动轨迹的形状，而随着流速的变化相位角会发生变化。由（15）式及Strouhal关系可知，隔水管1阶固有频率对应的流速为0.1 m/s，对应的折合速度为6.1。由图8可知隔水管CF方向位移幅值为0.7D～1.2D。根据Jauvtis N等[27]建立的CF方向位移幅值-折合速度-相位角图版可知，本文实验条件下的相位角为45°～90°。因此，由于CF方向升力与CF方向间存在相位角，使CF方向升力的一部分作用在IL方向上，从而使平衡位置向左偏移，最终出现“新月”形的运动轨迹，而单个周期运动轨迹呈扁斜“8”字形。

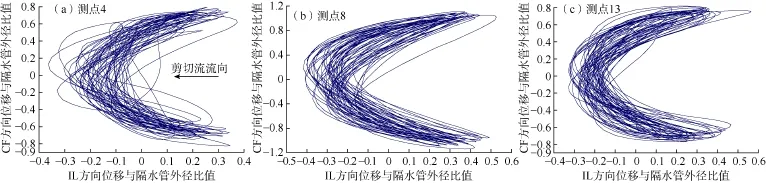
图8 隔水管测点4、8、13的运动轨迹

4 结论

本文开展了剪切流作用下隔水管涡激振动实验研究，对剪切流作用下隔水管涡激振动响应机理进行了初步探索，得到如下结论：剪切流作用下，主导模态决定了隔水管应变幅值、振型、响应频率；剪切流作用下隔水管不同位置处同一方向涡激振动响应频率是一致的；锁定现象发生在涡泄频率对应的最大阶次固有频率附近且隔水管会以该阶次固有频率振动；受模态竞争的影响，隔水管涡激振动存在多频现象；剪切流作用下依然存在隔水管IL方向主导频率是CF方向主导频率的2倍关系；受相位角影响，实验条件的剪切流作用下隔水管单个振动周期的运动轨迹呈扁斜“8”字形，多个轨迹重叠后呈“新月”形。

符号注释：

fn——n阶固有频率，Hz；n——振动阶次；T——预张力，N；M——静水中单位长度隔水管质量，kg/m；l——隔水管长度，m；E——管材弹性模量，Pa；I——管材截面惯性矩，m4；ε——隔水管微应变；λ——光信号波长值，nm；εVIVCF——CF方向涡激振动引起的轴向应变；εCF1——传感器CF1测量的轴向应变；εCF2——传感器CF2测量的轴向应变；εVIVIL——IL方向涡激振动引起的轴向应变；εIL1——传感器IL1测量的轴向应变；εIL2——传感器IL2测量的轴向应变；0ε——初始拖曳力引起的轴向应变；εT——预张力引起的轴向应变；的时间历程均值；的时间历程均值；的时间历程均值；t——时间，s；z——隔水管轴向坐标，m；w——隔水管轴线在IL方向的位移，m；i——模态阶次；φ——隔水管轴线在IL方向位移的模态振型；p——隔水管轴线在IL方向位移的模态权重；k——隔水管轴线在IL方向的曲率，m-1；R——隔水管半径，m；θ——关于曲率的模态振型；e——关于应变的模态权重；ur——折合速度；v——海流速度，m/s；D——隔水管外径，m；fs——涡泄频率，Hz；St——Strouhal数，取值为0.18[24]。

[1] 鞠少栋,畅元江,陈国明,等.深水钻井隔水管连接作业窗口分析[J].石油勘探与开发,2012,39(1): 105-110.Ju Shaodong,Chang Yuanjiang,Chen Guoming,et al.Envelopes for connected operation of the deepwater drilling riser[J].Petroleum Exploration and Development,2012,39(1): 105-110.

[2] 刘秀全,陈国明,畅元江,等.台风条件下深水钻井隔水管触底事故分析及对策[J].石油勘探与开发,2013,40(6): 738-742.Liu Xiuquan,Chen Guoming,Chang Yuanjiang,et al.Analyses and countermeasures of deepwater drilling riser grounding accidents under typhoon conditions[J].Petroleum Exploration and Development,2013,40(6): 738-742.

[3] Jordan S K,Fromm J E.Laminar flow past a circle in shear flow[J].Physics of Fluids,1972,15: 972-976.

[4] Tamura H,Kiya M,Arie M.Numerical study on viscous shear flow past a circular cylinder[J].Bulletin of the JSME,1980,23: 1952-1958.

[5] Yoshino F,Hayashi T.Numerical solution of flow around a rotating circular cylinder in uniform shear flow[J].Bulletin of the JSME,1984,27: 1850-1857.

[6] Wu T,Chen C F.Laminar boundary-layer separation over a circular cylinder in uniform shear flow[J].Acta Mechanica,2000,144: 71-82.

[7] Lei C,Cheng L,Kavanagh K.A finite difference solution of the shear flow over a circular cylinder[J].Ocean Engineering,2000,27: 271-290.

[8] Huang K,Chen H C,Chen C R.Vertical riser VIV simulation in sheared current[J].International Journal of Offshore and Polar Engineering,2012,22(2): 142-149.

[9] Kiya M,Tamura H,Arie M.Vortex shedding from a circular cylinder in moderate-Reynolds-number shear flow[J].Journal of Fluid Mechanics,1980,141: 721-735.

[10] Kwon T S,Sung H J,Hyun J M.Experimental investigation of uniform-shear flow past a circular cylinder[J].ASME Journal of Fluids Engineering,1992,114: 457-460.

[11] Hayashi T,Yoshino F,Waka R.The aerodynamic characteristics of a circular cylinder with tangential blowing in uniform shear flows[J].JSME International Journal: Series B,1993,36: 101-112.

[12] Sumner D,Akosile O O.On uniform planar shear flow around a circular cylinder at subcritical Reynolds number[J].Journal of Fluids and Structures,2003,18: 441-454.

[13] Lie H,Kaasen K E.Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow[J].Journal of Fluids and Structures,2006,22: 557-575.

[14] 黄智勇,崔维成,黄小平.均匀平面剪切流作用下圆柱体的涡激振动[J].哈尔滨工程大学学报,2007,28(12): 1301-1306.Huang Zhiyong,Cui Weicheng,Huang Xiaoping.Vortex-induced vibration of a cylinder in uniform planar shear flow[J].Journal of Harbin Engineering University,2007,28(12): 1301-1306.

[15] 林琳,王言英.剪切流作用下立管涡激响应的研究[J].船舶力学,2013,17(8): 901-910.Lin Lin,Wang Yanying.Research on vortex-induced vibration in linearly sheared flow[J].Journal of Ship Mechanics,2013,17(8): 901-910.

[16] 周守为,刘清友,姜伟,等.深水钻井隔水管“三分之一效应”的发现[J].中国海上油气,2013,25(6): 1-7.Zhou Shouwei,Liu Qingyou,Jiang Wei,et al.Theoretical and experimental study of deformation characteristics of deep-water drilling riser by ocean currents[J].China Offshore Oil and Gas,2013,25(6): 1-7.

[17] 刘清友,周守为,姜伟,等.基于钻井工况和海洋环境耦合作用下的隔水管动力学模型[J].天然气工业,2013,33(12): 6-12.Liu Qingyou,Zhou Shouwei,Jiang Wei,et al.A dynamic model of marine risers/pipes under the drilling operation condition and sea environment[J].Natural Gas Industry,2013,33(12): 6-12.

[18] Allen D W,Henning D L.Surface roughness effects on vortex-induced vibration of cylindrical strucures at critical and supercritical Reynolds numbers[R].OTC 13302,2001.

[19] 李琳,付世晓,杨建民.运动光纤光栅传感器的涡激振动测试技术[J].振动、测试与诊断,2011,31(6): 728-731.Li Lin,Fu Shixiao,Yang Jianmin.Measuring technique based on the fiber bragg used in the Vortex-Induced-Vibration model test[J].Journal of Vibration,Measurement &Diagnosis,2011,31(6): 728-731.

[20] Kang Zhuang,Jia Lusheng.An experiment study of a cylinder’s two degree of freedom VIV trajectories[J].Ocean Engineering,2013,70: 129-140.

[21] De Wilde J J,Huijsmans R H M.Laboratory investigation of long riser VIV response[C]//Proceedings of the Fourteenth International Offshore and Polar Engineering Conference.Toulon: The International Society of Offshore and Polar Engineering,2004.

[22] Marcollo H,Hinwood J B.On shear flow single mode lock-in with both cross-flow and in-line lock-in mechanisms[J].Journal of Fluids and Structures,2006,22(2): 197-211.

[23] Lie H,Kaasen K E.Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow[J].Journal of Fluids and Structures,2006,22: 557-575.

[24] Williamson C H K,Govardhan R.A brief review of recent results in vortex-induced vibrations[J].Journal of Wind Engineering and Industrial Aerodynamics,2008,96(6/7): 713-735.

[25] Williamson C H K,Roshko A.Vortex formation in the wake of an oscillating cylinder[J].Journal of Fluids and Structures,1988,2(4): 355-381.

[26] Allen D W,Henning D L,Li L.Performance comparisons of helical strakes for VIV suppression of risers and tendons[R].OTC 16186,2004.

[27] Jauvtis N,Williamsion C H K.The effect of two degrees of freedom on vortex-induced vibration at low mass and damping[J].Journal of Fluid Mechanics,2004,509: 23-62.

（编辑 胡苇玮 绘图 刘方方）

Vortex-induced vibration mechanism of drilling riser under shear flow

Mao Liangjie1,Liu Qingyou1,Zhou Shouwei1,2,Jiang Wei1,2,Liu Zhengli3,Peng Tao4
(1.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation (Southwest Petroleum University),Chengdu 610500,China;2.China National Offshore Oil Corporation,Beijing 100010,China;3.Shenzhen Company of CNOOC,Shenzhen 518067,
China;4.State Key Laboratory of Ocean Engineering (Shanghai Jiao Tong University),Shanghai 200240,China)

Vortex-induced vibration of the drilling riser under shear flow was studied by experimental method,and the characteristic parameters of vortex-induced vibration under the shear flow were obtained.The vortex-induced vibration response in both in-line and cross-flow directions were captured by measuring technique based on the fiber Bragg.The influence of the pre-tension during the experiment was eliminated and the experimental data was analyzed by modal analysis method.Results show that,under the shear flow,the dominant frequencies of the drilling riser at different locations are the same,however the shedding frequencies at different locations are different;when the vortex shedding frequency is close to the maximum order of the natural frequency,the lock-in phenomenon occurs,and the dominant frequency equals to this natural frequency;the vortex-induced vibration caused by shear flow is in the form of multi-modal for the influence of modal competition;the in-line direction response frequency is twice the cross-flow direction one;a single vibration period of the riser’s displacement trajectory appears as an inclined “8” shape,and the multiple vibration period of the riser’s overlapped displacement trajectory appears as a crescent shape.

drilling riser;shear flow;vortex-induced vibration;modal analysis method;deep water drilling

国家自然科学基金“基于钻井系统动力学的深海钻井升沉补偿系统机理研究”（51274171）；国家科技重大专项“深水油气井测试关键技术研究”（2011ZX05026-001-07）

TE52

A

1000-0747(2015)01-0101-06

10.11698/PED.2015.01.13

毛良杰（1987-），男，四川成都人，现为西南石油大学石油工程学院在读博士研究生，主要从事深水钻井工艺技术、细长柔性管柱涡激振动等方面的研究工作。地址：四川省成都市新都区新都大道8号，西南石油大学石油工程学院，邮政编码：610500。E-mail：maoliangjie@foxmail.com

联系作者：刘清友（1965-），男，重庆开县人，博士，西南石油大学教授，主要从事石油机械、油气井管柱力学与工具、计算机仿真等方面的研究工作。地址：四川省成都市新都区新都大道8号，西南石油大学，邮政编码：610500。E-mail：liuqy66@aliyun.com

2014-03-25

2014-12-17