深水钻井隔水管顶张力计算方法

杨进，孟炜，姚梦彪，高德利，周波，许云锦

（中国石油大学（北京）石油工程教育部重点实验室）

深水钻井隔水管顶张力计算方法

杨进，孟炜，姚梦彪，高德利，周波，许云锦

（中国石油大学（北京）石油工程教育部重点实验室）

通过隔水管受力分析，提出了既能保证隔水管稳定性又能满足底部过提力要求的深水钻井隔水管顶张力计算方法，以南中国海某超深水井为例对其进行验证，并与两种常用计算方法进行了对比。基于管柱力学原理，分析了真实轴向力与有效轴向力对隔水管力学行为的影响，结果表明：真实轴向力决定隔水管底部对隔水管总成的拉力，有效轴向力决定隔水管稳定性。通过隔水管在内、外压作用下的受力分析，建立相应的力学模型，推导出新的顶张力计算方法，弥补了美国石油协会（API）算法和法国石油学院算法的不足。现场应用实例分析结果表明：采用该方法计算的顶张力设置值与现场实际作业时顶张力值基本一致，且计算结果优于API算法及法国石油学院算法的计算结果，可以用于指导隔水管设计及施工。图5表1参11

深水钻井；隔水管；顶张力

0 引言

隔水管张力器通过为隔水管提供恒定的轴向拉力来控制其在水中的应力与位移，随着顶张力的增大，隔水管的弯矩与位移都会明显减少，但是应力会相应变大[1]。顶张力不足可能会使隔水管发生屈曲失稳，而顶张力过大则可能导致下部挠性接头失效，因此，准确计算隔水管顶张力对深水钻井作业有重要意义。

目前国内外就隔水管顶张力的认识并不统一，从而产生了不同的计算方法[2]。基于Sparks C P[3]提出的有效张力理论，形成了两种主流顶张力计算方法，即API（美国石油协会）算法和基于底部残余张力的算法。API算法规定，顶张力的设置应保证隔水管在水中的稳定性，即保证隔水管各部分的有效张力不小于零[4]。法国石油学院的Persent E等[5]则认为隔水管底部的有效张力即为残余张力。两种方法考虑均不全面，前者仅考虑了隔水管在水中的稳定性，而没有考虑现场作业对LMRP（下部隔水管总成）的过提要求；后者虽然考虑了LMRP的过提要求，但认为该过提力为有效张力施加而非真实张力施加。

在管柱轴向力方面，高德利等[6-7]把管柱轴向力分为有效轴向力和真实轴向力，并给出详细计算方法、物理意义及相互关系。本文基于管柱力学与弹性力学原理，通过隔水管在内、外压作用下的受力分析，考虑不同钻井液密度下的隔水管受力情况，建立隔水管顶张力的计算方程组，并通过现场实际应用对计算结果进行验证。

1 轴向力分析

以简单管柱（单一壁厚隔水管）在简单液压环境（管内外流体重率相同）下的情况为例进行隔水管轴向力分析（见图1）。

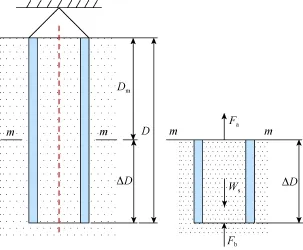
图1 简单管柱在简单液压环境下的受力分析

把管柱从任意断面m-m处截开，截断体受力分析如图1所示。

截断体重力为：

作用于截断体底面上的液压力为：

则根据受力平衡关系可得截断体轴向力为：

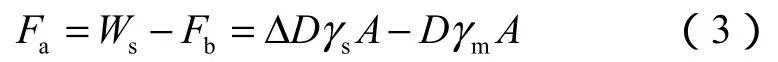
这就是压力面积法求管柱轴向力的基本原理。对（3）式进行整理可得[8-9]：

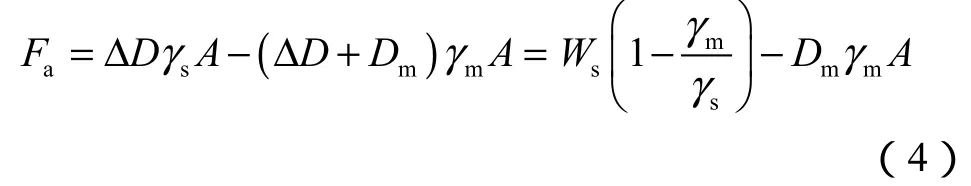
（4）式中，Fa为根据静力学平衡关系求得的真实轴向力，即为目前广泛使用的浮力系数，则为用浮力系数法求得的管柱浮重，也就是有效轴向力，DmγmA为虚力。由（4）式可知，有效轴向力等于真实轴向力和虚力之和。虚力对管柱的强度破坏和变形失效不起作用[7]，真实轴向力决定底部管柱对LMRP的拉力，但不能用于判定管柱的稳定性，有效轴向力决定管柱强度和稳定性[8]，也是判别管柱是否发生屈曲的依据。

2 隔水管力学模型

图2为隔水管的局部受力情况[10]。根据广义胡克定律和拉梅方程[11]，在实际作业时隔水管轴向除了受自身重力和液体对其产生的浮力外，外部海水产生的外挤力和内部钻井液产生的内压力也对其轴向力有一定影响。隔水管轴向受力体系可以分为管内液体对管壁的内压力、管外海水对管壁的外压力与隔水管本身所受的轴向力3部分进行分析。

图2 隔水管受力情况

在只考虑外压的情况下，隔水管所受外部压力可被海水对其的浮力作用所代替：

同理可得，在只考虑内压的情况下，隔水管所受内部压力可等效为内部钻井液的重力：

隔水管上下截面所受的外部压力均为人为施加，为了满足力的平衡关系，在轴向力的分析中需要减去这部分力，最终得到隔水管底部受力即有效张力[7-8]：

将以上3部分受力体系结合在一起即可得到隔水管的整体受力，对于隔水管整体，顶部没有内外压的影响。因此，隔水管整体受力平衡方程为：

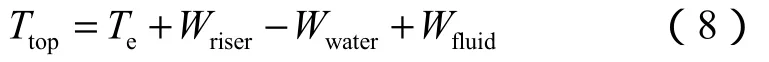
3 顶张力计算方法

根据API算法[4]，为确保隔水管在水中的稳定性，使其不发生屈曲失稳，应保证隔水管底部有效张力不小于零，则由（8）式可知：

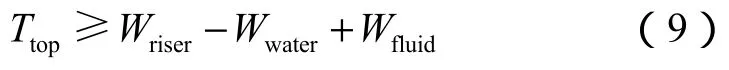
该方法没有考虑隔水管底部对LMRP的拉力，无法保证应急解脱时LMRP能快速安全地脱离防喷器。因此，实际作业时还需要考虑隔水管底部作用在LMRP上的拉力：

需要注意的是，实际作用在LMRP上的力为隔水管的真实张力Ttrue，而不是有效张力Te。这与法国石油学院提出的基于底部残余张力的算法[5]不同，该方法认为隔水管底部的残余张力为该处的有效张力，即：

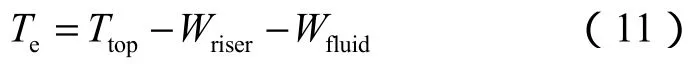
但是，真实轴向力才是与所有作用于管柱上的外力在轴向的分量相平衡的力[8]。所以，真正对LMRP起拉力作用的应为隔水管底部的真实张力。根据（7）式、（10）式，得到在保证隔水管不发生屈曲失稳的前提下，满足底部过提力要求所需增加的顶张力为：

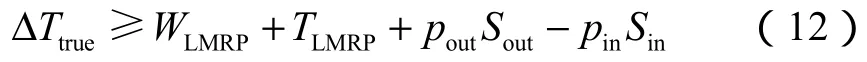
则结合（5）式、（6）式、（9）式、（12）式，得到既能保证隔水管稳定性又能满足底部对LMRP过提要求的顶张力计算方法应为：

在（13）式的基础上考虑因平台偏移而导致的隔水管倾斜，假设倾斜角度为θ，则：

4 应用实例

以南中国海某水深1 500 m的超深水井为例，其隔水管配置如表1所示。

根据现场作业实际需求，考虑底部过提LMRP 20 t，采用本文提出的计算方法得到顶张力随钻井液密度变化趋势（见图3）。由图3可知：钻井液密度达到1.800 g/cm3前，成功过提LMRP所需顶张力比不发生屈曲失稳所需顶张力大，则顶张力的设置应以前者为准；当钻井液密度达到1.800 g/cm3后，维持隔水管稳定性所需的顶张力更大，则顶张力的设置应以不发生屈曲失稳时所需顶张力值为准。

考虑隔水管在水中倾斜的情况，根据API规定，在连续钻井状态下隔水管下部挠性接头的最大转角为4°，将在水中的隔水管作近似线性处理，得到不同倾斜角下钻井液密度对顶张力的影响（见图4）。由图4可知：顶张力随着隔水管倾斜角度的增大而增大；钻井液密度较低时平台偏移对顶张力的影响较小，钻井液密度较高时平台偏移对顶张力的影响较大。因此，现场实际作业时，顶张力的设置应预留出相应的变化量，以保证平台偏移后顶张力满足要求。

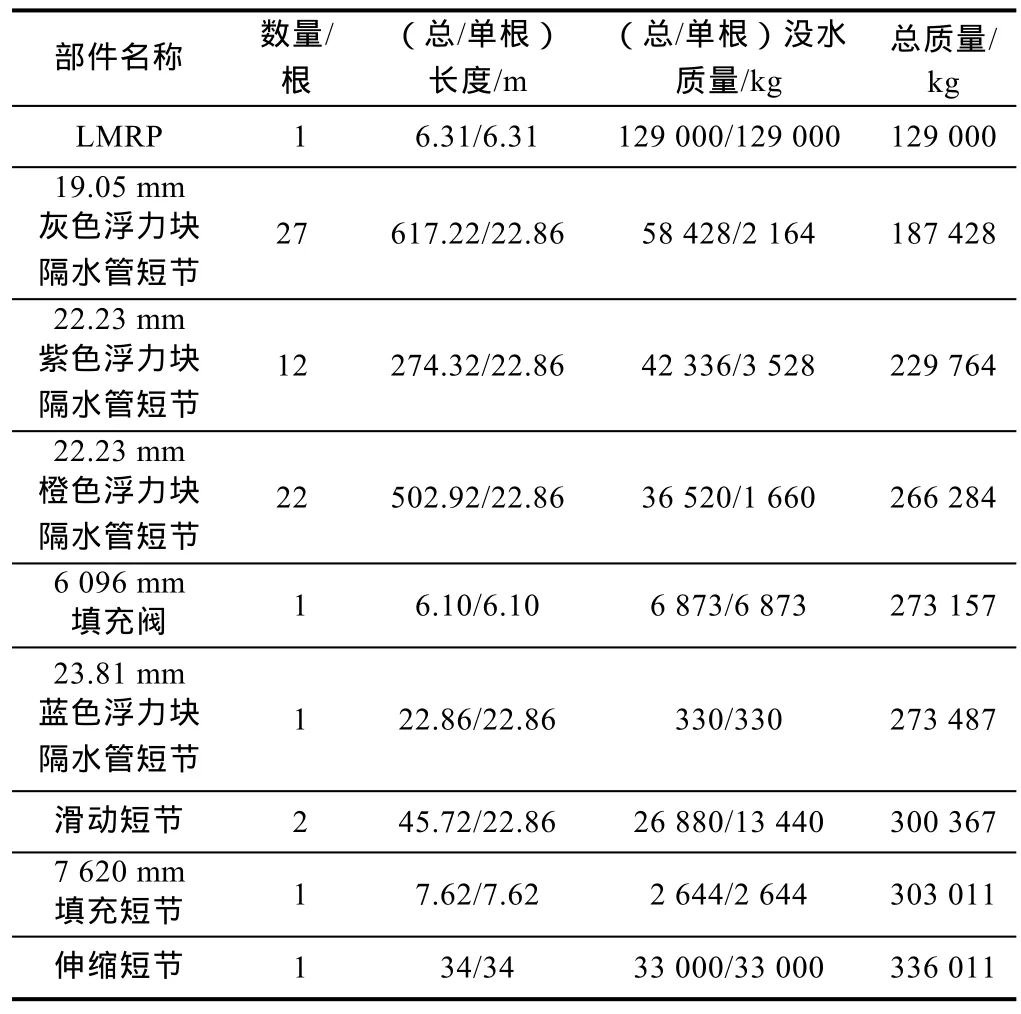
表1 隔水管配置表

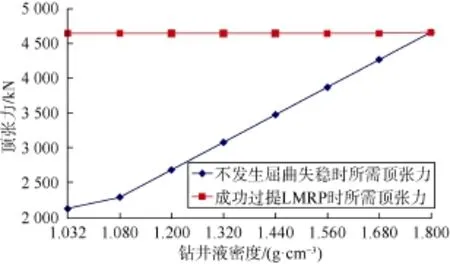
图3 顶张力随钻井液密度变化趋势

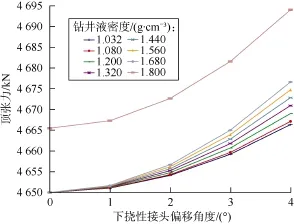
图4 隔水管倾斜时顶张力随钻井液密度变化趋势

取下部挠性接头转角为0°，分别使用API算法、法国石油学院算法及本文提出的算法进行顶张力计算，并对3种计算方法的结果进行比较（见图5）。由图5可知：在既考虑隔水管的稳定性又需底部过提LMRP 20 t时，采用本文方法计算的安装防喷器后顶张力设置值应为4 557 kN（约1025 kips），这与现场实际作业时的顶张力值（1 000 kips）基本一致；而API算法及法国石油学院算法的计算结果与现场实际作业时顶张力值有较大偏差。

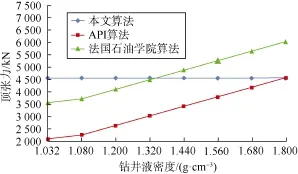
图5 不同计算方法顶张力计算结果对比

5 结论

本文基于隔水管受力分析，通过弥补API算法及法国石油学院算法的不足，并考虑平台偏移的影响，提出了新的深水钻井隔水管顶张力计算方法，既能保证隔水管稳定性又能满足底部对LMRP拉力要求。与API算法及法国石油学院算法相比，本文算法的计算结果与现场实际作业时顶张力值更加吻合，能够很好地指导深水钻井隔水管设计和现场施工作业。

符号注释：

ΔD——截断面距管柱底面的距离，m；D——管柱整体长度，m；Dm——截断面距管柱顶面的距离，m；γs——管柱管材重率，N/m3；γm——管柱内外液体重率，N/m3；A——管柱横截面积，m2；Ws——截断体重力，N；Fa——管柱轴向力，N；Fb——作用于截断体底面上的液压力，N；pout——隔水管外部液体压强，Pa；pin——隔水管内部液体压强，Pa；p1——浮力块上表面所受压强，Pa；p2——浮力块下表面所受压强，Pa；Ttrue——隔水管管壁所受真实张力，N；ΔTtrue——保证隔水管不发生屈曲失稳的前提下满足底部对LMRP拉力要求所需增加的顶张力，N；Wriser——隔水管自身重量与浮力块自身重量之和，N；Wwater——隔水管系统所受浮力，N；Wfluid——隔水管内钻井液总重量，N；L——隔水管长度，m；Sin——隔水管内横截面面积，m2；Sout——隔水管总横截面面积，m2；ρout——隔水管外海水密度，kg/m3；Wb——浮力块等体积排水重量，N；ρin——隔水管内部液体密度，kg/m3；g——重力加速度，m/s2；Te——隔水管有效张力，N； Ttop——隔水管顶张力，N；WLMRP——下部隔水管总成的没水浮重，N；TLMRP——实际作业时下部隔水管总成所需的过提力，N；θ——因平台偏移而导致的隔水管倾斜角度，（°）。

[1] 刘彩虹,杨进,曹式敬,等.海洋深水钻井隔水管力学特性分析[J].石油钻采工艺,2008,30(2): 28-31.Liu Caihong,Yang Jin,Cao Shijing,et al.Drilling riser mechanical characteristic of marine deep water[J].Oil Drilling &Production Technology,2008,30(2): 28-31.

[2] 鞠少栋,畅元江,陈国明,等.超深水钻井作业隔水管顶张力确定方法[J].海洋工程,2011,29(1): 100-104.Ju Shaodong,Chang Yuanjiang,Chen Guoming,et al.Determination methods for the top tension of ultra deepwater drilling risers[J].The Ocean Engineering,2011,29(1): 100-104.

[3] Sparks C P.The influence of tension,pressure and weight on pipe and riser deformations[J].Journal of Energy Resources Technology,1984,106(1): 46-54.

[4] American Petroleum Institute.API RP 16Q Recommended practice for design,selection,operation and maintenance of marine drilling riser systems[S].Washington D C.: American Petroleum Institute,1993.

[5] Persent E,Guesnon J,Heitz S,et al.New riser design and technologies for greater water depth and deeper drilling operations[R].SPE/IADC 119519,2009.

[6] 高德利,韩志勇.弹性钻柱两个特殊点的意义及计算方法[J].华东石油学院学报,1987,11(1): 1-10.Gao Deli,Han Zhiyong.The definition of two special points of drill string and calculation methods[J].Journal of East China Petroleum Institute,1987,11(1): 1-10.

[7] 韩志勇.垂直井眼内钻柱轴向力的计算和强度校核[J].石油钻探技术,1995,23(增刊): 8-13.Han Zhiyong.Study on axial force calculating and strength testing for drilling in vertical holes[J].Petroleum Drilling Techniques,1995,23(Supp.): 8-13.

[8] 韩志勇.液压环境下的油井管柱力学[M].北京: 石油工业出版社,2011.Hang Zhiyong.String mechanics in hydraulic condition[M].Beijing: Petroleum Industry Press,2011.

[9] 李子丰,蔡雨田,李冬梅,等.地层测试管柱力学分析[J].石油学报,2011,32(4): 709-716.Li Zifeng,Cai Yutian,Li Dongmei,et al.Mechanical analysis of pipe string in formation testing[J].Acta Petrolei Sinica,2011,32(4): 709-716.

[10] Sparks C P.Mechanical behavior of marine risers mode of influence of principal parameters[J].Journal of Energy Resources Technology,1980,102: 215-222.

[11] 杨桂通.弹塑性力学引论[M].2版.北京: 清华大学出版社,2004.Yang Guitong.Introduction to elasticity and plasticity[M].2nd ed.Beijing: Qinghua University Press,2004.

（编辑 胡苇玮 绘图 刘方方）

Calculation method of riser top tension in deep water drilling

Yang Jin,Meng Wei,Yao Mengbiao,Gao Deli,Zhou Bo,Xu Yunjin
(Key Laboratory for Petroleum Engineering of the Ministry of Education,China University of Petroleum,Beijing 102249,China)

Through mechanical analysis,a calculation method which meets the requirements of both the riser stability and the bottom overpull margin was deduced.It was verified by an example of ultra deepwater well in South China Sea,and compared with two other common methods.Based on the related theories of pipe string mechanics,the effects of true axial force and effective axial force on the riser mechanical behavior were analyzed.The results show that,the bottom tensile force to Lower Marine Riser Package is determined by true axial force,and the riser’s stability depends on effective axial force.Through the force analysis of riser which simultaneously bears the internal and external pressures,the correspondent mechanical model was established,and a new calculation method of top tension was derived,which remedies the deficiencies of algorithms proposed by American Petroleum Institute and Institute of French Petroleum.Field application shows that,the value of top tension calculated by this method is basically the same as the value set by field operation,and moreover,it is more accurate than the value obtained by the algorithms of American Petroleum Institute and Institute of French Petroleum.This method can be used to guide the design and operation of conductor.

deepwater drilling;riser;top tension

国家自然科学基金“海洋深水浅层钻井关键技术基础理论研究（51434009）”；国家自然科学基金“深水钻井表层导管喷射钻进机理研究”（51274215）；国家自然科学创新研究群体项目“复杂油气井钻井与完井基础研究”（51221003）

TE22

A

1000-0747(2015)01-0107-04

10.11698/PED.2015.01.14

杨进（1966-），男，河南周口人，博士，中国石油大学（北京）石油工程学院教授，主要从事海上钻完井技术的教学和研究工作。地址：北京市昌平区府学路18号，中国石油大学（北京）石油工程学院，邮政编码：102249。E-mail: cyjin1018@vip.sina.com

2014-06-28

2014-10-22