基于双同步旋转坐标的单/三相通用锁相算法设计
王汝泉,和军平,谭诗干,陈 力
(1.哈尔滨工业大学深圳研究生院,深圳518055;2.深圳市通业科技发展有限公司,深圳518000)
基于双同步旋转坐标的单/三相通用锁相算法设计
王汝泉1,和军平1,谭诗干2,陈 力2
(1.哈尔滨工业大学深圳研究生院,深圳518055;2.深圳市通业科技发展有限公司,深圳518000)
提出了一种新型单相/三相通用锁相环算法。该算法将单相电压、三相电压统一视为三相不平衡信号,在双dq同步旋转坐标系上进行投影,利用二倍频分量提取网络来实现正序信号、负序信号的快速解耦,有效提高了锁相环低通滤波器的截止频率;同时,利用正序直流d/q比值作为锁相环反馈量,克服了交流母线电压幅值变化的影响;同时还介绍了算法的结构和原理,建立了锁相环传递函数。考察了锁相环传递函数的零极点分布,分析了采样周期、低通滤波器截止频率对锁相性能的影响。最后,进行了仿真和实验,证明了该算法的有效性。
单相/三相通用锁相环算法;dq同步旋转坐标;二倍频分量提取网络
引言
锁相环技术PLL(phase-locked loop)是分布式发电设备并网、大功率变频驱动设备并联的关键技术之一,特别是交流母线电压波形存在较大畸变时,可靠、快速、准确的锁相技术对于变流装置并联非常重要[1-3]。目前,基于dq同步旋转坐标法的软件锁相技术可实现平衡三相电压下相位的准确提取,但当交流母线电压不平衡或畸变较大时,该方法的锁相精度与可靠性尚存在不足[4]。为此,文献[5,6]分别提出利用自适应陷波器ANF(adaptive notch filter)和滑动平均滤波器MAF(moving average filter)来减小电压不平衡、波形畸变的影响,但其抗扰能力受滤波器带宽的限制;文献[7]使用广义二阶积分器SOGI(second order generalized integrator)对电压基波和谐波中的正负序分量进行分离提取,再对基波正序分量闭环控制来实现锁相,但该方法需要产生额外的虚拟正交信号;文献[8,9]利用递归离散傅里叶变换、离散卡尔曼滤波器以提高锁相效果,但控制算法复杂、运算负担大。此外,通常的锁相算法仅适用于三相电网或单相交流母线,而在高速动车组变频传动、单/三相阻抗源变换器等应用场合,具有单/三相通用功能的可靠、高精度锁相算法也是很有必要的。
针对上述应用情况,本文提出一种抗扰、快速、精确的单相/三相通用的新型数字锁相算法。该算法将不仅适于三相电情景,当交流母线单相电网电压信号等效为三相电压不平衡的一种特殊状况,进而在dq双同步旋转坐标方法的基础上,利用二倍频分量提取网络,实现对基波正、负序信号的解耦控制和锁相。介绍了该单相/三相通用锁相环的原理和算法框图,并进行了建模仿真和实测验证。结果表明,该新算法改善了锁相的动静态性能,实现单相/三相两种电网电压下的可靠锁相。
1 单相/三相电压等效模型的双同步旋转坐标特性分析
交流母线中的三相电压通常以对称正序分量为主成分,工频正序分量在同步旋转坐标下表现为易分辨和处理的直流量,因而基于dq同步旋转坐标的三相电压软件锁相技术近年来得到了迅速发展[1-8]。而在高速动车组变频器并联驱动、单/三相阻抗源变换器等应用场合,进行可靠地单/三相通用锁相也很有必要。如将单相电网电压视为三相电压的一种特殊情况,即三相电压不平衡状况,就可在前述三相软件锁相的基础上,实现单相/三相电压可靠的锁相环设计,起到简化和通用设计的目的。
1.1 单相电压等效的三相不平衡电压模型
任一组三相正弦信号均可以分解为对称的正序分量、负序分量和零序分量,而单相电压信号实际上可等效为三相电压不平衡的一种特例。也即,将该单相电压作为A相,另两相B相、C相电压为零,就构成了一组三相不平衡电压。该三相不平衡电压可分解为正序分量、负序分量和零序分量,原理示意如图1所示。
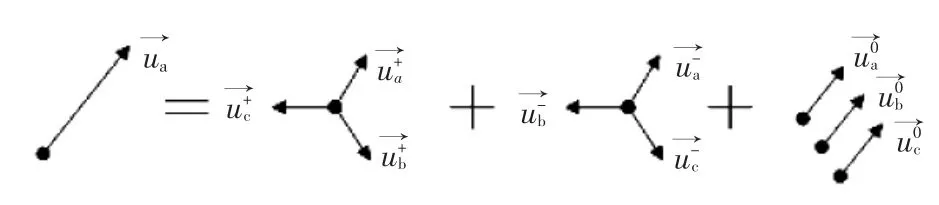
图1 单相电压等效的三相不平衡电压模型Fig.1 Three-phase unbalanced voltage model of single phase voltage

转化为方程组,即

解方程组,得

可见,该单相电压等效的不平衡三相电压的正序分量、负序分量、零序分量幅值相等。特别地,与相位也相同,这表明正序成分的A相分相电压信号与该单相电压信号时间相位一致。因此,如果能准确锁相住正序成分A相分相电压的相位,就实现了与该单相电压的同步。三相电网电压还有零序分量会影响到软件锁相的性能,为此,本算法先将三相电压求和,得到零序分量,再从三相电压中减去该零序分量,得到仅有正序、负序分量的电压成分,以利于锁相算法的后续处理,故本文忽略了零序分量。
1.2 双同步旋转坐标特性分析

图2 双同步旋转坐标系Fig.2 Double Synchronous Reference Frame


式中:φ+为矢量与d+轴的夹角;φ-为矢量与d-轴的夹角。则负序分量在同步旋转坐标系d-q-上投影的直流分量算式为
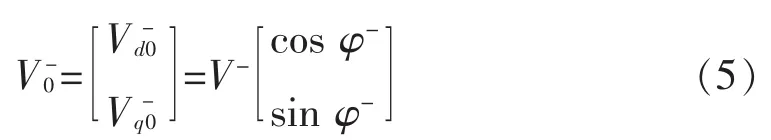
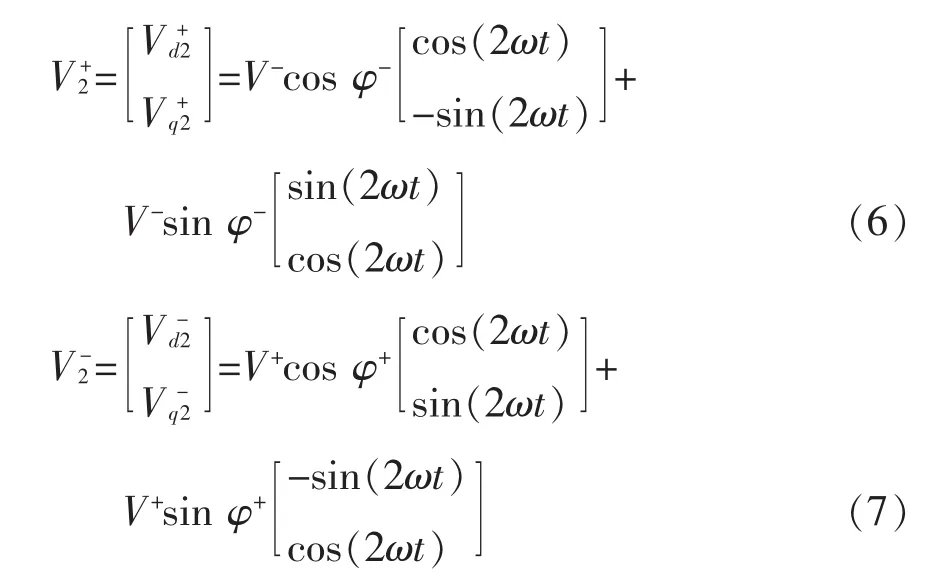
由此可见,电压矢量V在d+q+、d-q-坐标系中的投影由直流分量和二倍频交流分量组成。如用低通滤波器滤除二倍频分量,即可得到正序直流分量、负序直流分量。此外,由式(4)~式(7)可看出正负序直流分量与二倍频分量间也存在关联,如已得到正序直流分量和负序直流分量,二倍频分量也可由直流分量计算得到,即
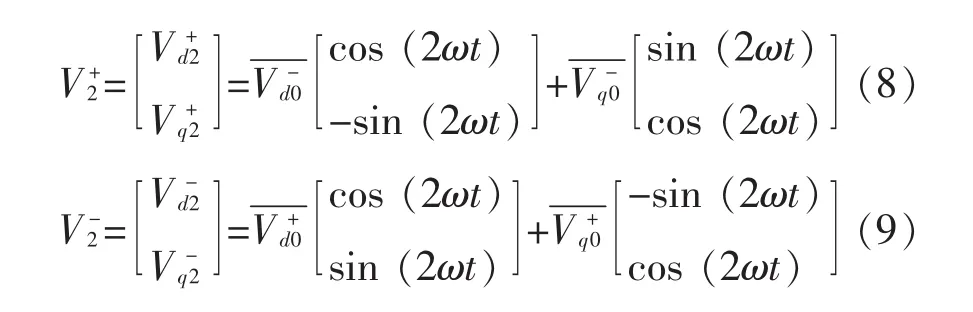
2 单相/三相通用锁相环结构及其改进算法
通常的同步旋转坐标软件锁相算法用较低截止频率的低通滤波器LPF(low pass filter)去滤除二倍频和高次分量,但截止频率较低会降低锁相环动静态性能。本通用锁相设计在双同步旋转坐标基础上引入两项改进算法,一是利用直流分量与二倍频分量间内在关系,构建了快速二倍频消除网络,大大提高滤波速度,提高锁相动静态性能;二是用正序同步坐标中的直流q/d比值为锁相环反馈量,以改善稳定性,克服电网电压幅值变化的影响。
2.1 二倍频分量提取网络设计
造成锁相环低通滤波器截止频率低的主要原因是同步旋转坐标中二倍频分量频率较低、幅值较大。如能在进入低通滤波器前,大大降低二倍频分量的幅值,就可以有效减缓对滤波器截止频率的要求。实际上,根据式(8)和式(9),二倍频分量也可由滤波后的直流分量计算而得,故构建出的二倍频分量提取网络[9]如图3所示。
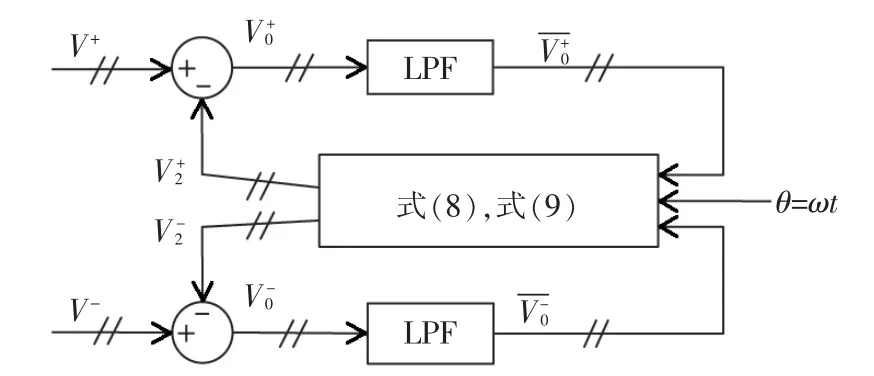
图3 二倍频分量提取网络Fig.3 Double frequency components extraction network
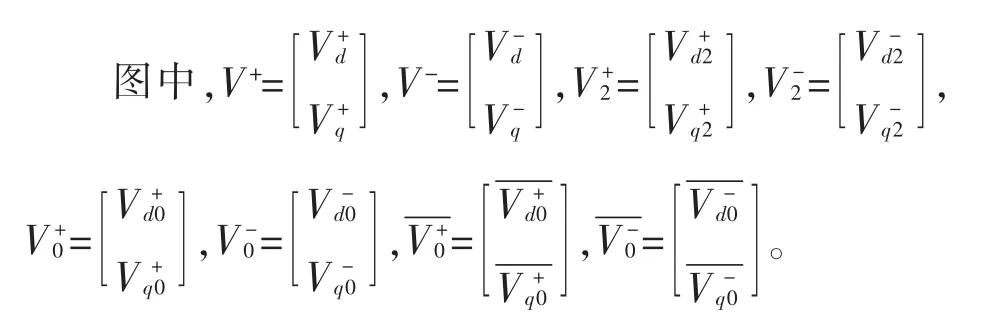
可以看出,该提取网络由2个小闭环算法构成。提取网络的输入量与反馈预估出的二倍频分量相减后,送给低通滤波器LPF滤波。这样有效缓解了对滤波器衰减量的要求,大大提高截止频率。
2.2 单相/三相通用锁相环算法
本文单相/三相通用锁相环算法的原理框图如图4所示,对于单相信号,将其转化为B相、C相信号为零值的等效三相不平衡信号。该设计使用双同步旋转坐标变换得到三相电压两个坐标系d+q+和d-q-的投影分量,采用二倍频分量提取网络估算出二倍频分量,在双同步旋转坐标系中减去估算出的二倍频分量,来实现对正、负序投影分量的快速解耦,再经低通滤波器LPF即获得两同步旋转坐标系中的各直流分量。则该低通滤波器的截至频率可大大提高。

图4 单相/三相两用锁相环控制框图Fig.4 Block diagram single-phase/three-phase phase-locked loop control
3 通用锁相环的模型分析与参数设计
为分析所提通用锁相算法的性能及进行参数优化设计,本文对该锁相环进行了建模分析和参数作用分析。设电网电压的输入相位为θin,锁相环的输出相位为θout,锁相环闭环模型如图5所示。

图5 锁相环系统模型Fig.5 Model of the designed PLL
图中LPF低通滤波器为二阶巴特沃斯滤波器,控制器数字采样等效为延迟环节,则可得到补偿前的锁相环开环传递函数,为

式中:ωc为低通滤波器截止频率;Ts为系统采样周期。为确定模型中各参数对系统动态、稳态性能的影响,本文用Matlab软件,对不同参数下系统开环传递函数的零极点分布进行分析。
3.1 低通滤波器截止频率对系统性能的影响
设采样时间Ts=10-4s不变,LPF的截止频率 fc由10 Hz逐步递增到100 Hz,系统开环传递函数的零极点分布变化如图6所示。可见,极点随滤波器截止频率增加而虚部更大,系统将有更高的振荡频率,不利于进入稳态;同时,过低的截止频率也将降低锁相的动态响应速度。本设计取fc=40 Hz作为LPF截止频率,来兼顾系统的动静态性能。
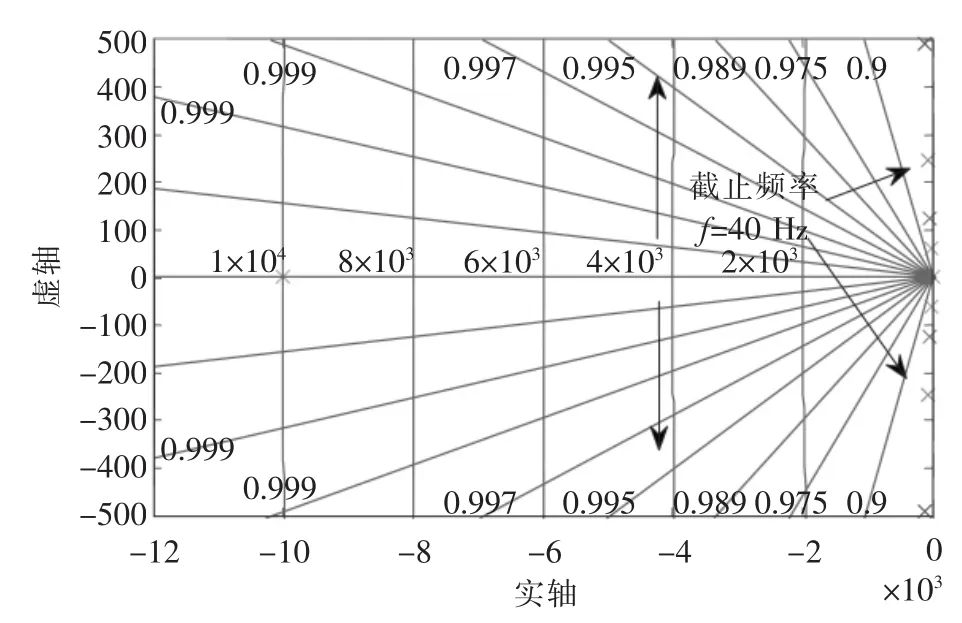
图6 系统零极点随滤波器截止频率变化趋势Fig.6 Variation tendency of pole-zero location with ωcchanging
3.2 采样周期对系统性能的影响
令截止频率fc为40 Hz,将控制器采样周期Ts从10-3s递减到10-5s,则开环传递函数的零极点分布变化如图7所示。可见,开环系统的极点随着采样频率的提高而有更大的负实部,系统将具有更快的动态响应性能。但控制器的采样频率不能无限增大,结合本锁相环的硬件情况,取采样周期Ts为10-4s。

图7 系统零极点随采样周期变化趋势Fig.7 Variation tendency of pole-zero location with the change of Ts
3.3 PI控制器参数设计
利用Matlab可对控制器的比例积分参数PI进行优化设计。针对前述系统开环传递函数零极点位置,本设计将PI控制器的极点选在原点,零点选在实轴上-14处,即得到系统PI控制器的参数为:Kp=26,Ki=410。
4 仿真与实验验证
为验证所提单相/三相通用锁相环算法及其效果,本文进行了仿真和实际测试。仿真在Matlab/ Simulink中进行,实物锁相器以TMS320F28335 DSP为核心,分别验证了三相电压输入、单相电压输入和波形畸变等时的锁相效果。
4.1 三相电网电压的锁相效果
令三相电网电压为平衡电压,其幅值为10 V、频率为50 Hz,本通用锁相算法对A相电压锁相的仿真结果如图8所示。由图可见,锁相算法准确地实现了锁相功能。
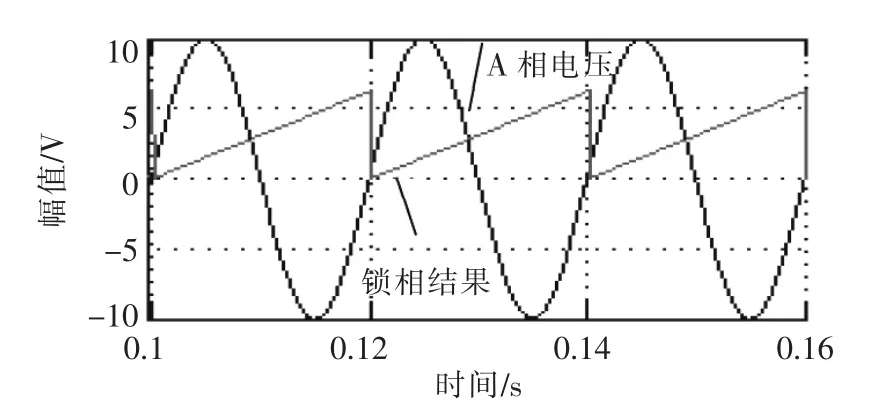
图8 锁相环对A相的仿真结果Fig.8 Simulation result of designed PLL to phase A
对三相电网电压的实际锁相效果如图9所示。图中,对比图9(a)的A相实际电压与图9(b)中锁相后得到相位对应的正弦值,其静态误差小于3%,可见锁相准确。

图9 实验验证锁相环对A相的锁相结果Fig.9 Experiment result of designed PLL to phase A
令三相电网电压为平衡电压,其幅值为10 V、频率为50 Hz,对比本文提出的单相/三相两用锁相环算法与文献[10]的锁相环算法的系统性能,对比结果如图10所示。由图可见,d轴分量和q轴分量的动态响应在三相输入情况下,两种算法的系统性能接近。
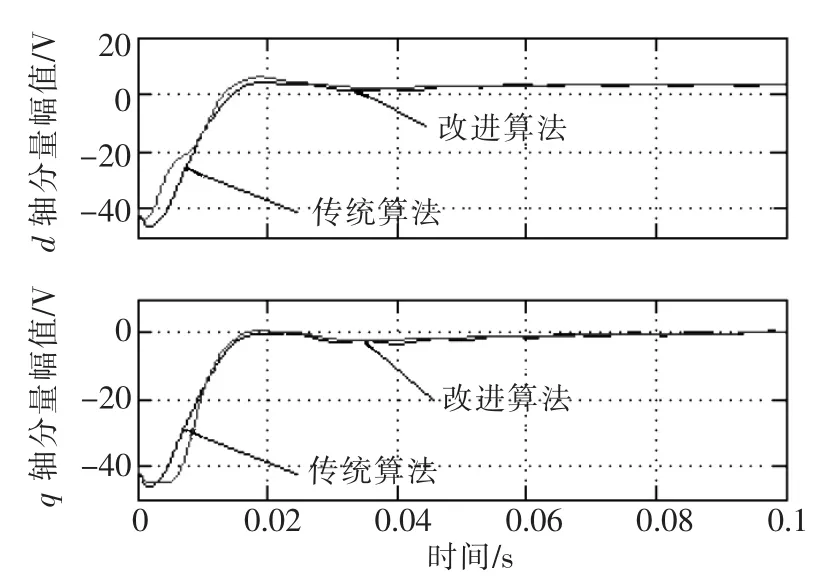
图10 两种算法的系统性能对比Fig.10 Comparison between two algorithms system performance
4.2 单相电网电压的锁相效果
令幅值为10 V、频率为50 Hz的单相电压作为被检测信号输入给锁相环算法的A相,同时令B相和C相的输入为0,仿真结果如图11所示。由图可以看出,该锁相环算法对单相电压也实现了准确锁相。
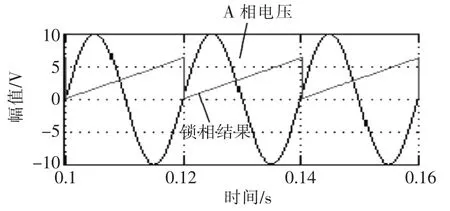
图11 锁相环对单相电压仿真锁相结果Fig.11 Simulation result of designed PLL to single phase
对该单相电压的实际锁相结果如图12所示,图中(a)为实际电压波形,图中(b)为锁相环得到的相位正弦值。由图可见,锁相是准确的。

图12 锁相环对单相电压实验锁相结果Fig.12 Experiment result of designed PLL to single phase
为考察本文所提的单相/三相两用锁相环算法的系统性能,本文利用仿真与文献[11]的锁相算法的性能进行对比。
令单相电压幅值为10 V、频率为50 Hz,上述两种算法的d轴分量、q轴分量的稳态精度如图13所示。由图对比可见,在单相电压输入情况下,即被检测信号输入给锁相环算法的A相,同时令B相、C相输入为0,本文所提的改进法的稳态精度明显要好于传统算法,同时新算法对d轴分量的动态跟随能力也有提高。

图13 改进算法与传统算法的对比Fig.13 Comparison of designed PLL and conventional PLL
4.3 锁相算法抗畸变能力
令三相电网电压为平衡电压,幅值为10 V、频率为50 Hz,电网中注入5次谐波和7次谐波,其幅值分别为2 V和1 V,分别验证在三相与单相情况下,本通用锁相算法对A相电压锁相情况,其仿真结果如图14所示。由图可见,本算法在恶劣电压工况下仍可实现锁相功能,准确地实现了锁相。

图14 电压畸变情况下锁相结果Fig.14 Result of designed PLL under voltage distorted
5 结语
本文设计了一种基于双旋转坐标的单相/三相通用锁相环算法。该算法将单相电压、三相电压统一视为三相不平衡信号,在双dq同步旋转坐标系上投影,利用二倍频分量提取网络来实现正序信号、负序信号的快速解耦,有效提高了锁相环低通滤波器的截止频率;同时,利用直流d/q比值作为锁相环反馈量,克服了电网电压幅值变化的影响。Matlab仿真和实际测试表明,本文提出的单相/三相通用锁相环算法是可行的,具有优良的动静态性能,可供交流并联变换装置设计人员参考。
[1]阚家荣,肖华锋,过亮,等.基于下垂锁相的逆变器并网控制策略研究[J].中国电机工程学报,2011,31(l8):21-26.Kan Jiarong,Xiao Huafeng,Guo Liang,et al.Study of control strategy for grid-connected inverters based on dropped PLL[J].Proceedings of the CSEE,2011,31(18):21-26(in Chinese).
[2]张志霞,朴在林,郭丹,等.一种应用于电力系统的锁相环[J],电工技术学报,2012,27(2):251-256.Zhang Zhixia,Piao Zailin,Guo Dan,et al.A Kind of Phase-Locked Loop for Power System[J].Transactions of China Electrotechnical Society,2012,27(2):251-256(in Chinese).
[3]王颢雄,马伟明,肖飞,等.双dq变换软件锁相环的数学模型研究[J].电工技术学报,2011,26(7):237-241.Wang Haoxiong,Ma Weiming,Xiao Fei,et al.Study of Model of Software Phase Locked-Loop Based on Dual-dq Synchronous Transform[J].Transactions ofChina Electrotechnical Society,2011,26(7):237-241(in Chinese).
[4]Frede B,Remus T,Marco L,et.al.Overview of Control and Grid Synchronization for Distributed Power Generation Systems[J].IEEE Transactions on industrial electronics,2006,53(5):1398-1409.
[5]Suzan E,Masoud K G,Alireza B.Enhancing the Three-Phase Synchronous Reference Frame PLL to remove Unbalance and Harmonic Errors[J],IEEE,2009,50(7):64-68.
[6]Eider R,Josep P,Salvador C,et al.Grid sequence detector based on a stationary reference frame[J].IEEE,2010,20(2):241-246.
[7]Pedro R,Alvaro L I C,et al.Multi-resonant frequencylocked loop for grid synchronization of power converters under distorted grid conditions[J].Chinese Journal of Ra-dio Science,2005,20(3):395-399.
[8]李明,王跃,方熊,等.无正交虚拟信号生成的单相DQ锁相环研究[J].中国电机工程学报,2011,31(15):1169-1174.Li Ming,Wang Yue,Fang Xiong,et al.Research on single-phase DQ phase-locked loop without imaginary signal generation[J].Proceedings of the CSEE,2011,31(15):1169-1174(in Chinese).
[9]Pedro R,Josep P,Joan B,et al.Decoupled double synchronous referecnce frame PLL for power converters control[J].IEEE Transactions on Power Electronics,2007,22(2):584-592.
[10]Minambres V,Milanés M I,Vinagre B,et.al.Comparison of controllers for a three-phase phase locked loop system under distorted conditions[J].IEEE Power Quality,Alternative Energy and Distributed Systems,2009:79-85.
Design of Single-phase/Three-phase Phase-locked Loop Algorithm Based on Double Synchronous Reference Frame
WANG Ruquan1,HE Junping1,TAN Shigan2,CHEN Li2
(1.Shenzhen Graduate School,Harbin Institute of Technology,Shenzhen 518055,China;2.Shenzhen Tongye Technical Development Co.,Ltd.,Shenzhen 518000,China)
An improved single-phase/three-phase phase-locked loop algorithm is proposed in this paper.This new algorithm treats the single-phase circumstance as a special unbalanced three-phase situation and then a three-phase phase-locked loop technology can be utilized and improved.In order to fast eliminate the coupled influence caused by positive sequence signal and negative sequence signal,a double frequency components extraction network is analyzed and built up for the double dq-synchronous reference frame PLL close-loop algorithm.This paper introduces the structure of this new algorithm and builds its transfer functions.The position variation tendency of the pole-zero points caused by sampling time and low-pass filter’s cut-off frequency is analyzed in detail and the analysis provide a direct guidance for PLL parameter design.In the end,simulation and experiment results verifiy the versatility,compatibility and effectiveness of this new phase-locked loop algorithm.
single-phase/three phase versatile phase-clocked loop algorithm;dq-synchronous reference frame;double frequency components extraction network
王汝泉(1986-),男,硕士,研究方向:电力电子与电力传动,E-mail:wangrq 1022@163.com;
和军平(1971-)通信作者,男,博士,副教授,研究方向:电力电子技术和电磁兼容,E-mail:hejunping@hitsz.edu.cn;
谭诗干(1975-),男,硕士,研究方向:电力电子技术,E-mail:shigan.tan@sztongye.com;
陈力(1982-),男,硕士,研究方向:大功率逆变电源技术,E-mail:li.chen@sz-tongye.com。
10.13234/j.issn.2095-2805.2015.1.7
:TM 46
:A
2014-08-11
国家留学基金(201206125059)
Project Supported by China Scholarship Council(201206125059)

