基于粒子群算法的非线性时变参数离散灰色预测模型

王 亮，滕克难，吕卫民，金永川

（1.海军航空工程学院a.七系;b.训练部，山东 烟台 264001；2.中国人民解放军 91681部队，浙江 宁波 315731）

0 引言

灰色系统理论是我国学者邓聚龙于20世纪80年代创立的一种处理“部分信息已知，部分信息未知”的“小样本，贫信息”不确定系统的理论，其中灰色预测建模技术是灰色系统最重要的内容之一，也是预测理论体系中一个新的研究分支[1]。GM(1,1)模型是灰色预测技术的基础模型，在其发展过程中得到了深入的研究，并有很多学者提出了不少改进方法，主要包括：残差修正法[1]、背景值构造法[2]、中心逼近法[3]、时间响应函数法[4]等。虽然这些方法在一定程度上提高了模拟与预测精度，但始终无法克服GM(1,1)模型利用离散方程进行参数估计，而利用连续时间响应方程进行预测造成的跳跃性误差。2005年，谢乃明[5]提出了离散灰色预测模型，将参数估计和预测模型统一为离散形式，有效地避免了由离散序列到连续方程造成的误差。之后有学者对DGM(1,1)模型进行了进一步的优化与改进。姚天祥等[6]针对经典DGM(1,1)模型的不足，研究了离散灰色模型选取不同初始迭代点的模拟数据增长率特点，并提出了两类分段修正离散灰色模型。刘卫锋等[7]通过选取三种不同修正形式初始迭代值，分别建立了三种优化离散灰色模型。李伟等[8]针对传统DGM(1,1)模型建模过程中假定原始数据序列服从近似指数增长规律，且以数据序列的第1个数据保持不变得出预测结果的缺陷，利用组合函数“对数—幂函数”对原始数据进行处理，使其符合灰色预测模型的建模规律，并引入遗传算法寻求离散灰色模型初始迭代值的最优解。但实际上传统的GM(1,1)与DGM(1,1)模型在工程应用中仍存在一些共同的缺陷与弊端。

本文分析了GM(1,1)及DGM(1,1)模型对数据要求上的限制，指出对于非定值增长的数据序列，GM(1,1)与DGM(1,1)模型的模拟及预测效果并不理想。考虑到系统行为发展的复杂时变性，为提高对各类型趋势数据的预测能力，引入非线性时间项，构造了一种拓展的非线性时变参数离散灰色模型（NTDGM(1,1)模型），利用粒子群算法（PSO）优化得到模型中各参数，并说明应用该模型进行建模和预测的步骤。最后通过实例比较该模型与其他模型的模拟及预测精度，结果显示本文模型对各类型趋势的数据模拟及预测均具有更高的精度。

1 GM(1,1)与DGM(1,1)模型的不足

由上式可知GM(1,1)模型的模拟数据是一个等比序列，数据序列的增长率为一个定值，而且由于在时间响应序列中假定了x(1)(1)=x(0)(1)，在应用中也会导致预测结果精确度不高。同时，由于样本数据初始值的改变不影响模型的发展系数和模拟值，因此，这也从某种程度上反映了初始值信息的损失。

GM(1,1)模型的离散形式，即离散灰色模型（Discrete grey model,DGM(1,1)）为

由上式可知，与GM(1,1)模型相同，利用DGM(1,1)模型计算的模拟序列增长率也是一个定值。而且与GM(1,1)模型一样，DGM(1,1)模型也假设x(1)(1)=x(0)(1)，这将导致初始值信息的丢失。

通过以上分析可知，无论是GM(1,1)还是DGM(1,1)模型的模拟值和预测值始终保持固定的增长率，因此这两个模型对近似指数规律的数据序列具有较好的模拟和预测效果。但在实际工程应用中，数据序列往往并不具备指数规律，两种模型的计算误差均较大。

2 拓展的非线性时变离散灰色预测模型

进一步分析DGM(1,1)模型可以看出，该模型中参数β是固定值，即表明DGM(1,1)模型适用于线性时不变系统的分析建模。但是在工程技术领域中，系统行为序列自身及不同行为序列间的相互作用导致系统输出序列呈现出复杂的非线性，而且系统随着时间的推移，其参数及结构也不断发生演化，因此利用恒定参数对现实系统行为进行模拟和预测是不合理、不科学的。为克服这种不足，本文将非线性时变参数引入，代替传统DGM(1,1)模型中的恒定参数，构造一种拓展的非线性时变参数灰色离散预测模型。

为拓展的非线性时变参数灰色离散预测模型（NT-DGM(1,1)）。

该模型主要由三部分构成：第一部分称作趋势项，为(β1+β2sin(β3k+β4))x(1)(k)，引入非线性时变正弦函数，通过4个参数的变化实现对系统行为总体趋势的模拟及预测；第二部分称作新信息项，为β5x(0)(k)，主要表现了最新信息对系统行为的影响；第三部分称作调整项，为β6k2+β7k+β8，对模型的模拟精确度进行进一步调整。同时，令 x(1)(1)=x(0)(1)+ε，利用参数ε修正x(1)(1)，以解决初始值信息丢失的问题。

3 基于粒子群算法的建模流程

鉴于模型的复杂性，本文利用粒子群算法计算模型的各个参数。

粒子群算法[9.10]（PSO）最早是由Eberhart和Kennedy于1995年提出，它的基本概念源于对鸟群觅食行为的研究。设想这样一个场景：一群鸟在随机搜寻食物，在这个区域里只有一块食物，所有的鸟都不知道食物在哪里，但是它们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢？最简单有效的就是搜寻目前离食物最近的鸟的周围区域。

PSO从这种模型中得到启示并用于解决优化问题。PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值（fitness value），每个粒子还有一个速度决定他们飞翔的方向和距离,然后粒子们就追随当前的最优粒子在解空间中搜索。

PSO初始化为一群随机粒子（随机解）。然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，这个解叫做个体极值pBest。另一个极值是整个种群目前找到的最优解，这个极值是全局极值gBest。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居，那么在所有邻居中的极值就是局部极值。其数学描述如下：

设搜索空间为D维，总粒子数为n。第i个粒子位置表示为向量Xi=(xi1，xi2，…，xiD)，第 i个粒子迄今为止搜索到的最优位置为Pi=(pi1，pi2，…，piD)，整个粒子群迄今为止搜索到的最优位置为 Pg=(pg1，pg2，…，pgD)，第i个粒子位置的变化率（速度）为向量Vi=(vi1，vi2，…，viD)。每个粒子的位置按如下公式进行变化：

其中，c1，c2为正常数，称为加速常数；rand()为[0,1]之间的随机数；ω为惯性权重。公式由三部分组成，第一部分是粒子先前的速度，说明了粒子目前的状态；第二部分是认知部分，表示粒子本身的思考；第三部分为社会部分。三个部分共同决定了粒子的空间搜索能力。第一部分起到了平衡全局和局部搜索的能力；第二部分使粒子有了足够强的全局搜索能力，避免局部极小；第三部分体现了粒子间的信息共享。在这三部分的共同作用下粒子才能有效地达到最好位置。

利用PSO计算NTDGM(1,1)模型中各个参数，以模拟值与原始值的总绝对百分误差为适应度函数：

综上所述，基于粒子群算法的非线性时变参数离散灰色预测模型的建模及求解过程可分为如下步骤：

（1）以(11)式作为适应度函数，利用PSO算法求解NTDGM(1,1)模型中各个参数，算法终止条件设置为最大迭代次数。

（2）将各个参数带入(9)式，计算 x̂(1)(k)的数值解，k=1，2，…，n。

（3）利用累减还原算子计算 x̂(0)(k)，k=2，3，…，n 。

4 算例分析

算例1：文献[11]研究提出了一种拓展的DGM(1,1)模型，但是并未考虑系统行为发展的非线性特点，利用其算例对比分析两种模型的模拟效果，NTDGM(1,1)1模型中各参数利用粒子群算法得到，令加速常数c1=c2=2，惯性权重ω设定为0.8，粒子数设定为60，迭代次数为600，并循环200次，得到各模型结果如下表所示。图1表示利用粒子群算法使适应度函数最小时，适应度函数值（总绝对百分误差）的收敛情况。

表1 与文献[11]对比各模型模拟预测值及平均绝对百分误差（%,MAPE）

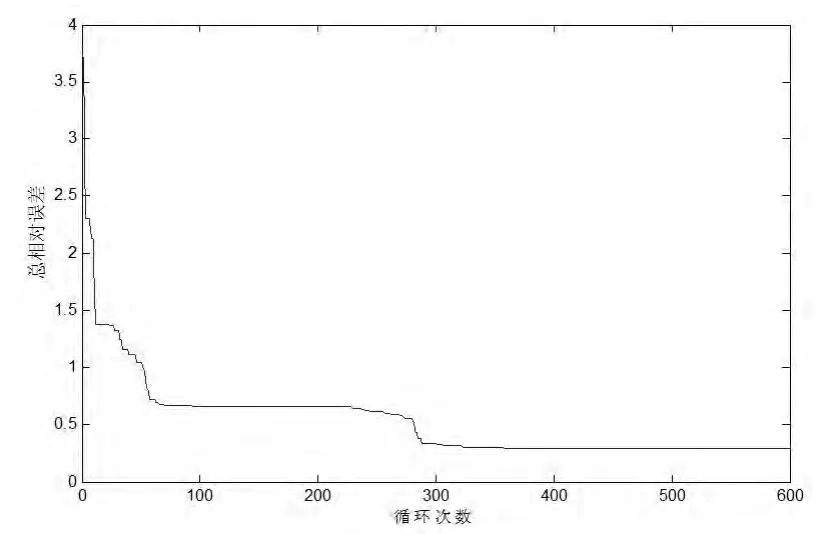
图1 适应度函数收敛情况

由表1可以看出，相对传统GM(1,1)模型和文献[11]提出的模型，本文提出的NTDGM(1,1)模型对13个数据的模拟预测值的平均绝对值相对误差仅为2.283%，大幅提高了精度。另外从图1中可以看出，大约在迭代360次左右时，适应度函数值（总绝对百分误差）逐渐收敛为0.2967（29.67%）。

算例2：文献[12]研究提出了一些特殊序列的改进的DGM(1,1)模型，并给出了几种模型的比较，本文以该文献所给出的算例进行验证。

利用粒子群算法计算本文所提出模型的参数，令加速常数c1=c2=2，由于数据趋势各不相同，为得到更精确地预测模型，本文将粒子数设定为100，迭代次数为600，并循环500次，惯性权重ω从0.4到1.2分别进行优化计算，得到各类型数据序列的模拟结果如表2所示。

由表2可以看出，相对于传统的DGM(1,1)模型以及文献[12]提出的DDGM(1,1)和IDGM(1,1)模型，本文提出的拓展非线性时变参数灰色离散预测模型的模拟精度极高，对各种类型趋势的数据均具有极好的模拟能力。对比算例1还以可看出，对于只有几个数据（算例2中每类数据序列只有5个数据）的序列进行模拟预测时，NTDGM(1,1)模型基本可以完全一致的模拟预测出原始数据序列。

5 结论

本文分析了传统的GM(1,1)及DGM(1,1)模型的模拟数据的增长率是一个定值，指出对非近似指数增长的数据序列，GM(1,1)与DGM(1,1)的模拟机预测效果较差。为解决实际工程中系统行随时间变化的复杂性，针对离散灰色模型参数恒定的缺陷，通过引入非线性时变项，并加入新信息构造了非线性时变参数离散灰色预测模型，鉴于模型的复杂性提出利用PSO算法求解模型参数，通过2个算例的对比分析可以看出NTDGM(1,1)模型很大程度上提高了模拟精度，特别是对“贫信息，少数据”的系统，几乎可以完全模拟各种类型趋势的数据序列。

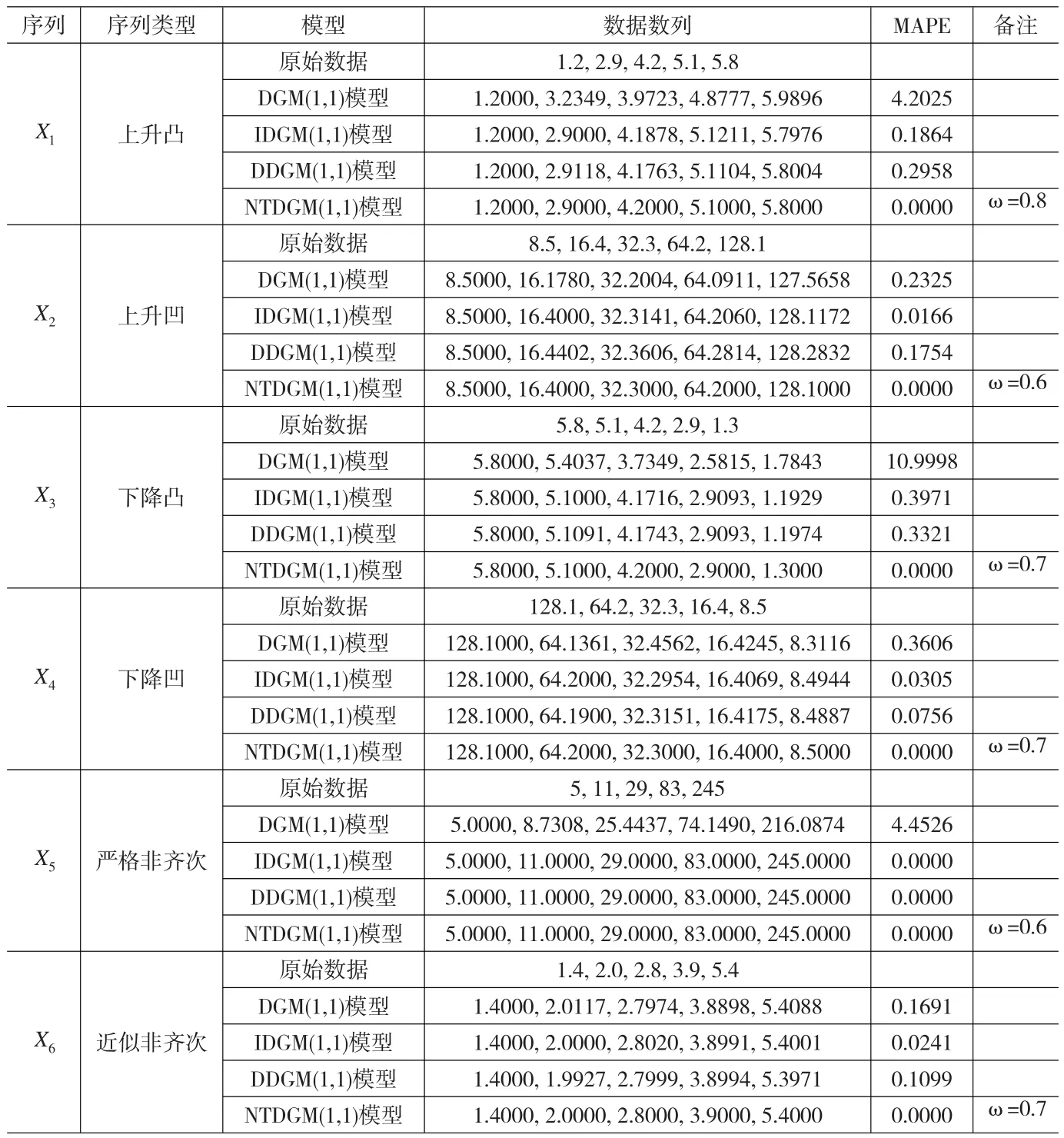
表2 与文献[12]对比各模型模拟预测值及平均绝对百分误差（%,MAPE）

[1]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2010.

[2]尚军亮,方敏.一种优化的高精度灰色GM(1,1)预测模型[J].电子与信息学报,2010,32(6).

[3]宋中民,同小军,肖新平.中心逼近式灰色GM(1,1)模型[J].系统工程理论与实践,2001,21(5).

[4]刘斌,刘思峰,翟振杰,等.GM(1,1)模型时间响应函数的优化[J].中国管理科学,2003,11(4).

[5]谢乃明,刘思峰.离散GM(1,1)模型与灰色预测模型建模机理[J].系统工程理论与实践,2005,25(1).

[6]姚天祥,刘思峰,党耀国.初始值优化的离散灰色预测模型[J].系统工程与电子技术,2009,31(10).

[7]刘卫锋,何霞,程少华,等.一类优化离散灰色模型及其等价模型[J].西华大学学报,2011,30(1).

[8]李伟,董伟栋,袁亚南.基于组合函数和遗传算法最优化离散灰色模型的电力负荷预测[J].电力自动化设备,2012,32(4).

[9]肖俊.基于粒子群算法的GM(1,1)模型及其应用[D].武汉:华中科技大学,2005.

[10]吴晓军,李峰,马悦,等.均匀搜索粒子群算法的收敛性分析[J].电子学报,2012,40(6).

[11]姚天祥,刘思峰.改进的离散灰色预测模型[J].系统工程,2007,25(9).

[12]曾波,孟伟.面向特殊序列的灰色预测建模方法[M].重庆:重庆大学出版社,2011.