KSS检验中漂移项与趋势项检验量分布研究

江海峰，庄 健，杨海文

(1.安徽工业大学商学院，安徽马鞍山243032；2.井冈山大学数理学院，江西吉安343009)

KSS检验中漂移项与趋势项检验量分布研究

江海峰1，庄 健1，杨海文2

(1.安徽工业大学商学院，安徽马鞍山243032；2.井冈山大学数理学院，江西吉安343009)

以数据生成是否含漂移项为依据，采用ADF检验模式分两种情况讨论非线性单位根KSS检验中漂移项、趋势项检验量分布。结果表明：在大样本下二者均收敛到维纳过程的泛函，为非标准分布。为在实证分析中使用这些检验量，通过蒙特卡罗模拟获得有限样本下常用临界值，模拟结果显示：虽然这些临界值随着样本的增加而上升或下降，但呈现稳定态势，且与理论分析结果相符。

单位根；KSS检验；蒙特卡洛模拟

自Phillips（1986）[1]首次从理论上证明不相关单位根变量之间会产生伪回归现象以来，单位根检验理论不断得到发展和完善，其中实证分析以DF类检验量最为常见。该类检验有3个明显特点：检验量分布不但取决于数据生成过程，也与检验模型设置形式相关；与单位根有关检验量分布只在大样本下成立，有限样本下分布并不存在；此类检验的原假设表示存在单位根，而备择假设表示序列为线性平稳过程。这3个特点表明其存在一定的缺陷，可从3个方面分别加以改进：针对第一个特点，王美今和林建浩（2012）[2]指出：应根据Enders（2004）[3]给出的严格检验步骤反复进行检验，即在检验单位根同时对数据生成过程进行检验，由此对检验模型中的漂移项和趋势项进行显著性检验。我国学者张晓峒等（2006）[4]、肖燕婷等（2008）[5]使用伪t检验考察了漂移项和趋势项的分布；为在有限样本下使用单位根检验量，可以通过Bootstrap方法替代临界值方法进行检验，如Ferretti&Romo等(1996)[6]、陶长琪和江海峰（2013，2014）[7-8]、江海峰等（2014）[9]的研究表明，使用Bootstrap方法可以提高检验效果；最后，针对第三个特点，可以将非线性平稳形式引入到单位根检验备择假设中，如使用门限自回归模型，其中Kapetanios等(2003)[10]讨论一阶指数平滑转换自回归（ESTAR）模型并提出了KSS检验，模拟结果显示，相对DF检验而言，这种模型具有更高的检验功效。此后许多研究者使用该方法进行了实证分析。在理论研究方面，蔡必卿等（2014）[11]采用PP检验模式重新考察KSS检验量分布，结果表明KSS检验量分布中含有未知参数，为在实证分析中使用该检验量，他们给出了非参数转换方法，转换后的检验量与Kapetanios等(2003)[10]检验量分布相同。然而，与传统单位根检验方法类似，KSS检验中也涉及到漂移项、趋势项选择，且数据生成与检验模型设置形式也对检验量分布产生影响。因此，为正确使用KSS检验，也必须对该类检验中的趋势项和漂移项进行显著性检验。鉴于目前尚没有文献对此进行讨论，本文按照数据生成是否含有漂移项分两种情况分别进行研究。

1 数据生成无漂移项检验模型

2 数据生成含漂移项检验模型

3 蒙特卡洛模拟

由于上述4种伪t检验量在大样本下都收敛到维纳过程的泛函，是非标准分布，为在实证分析中能够使用上述4种检验量，必须给出用于检验的临界值。下面使用蒙特卡洛模拟获得临界值。分别设定数据生成为式（1）和式（10），根据以上分析，由于4个检验量都不受ut-1的影响，为此取θ=0。设εt服从标准正态分布，样本容量分别为25，50，100，250，500和5 000，模拟次数为50 000次。根据式（14）可知，检验量t3与漂移项值c无关，因此当考察带漂移项的数据生成时，不失一般性假设c=1。模拟结果见表1，表2所示。显然，无论是漂移项检验量还是趋势项检验量，负临界值随着样本的增大呈现上升趋势，而正临界值呈现反向趋势。这表明同等置信水平下，检验量的区间估计变窄，说明随着样本的增大，估计的精度在提高，但变动趋势逐渐趋于稳定，这与它们在大样本下有理论分布相吻合。

4 实证研究

为说明如何使用上述检验量解决实际问题，结合实例进行分析。Nelson&Plosser(1982)[12]利用经典DF检验考察了美国14个宏观变量的平稳性，结果表明，除了失业率之外，其它13个序列都存在单位根。本文利用KSS检验并结合对漂移项、趋势项检验确定其是否平稳及其对应的数据生成形式。图1为失业率数据对数化后随时间变化的趋势，共有81个观测值。由图1可知，该序列基本在某个特定值左右上下波动，似乎呈现平稳态势，但不能确定是线性平稳还是非线性平稳形式。为此从一般的数据生成模型出发进行检验。首先假设数据生成中包括漂移项，在回归模型中包括趋势项，回归结果为

对应t检验量值分别为1.130，-0.446，-1.943，根据文献[10]得到KSS检验临界值在5%的显著性水平为-3.40，因此接受非线性项的系数为零的假设。由本文表2可知，趋势项的临界值约在正负2.9左右，显然趋势项t值落在的区域内，表明趋势项为零。剔除趋势项重新估计得

对应t检验量值分别为1.325，-1.909，而此种KSS检验量的临界值为-2.93，仍热表明非线性项为零，而根据表1的结果得到漂移项的临界值约在-2.80至2.50之间，显然1.325落入该区间内，表明漂移项也为零。最后剔除漂移项的估计结果为

对应t值为-1.370，而KSS检验临界值为-2.22，再次接受非线性项为零的假设。因此，利用KSS检验结合本文漂移项和趋势项检验表明对数化失业率数据为无漂移项单位根过程。

表1 不同样本容量下漂移项检验量t0，t1分位数Tab.1 Quantiles for drift statisticst0andt1under different sample size

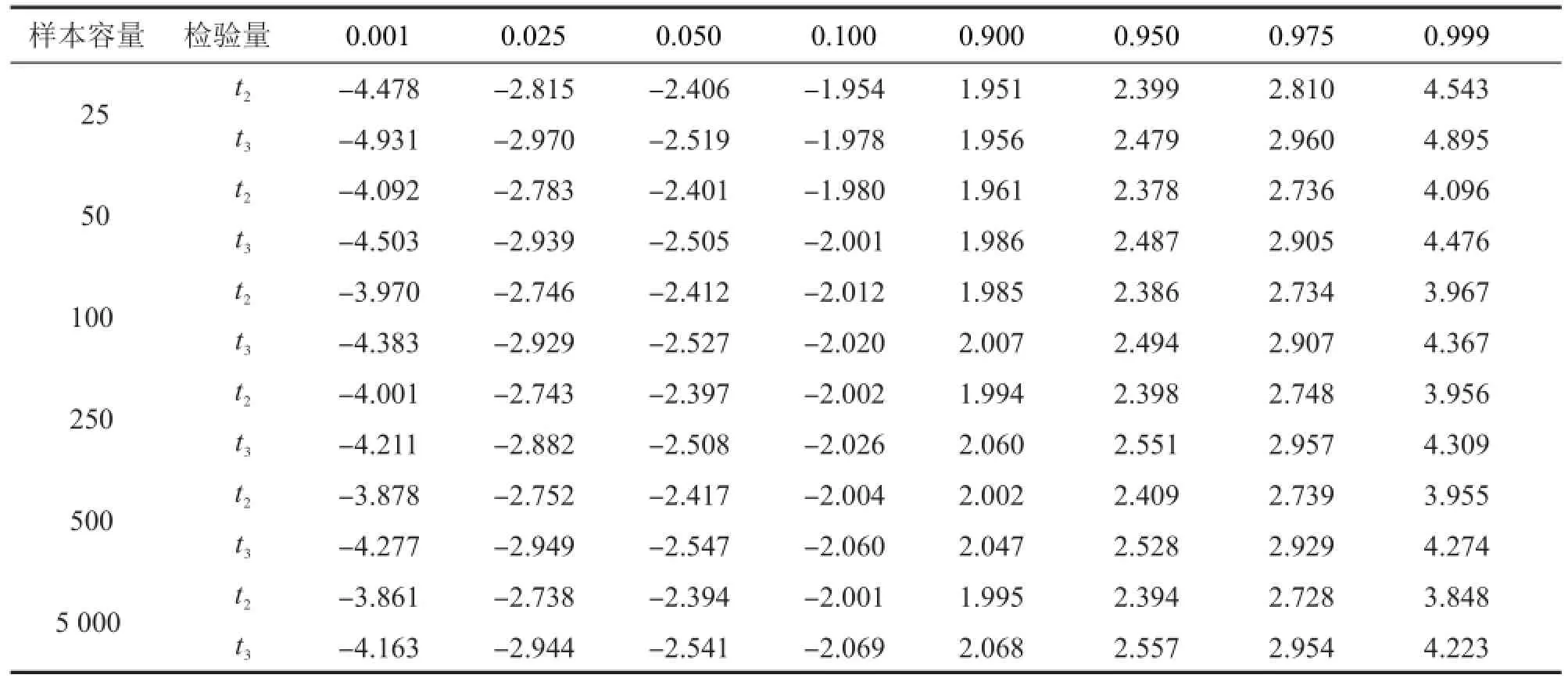
表2 不同样本容量下趋势项检验量t2、t3分位数Tab.2 Quantiles for trend statisticst2andt3under different sample size

5 结 论

（1）当数据生成不含漂移项的随机游走过程时，区分估计仅有漂移项、既有漂移项又有趋势项的KSS检验模型时，用于进行漂移项和趋势项检验的检验量t0，t1，t2具有明确的分布，且收敛到维纳过程的泛函；当数据生成含漂移项的过程时，估计有漂移项和趋势项的KSS检验模型时，用于检验趋势项的检验量t3也具有明确的分布，同时收敛到维纳过程的泛函。

（2）蒙特卡洛模拟结果表明：4种伪t检验量的临界值随着样本的变化呈现规律性；当样本足够大时，检验量的临界值呈现稳定态势，这与理论分析结果相一致。

（3）实证研究表明：通过在KSS检验中配合对漂移项、趋势项进行显著性检验，可以排除经典DF检验中可能掩盖的非线性平稳形式。

[1]Phillips P C B.Understanding spurious regressions in econometrics[J].Journal of Econometrics,1986,33(3):311-340.

[2]王美今，林建浩.计量经济学应用研究的可信性革命[J].经济研究，2012(2):120-132.

[3]Enders W.Applied Econometric Time Series[M].New York:John Willy&Sons Inc,2004:212-233.

[4]张晓峒，攸频.DF检验式中漂移项和趋势项的t统计量研究[J].数量经济技术经济研究，2006(2):126-135.

[5]肖燕婷，魏峰.单位根DF检验中漂移项、趋势项的分布特征[J].重庆工学院学报：自然科学，2008(7):139-144.

[6]Ferretti N,Romo J.Unit root bootstrap tests forAR(1)models[J].Biometrika,1996,83(4):849-860.

[7]陶长琪，江海峰.单位根过程联合检验的Bootstrap研究[J].统计研究，2013(4):106-112.

[8]陶长琪，江海峰.单位根检验中的Wald检验量研究：Bootstrap法VS临界值法[J].系统工程理论与实践，2014(5):1161-1170.

[9]江海峰，陶长琪，陈启明.ADF模式中漂移项和趋势项检验量分布与Bootstrap检验研究[J].统计与信息论坛，2014(6):3-10.

[10]Kapetanios G,Shin Y,Snell A.Testing for a unit root in the nonlinear STAR framework[J].Journal of Econometrics,2003, 112(2):35-379.

[11]蔡必卿，洪永淼.修正的KSS检验及其对中国通货膨胀率的应用[J].系统工程理论与实践，2014(2):313-322.

[12]Nelson C R,Plosser C.Trends and random walks in macroeconomic time series:Some evidence and implications[J].Journal of Monetary Economics,1982,10(2):39-162.

责任编辑：丁吉海

Research on Distribution for Drift and Trend Statistics Based on KSS Test

JIANG Haifeng1,ZHUANG Jian1,YANG Haiwen2
(1.School of Business,Anhui University of Technology,Ma′anshan 243032,China;2.School of Mathematics and Physics,Jinggangshan University,Ji′an 343009,China)

Based on whether the data generating process contains the drift or not,with ADF test mode,the distributions of the drift and trend statistics composed in nonlinear KSS unit root test were firstly deduced.The theoretic results show that these test statistics converge in distribution to the function of Wiener process,which manifests that these distributions are nonstandard.To apply these statistics to empirical research,the critical values were also obtained for finite samples with Monte Carlo Simulation.Simulation results demonstrate that although these values increase or decrease with the sample size increase,they are stable when the sample approaches to infinity and in accordance with the results of theoretical analysis.

unit root;KSS test;Monte Carlo simulation

F224.0

A

10.3969/j.issn.1671-7872.2015.01.017

2014-08-05

国家社会科学基金项目(13BJY011)

江海峰(1976-)，男，安徽巢湖人，博士，副教授，研究方向为数量经济理论及其应用。

1671-7872(2015)-01-0085-07