基于镜像延拓和窗函数的端点效应抑制方法
徐力彬,宋余庆,刘 毅
(江苏大学计算机科学与通信工程学院,江苏镇江212013)
1 概述
Hilbert-Huang变换(Hilbert-Huang Transform,HHT)是由Huang N E等人通过深入分析和总结后提出的一种新的非平稳非线性信号分析方法[1]。该方法主要包含2个部分:经验模态分解(Empirical Mode Decomposition,EMD)和 Hilbert谱 分 析(Hilbert Spectral Analysis,HAS),其中 EMD 为核心部分[2]。与传统方法相比,EMD无须预先设定任何基函数,而是根据信号特点自适应地将原始信号分解为一系列固有模态函数(Intrinsic Mode Function,IMF),去除了快速傅里叶变换方法中引入的谐波基函数,也没有小波分析复杂信号过程中产生信号模糊与失真的问题[3-6]。然而,HHT变换也有一定的局限性,例如端点效应问题[7]和模态混叠问题[8]等。尤其是端点效应问题会严重妨碍信号的特征提取,从而导致信号分析的误差。
EMD中使用三次样条函数对包络进行拟合时,由于难以确定端点处是否为极值点,导致出现了端点效应问题。国内外专家针对端点效应已经提出了多种有效的抑制方法,包括镜像延拓[9]、极值延拓[10]、基于神经网络预测的数据延拓法[11]以及多项式拟合延拓法[12]等。这些方法在抑制端点效应方面都有着良好的效果,但同时也存在弊端,如多种延拓方法存在同一种缺陷,即在对原始信号进行延拓处理以后,其端点依然是不固定的,拟合的上下包络线两端还是会出现发散现象,只是在EMD完成后截去延拓部分,端点效应相对减轻。本文在镜像延拓的基础上,利用余弦窗函数法对延拓后的信号进行处理,使样条函数可以更好地拟合包络线,对端点效应起到抑制作用。
2 EMD算法
2.1 算法简介
EMD算法是HHT的核心算法之一,用来将一个信号的能量按照时域各种固有尺度的波动进行分解,得到一系列频率从小到大的IMF。这里IMF须满足如下2个性质[13]:
(1)信号的极值点数目和过零点数目相等或最多相差一个;
(2)由局部极大值构成的上包络线和由局部极小值构成的下包络线的平均值为0。
EMD的分解过程如下:
Step1设原始信号曲线为X(t),求出所有的极大值、极小值。
Step2对极值使用三次样条函数进行处理,描绘出原始信号的上、下包络线,分别记为 u(t)和v(t)。
Step3将上、下包络线的平均值记为:
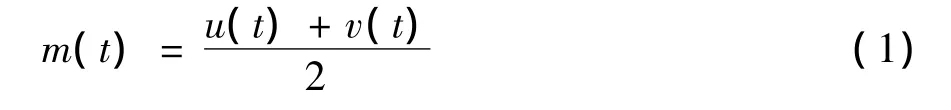
Step4将均值曲线m(t)从原信号X(t)中分离出来,得到的剩余部分记为:

Step5判断h1(t)是否满足IMF的2个性质。若满足,则h1(t)为第一个IMF分量;否则,记h1(t)为X(t),重复Step1~Step4,直到第k次迭代之后得到一个IMF,将其记为c1(t)=h1k(t)。这里,将标准差准则作为第k次迭代的终止原则,使其位于0.2~0.3 之间,停止筛选[14]。
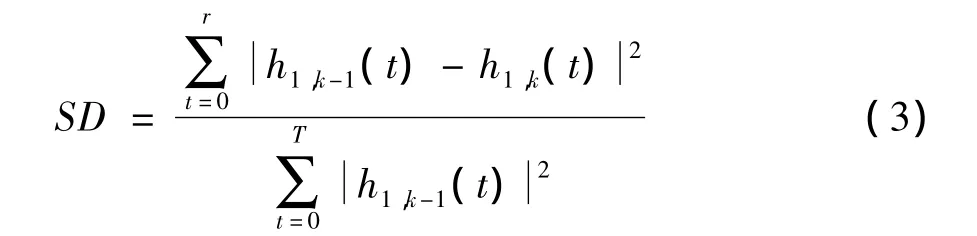
Step6记r1(t)=X(t)-c1(t)为新的待处理信号,再重复Step1~Step5,得到第2个IMF分量,将其记为c2(t)。继续重复Step1~Step6,当所得余项rn(t)是一个单调信号或者rn(t)的值小于事先给定的阈值时,分解结束[15]。
综上所述,原始信号X(t)为所有IMF分量与余项rn(t)的和:
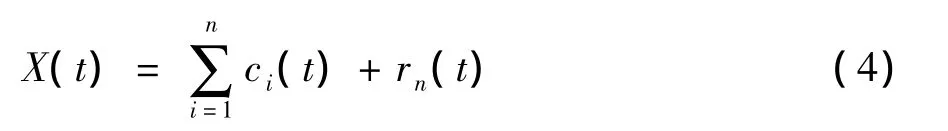
2.2 端点效应
在EMD中,为得到信号的瞬时平均包络线,需要对原信号的局部极大值和极小值分别进行三次样条插值算法拟合出上、下包络线后,再计算出信号的局部平均值。由于信号两端无法同时处于极大值和极小值点,因此上、下包络线在数据信号两端不可避免地会出现偏移,并且这种偏移现象会随EMD的进行逐渐传播到信号内部,从而严重影响信号分解的质量[16],这种现象就是端点效应,如图1所示,其中,实心点为延拓后的点,实线为真实的包络线,虚线为无端点约束产生的错误包络线。

图1 端点效应示意图
2.3 抑制端点效应的常用方法
2.3.1 常用延拓方法
延长数据序列或者在数据两端增加极值点来抑制端点效应是得到普遍认可的一种方法[17]。对于复杂的信号,准确地对数据序列进行延拓是不现实的,但可以使延拓后得到的平均包络线与真实平均包络线相对较为接近,这是到目前为止普遍认为的抑制端点效应的有效途径。常用的延拓方法如下:
(1)镜像延拓法
镜像延拓法的实质是将原始信号对称地延拓成一个闭合的环形信号,这种环形信号没有端点,其上、下包络线完全由信号内部确定,从而在根本上避免了端点效应的产生。但是,当无法确定端点是否为极值点时,可能会使延拓部分和原始信号的均值有明显差异,从而影响EMD产生的最终结果。
(2)极值延拓法
极值延拓法不需要对信号本身延拓,可以只对信号的极值进行延拓。该方法在镜像延拓的基础上,对延拓后的对称点是否为极值点进行了判断,提高了处理效果[18]。但该方法也存在缺陷,即若将端点都作为极值点进行处理,端点处的包络线会产生收缩,从而导致包络线失真。
(3)多项式拟合延拓法
通过多项式拟合法算出信号端点处对应的函数值,将其作为端点处极值的近似值。用正交多项式拟合的方法会比一般的多项式拟合更加准确,算法复杂度也不搞。该方法对准周期信号延拓效果比较好,但对随机信号等变化规律不明显的信号在端点效应抑制方面的效果一般。
2.3.2 窗函数法
窗函数法是一种能够有效抑制端点效应的方法,对信号进行窗函数处理可以增强函数中心处的信号,同时抑制远离中心处的信号[19]。在EDM 分解过程中,端点效应从端点逐渐向信号内部发散,误差不断积累,导致发散程度越来越严重。
在对信号进行窗函数处理后,信号端点处的值变为0,包络线也会相对平滑。因此,三次样条函数能够更真实地拟合包络线,最终上、下包络线收逐渐收敛于端点,不再发散。
在窗函数的选取问题上,笔者不需要自己设计窗函数,国内外数学家已经提出了很多能适合不同需要的窗函数。在处理端点效应的问题上,应用较多的有汉宁窗、海明窗、矩形窗和余弦窗等。
3 本文算法
当原信号进行窗函数处理后,原信号的包络线将被改变,可能会对接下来的过程带来误差,这时可以考虑先将信号进行延拓处理,再进行加窗,最后在EMD过程结束后舍去延拓部分。
仿真信号表达式如下:
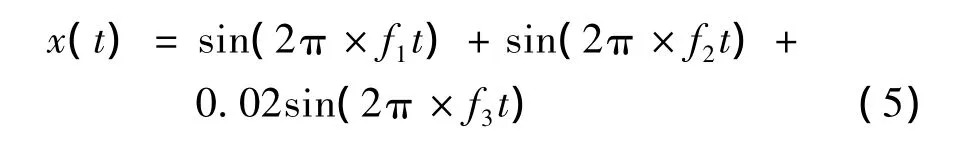
其中,f1=200 Hz;f2=100 Hz;f3=50 Hz。采样频率为1 000 Hz。信号由3个正弦信号组成。图2为原信号x(t)分解出来的3阶IMF,分解时没有对原始信号进行任何处理,可见IMF1,IMF2,IMF3都产生了明显的端点效应,而且随着分解过程的进行,端点的发散程度越来越严重,在IMF3中甚至已经无法表达出原信号中的低频部分。
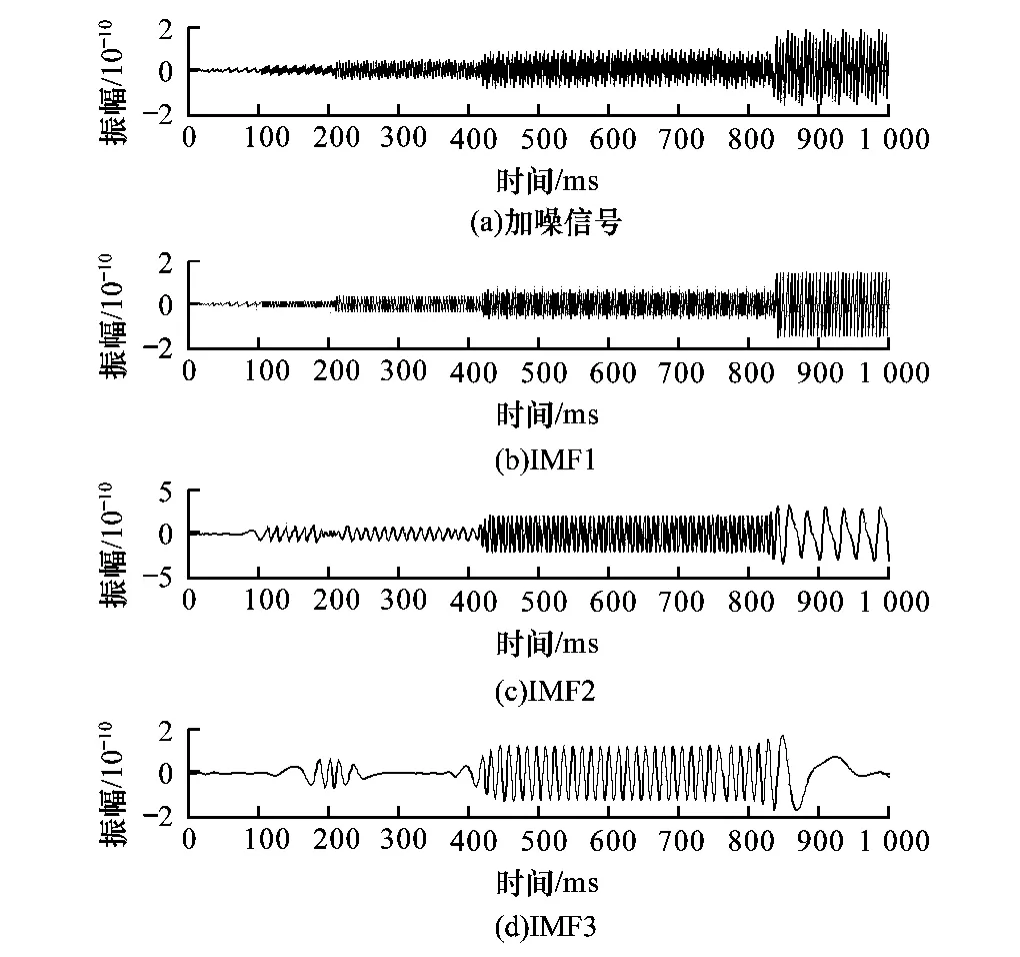
图2 未经处理的EMD分解结果
本文方法的具体步骤如下:
(1)将原信号x(t)进行镜像延拓处理,得到延拓后的信号y(t)。
(2)将延拓后的信号y(t)用一定周期ΔT的余弦窗函数α(t)进行处理。即将y(t)与α(t)进行内积运算,得到信号 σ(t)=[x(t),α(t)],确定处理信号σ(t)的所有极值点。
(3)计算由局部极大值和极小值点确定的上下包络线Mmax(t)和Mmin(t)。
(4)计算包络线均值:
m(t)=(Mmax(t)+Mmin(t))/2
(5)求出h(t)=y(t)-m(t)。
(6)如果h(t)不满足IMF的条件,则重复以上循环;如果h(t)是一个IMF,将信号y1(t)=y(t)-h(t)作为原始信号重复以上循环。当yk(t)成为一个单调信号时,循环结束。
4 仿真实验及结果分析
4.1 实验分析
4.1.1 延拓处理
采用余弦窗函数对原始信号进行处理后,有可能会改变信号的特征,因此,改进算法先对信号进行镜像延拓,使延拓信号和原始信号的交界处变得光滑。
本文将仿真信号x(t)作为延拓对象,在从左向右的第L个极值点处和从右向左的第R个极值点处分别设置2个光滑的反射面,将信号向外反射,得到数据序列长度两倍于反射信号长度的周期性信号。这时,信号作为一个环形的闭合曲线,满足了原信号曲线在端点处一阶、二阶倒数存在的要求。然后将闭合曲线作为一个整体进行EMD分解,最终取上半部分作为分解结果。图3所示结果为延拓后的信号,可以看出,此时信号两端点处已呈一定的周期性。

图3 镜像延拓后的EMD分解结果
4.1.2 加窗处理
余弦窗是信号处理中应用较为广泛的一种窗函数,在本文中,余弦窗函数可被定义为:
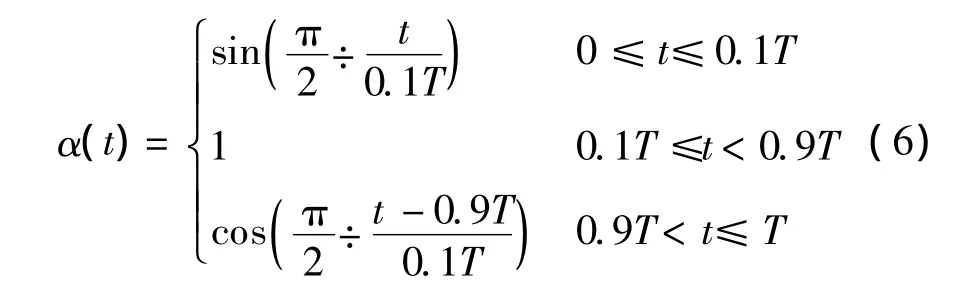
式(6)的曲线图如图4所示,可见,在窗函数中间部分的值为1,窗函数两端的值逐渐减少至0。这样,信号端点处的值变为0,包络线变得相对平滑,拟合出的包络线也变得更为真实。随着EMD分解的进行,上下包络线逐渐收敛于端点,发散现象就不会再发生。图5为延拓后信号进行余弦窗函数处理后的情况,可见IMF1,IMF2,IMF3的端点效应均得到了明显的抑制,而且IMF4分量中的低频部分仍能表达出来。
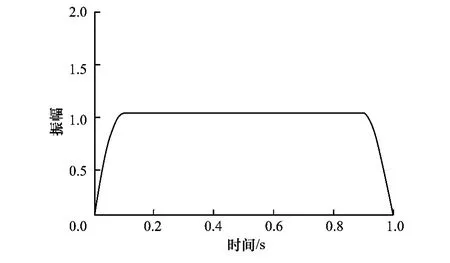
图4 余弦窗函数α(t)

图5 加窗处理后的EMD分解结果
4.2 评价指标
目前,所有提出的端点效应抑制方法都需要一个定性与定量相结合的评价指标来综合考虑方法的优劣。本文主要采用均方根有效值评价法来定性分析端点效应抑制方法的效果:可以先计算出原始信号和通过筛选得到的各个IMF分量的均方根有效值。如式(7)所示。
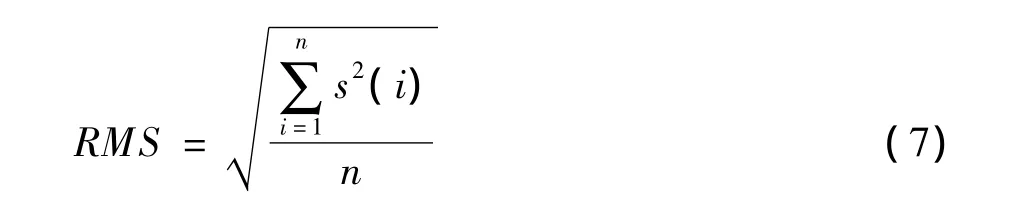
其中,RMS表示信号有效值;s(i)为信号序列;n为信号的采样点数。
按式(7)比较各IMF分量有效值的总和与原信号有效值,得到一个评价指标θ。

其中,RMSoriginal表示原始信号的有效值;RMSi表示第i个IMF分量的有效值;n为IMF分量的个数,其中包括EMD的残留项。
根据定义,θ≥0,当端点效应对EMD分解过程没有影响时,θ=0。θ值越大,说明端点效应对EMD分解的影响越大。θ值越小,表明IMF分量的发散程度越小,端点效应的影响也就越小。
4.3 实验结果
实验给出了未加任何处理的EMD算法、极值对称延拓法、镜像延拓法、窗函数法和改进算法对处理端点效应的效果评价,给出了EMD分解前后的效果对比参数值 θ。从表1中可以看出,未加处理的EMD算法的θ值明显偏大,极值对称延拓法、镜像延拓法、窗函数法的θ值都有不同程度的减小,而本文改进算法的θ值较其他4种算法都小,说明对端点效应的抑制效果更好。

表1 多种算法的端点效应抑制评价结果
5 结束语
本文提出了一种将镜像延拓和余弦窗函数结合的端点效应抑制方法。首先将原信号进行镜像延拓处理,然后在对延拓后信号进行IMF提取之前,在其两端加上余弦窗函数,使得上下包络线能够更好地拟合。该方法弥补了镜像延拓可能使延拓部分信号与原始信号的均值有明显差异的不足,同时也解决了单纯窗函数法因为改变原信号而可能带来其他问题的缺陷。另外,本文利用θ值作为评价指标综合评价了多种抑制算法的效果,结果显示出改进方法较传统方法略有提升。但是,在EMD分解过程中,由于每次筛选得出的新信号发散程度不同,如果使用单一窗函数对筛选后的新信号进行处理可能还会带来信号失真等问题,随着EMD的进行,这种信号失真现象可能越来越严重。因此,对于EMD分解中的端点效应问题还有待进一步研究。
[1] Huang N E,Shen Zheng,Long S R,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[J].Proceedings ofRoyalSociety London,1998,454:903-995.
[2] 王黎黎.基于希尔伯特-黄变换的时频分析算法研究[D].西安:西安电子科技大学,2009.
[3] 秦 毅,秦树人,毛永芳.改进的Hilbert-Huang变换在信号瞬态特征提取中的应用[J].冲击与振动,2008,27(11):129-130.
[4] Guo D,Peng Z P.Vibration Analysis of a Cracked Rotor Using Hilbert-Huang Transform[J].Mechanical Systems and Signal Processing,2007,21(8):3030-3041.
[5] Li X L,Bassiunya A M.Flute Breakage Detection During End Milling Using Hilbert-Huang Transform and Smoothed Nonlinear Energy Operator[J].International Journal ofMachine Toolsand Manufacture,2007,47(6):1011-1020.
[6] Feldman M.Considering High Harmonics for Identification of Non-linear System by Hilbert Transform[J].MechanicalSystems and SignalProcessing,2007,21(2):943-958.
[7] Yan Ruqiang,Gao R X.A Tour of the Hilbert-Huang Transform:An Empirical Tool for Signal Analysis[J].IEEE Instrumentation & Measurement Magazine,2007,10(5):40-45.
[8] 张 超,陈建军.EEMD方法和EMD方法抗模态混叠对比研究[J].振动与冲击,2010,29(8):87-90.
[9] 苏玉香,刘志刚,李科亮,等.一种改善EMD端点效应的新方法及其在谐波分析中的应用[J].电工电能新技术,2008,27(2):33-36.
[10] Zhao Jinping,Huang Daji.Mirror Extending and Circular Spline Function for Empirical Mode Decomposition Method[J].Journal of Zhejiang University,2001,2(3):247-252.
[11] 顾小丽,李培良,谭海涛,等.基于 RBF神经网络的EMD方法在海平面分析中的应用[J].海洋与湖沼,2009,40(5):532-534.
[12] 朱金龙,邱晓晖.正交多项式拟合在EMD算法端点问题中的应用[J].计算机工程与应用,2006,42(23):72-74.
[13] 甘锡林,黄韦艮,杨劲松,等.基于希尔伯特-黄变换的合成孔径雷达内波参数提取新方法[J].遥感学报,2007,11(1):39-40.
[14] 张 博.基于Hilbert-Huang变换的滚动轴承故障诊断方法研究[D].西安:西安理工大学,2009.
[15] 戴桂平.基于EMD的时频分析方法研究[D].秦皇岛:燕山大学,2005.
[16] Zeng Kan,HeMingxia.A SimpleBoundaryProcess Technique for Empirical Decomposition[C]//Proceedings of International Geoscience and Remote Sensing Symposium,September 20-24,2004,Anchorage,USA.Washington D.C.,USA:IEEE Press,2004:4258-4261.
[17] 许宝杰,张建民,徐小力,等.抑制EMD端点效应方法的研究[J].北京理工大学学报,2006,26(3):196-200.
[18] 黄大吉,赵进平,苏纪兰.希尔波特-黄变换的端点延拓[J].海洋学报,2003,25(1):1-9.
[19] 任达千,吴昭同,严拱标.EMD端点效应的评价指标及抑制端点效应的窗函数法[J].制造业自动化,2007,29(1):21-24.

