粗糙集代数与BCK代数

刘春辉

（赤峰学院 教务处，内蒙古 赤峰 024000）

0 引言

粗糙集理论是由波兰数学家Pawlak于1982年首次提出的[1]，经过二十几年的研究与探索，在理论与应用上都取得了令人瞩目的成果，尤其是由于20世纪80年代末和90年代初该理论在知识发现等领域的成功应用而受到国际数学界和计算机界的广泛关注[2].非经典数理逻辑代数及其相关逻辑系统是人工智能领域的重要研究分支之一，众多的学者基于不同的角度提出了各种不同形式的非经典数理逻辑代数，如MV代数、BL代数、R0代数、格蕴涵代数和BCK代数等，对相关逻辑系统的研究也有较为成熟的研究工作[3-6].如果能够建立非经典数理逻辑代数与粗糙集代数的联系，就可以借助非经典数理逻辑的研究结果讨论粗糙集逻辑.目前，这方面的探索也获得了很多研究成果[7,8].以此为基础，本文探讨将粗糙集代数构造为BCK代数的方法，其中粗糙集采用上、下算子的表示形式,证明了在适当选取◇运算后，粗糙集代数就可成为BCK代数的结论.

1 BCK代数及粗糙集的基本概念

定义1.1[1]设U是一个非空有限集合，称为论域，如果R为U上的一个等价关系，则称二元组（U，R）是一个Pawlak近似空间.坌X哿U，定义X关于Pawlak近似空间(U,R)的下近似R(X)和上近似(X)分别为：

其中[x]R={y∈U|（x,y）∈R}是x关于R的等价类，U/R={[x]R|x∈U}是所有R等价类的集合.对于X哿U，称为R-粗糙集.若，则称为R-精确集.否则称为R-近似集.

定义1.2[6]称(2.0)型代数(B,*,0)为BCK代数，如果坌x,y,z∈B满足：

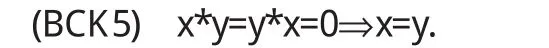
关于BCK代数的其它方面的结构性质，请参见文献[6].

2 粗糙集代数与BCK代数

设(U,R)是一个Pawlak近似空间，且

为R-粗糙集全体之集.

引理2.1[2]设X,Y哿U为R可定义集，即为若干R等价类之并集，则(X,Y)∈N(A)当且仅当X哿Y且(Y-X)∩S=覫，其中集合S={x∈U||[x]R|=1}.

对坌(X1,Y1),(X2,Y2)∈N(A)，令

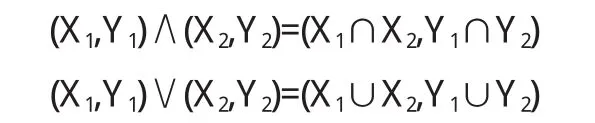
容易验证∧和∨是N(A)上封闭的二元运算且(N(A),∧,∨)构成有界格.其中序关系为：

(U,U)和(覫,覫)分别为格中最大元与最小元.故(X1,Y1)=(X2,Y2)圳X1=X2且 Y1=Y2.

现在，我们在N(A)上定义二元运算◇使得坌(X1,X2),(Y1,Y2)∈N(A)，

其中，坌X哿U，Xc=U-X.

引理2.2 N(A)对二元运算◇是封闭的.

证明 设坌(X1,X2),(Y1,Y2)∈N(A)，则由引理 1知X1哿X2，(X2-X1)∩S=覫 且 Y1哿Y2，(Y2-Y1)∩S=覫，从而 X2c哿X1c且Y2c哿Y1c，故 X1∩Y2c哿(X1∪Y2c)∩Y1c∩X2)且

故 (((X1∪Y2c)∩Y1c∩X2)-(X1∩Y2c))∩S=覫.因此(X1,X2)◇(Y1,Y2)∈N(A).

定理 2.1(N(A),◇,(覫,覫))构成 BCK代数.

证明 坌(X1,X2),(Y1,Y2),(Z1,Z2)∈N(A),分如下八步完成证明：

(1)证明等式((X1,X2)◇(Y1,Y2))◇(Z1,Z2)=((X1,X2)◇(Z1,Z2))◇(Y1,Y2).事实上，因为

所以比较便可得((X1,X2)◇(Y1,Y2))◇(Z1,Z2)=((X1,X2)◇(Z1,Z2))◇(Y1,Y2).

(2)证明等式(X1,X2)◇((X1,X2))◇(Y1,Y2))=(Y1,Y2)◇((Y1,Y2))◇(X1,X2).事实上，因为

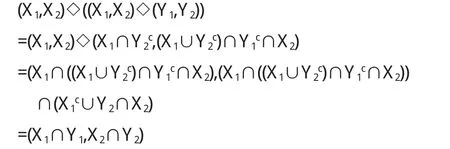
类似的方法可证(X1,X2)◇((X1,X2)◇(Y1,Y2))=(X1∩Y1,X2∩Y2)，因此

(3)证明等式(X1,X2)◇(X1,X2)=(覫,覫)，即 BCK3成立.事实上

(4)证明等式(覫,覫)◇(X1,X2)=(覫,覫)，即 BCK4成立.事实上

(5)证明等式(((X1,X2)◇(Y1,Y2))◇((X1,X2)◇(Z1,Z2)))◇((Z1,Z2)◇(Y1,Y2))=(覫,覫),即证明 BCK1成立.事实上，由(1)-(4)得

(6)证明等式((X1,X2)◇((X1,X2)◇(Y1,Y2)))◇(Y1,Y2)=(覫,覫)，即证明 BCK2成立.事实上，由(1)和(3)得

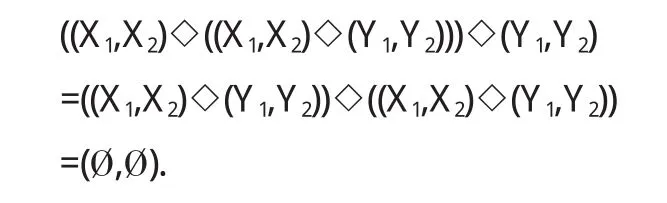
(7)证明等式(X1,X2)◇(覫,覫)=(X1,X2)，事实上

(8)证明 BCK5，即假设(X1,X2)◇(Y1,Y2)=(Y1,Y2)◇(X1,X2)=(覫,覫)，往证(X1,X2)=(Y1,Y2).事实上，由(2)和(7)及假设条件得

综合(1)-(8)得(N(A),◇,(覫,覫)为 BCK代数.

3 结论

本文在深入分析粗糙集代数与BCK代数之间关系的基础上，给出了一种由粗糙集代数构造BCK代数的方法，证明了在选取适当的◇运算后，粗糙集代数就成为BCK代数的结论.这一结论为借助于BCK代数及BCK逻辑研究粗糙集逻辑提供了必要的理论基础.此外，我们也可以借鉴本文的研究方法去讨论其它逻辑代数结构与粗糙集代数间的相关问题，这将是今后研究的主要方向.

〔1〕Paw lak Z.Rough sets[J].International Journal of Computer and Information Science,1982,11:341-356.

〔2〕张文修,吴伟志,梁吉业,李德玉.粗糙集理论与方法[M].北京:科学出版社,2001.

〔3〕王国俊.MV代数、BL代数、R 0代数与多值逻辑[J].模糊系统与数学,2002,16(2):1-12.

〔4〕Xu Yang,Jun Y B,Qin Keyun,Liu Jun.Lattice Logic[M].Berlin:Springer,2004.

〔5〕刘春辉.正则剩余格的生成⊙与素⊙理想[J].四川师范大学学报(自然科学版),2010,33(5):621-625.

〔6〕Huang Yisheng.BCI-algebras[M].Beijing:Science Press,2006.

〔7〕秦克云,涂文彪.粗糙集代数与格蕴涵代数[J].西南交通大学学报,2004,39(6):754-757.

〔8〕乔全喜,秦克云.粗糙集代数与BL代数[J].计算机工程与应用,2008,44(33):46-47.

〔9〕岳织锋，韩海山，赵桐.线性互补问题罚函数法的收敛性[J].内蒙古民族大学学报(自然科学版)，2013,28（6）：631～634.