灰色聚类决策中指标权重和综合决策测度权系数的确定

强凤娇

（陕西科技大学 管理学院，西安 710021)

0 引言

在灰色聚类评价与决策的理论研究中，指标权重确定问题一直是学者们关注并进行研究的重要问题之一。邓聚龙教授在1987年提出灰色聚类评估方法时便提出了一种基于白化权函数临界值的灰色变权聚类权重确定方法[1]，刘思峰教授提出了灰色定权聚类评估方法[2]，王正新等提出灰色聚类评价中分类权重与重要性权重的不同，并以分类权重进行方案评价[3]，彭安华提出在灰色聚类评价中将指标的灰色聚类权与重要性权重进行组合[4]。目前关于灰色聚类决策的指标权重确定问题，已经取得了不少成果，其确定方法也达数十种之多，但仍存在需要改进的地方。另外在灰色聚类决策中，广大学者均将关注点放在指标权重的确定上，而对灰类综合决策测度的权重确定问题研究，目前文献研究中还较少。本文将针对灰色聚类决策中的指标权重确定及灰类综合决策测度的权重确定两个方面的问题进行分析并改进，力求使灰色聚类决策的权重确定问题更加合理。

1 基于组合权重思想的灰色聚类决策指标权重的确定

1.1 目前灰色聚类决策中指标权重的确定与不足

目前常见的应用于灰色聚类决策中的指标权重可以采用三种标准进行分类，按确定的权重是否存在人为因素的影响可分为为主观权重和客观权重，按确定的权重是否考虑实际评价问题的评价目的与要求可分为重要性权重和分类性权重，按确定的指标权重值是否适用于所有评价方案可分为固定（公共）权重和可变权重。

主观权重由评价专家采用层次分析法、Delphi法、古林法等来确定，虽比较贴近实际要求，但不能客观科学地体现评价方案的数据信息且受人为因素影响较大，经常会夸大或缩小某些指标的作用；客观权重是根据决策方案中的指标数值信息采用熵权法、离差最大化法、主成分分析法等来确定，注重各个指标数值的相对差异大小，并仅仅依据指标数值间相对差异大小来确定指标权重，没有考虑方案的评价目的，忽视了评价目的对各个指标的相对重要性要求，经常脱离实际。

重要性权重反映在不同的评价目的要求下，各个指标在整个评价指标体系中受重视程度的不同，与各具体方案（评价对象）的各个指标具体取值无关，可以由主观或客观赋权法来确定，属于固定权重，但大多由主观赋权法确定，且确定的重要性权重与主观权重存在较强的对应关系；分类性权重关注的是不同方案各个评价指标的离散度，通过指标数值的相对差异大小尽可能较大程度的将待评价方案区分开来，其确定的指标权重完全由各具体方案的各个指标取值决定，其确定的权重既可能为固定权重也可能为可变权重，一般情况下由客观赋权法确定，且确定的分类性权重与客观权重存在较强的对应关系。

固定权重是在考虑评价总目的要求或不同方案提供的相关性数据信息的基础上，计算得到对所有评价方案均适用的相同指标权重，但没有考虑特定评价方案提供的特有信息，强调共性忽视个性，其与重要性权重存在较强的对应关系，但也有一部分固定权重属于分类权重；可变权重是利用一些客观赋权法的思想及特定方案提供的各指标数值计算得到该方案的特有权重系数，对不同评价方案采用不同的指标权重，但没有考虑评价的目的要求及与其他方案的相关性数据信息，强调个性忽视共性，其应属于分类权重的一部分。

以上指标权重分类标准各自形成的两个分类虽然在含义与作用上存在差异，但其仍具有较明显的对应关系，任何一个分类标准中形成的两类权重均各有利弊，其考虑问题的出发点与侧重点也各有不同，但任一分类中的两类权重在实际评价问题中并不对立，单独采用往往不能很好的解决实际评价问题，如果能综合各自分类中两类权重的优点，把主观与客观权重有机结合、重要性权重和分类性权重有机结合，固定权重与可变权重有机结合，一定会使灰色聚类决策评价指标的权重确定更加公平合理。

1.2 基于组合思想的灰色聚类决策指标权重确定

通过上述分析发现，在灰色聚类决策中将主观权重和客观权重进行组合，既避免了主观权重人为因素影响大的问题又避免客观权重过分依赖指标取值而脱离专家经验与知识判断的弊端；将重要性权重和分类性权重进行组合，可以同时兼顾反映评价目的指标重要性程度要求和待评价方案各个指标数值间的相对差异大小；将固定权重和可变权重进行组合，可以在一定程度上满足评价的共性要求并兼顾特定方案的特殊性需要。在实际评价中，以上任一形式的组合权重均可以形成一定程度的互补，比单纯采用某一类权重得到的评价效果更加客观和全面。关于组合权重的计算，在乘法合成归一化组合方法[5]设计的基础上，为降低其组合可能导致大者更大、小者更小的倍增效应，并灵活反映实际评价问题中评价主体的需要，本文设计了式（1）所示的指数乘法合成归一化组合的方法。

式（1）中，α称为主观权重系数（或重要性权重系数、固定权重系数），且0≤α≤1，α的具体取值由评价中对专家意见（或评价目的与要求、共性要求）的重视程度来决定，如果评价中相对更重视专家意见，就应给予α较大的值，反之亦反；wj1表示指标j的主观权重（或重要性权重、固定权重）；w2jwij2表示方案i的指标j的客观权重（或分类性权重、可变权重）；wij表示方案i的指标j的组合权重。

本文利用层次分析法确定指标的重要性权重，利用信息熵确定指标的分类性权重，并利用式（1）将两者进行组合作为灰色聚类决策指标的组合权重，该组合权重体现的是重要性权重与分类性权重的组合，实际上也同时体现了主观权重与客观权重的组合，固定权重与可变权重的组合。

1.3 基于层次分析法的灰色聚类决策指标重要性权重确定

层次分析法（Analytic Hierachy Process，AHP）自T.L.Saaty教授提出以来，以其层次化、体系化、简洁化的优点，将定性分析与定量计算有机结合，近年来在众多领域作为一种多指标评价的决策方法或指标权重确定方法，得到了广泛应用。

AHP法把复杂问题分解成若干要素（指标），并按要素间的支配关系形成递阶层次结构，通过两两比较的方式确定层次中诸要素的相对重要性，即诸要素的重要性权重。

1.4 基于信息熵的灰色聚类决策指标分类权重确定

信息熵是对系统不确定程度的量度，熵越大就表示系统的不确定程度越大。王正新[3]提出应用信息熵确定灰色聚类决策的分类权重，但认为在灰色聚类决策评价中，对特定评价方案进行分类真正有意义的是其自身指标数据提供的分类权重，与其他方案的指标取值及反映评价目的要求的重要性权重无关，该认识是不全面的，而且依此形成的分类有可能不符合实际情况。在灰色聚类决策中，对某一具体指标而言，信息熵越大意味着信息的模糊性越大，提供用于分类的有用信息越少，故应给予该指标较小的分类权重，反之亦反，从而体现精确胜于模糊的权重确定原则。

灰色聚类决策中白化权函数的确定，一般是根据实际问题的背景从参与聚类对象角度或所有同类对象的整个大环境角度，由评价专家依据经验主观拟定，因此对不同分指标j（j=1,2,…,m）计算所得各灰类的分指标聚类系数（白化权函数值）(xij)之和并不一定相等，各指标的聚类系数之间不存在可比性，不能直接利用其来区分不同分指标对评价方案所属类别的贡献大小，为此首先需要利用式（2）求出归一化分指标聚类系数(xij)，显然归一化后的分指标聚类系数和相等且等于1，各分指标具备了可比性。

对评价方案i的指标j的归一化聚类系数，当各分量均相等，即等于1/s时，得到最大分类信息熵Eij=1，表明指标j对于方案分类不起任何作用，完全可以删除掉；当其中一个分量等于1，其余分量均为0时，得到最小分类信息熵Eij=0，表明指标j对于方案分类做出了最大贡献。显然聚类系数各分量越趋于均衡，表示灰度越大，提供用于分类的信息越少，其分类信息熵越大，对分类所作贡献越小，应赋予指标j越小的权重；反之其分类信息熵越小，表示灰度越小，其提供用于分类的信息越明确，对分类所作贡献越大，则应赋予指标j越大的权重。

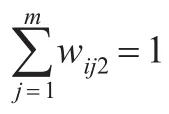
2 合理确定灰类综合决策测度权系数

2.1 目前灰类综合决策测度权系数的确定与不足

在灰色聚类决策中，合理确定指标权重，是希望较为客观合理的将待评价方案归入事先确定的灰类中，但如果还需要进一步对待评价各方案进行优劣排序，就必然涉及综合决策测度的计算问题，自然也就需要考虑灰类综合决策测度权系数的确定问题，不同的灰类综合决策测度权系数将导致各评价方案的综合决策测度发生变化，有可能引起评价方案优劣排序的顺序发生变化，因此合理确定灰类综合决策测度权系数亦显得非常重要。

刘思峰等为对属于同一灰类的多个评价方案进行排序，设置的灰类调整系数（其实质体现的就是综合决策测度权系数），对评价方案所属灰类赋予较大的调整系数，与方案所属灰类距离越远的类赋予越小的调整系数[5]，如果实际评价问题中事前设置的灰类为无序类，这种设计思想存在一定的合理性，但事实上几乎所有的评价与决策问题，事前设置的灰类均为有序灰类，对有序灰类而言，如果评价方案不属于最优类，刘思峰等的设计就会出现优类的调整系数小于比其更差的灰类的调整系数，这显然是错误的。在灰色聚类决策中更常见的情况是综合决策测度权系数由评价者直接给出，而这种确定则带有很大的随意性与主观盲目性。

2.2 灰类综合决策测度权系数的客观确定

在灰色聚类决策中，综合决策测度权系数实质上反映的是各有序灰类之间的相对重要性，换句话说反映的是各有序灰类对综合决策测度的相对贡献大小。事实上当各分指标的重要性权重与各分指标不同灰类的中心值确定时，相对较为客观合理的综合决策测度权系数就已经被隐含在里面。在实际应用中，可以将隐含权系数求出来直接作为综合决策测度权系数 η(η1，η2，…，ηs)，或将隐含权系数作为评价者确定综合决策测度权系数的重要参考依据，求取隐含综合决策测度权系数的具体步骤如下：

从设置的各分指标白化权函数中，获取能代表不同指标各灰类的中心值。对典型白化权函数，对三角白化权函数或上限白化权函数，其中心值均为，对下限白化权函数，其中心值为

（2）对各分指标灰类中心值进行规范化处理，规范后的各分指标灰类中心值记为。

如果各分指标的意义、量纲不同或指标的取值在数量上相差悬殊，在求解隐含综合决策测度权系数前，应先对各分指标灰类中心值进行规范化处理。假设评价指标均为效益性的正指标，因为成本性的指标总可以用取其倒数的方法换算为效益型指标，另设为指标j的最优类s的所属区间，如果为确定有界值，则可取，并可直接利用式（5）进行规范化，但如果为无界值，则需要从参与聚类对象的角度或所有同类对象的大环境角度用合理估算的数值作为该指标的最大值maxxj，然后利用式（5）进行规范化。

（3）求隐含的各灰类综合决策测度权系数

依据经规范化处理的各分指标中心值及分指标的重要性权重，利用式（6）求各灰类的加权中心值或称期望值Ek(k=1，2，…，s)，各灰类的期望值本身反映的就是各有序灰类间的相对重要性大小，故不同灰类的期望值Ek即为隐含的各灰类的综合决策测度权系数。

3 实例分析

随着高校实验室不断呈现的专业化、大型化和复杂化趋势，以及近几年来高校实验室相继发生的一件件触目惊心的火灾、爆炸事故，实验室的火灾危险性评价也越来越受到各高校的重视。某高校对其拥有的4个综合型实验室（A1，A2，A3，A4），利用灰色聚类决策来评价其发生火灾的危险性，评价采用的5个指标分别为建筑物属性与结构（U1）、消防设施与报警系统（U2）、安全疏散设施（U3）、可能引火源隐患（U4）、安全管理及其他（U5）[6]。

该校组织数位评价人员对各实验室火灾危险性情况进行实地检查，要求各位评价人员分别依据上述5个指标对各实验室进行打分（各指标均按百分制打分，评分越高表明指标的危险性越小，安全性越高），最后经统计处理得到的4个实验室各指标评分见表1。

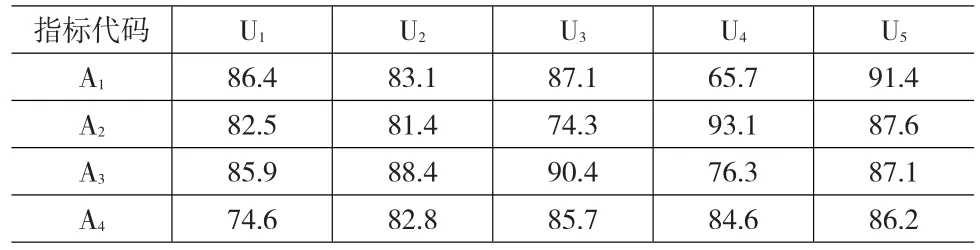
表1 4个实验室各指标的评分表

对实验室的火灾危险性评价，该高校设置高、较高、一般、低四个灰类的危险性等级，并设置以中心点三角白化权函数为核心的混合白化权函数，各分指标对灰类的白化权函数见表2所示，为书写方便，白化权函数，在表2中简写为形式。考虑到火灾危险性评价是一个系统性问题，任何方面都不容许一点马虎大意，故当任何实验室的任一指标评分值小于“高”危险性等级白化权函数的最小临界值时，无论其他指标评分高低，直接确定该实验室发生火灾的危险性评价结果为“高”危险等级。

表2 各指标对灰类的白化权函数表

3.1 计算火灾危险性评价各指标的权重

（1）利用层次分析法确定各指标的重要性权重

要采用层次分析方法确定指标权重，首先需要选择合适的判断矩阵标度，目前关于层次分析法的标度已有十多种，徐泽水通过对常见的几种标度的模拟，认为10/10～18/2标度性能最好[7]。关于该高校实验室的火灾危险性评价，便采用见表3所示的10/10～18/2判断矩阵标度。

评价人员经充分讨论，建立评价各指标间的判断矩阵，并利用方根法对判断矩阵进行计算与检验，判断矩阵及其计算结果见表4所示。

表4 评价指标的判断矩阵及其计算结果

由表4可知，5个指标的重要性权重分别为：W11=0.113，W21=0.189，W31=0.154，W41=0.301，W51=0.243。

（2）利用信息熵确定各指标的分类性权重

以实验室A1为例，将表1中5个指标的评分值代入表2相应各灰类的白化权函数，得到各指标的聚类系数见表5所示。

表5 实验室A1各指标聚类系数表

由表5可知，本文设计的各指标白化权函数，满足使各指标的聚类系数合计值等于1，故可将表5中的数据直接带入式（3）来求各指标的信息熵，得到指标1的信息熵为E11=-1 log4×(0.573×log0.573+0.427×log0.427)=0.492，同理得：E12=0.404，E13=0.0.354，E14=0.476，E15=0.433。将各指标的信息熵代入式（4），得实验室A1各指标的分类权重分别为：W112=0.179，W122=0.210，W132=0.227，W142=0.184，W152=0.200。其他实验室各指标的分类权重计算与实验室A1相同，4个实验室各指标的分类权重计算结果见表6所示。

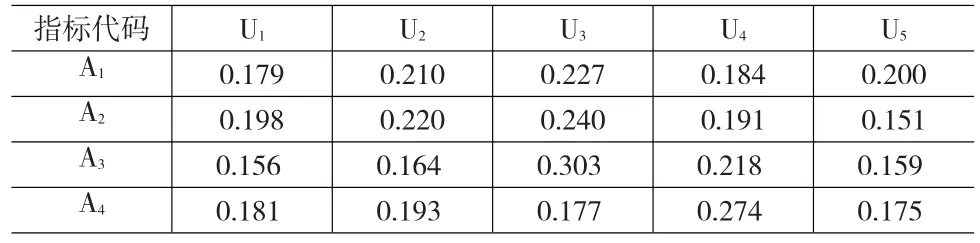
表6 4个实验室各指标的分类权重表

（3）确定各指标的组合权重

在对实验室的火灾危险性评价中，该高校评价组相对更加重视重要性权重，并确定重要性权重系数α=0.7，利用式（1）得4个实验室各指标的组合权重见表7所示。

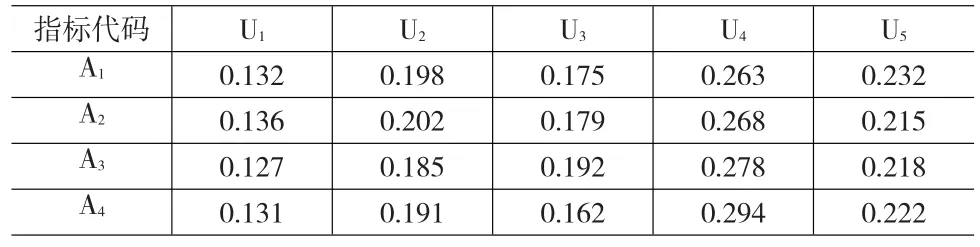
表7 4个实验室各指标的组合权重表

3.2 计算4个实验室综合聚类系数并按“最大隶属度”原则进行聚类

3.3 求4个实验室的火灾危险性综合决策测度并排序

（1）确定客观合理的灰类综合决策测度权系数

因本实例中各指标的含义、量纲均相同，规范化后的中心值为原中心值的1/100，是否进行规范化不会影响综合决策测度权系数的相对重要性，故可省略该过程。

②求隐含的各灰类综合决策测度权系数

以第一灰类为例，其该灰类的期望值E1=0.113×25+0.189×35+0.154×32.5+0.301×45+0.243×35=36.5 ，同理得E2=69.00，E3=81.34，E4=93.76。

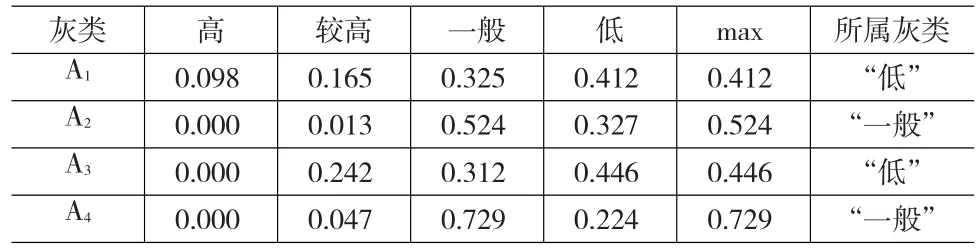
表8 4个实验室的综合聚类系数及聚类结果

该高校评价组人员认为各灰类的期望值对相应灰类的综合代表性比较符合实际，故直接以求出的隐含权系数作为综合决策测度权系数，即 η =（36.50，69.00，81.34，93.76）。

（2）对4个实验室的火灾危险性进行排序并进行分析

利用综合决策测度权系数和表8中的数据，计算得4个实验室的综合决策测度分别为80.03，74.18，83.89，83.54，从而得到4个实验室的火灾危险性排序从低到高为实验室A3，A4，A1，A2。将排序结果与表8聚类结果对比发现，实验室A1排序为3，但属于“低”危险类，实验室A4排序为2，但属于“一般”危险类，出现了排序与聚类的不一致现象。究其原因是因“最大隶属度”原则是一种较为粗略的聚类原则，聚类时仅考虑隶属度向量中的“最大隶属度”，而对隶属度向量中的其他分向量完全不予考虑，考虑问题片面所致。

基于上述分析，本文对4个实验室的火灾危险性重新设计原则聚类，依据4个实验室的综合决策测度与各灰类期望值的各自距离来归类，并将各实验室归入综合决策测度与其期望值最小距离的灰类。以实验室A1为例，实验室A1的综合决策测度（80.03）分别介于“较高”与“一般”灰类的期望值69.00和81.34之间，其综合决策测度与“较高”与“一般”灰类的期望值的距离分别为11.03和1.31，当然与“高”和“低”灰类的距离（43.53和13.73）一定大于11.03，故实验室A1属于“较高”与“一般”灰类之间，但更偏向于“一般”，按“最小距离”原则实验室A1属于“一般”危险类。同理可计算其他实验室与各灰类期望值的距离，按“最小距离”原则得实验室A2属于“较高”危险类，实验室A3和A4均属于“一般”危险类，该聚类结果与排序没有出现冲突，说明“最小距离”聚类原则考虑问题更加全面，更具合理性。

4 结语

本文分析了目前灰色聚类决策问题中指标权重确定的情况，并针对指标权重确定的不足提出组合权重的思想，将用层次分析法确定的指标重要性权重与信息熵法确定的分类性指标权重进行组合，以组合权重为基础进行评价方案的聚类，同时提出以重要性指标权重与所有指标各灰类中心值为基础的综合决策测度隐含权系数的确定步骤，最后通过某高校实验室的火灾危险性评价应用，验证了其效果的合理性。

[1]邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987.

[2]刘思峰.定权灰色聚类评估分析—灰色系统新方法[M].北京:农业出版社,1993.

[3]王正新,党耀国,刘思峰.基于白化权函数分类区分度的变权灰色聚类[J].统计与信息论坛,2011,（6）.

[4]彭安华.基于灰色聚类模型的实验成绩评定[J].淮海工学院学报(自然科学版),2010,（1）.

[5]刘思峰等.灰色系统理论及其应用（第三版）[M].北京:科学出版社,2004.

[6]贾海林,余明高,崔志恒.基于模糊层次分析法的高校实验室火灾危险性评价[J].实验室研究与探索,2010,（2）.

[7]徐泽水.关于层次分析中几种标度的模拟评估[J].系统工程理论与实践,2000,（7）.