基于线性ARIMA与非线性BP神经网络组合模型的进出口贸易预测

陈 蔚

（洛阳师范学院，河南 洛阳471022）

0 引言

进出口贸易是拉动经济增长和实现对外交流的重要工具，多年来我国对外贸易尤其是出口贸易迅速增长，但随着国际形势的日益复杂化和产业竞争力的偏弱，贸易摩擦仍然十分严重。国家积极出台各项产业结构调整和外贸政策，努力振兴企业信心，实现对外贸易的平稳增长，根据商务部发布的报告与海关总署的统计数据，2014年前3个季度，进出口、进口、出口累计增速为7.7%、8%及7.3%，9月外贸增速仅为3.3%，较七八月份的7.8%和7.1%的增长水平大幅回落，其中出口更同比下降0.3%，上半年进出口增速波动较大，这种短期中的波动同样体现于对外贸易的长期运行中。所以，有必要建立合理的数学模型对进出口贸易的走势做出预测，目前采用较多的方法是基于计量经济学的回归预测方法和序列自回归方法，但这些方法的缺陷在于一是难以完全搜集到影响进出口的所有因素，从而造成变量遗漏，其次只提取了线性规律而对非线性规律则无法进一步进行挖掘，所以本文拟采用ARIMA模型和BP神经网络模型从两个角度进行时序分析，以达到高精度预测的目的。

1 模型方法

1.1 ARIMA模型

基于时间序列的随机特性，自回归移动平均模型（ARIMA）能够很好的描述变量发展规律并进行预测。对于序列yt,可以用一个自回归过程AR(p)和一个移动平均过程MA(q）刻画其自相关结构，记为：

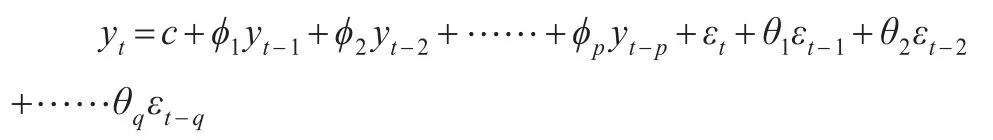
其中p，q为滞后阶数，εt为白噪音序列，具有独立同分布和服从期望为零、方差既定的正态分布。对于上式，引入滞后算子L，形成滞后多项式形式：

记

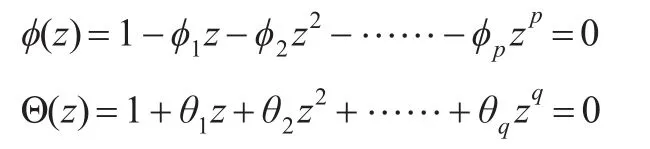
如果φ(z)特征根的倒数全部落于单位圆之内（特征根倒数模小于1），意味着满足平稳性要求，pj(j=1，2，......m)特征根倒数有相应特征意味着满足可逆性要求。对于平稳性序列，确定的过程依赖于相关系数图，AR(p)的自相关AC系数呈现出正弦或指数型减弱，然后逐渐收敛于0（拖尾性），偏自相关系数PAC则在一定阶数后为0,（截尾性），MA过程具有相反特征。

ARIMA模型的估计步骤为:首先进行单位根检验，如果非平稳则需要进行对数或差分处理形成平稳序列，其次对平稳序列建模要确定自回归和移动平均的项数ai，根据AC和PAC判定截尾和拖尾状态，但在实践中，因为拖尾性和截断性不明显，理论界提出了不同的标准，高常水(2011)认为应当满足三个要求：（1）估计系数全部显著，（2）平稳性和可逆性要求，（3）随机误差项为白噪音。但是，樊欢欢（2009）认为ARIMA模型变量估计系数t统计量要求没有OLS那么严格，只要方程拟合系数和稳定性统计量F值显著即可。最后，进行模型估计并按照残差最小化原则进行动态和静态预测。

1.2 人工神经网络BP算法

BP人工神经网络是一种多维映射关系所得出的一种误差自动修复机制，Rumelhart（1986）提出的该智能算法流程图如图1所示。

图1 BP神经网络

在BP网络中，信息的递入从输入层开始，每一层的单个神经元与下一层中所有单元进行连接，但同层之间无联系，下一层神经元得到的信息量实际是上层神经元信息输入的加权平均值和本身具有的阈值之和。在输出层，实际输出与预期输出间的差异形成了误差值，利用梯度下降理论以反向态势输入误差信息并对神经元间权重及阈值进行调整，以实现误差最小化。具体过程为：

（1）第一层中节点的信息输入为：pj(j=1，2，......m)，第二层第i节点接受信息冲击为：

（2）ai为阈值，经过转换函数处理后第二层i神经元输出为：

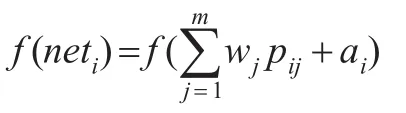
（3）第三层神经元k信息冲击：

bk—j的阈值，最终网络输出为：

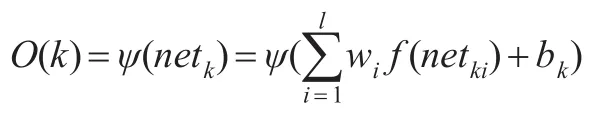
本文拟先用ARIMA模型对进出口贸易数据进行拟合，得到误差项后进行BP网络建模，形成非线性预测结果，最后综合“线性+非线性”结果，与实际值进行比较并检验。

2 我国进出口总额的实证预测

2.1 序列的单位根检验

本文研究对象为1990～2013年进出口贸易总额（单位：亿元），进行自回归移动平均模型处理的前提是序列平稳，同时为了消除波动影响，对序列进行自然对数处理。对进口额（JK）和出口额（CK）求对数后得到：LnJK=log(JK),LnCK=log(CK)。单位根检验如表1所示。LNCK和LNJK序列的ADF单位根检验值为-1.795、-1.976，均大于1%、5%、10%检验水平的临界值，故不能拒绝“包含单位根”的原假设。对两个序列进行1阶差分后的检验值分别为-4.539和-3.721，分别小于1%和5%检验水平下的临界值，认为至少在5%检验水平拒绝“存在单位根”的原假设，即进出口额服从I（1）过程。对2阶差分序列进行检验后发现t统计量更加显著，伴随概率均为0.0000。

表1 单位根检验

2.2 ARIMA模型识别与估计

针对D2（LNCK）和D2（LNJK）序列作自相关系数图，D2（LNCK）的偏自相关系数在1、2阶超过95%的置信区间之外，其他阶的PAC系数在区间之内，说明在2阶截尾，自相关系数在1阶超过虚线，故可对LnCK建立ARIMA(2,2,1)。D2（LNJK）的PAC系数在2阶很接近虚线，其他阶均在95%置信区域之内，自相关系数一直在区域之内，故本文对LnJK建立ARIMA（2,2,0）模型。

图2 出口额2阶差分序列自相关图

图3 进口额2阶差分序列自相关图

以滞后算子多项式计算得到的公式(出口额）分别为：(1-0.0004φ1L+0.128φ2L2)D2(LNCK)t=-0.008+(1-0.997L)εt

计算得到的AR（p）和MA（q）的特征根的倒数分别为-0.36i，0.36i，说明模型是稳定的，MA Roots倒数为1，未处于单位圆外，故模型具有可逆性。模型的AIC和SC信息值分别为-0.454，-0.255。

得到的公式（进口额）为：

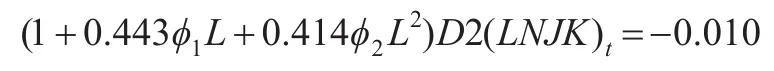
AR（P）特征根倒数为-0.22-0.060i，-0.22+0.060i，均处于单位圆之内。模型的AIC和SC信息值分别为-0.503，-0.354。

2.3 线性预测结果

表2第2、3列是用ARIMA模型估计出的我国进出口额的自然对数后二阶差分项预测值，目前在EVIEWS中没有还原选项。本文采用MATLAB7.0软件进行还原操作，结果第4、5列。第6、7列为进口与出口的实际数据。第8、9列为预测误差，是用实际值减去预测值得到。最后两列为预测相对误差，可以看出，使用ARIMA模型得到的拟合效果并不好，1995～2013年间出口与进口额的预测相对误差分别为18.43%和47.62%。

2.4 BP神经网络误差预测

根据张宇青等人（2013）的做法，将采用“滚动建模法”，即使用既定区间内5年的数据作为单次输入，然后采用区间下年（第六年）的数据作为输出，建立输入节点为5、输出节点为1的BP网络，学习样本个数为14个。使用MATLAB7.0软件对CKE和JKE进行BP网络建模，第一层和第二层节点处理函数设置为双曲正切型S函数，第三层设置为纯线性函数，训练函数采用共轭梯度方法。图4显示在训练次数达到246次后，CKE建立的BP网络训练误差收敛至一个很小的值，网络建立有效。利用建立好的网络，将2009～2013年的误差作为输入，得到2014年CKE为13721，然后采用2010～2014年误差作为输入，得到2015年误差为7962.5，依次类推，得到2016～2018年CKE预测值，分别为23522、26336、29621，将得到的预测误差CKF加上ARIMA模型预测的数值CKF，就得到了2014～2018年的出口贸易额数值，分别为129011.1、128938、149341.36、156035.48、162137.81。图5为JKE序列的BP网络训练收敛结果，在287次迭代后误差迅速收敛至一个较小的水平。计算出对应JKE数值，并还原预测值，得到结果如表2下方所示，2014年我国进口贸易额预测值为253867.72亿元，与现实情况有悖，属于突变点，但2015～2018年进口贸易额显示相对合理，预计在2018年达到了192600.18亿元。

3 结论

本文使用自回归移动平均模型（ARIMA）和人工神经网络（BP）对我国进20年来进出口贸易时间序列的线性与非线性规律进行挖掘，并对2014～2018年我国贸易状况进行预测，结论如下：

表2 我国进出口ARIMA预测结果与误差

图4 CKE网络训练结果

图5 JKE网络训练结果

（1）ARIMA和BP神经网络能够分别对国际贸易额序列中的两类规律进行挖掘，对于线性规律，可以分别用ARIMA（2,2,1）和ARIMA（2,2,0）模型对出口、进口的对数二阶差分序列进行建模，从预测结果看，ARIMA模型的精度较低，预测相对误差分别为18.43%和47.62%。使用BP方法能够充分挖掘非线性信息，根据网络训练后的预测误差能够迅速收敛到一个很小的水平。

（2）我国多年来一直处于贸易盈余状态，出口高于进口导致外汇储备增加，给人民币升值制造了压力，也对通货膨胀有着推波助澜的作用，出口作为拉动经济增长的马车之一，为促进经济社会发展、增强国力作出了很大的贡献，但不可否认的是我国贸易出口总量规模庞大的背后是质量的担忧，劳动密集型和低技术产品占总出口的比例很大，以低劳动力、原料成本为基础的出口增长是无以为继的。根据本文预测结果，在未来几年出口与进口保持上涨趋势，但从总量上进口将超过进口，造成贸易逆差。

[1]高常水，李尽法，许正中.基于ARMA模型的我国政府行政成本支出研究(1978～2009)[J].华东经济管理，2011，（1）.

[2]樊欢欢.EViews统计分析与应用[M].北京：机械工业出版社，2009.

[3]雷可为,陈瑛.基于BP神经网络和ARIMA组合模型的中国入境游客量预测[J].旅游学刊，2007，（4）.

[4]张宇青，易中懿，周应恒.一种线性ARIMA基础上的非线性BP神经网络修正组合方法在粮食产量预测中的运用[J].数学的实践与认识，2013，（22）.