大中华区股市波动的相关性及动态联动性研究

杨桂元，罗 阳，方媛媛

（安徽财经大学 数量经济研究所，安徽 蚌埠 233030）

0 引言

随着国际金融一体化，每一个股票市场并不是独立运行的个体，由于世界各地的经济联系日益增强，以及一地区企业在其他地区股票市场交叉上市等因素的影响，各地股票市场是相互联系的。由此，一个地区的股市都会或多或少与其他地区的股市之间存在相关性以及联动性。

而大中华区中的中国大陆、香港和台湾地区的股票市场中，台湾和香港的股票市场有着比大陆更长的发展历史。随着香港回归，大陆股票市场的逐步成熟以及证券市场的逐步开放，2008年以来两岸积极的经济政策等因素的影响，大陆股市和香港、台湾股市之间的联系也在逐渐增强。由此，对大中华区四个股市关系的准确把握，这对于投资者构造多样化投资组合，以及区域内相关部门政策的制定，都是非常有必要的。

本文用多元对角VECH-GARCH模型分析整个大中华区四个股市之间的相关关系，用多元DCC-GARCH模型分析它们之间的动态联动性。以完善大中华区股市间相关性的研究。

1 GARCH模型族理论及相关波动性理论

1.1 多元对角VECH-GARCH模型及波动的相关性介绍

（1）股市间波动的相关性介绍

一个股票市场可能受自身的影响而产生波动，也可能会受别的股市波动的影响而产生波动。对于这种相关关系，常用的方法是对资产收益率的条件方差和条件协方差进行建模，来刻画各金融市场间的波动相关性，而多元对角VECH-GARCH模型在分析这种相关性具有重要的作用。它的方差方程中，既包含各自变量的单项GARCH方差，也包含它们之间的协方差。以此来判定这些变量之间的大致相关关系。

（2）多元对角VECH-GARCH模型

设ut表示一个k×1维随机向量序列，且有ut|Yt-1服从N(0，Ht)分布，Yt-1是到t-1时刻的信息集，Ht是k阶正定矩阵。Bollerslev（1988）提出了一个一般的条件协方差多变量VECH模型的限制形式。均值方程为：

方差方程为：

式中：算子“·”表示两个矩阵的元素与元素乘积（Hadamard算子）。系数矩阵M、P和Q都是k阶的对称矩阵。可以利用不同的方式确定系数矩阵的参数，本文采用的是无限形式（Indefinite Matrix）：

向量ARCH类模型主要是研究Ht的不同动态特性。确定参数的最常用的方式是允许矩阵中的参数无限制的变化，即用无限制矩阵来确定参数。模型可以构造如下：

式中(Ht)ij就是矩阵Ht中的第i行，第j列元素。因为系数矩阵M、P和Q都是k阶的对称矩阵，式(3)中的每个矩阵包含了k(k+1)/2个参数。

以二元对角VECH模型为例，令矩阵M为方差方程中常数项的系数矩阵，矩阵P为方差方程中ARCH项的系数矩阵，矩阵Q为方差方程中GARCH项的系数矩阵(因为系数矩阵M、P和Q都是对称矩阵，式(3)中的每个矩阵包含了2×(2+1)/2=3个参数)。方差方程可以表示为：

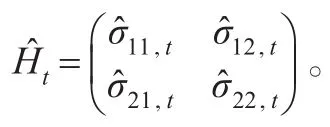
三个系数矩阵的估计结果分别为：

矩阵P̂的各个元素表示了各变量的上一期残差的平方之间相互影响，而矩阵Q̂的各个元素则表示了各变量的上期方差和协方差之间的相互影响关系。写成方程形式，则方差方程为：

第一个变量的方差方程：

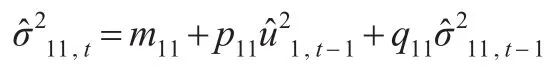
第二个变量的方差方程：

这两个方程中，满足约束条件每个方程的上期残差平方项和方差项的系数之和都小于1。

条件协方差方程：

1.2 多元DCC-GARCH模型及波动的联动性介绍

（1）股市间波动的联动性介绍

股票市场的联动性，指股票市场之间存在着明显的收益率波动的关联性，即一个股票市场产生波动，会引起另外一个股票市场的变动。相关系数是解释金融市场之间联动效应的一个很重要指标，而且市场间的相关系数并不是静态固定不变的，是随时间发生变化的，DCC-GARCH模型正是分析动态相关关系的重要模型。

（2）多元DCC-GARCH模型

Engle(2002)提出了DCC-GARCH模型，它是常条件相关系数(CCC-GARCH模型)的进一步拓展。与其他多元GARCH模型一样，可以克服异方差性的影响。可以用来估计多个资产之间的动态相关关系。

设k种资产收益rt服从均值为0，协方差矩阵为Ht的多元正态分布。

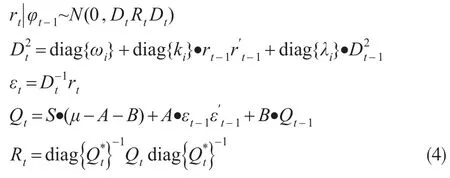
其中，φt-1为截止到t-1时期所有可能获得的信息集合；是一个对角矩阵，对角线上的元素为各单变量的条件方差；S为标准化残差εt的无条件协方差矩阵；Rt为条件相关系数矩阵；符号“·”表示矩阵对应元素的点乘；Qt为标准化残差的条件协方差矩阵；为对角矩阵，对角线元素是Qt对角元素的平方根。

模型的参数采用最大似然估计，估计过程分两步进行。首先对各个单变量分别进行GARCH模型得出个单变量的条件方差和残差序列。之后利用条件方差标准化残差序列估计多元DCC-GARCH模型的条件相关系数矩阵Rt。根据Rt来分析大中华区股市的联动性。

2 实证检验

2.1 数据的选取

在分析股市间的相关性及传递性时，本文首先分别选取上证综合指数、深圳成分指数、香港恒生指数、台湾加权指数的日收盘价格指数2006年1月4日至2013年2月28日的数据。再计算其收益率，公式为：

其中i取1、2、3、4分别表示上海、深圳、香港、台湾股市。Ri，t为i市场的收益率序列，Pi，t表示第i市场第t日的收盘价。即分别用上海综指收益率{RSH}、深圳成指收益率{RSZ}、香港恒生收益率{RHK}、台湾加权收益率{RTW}作为变量来进行建模分析。

由于大陆、香港、台湾的节假日不同，需要把数据对齐。选取四个股市都开盘的交易日，剔除掉有股市不开盘的交易日的收益率数据，共1649组数据。以此得到的收益率数据，来分析股市间的相关性及传递性。

2.2 对各收益率序列统计分析及ARCH效应检验

大中华区各股市收益率序列的时序图如图1所示。从时序图中可以很直观的看出，各股市收益率序列都出现波动率的聚集现象，即方差在一定时段中比较小，而在另一时段中比较大。

图1 大中华区股票市场收益率序列时序图

大中华区各股市收益率序列的描述性统计如表1所示，由J-B统计量可知，在1%的显著水平下，四个股市的收益率序列都显著不服从正态分布；由偏度值可知，上证综指、深圳成指、台湾加权指数都呈左偏态势，香港恒生指数呈右偏态势；四个股市的收益率序列的峰度值都明显大于3，尖峰特征非常明显。因此，大中华区各股市收益率序列分布都呈现出明显的尖峰厚尾现象。

如果对非平稳时间序列进行建模，往往会出现虚假回归问题。所以对这四个收益率序列进行建模之前，需要先对它们进行平稳性检验。本文分别选用ADF平稳性检验和PP平稳性检验。检验结果如表2所示。

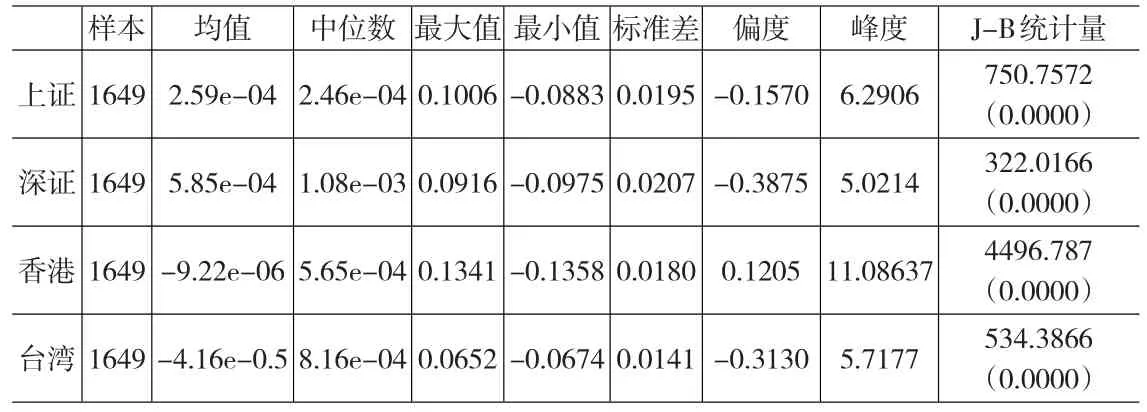
表1 收益率序列基本统计特征

表2 收益率序列平稳性检验

由检验结果可知，在1%显著水平下，只含有截距项、截距项加趋势项、不包含截距项与趋势项的任何形式的平稳性检验，ADF平稳性检验和PP平稳性检验都拒绝了这四个收益率序列有一个单位根的零假设。说明大中华区各股市收益率序列是平稳的，可以直接对它们进行建模。

收益率序列的自相关性确定均值方程；收益率的平方序列相关性确定是否存在非线性相关性，波动集聚现象是否明显。其序列相关性检验及ARCH-LM检验结果如表3所示。

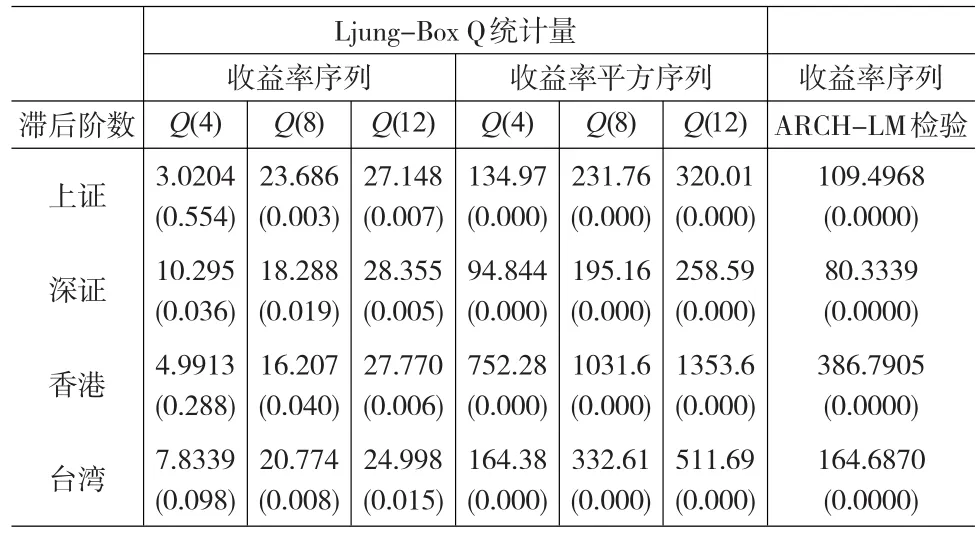
表3 收益率序列及收益率平方序列的相关性检验及ARCH-LM检验

由表3可知，在5%显著水平下，上海，香港，台湾股市收益率序列短期不存在自相关性，而长期都存在自相关。深圳股市收益率序列不管长短期都存在着自相关。收益率平方序列的Q统计量不管长期还是短期，大中华区各股市都非常显著，表明这四个收益率序列存在着非线性自相关。且由ARCH-LM结果可知，四个收益率序列都存在异方差的特性，因此考虑建立多元GARCH模型。

2.2.1 基于对角VECH-GARCH模型的相关性分析

利用上证综指、深证成指、香港恒生指数、台湾加权指数收益率数据两两建立二元GARCH(1,1)模型，在估计过程中，选择的模型类型为对角VECH模型。其中建立上海-深圳股市VECH模型的均值方程中，上海股市自变量有rsh(-2)，深圳股市自变量有rsz(-1)；建立上海-香港股市VECH模型的均值方程中，上海股市自变量有rsh(-6)，香港股市自变量有rhk(-6)；建立深圳-香港股市VECH模型的均值方程中，深证股市自变量有rsz(-1)，香港股市自变量有rhk(-10)；建立上海-台湾股市VECH模型的均值方程中，上海股市自变量有rsh(-6)，台湾股市自变量有rtw(-1)；建立深圳-台湾股市VECH模型的均值方程中，深圳股市自变量有rsz(-6)，台湾股市自变量有rtw(-1)；建立香港-台湾股市VECH模型的均值方程中，香港股市自变量有rsh(-1)，台湾股市自变量有rsz(-1)。

均值方程不是本文关注的重点，而可以从方差方程得出两个股市间的相关关系，所以本文重点列出方差方程的估计结果。对于沪、深、港、台之间的VECH模型的方差方程结果如表4所示。

表4 沪深港股市间的VECH模型估计结果

为保证建立的模型正确，需要对模型的残差进行必要的检验，由表4可知，标准化残差都接受了ARCH-LM检验的原假设，表明各残差都不存在ARCH效应(异方差性)，说明模型的建立是合理的。

在以上方程参数中，每个方程的上期残差平方项Pii，i=1，2 和方差项Qii，i=1，2 的系数之和都小于1，满足约束条件，并且系数之和都接近1，表明收益率序列受到冲击时，其影响存在着较为长久的ARCH效应（异方差）。

2.2.2 基于多元DCC-GARCH模型的联动性分析

股市之间的联动现象是国际证券市场中的一个十分重要的经济现象。对于某个地区的股票市场而言，周边地区股票市场和国际金融市场的宏观经济走势的冲击，将会改变市场之间原有的联动性，带来新一轮的联动效应。国际股票市场关联以股票市场的一体化和经济一体化为基础和依托。本文以动态相关系数来考查大中华区股市间的联动现象。如果不考虑大中华区股市收益率之间的动态关系，计算它们之间的非条件相关系数，其结果如表5所示。

表5 大中华区各股市间的无条件相关系数

由表5可知，上海股市与深圳股市的相关程度最高，为0.8351。尽管可以从相关系数中看出他们之间的相关程度，但是这些系数都是静态的，不能反应他们相关系数的变化过程。所以考虑建立DCC-GARCH模型，以观察他们之间的相关性随时间变化的过程。

建立DCC-GARCH模型，分两步进行，首先建立各单变量的GARCH模型，其结果如表6所示。

表6 对各单变量建立GARCH模型结果

由表6可知，大中华区股市的ARCH项系数与GARCH项系数之和都均小于1，满足参数约束条件，且非常接近于1，表明各股市所受的波动冲击是持续和持久的。

之后利用条件方差标准化残差序列两两估计多元DCC-GARCH模型的参数Rt。经检验，标准化残差都接受了ARCH-LM检验的原假设，表明各残差都不存在ARCH效应，模型的建立是合理的。根据DCC-GARCH模型的Rt，得出大中华区股市的动态相关关系图，如图2所示。

图2 大中华区股票市场收益率序列的动态相关关系图

由图2可知，上海股市与深圳股市的相关程度相当高，从2007年开始相关系数有显著提高，从0.6到0.7之间增加到0.85左右，并维持在此水平上下波动。这是因为2006年中国大陆基本完成股改以后，市场健康稳定运行的内在基础不断夯实，市场的投资价值正在逐步为投资者所关注，资本市场已经初步具备了实现重要发展突破的基本条件。这对沪深股市相关性的增强有着密切关系。

上海股市、深圳股市与香港股市的相关性，也是从2006年中国大陆基本完成股改之后，2007年开始分别从0.2和0.3左右上升到0.5～0.65和0.5～0.6之间，在此区间上下波动。由此我们发现，2006年基本完成股改之后，我国股市之间及与香港股市之间相关性都有着显著的提高，说明股改对我国的股市发展有着积极的意义。

上海股市、深圳股市与台湾股市的相关性，在2006～2008年间一直处于下降状态，而2008年之后，大陆股市与台湾股市的相关性有所增强，它们之间的相关系数从0.2左右分别上升到0.3～0.4之间及0.3～0.35之间，并在此区间上下波动。这可能与2008年马英九当选台湾领导人之后，两岸局势发生积极变化，两岸关系迎来难得历史机遇。两岸同胞往来之频繁、经济联系之密切、文化交流之活跃、共同利益之广泛是前所未有的。这是导致两岸股市的相关性增强的主要原因。

香港股市与台湾股市的相关系数从2006～2013年间，都是维持在0.6左右上下波动，这说明香港股市与台湾股市开市比较早且成熟，相关程度也比较稳定。其中，从2006～2013年间，共有三次重大波动。这可能是受国际股市的影响，2007年美国爆发金融危机以来香港与台湾股市的相关系数出现了第一次大的波动；到2008年8月，美国房贷两大巨头——房利美和房地美股价暴跌，持有“两房”债券的金融机构大面积亏损，香港与台湾股市的相关系数出现了第二次大的波动；2011年美国爆发了美债危机，导致香港与台湾股市的相关系数出现了第三次大的波动。由此可见，香港和台湾股市受国际股市的影响较大。

3 结束语

本文在回顾多元GARCH类模型的基础上，用多元对角VECH-GARCH模型以及多元DCC-GARCH模型分析它们之间的相关性和动态联动性，分析结果表明：大中华区的日收益率波动的条件方差之间的相互影响是持久的，在世界经济全球化背景下，大中华区股市的波动呈现出趋同的现象；2006年中国大陆基本完成股改以后，沪深股市相关性有明显的增强；而且我国股市之间及与香港股市之间相关性都有着显著的提高，说明股改对我国的股市发展有着重要的意义；2006年的股改基本完成和2008以来积极的两岸政策，导致两岸股市的相关性明显增强；而香港和台湾股市的相关性受国际股市的影响较大。

由此可见，我国有关部门应当不遗余力的落实和完善股改政策，积极发展对台湾的经济政策，加强两岸的金融交流。而且应当及时关注外部市场环境和需求的变化，有针对性的进行市场结构调整，建立健全产品体系，进一步加快金融产品的研发和创新，促进我国股票市场朝着高效安全、结构合理、功能完备的方向健康有序发展，为更好地服务国民经济，做出应有的积极贡献。

[1]樊智,张世英.多元GARCH建模及其在中国股市波动分析中的应用[J].管理科学学报,2003,6(2).

[2]谷耀,杜丽娜.沪、深、港股市信息溢出效应与动态相关关系—基于DCC-(BV)EGARCH-VAR的检验[J].数量经济技术经济研究,2006,8(1).

[3]董秀良,吴仁水.基于DCC-MGARCH模型的中国A、B股市场相关性及解释[J].中国软科学,2008,(7).

[4]王鹰翔,张鲁欣.基于向量GARCH模型的国际证券市场波动溢出研究[J].管理评论,2011,(6).

[5]Robert F，Engle.Dynamic Conditional Correlation:A Simple Class of Multivariate Generalized Autoregressive Conditional Heteroskedasticity Models[J].2002,20(3).

[6]将治平.人民币利率与汇率的动态相关关系：基于DC C模型的研究计量经济分析方法与建模[J].软科学,2008,22(7).