LDPC码译码算法研究与FPGA设计

李世超（甘肃政法学院公安技术学院，甘肃兰州730070）

LDPC码译码算法研究与FPGA设计

李世超
（甘肃政法学院公安技术学院，甘肃兰州730070）

运用线性逼近法简化LDPC码的对数似然比BP算法中的双曲正切函数和反双曲正切函数，从而达到减少该算法计算次数的目的.以简化后的算法为基础，在QuartusⅡ8.0软件平台上，用verilog语言进行LDPC码译码器的设计，用QuartusⅡ8.0软件生成RTL门级电路.仿真结果证明简化后的对数似然比BP算法的正确性与硬件可行性.

LDPC码；对数似然比BP算法；线性逼近；FPGA译码器设计

LiSC.LDPCCode Decoding Algorithm and FPGA Design[J].Journalof Yibin University,2015,15（6）：76-80.

随着经济的发展和科技的进步，人们对通信质量的要求也在日益增加，总是希望找到一些能够提高通信质量的方法.对于无线通信而言，纠错码的性能会直接影响到通信质量.提高通信质量所追求的目的就是提高信息传输的有效性与可靠性，而纠错码正是提高信息传输可靠性的重要方法之一.低密度奇偶校验码（LDPC码）实现复杂度较低且性能接近于香农极限[1-4]，业界学者广泛认为LDPC码将是第五代移动通信纠错码的首选[5].LDPC码已经成为目前编译码界研究的热点[5].

1　LDPC码译码算法简介

LDPC码译码算法对信息传输的有效性和安全性起着至关重要的作用.如果译码算法无法正确译出所传输的信息，无论信源编码和信道编码发挥如何巨大的作用，信息也是无法正确传输的.LDPC码的译码算法多是以BP迭代算法[6]为基础改进的.

1.1BP迭代译码算法原理

LDPC码所采用的BP迭代译码算法，简单的说，就是信道估计和接收信号在给定的条件下，每迭代一次，都对有噪序列的每一个符号估算其后验概率，再将所得到的结果输入下一次进行迭代，来获得更好的结果.设码字c=（c1,c1,…,cn）经过BPSK调制后映射为x=（x1,x1,…,xn）,传输序列x通过信道后，接收序列为y=（y1,y1,…,yn），通过y可以得到译码序列ˆ.BP迭代译码算法的原理如图1所示.

LDPC码的BP算法具有如下优点：第一，在BP迭代译码算法中，并不是进行固定次数的迭代，而是当试验译码得到成功时，译码就立刻结束.这样就大大减少了迭代的次数.第二，BP算法的复杂度较低，计算量不会因为码长的增加而增加.第三，由于该算法是一种并行算法，所以当硬件实现该算法时，可以提高译码速率.

图1　BP迭代译码算法的原理框图

1.2对数似然比BP算法

BP译码算法的过程是比较复杂的.首先，该算法需要分别计算每个变量节点和校验节点比特分别为0和1的概率.这就需要很大的运算量.其次，该算法中有许多的乘法运算，如果用硬件去实现该算法会耗费大量的时间和硬件资源.考虑到这些不便，人们对BP译码算法提出了许多改进的方法，对数似然比BP算法[7]就是其中的一种.该算法最大的优点就是用加法运算代替了BP算法中大量的乘法运算，从而减少了运算所需的时间，提高了效率.

对数似然比BP算法的译码过程[7]如下：

1）初始化

首先，需要计算信道传送给变量节点的初始概率似然比L（Pi），其中i=1,2,…,n；其次，需要设定变量节点传送给与其相连的校验节点 j的初始消息.

2）迭代处理

①校验节点的更新

当迭代l次时，变量节点i传送给与其相连的校验节点j的消息的计算式可写为：

上式也可写为：

②变量节点的更新

当迭代l次时，校验节点j传送给与其相连的变量节点i的消息的计算式可写为：

③判决译码

计算所有变量节点的判决消息：

当L（l）（qi）＞0时，有ˆ=0，反之=1.

3）停止

2　对数似然比BP算法的简化

2.1双曲正切函数和反双曲正切函数的线性逼近

在对数似然比BP算法中，译码算法的复杂度主要是在更新校验节点时需要计算双曲正切函数和反双曲正切函数.因此需要先对双曲正切函数进行限幅修正，双曲正切函数tanh（x）修正如下：

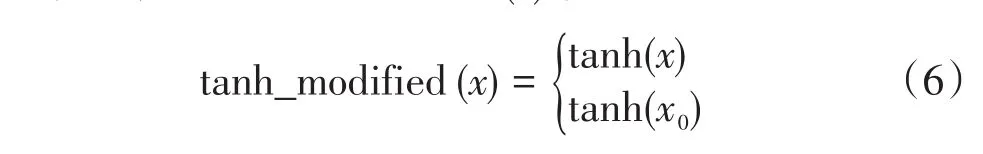
由于在（2）式中，双曲正切函数tanh（x）输入的值为L（qi′j）的绝对幅值，因此在该式中x的取值为[0∞]，而该式中的x0取值较小，即x0＜10.采用限幅方法修正以后，双曲正切函数趋于无穷的输入值被近似为tanh（x0）.其中最佳的x0值是由计算机仿真所得到的，在仿真中采用（500,3,6）的规则LDPC码，对x0=3,4,…,10的仿真结果表明，x0为3、10时译码性能衰减较大，在较高信噪比时不优于未对双曲正切函数tanh（x）修正时的性能；x0为4、5、6时，误码率性能针对于未对双曲正切函数tanh（x）修正时得到改善；x0为6、7、8、9时相对于x0为4、5的情况得到了更好的误码率性能.在本文接下来的部分中，x0选取为6.

则式（6）可写为

在双曲正切函数限幅修正的基础上进行线性逼近，其表达式可以写为：

同样的，对反双曲正切函数进行线性逼近也可以写成上式分段函数的形式.

2.2对数似然比BP算法的简化

对数似然比BP算法的主要难度在于校验节点的更新计算中存在双曲正切函数和反双曲正切函数，在简化算法中用线性逼近后的双曲正切函数和反双曲正切函数代替原算法中的双曲正切函数和反双曲正切函数.

则简化后的校验节点的更新可写为：

而其他的译码步骤和对数似然比BP算法一致，在此不再叙述.

2.3简化后的译码算法的性能仿真及分析

使用matlab仿真软件，在加性高斯白噪声的信道下，对未简化的对数似然比BP算法和简化后的对数似然比BP算法进行性能仿真，并通过仿真结果对两种算法的性能进行分析.

在本次仿真中选取（500,3,6）的规则LDPC码，采用BPSK调制方式，译码算法为对数似然比BP算法及本文简化后的对数似然比BP算法，迭代次数定为20次，则未简化的对数似然比BP算法和简化后的对数似然比BP算法的性能仿真结果如图2所示.

图2　简化后算法与未简化算法的性能比较

通过图2的仿真结果可以看出，简化后的对数似然比BP算法与未简化的对数似然比BP算法相比，误码率有较小的增加.当信噪比小于1 dB时，两种算法的性能是十分接近的，而随着信噪比的不断增加，简化后的对数似然比BP算法的误码率略高于未简化的对数似然比BP算法.当误码率为2×10-4时，简化后的对数似然比BP算法与未简化的对数似然比BP算法相比，信噪比提高了约0.08 dB.

2.4译码算法计算次数的比较

比较对数似然比BP算法和简化后的对数似然比BP算法可知，这两种译码算法的区别就在于校验节点更新的计算次数上.

通过比较这两种算法校验节点的更新表达式，可知这两种算法的每次校验节点更新的计算次数如下：

1）未简化的对数似然比BP算法

对于未简化的对数似然比BP算法，每次校验节点更新计算，需要进行dcj-1次双曲正切函数运算，1次反双曲正切函数运算，dcj-1次符号运算，dcj-1次除法运算，dcj-1次乘法运算.

2）简化后的对数似然比BP算法

对于简化后的对数似然比BP算法，每次校验节点更新计算，需要进行dcj次的双曲正切函数的线性逼近运算，dcj-1次符号运算，dcj-1次除法运算，dcj-1次乘法运算.

通过上述译码算法计算复杂度的比较可以看出，简化后的对数似然比BP算法与未简化的对数似然比BP算法相比，在校验节点更新过程中的计算复杂度有明显的下降.可见，简化后的对数似然比BP算法确实降低了运算的复杂难度.

3　简化后的LDPC码译码器的设计

3.1译码器的设计思路

LDPC码译码器的设计，主要是由校验节点、变量节点和Tanner图上的连接关系所组成.通过Tan⁃ner图可以看出，变量节点所得到的信息是由校验节点所传送的，变量节点将所得到的信息通过一定的计算，再将计算出的更新信息传递给校验节点.同样，校验节点所得到的信息是由变量节点所传送的，校验节点将所得到的信息通过一定的计算，再将计算出的更新信息传递给变量节点.LDPC码译码算法的核心就是迭代，其译码器的实质就是校验节点处理器（CNP）和变量节点处理器（VNP）进行计算并且将计算结果相互传递、更新的过程.在校验节点处理器和变量节点处理器之间要加入一个中间信息存储模块，用来进行中间信息的存储、控制和缓冲.另外，需要在校验节点处理器和变量节点处理器之间设计一个控制模块，以此来防止校验节点处理器和变量节点处理器同时工作时所产生的冲突.

3.2变量节点处理器的设计

在实际设计的过程中，变量节点处理器不但需要完成校验节点的更新处理功能，而且还应该能够完成信息的输入和输出功能.由于中间信息存储器经过初始化之后所存储的数据全部为0，因此在经过变量节点处理器的运算之后，所写入的数据应该是相应的信道信息.另外，在时序的设计上还需注意，当变量节点处理器从存储器中读取数据时，从存储器的地址到读到该地址所对应的数据时会有一个时钟周期的延时.图3即为经过QuartusⅡ8.0软件编译得到后的变量节点处理器时序仿真图.

从图3可以看出，中间信息存储器的输入信号和初始数据存储器的输入信号完全按照设计的时序每个时钟周期都进行输入.而经过变量节点处理器运算之后得到的数据，大约每隔3个时钟周期才会得到一个输出.并且从图3中也可以清楚地看到，输出信号不但出现了一定的毛刺而且还出现了不定值.经过检查，功能符合设计的要求.

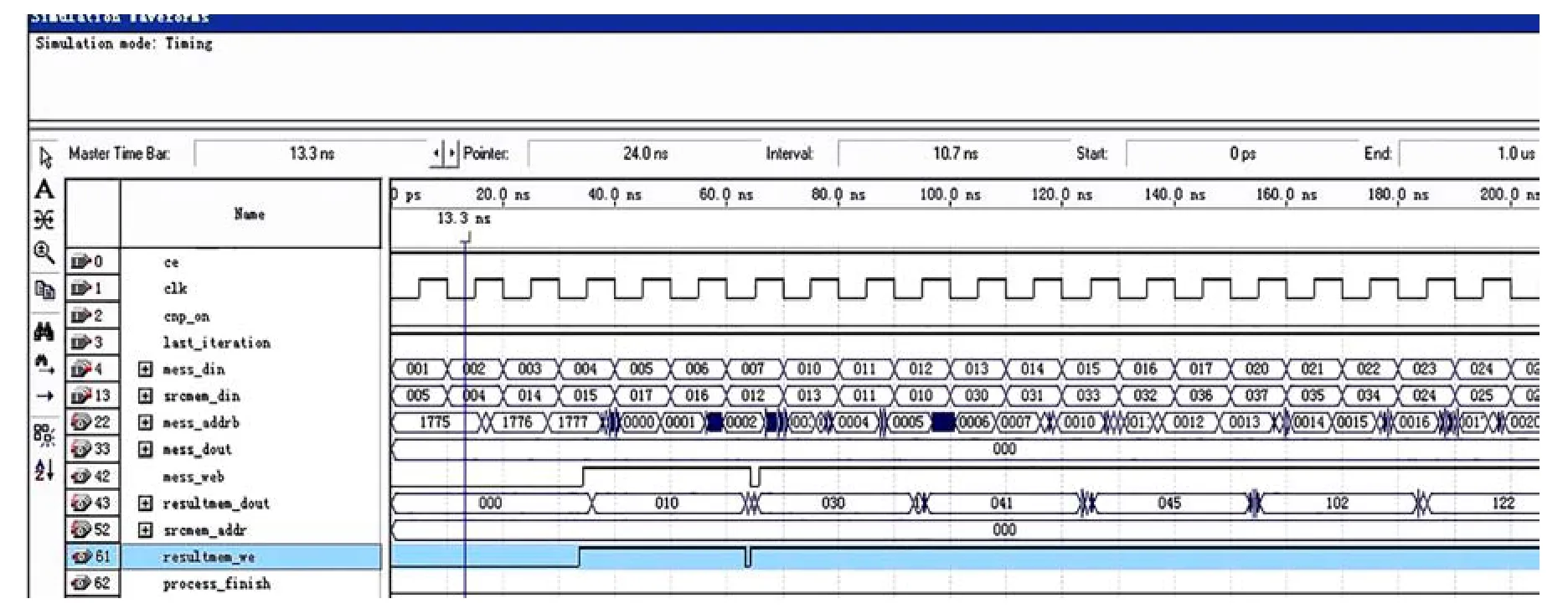
图3　变量节点处理器时序仿真图

3.3校验节点处理器的设计

校验节点处理器所完成的功能主要是校验节点数据的更新，在电路设计中需要注意的问题是，由于校验节点处理器所输出的地址首先要经过ROM才会输入到中间信息存储器，因此在时序方面会有两个时钟周期的延时.

图4即为经过QuartusⅡ8.0软件编译后得到的校验节点处理器时序仿真图.

从图4可以看出，中间信息存储器的输入信号完全按照设计的时序每个时钟周期都进行输入.而经过校验节点处理器运算之后得到的数据，大约每隔5个时钟周期才会得到一个输出.从图中还可清楚地看到，输出信号不但出现了一定的毛刺而且还出现了不定值.经过检查，功能符合设计的要求.

图4　校验节点处理器时序仿真图

3.4顶层模块的设计

对所设计的所有模块进行过仿真、且功能正确后，则对整个设计进行仿真.图5即为经过Quartus Ⅱ8.0软件编译后得到的顶层模块时序仿真图.

图5　顶层模块时序仿真图

4　结语

由于LDPC码的应用十分广泛，因此对LDPC码的硬件设计就变得十分重要.如果要对LDPC码进行硬件设计首先要考虑的就是采用何种编码和译码算法.目前，编码算法和译码算法有很多种，特别是译码算法：有些算法注重译码的速率，但译码的准确度不高；有些算法注重译码的精度，但译码速率较慢，资源消耗较大，硬件难以实现.本文正是根据这一问题，对LDPC码的对数似然比BP算法进行了简化.简化后的算法较原算法相比，极大地降低了原算法的复杂度.并以简化算法为基础，以QuartusⅡ8.0为仿真平台，设计了一种LDPC码译码器.

[1]MacKay D JC,Neal R M.Near shannon limit performance of low density parity check codes[J].Electronics letters,1996,32（186）：1645-1646.

[2]Gallager R G.Low Density-Parity Check-Codes[M].Cambridge, MA：MITPress,1963.

[3]Tanner R M.A recursive approach to low complexity codes[J].IEEE Transactionson Information Theory,1981,27（9）：533-547.

[4]Wiberg N,Loeliger H A,Kotter R.Codes and iterative decoding on generalgraphs[J].Euro Trans Telecomm,1995,6（2）：513-525.

[5]Porcello,J C.Designing and implementing Low Density Parity Check（LDPC）decoders using FPGAs[C].Big Sky：Aerospace Con⁃ference.2014：1-7.doi：10.1109/AERO.2014.6836261.

[6]McEliece R J,MacKay D JC,Cheng JF.Turbo decoding as an in⁃stance of Pearl’s‘Belief Propagation’algprithm[J].IEEE Journal on Selected Areas in Communication,1998,16（2）：140-152.

[7]Hu X Y,Eleftheriou E,Arnold DM,etal.Efficient implementation⁃softhe sum-productalgorithm fordecoding LDPC codes[C].San An⁃tonio：GLOBECOM 2001-IEEE Global Telecommunications Con⁃ference.2001：1036-1041.

（编校：李青）

LDPCCode Decoding Algorithm and FPGA Design

LIShichao
（College ofPublic Security Technology,Gansu Institute ofPolitical Scienceand Law,Lanzhou,Gansu 730070,China）

The logarithmic likelihood ratio of BPalgorithm was introduced to LDPC code.The linear approximationmeth⁃od was used to simplify the hyperbolic tangentand inverse hyperbolic tangent function in the logarithmic likelihood ratio of BPalgorithm,which can reduce the numberof the algorithm.Based on the simplified logarithmic likelihood ratio of BP algorithm and Quartus II 8 software platform,using Verilog language for the design of LDPC decoder,the RTL gate-level circuitwas generated.The simulation results prove the correctness and hardware feasibility of the simplified logarithmic likelihood ratioof BPalgorithm.

low-density parity-check codes；the logarithmic likelihood ratio of BPalgorithm；linear approximation；FPGA decoder

TN929.53

A

1671-5365（2015）06-0076-05

2015-01-28修回：2015-03-09

李世超（1986-），男，助教，博士研究生，研究方向为无线通信

网络出版时间：2015-03-17 17：16网络出版地址：http：//www.cnki.net/kcms/detail/51.1630.Z.20150317.1716.001.html

引用格式：李世超.LDPC码译码算法研究与FPGA设计[J].宜宾学院学报,2015,15（6）：76-80.