钢制球罐疲劳寿命的有限元计算

翁剑成，谢煌生，卢建湘，张雪华（龙岩学院物理与机电工程学院机电系，福建龙岩364012）

钢制球罐疲劳寿命的有限元计算

翁剑成，谢煌生，卢建湘，张雪华
（龙岩学院物理与机电工程学院机电系，福建龙岩364012）

使用通用斜率法建立16MnR的S-N曲线，借助ANSYS软件，计算出危险点的应力幅，分别根据钢制压力容器—分析设计标准公式和ANSYS后处理，求得球罐的疲劳寿命，为工业上计算寿命提供了高效的计算模式.

S-N曲线；疲劳寿命分析；有限元分析

Weng JC,Xie HS,Lu JX,etal.The Fatigue Life Analysisof the Steel Spherical Tank Based on Finite Element[J].Jour⁃nalof Yibin University,2015,15（6）：10-12.

钢制球罐支柱与球壳的连接方式中，国内外普遍采用赤道正切柱式支承，这种支承方式会产生较大的局部应力，另外，球罐经常受到内压的周期性载荷作用，在球罐的设计中，必须对其进行应力校核[1]和疲劳寿命计算.GB12337-1998《钢制球形储罐》中，对连接处应力采用一种简化处理后的计算方法.这种受力分析并不十分严密，应力最大点的选择也带有主观性.为此，本文将采用有限元方法分别进行两种载荷工况下，球罐整体应力状况分析，找出应力最大点，在此基础上，进行疲劳寿命计算，使球罐设计更加科学化.

1　球罐物理参数及疲劳设计曲线

1.1球罐的物理参数

在20℃的工作温度下，球罐本体材料16MnR，其弹性模量E=205GPa，泊松比μ=0.3，球罐中混合液化石油气的密度是583.66 kg/m3，抗拉强度为470 MPa，屈服强度为345MPa，许用应力为205MPa，如表1所示.

表1　16MnR基本物理力学性能参数和分析参数

1.2压力容器的低周疲劳设计曲线

疲劳寿命曲线Sa-N是进行压力容器疲劳安全寿命设计的重要依据，在压力容器低周疲劳中，最好采用应变作为控制变量，作出总应变幅与寿命曲线，以此来表示材料的抗疲劳性能，由Manson-Coffin公式推导可得总应变－寿命曲线，如图1所示，其数学表达式为[2]：

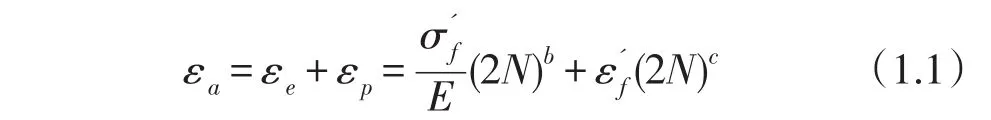
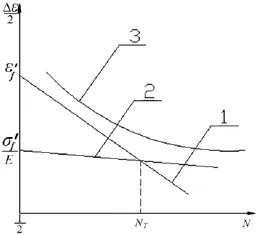
图1　应变－寿命曲线（双对数坐标系）

然而，为了更容易观察实验结果的规律性，并与高周疲劳寿命曲线坐标一致，采用“虚拟应力幅”，虚拟应力幅为

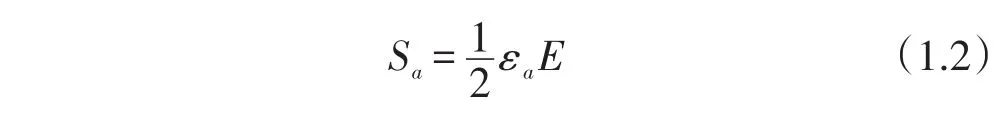
试样单调拉伸时的真实应变εf可以用试样截面收缩率ψ计算：

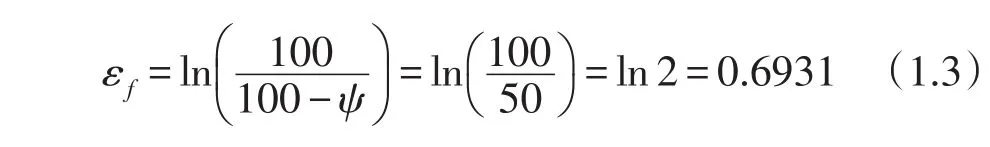
把表1弹性模量、抗拉强度数据和式（1.3）εf代入Park和Song[3]提出的修正通用斜率公式，得出材料特征参数如（1.4）式：

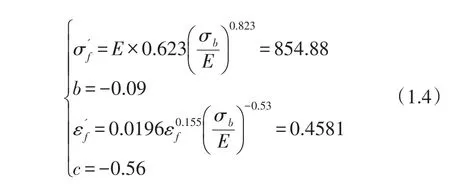
其中σb为材料的抗拉强度极限（MPa）；εf真实应变.

把（1.1）式和（1.4）式代入（1.2）式，得出虚拟应力幅Sa：

当考虑平均应力σm的影响，Sa值经修正变为值，有关系式：

分别取疲劳循环次数N为104、5×104、105、5× 105、106、5×106、107，根据公式（1.5）算出对应Sa值，如表2的第一行；根据修正公式（1.6），计算出对应值，如表2的第二行；第二行除以2得到表2第三行设计Sa；根据表2数据，基于最小二乘法原理，利用Origin软件拟合出各个应力幅与循环次数的关系曲线－疲劳设计曲线，如图2所示.

表2　应力幅结果　（单位：MPa）

图2　材料的疲劳寿命曲线

2　球罐有限元模型

2.1有限元模型的建立

球壳内径1.23×104mm，壁厚45mm，在球罐赤道部位圆周均布8根支柱，该种支柱分为上、下支柱，上支柱为U型柱，U型柱顶部为盖帽，它们均由12mm厚的钢板卷制而成，下支柱采用无缝钢管，规格为内径ϕ426mm，壁厚12mm，上、下支柱采用支撑板连接，其厚度为30mm，球壳中心到下支柱底部的高度为8 000mm.

在球罐一侧面作用风载荷情况下，球罐的物理结构是不对称的，须建立球罐整体模型.对该整体模型，文中采用高节点六面体单元SOLID186，对整个球罐模型进行网格映射划分，如图3.

2.2载荷分析

主要考虑球罐受到重力、内压、风载的情形.

采用等效密度方法将球罐附件的质量568.69× 103kg移到球壳中，经计算可求得球罐壳体的等效密度为ρ1=6.09×10-5kg/mm3.

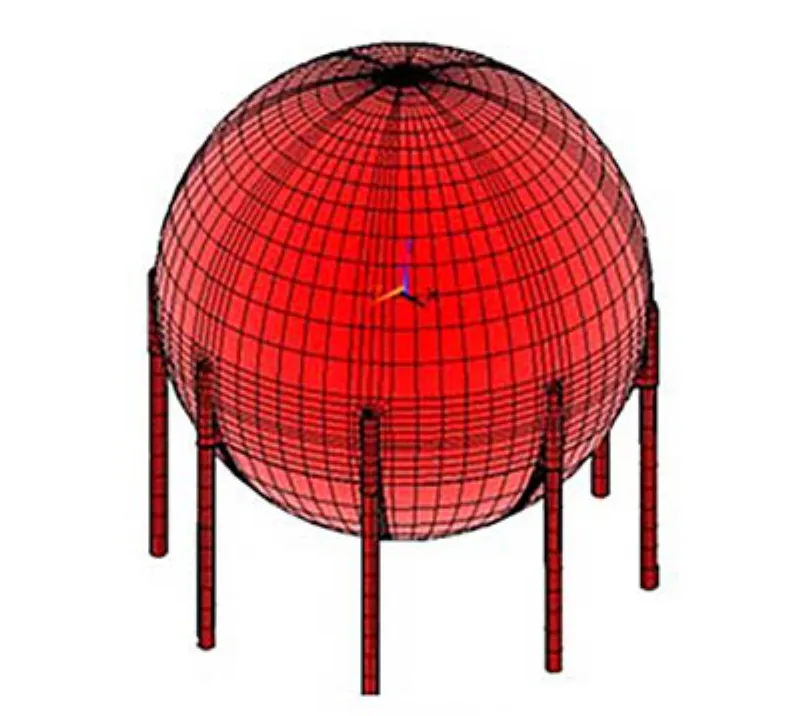
图3　网格模型

在球壳内壁建立表面效应单元SURF154，选择加载面为SURF154单元的⑤号面，施加设计压力1.7MPa.

在球壳左侧外壁迎风面，采用表面效应单元SURF154，选择加载面为SURF154单元的⑤号面，施加龙岩基本分压600 Pa[3]风载后如图4所示.

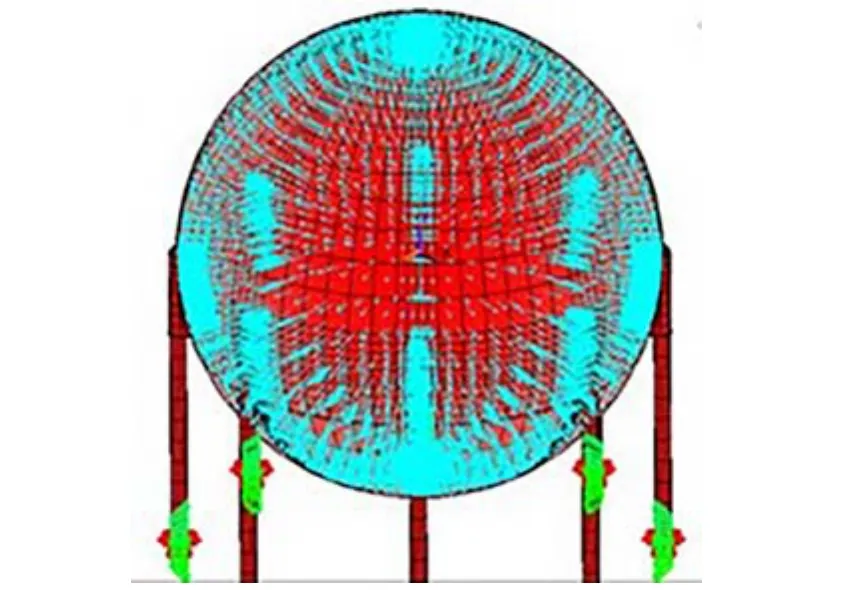
图4　自重+内压+风载

3　应力幅Sa的计算

考虑两种工况：

工况1：自重+内压+风载；在该工况下，球罐最大应力云图如图5所示，最大应力强度发生在支撑板与下支柱连接处，为342.73MPa.

工况2：自重、支柱下端按固支边界处理，约束全部位移.在该工况下，球罐的应力强度是120.24 MPa，以这点的应力为准则进行分析，其平均应力σm和应力幅Sa分别为：

σm=（342.73+120.24）2=231.49 MPa

Sa=（342.73-120.24）2=111.25 MPa

4　疲劳寿命的两种计算

4.1疲劳寿命经验计算

由有限元计算出应力幅Sa=111.25，按照表1中给出的数据有：

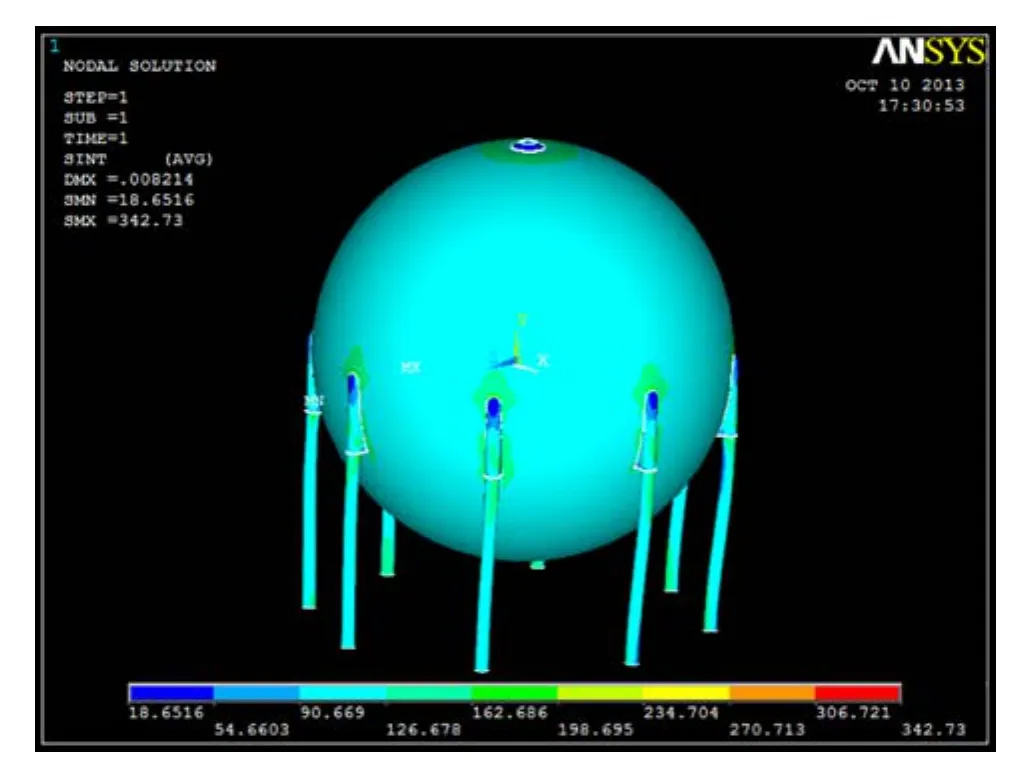
图5　应力强度云图

Ni=50000Nj=100000

Si=112.14Sj=91.30

按照GB50017-2003[3]附录C公式，可以计算得：

4.2疲劳寿命有限元计算

基于局部应力—应变法，对图5应力强度最大地方进行疲劳寿命分析[4].采用ANSYS软件后处理，录入表1的设计应力幅和对应的循环次数的疲劳特性，选取应力强度最大地方的节点，事件数为1，每一事件的载荷步为2.将载荷循环次数设为100 000，运算求解得到疲劳使用系数为1.906 72，循环次数为52 446次，将结果进行整理归纳，如表2所示.

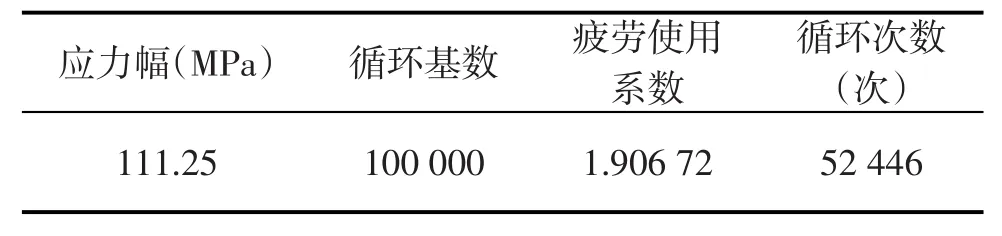
表2　球罐循环寿命有限元结果

疲劳寿命的有限元结果与经验计算结果比较如表3，表中的计算误差为2％，误差产生的原因是由于分析中没有考虑球罐腐蚀、应力集中等因素对疲劳寿命的影响[4].

5　结论

借助ANSYS软件后处理，计算球罐在两种工况下的疲劳寿命与根据公式计算出球罐疲劳寿命，两者基本一致.因此，采用ANSYS软件后处理，能有效解决疲劳分析问题，为进一步疲劳扩展寿命的计算奠定基础，弥补数值解法的不足.

表3　疲劳寿命计算结果比较

[1]赵石军.球罐支柱与球壳连接处局部应力分析[J].压力容器, 2000（17）：34-34.

[2]程光旭.压力容器低周疲劳寿命的损伤力学理论研究[J].西安交通大学学报,1994（11）：60-65.

[3]中华人民共和国建设部.GB50017-2003钢结构设计规范[S].北京：中国计划出版社,2003.

[4] 翁剑成.基于ANSYS软件的三通管疲劳寿命分析[J].化工设备与管道,2011（6）：46-47.

[5]全国压力容器标准化技术委员会.JB4732-95钢制压力容器－分析设计标准[S].北京：中国标准出版,1995.

[6]范钦珊.压力容器的应力分析与强度设计[M].北京：原子能出版社,1983.

（编校：许洁）

The Fatigue Life Analysisof the Steel Spherical Tank Based on Finite Element

WENG Jiancheng,XIEHuangsheng,LU Jianxiang,ZHANGXuehua
（Physicsand Mechanical Engineering Department,Longyan University,Longyan,Fujian 364012,China）

The S-N curve of the 16MnRmaterialswasestablished by using a common slope and the danger pointof stress amplitude were calculated with the ANSYS software.The steel spherical tank fatigue life was obtained respectively ac⁃cording to the analysis and design of the standard formula of steel pressure vessel and ANSYS post-processing.It pro⁃videsefficientcomputingmodel for calculating life in the industry.

S-N curve；fatigue lifeanalysis；finiteelementanalysis

TB

A

1671-5365（2015）06-0010-03

2014-11-20修回：2014-12-09

福建省教育厅B类项目“龙岩学院校立服务海西”（JB12219）；龙岩市先进机械设计制造公共服务平台建设资助项目（2012LY01）

翁剑成（1978-），男，讲师，硕士，研究方向为计算力学

网络出版时间：2014-12-10 09：16网络出版地址：http：//www.cnki.net/kcms/detail/51.1630.Z.20141210.0916.003.html

引用格式：翁剑成，谢煌生，卢建湘，等.钢制球罐疲劳寿命的有限元计算[J].宜宾学院学报,2015,15（6）：10-12.