随机波动模型贝叶斯估计效率研究
何永涛,王 飞
(南开大学a.数量经济研究所;b.经济学院,天津300071)
一、引 言
在金融领域中,金融时间序列大多表现出方差的“波动集群”特征和分布的“高峰厚尾”特征。为了刻画金融时间序列的这种特征,需要着重考察其方差过程的建模,这成为异方差时间序列模型发展的根本动因。目前,对于条件方差过程建模策略的研究主要有两类。一类是将条件方差作为因变量、将当前和过去数据平方值作为自变量的建模方法。这类方法起始于Engle提出的ARCH模型,随后由Bollerslev、Taylor、Nelson和 Cao、Tsai和 Chan、Andersen等扩展为一类广为熟知的GARCH模型族。另一类方法设定方差过程服从某一潜在随机过程,最早由Taylor提出,被称之为随机波动模型(stochastic volatility model,SV),主要应用于分析金融领域中期权定价问题[1]174-194。例如,Hull和White将随机波动模型应用于Black-Scholes期权定价公式,随后,Jacquier等、Harvey等以及Shepherd等系统地阐述了SV模型的建模策略与应用步骤,并由金融数学领域引入到计量经济学领域,标志着SV模型已经日臻成熟。SV模型的标准形式是:
上式中,yt为t时刻所持有资产的收益率,ht为t时刻收益率的对数波动水平。随机干扰项εt和ηt满足独立同分布条件E(εtεt+l)=0和E(ηtηt+l)=0,l≠0,且它们之间互不相关,即同时满足E(εtηt+k)=0,k≠0。参数|φ|被假定为|φ|<1,以保证ht的平稳性。考虑到参数的过度识别问题,SV模型的基本形式中设定参数β=1或者μ=0。由于ht真实数据生成过程是平稳随机过程,因此收益率yt是时变的且以某种方式进行聚集,从而有效地刻画了yt序列的“波动集群”特征。
与ARCH类模型相比,SV模型在金融数据及宏观经济序列建模应用中具有三个独有的优势:第一,由于yt服从混合分布,SV模型能够反映出金融序列中的“高峰厚尾”特征;第二,放松随机干扰项εt和ηt互不相关假定,SV模型能够更直接地刻画金融序列中的“非对称性”特征;第三,同等拟合效果下,SV模型所需估计的参数更少。基于以上优势,SV模型在金融领域建模中的应用日趋广泛。
在SV模型的建模过程中,模型的参数估计是最为关键的一环。考虑到SV模型的似然函数是无解析解的多重积分形式,传统的极大似然估计方法不能直接使用,SV模型的参数估计通常采用广义矩估计方法、伪极大似然估计方法和贝叶斯估计方法。广义矩估计方法最早由Melino和Turnbull提出,并由Jacquier等、Anderson和Srensen等引入SV模型进行发展完善[2]。其优点在于不需要正态分布假设且允许误差项存在异方差和序列相关,但该方法的有限样本性质较差,对于波动持续性参数φ接近于1的参数值,其收敛于无条件矩的速度相当缓慢,大体上是一种相当无效的方法。伪极大似然估计方法由Harvey等提出[3]。该方法假定εt服从正态分布,通过将标准SV模型变换成状态空间形式,并利用Kalman滤波构造预测误差项的似然函数,然后使用数值优化方法(EM算法、Newton-Raphson算法等)进行迭代。其优点在于它提供了波动性序列ht的预测值、滤波值和平滑值,方便扩展到更一般的模型,但是估计量不具有有效性,对于方差系数τ较小时,其有效性迅速恶化。
近年来,多数研究者采用贝叶斯估计方法来完成SV模型的估计。在贝叶斯估计方法框架下,SV模型的参数和潜在波动过程都被当作随机变量处理,通过计算参数的边缘后验分布来完成贝叶斯推断,但在大多数情况下参数和变量的联合分布是非常复杂的高维分布,因此不能直接从这个分布中抽取样本。马尔科夫链蒙特卡罗(Markov chain-Monte Carlo,MCMC)技术为我们提供了有效的解决办法。MCMC技术可以间接地从参数的联合分布中生成随机样本,而不必直接设定分布的具体形式,只要样本容量足够多,就可以得到收敛到真实值的样本统计量。目前,MCMC技术被认为是处理这种困难问题的最有力、最有用途的工具。
对于建模过程中SV模型的贝叶斯估计效率问题,尚未发现有文献做过深入研究。在实际建模应用中,研究者通常采用不同MCMC抽样方案来确定SV模型的估计值,但其适用性如何,是否对不同样本量和抽样次数具有稳健性等问题,已有文献均未做过相关研究。本文将选取四个具有代表性的MCMC抽样方案,从算法耗时、抽样效率和估计精度三个方面对此进行研究。
二、SV模型的MCMC抽样方案
由于Taylor提出的SV模型假定过于苛刻,为了满足实际的需要,众多研究者对其进行了扩展,扩展形式主要有厚尾SV模型、非线性SV模型、长记忆SV模型、非对称SV模型、多元SV模型和多因子SV模型等。尽管SV模型存在众多扩展形式,但是通过将MCMC算法进行扩展可以很容易地处理其参数的估计问题。
为了建立SV模型的MCMC抽样方案,需要重新考察SV模型中的待估计参数。由式(1)和式(2)可知,如果给定不可观测波动性序列ht初始值h0以及未知参数τ2和θ=(μ,φ)′的先验分布,那么未知参数(θ,τ2)的条件后验分布可由如下贝叶斯法则求取:

其中,h和y 分别代表列向量(h1,h2,…,hn)′和(y1,y2,…,yn)′,p(h0)、p(θ)和p(τ2)是已给定的未知参数h0、θ和τ2的先验分布。注意到,利用式(3)仅能得到未知参数θ和τ2的条件后验分布,然而由于SV模型中波动性序列ht也是不可观测的,因此需要进一步对ht的条件后验分布进行考察。同样,ht条件后验分布和联合后验分布可由贝叶斯法则求取:

上式中,h-t表 示 抛 除t 期 后ht的 列 向 量 (h0:(t-1),h(t+1):n)′。理论上,结合式(3)和式(4)即可得到SV模型中所有未知参数的事后估计值,但实际上由于上述后验分布为复杂的高维分布,无法直接求取解析解,通常使用MCMC技术来解决此类问题。MCMC方法首先建立一个马尔科夫链,使得上述后验分布为其平稳分布,然后运行此马氏链充分长时间直至收敛到平稳分布。建立此类马氏链的方法包括 Metropolis算法,Metropolis-Hastings(MH)算法和Gibbs算法。
(一)随机游走Metropolis抽样方法
随机游走Metropolis抽样方法最早由Jacquier等引入到SV模型的贝叶斯估计中,该方法由“回归参数”和“波动状态变量”两个抽样模块构成[4]。“回归参数”抽样模块用于完成上述式(3)中未知参数θ和τ2的条件后验分布p(θ,τ2|h,y)的抽样;“波动状态变量”抽样模块用于完成上述式(4)中波动性序列ht的条件后验分布的抽样。
在实现“回归参数”抽样模块时,Jacquier等为未知回归参数θ和τ2设定正态—逆伽马类型的先验分布。由于正态—逆伽马先验分布与后验分布构成共轭分布,因此参数θ和τ2的条件后验分布同样是正态—逆伽马类型的分布。具体来说,假定先验分布的具体形式为,则其条件后验分布为。其中条件后验分布的参数和与先验分布的超参数和之间存在如下关系:

状态变量h抽样问题由“波动状态变量”抽样模块来完成。具体来说,设定ht初始值h0的先验分布为正态分布,则其条件后验分布为。其中参数 mt和C2t与先验分布的超参数m0和C0之间存在如下关系:

利用上述结果可以实现ht的条件后验分布的抽样,结合式(4)的结论,可以构建出ht的条件后验分布的表达式:

上式中,给定合适的调整方差v2h,则波动状态变量ht的条件后验分布可由随机游走Metropolis抽样方法实现。具体步骤如下:
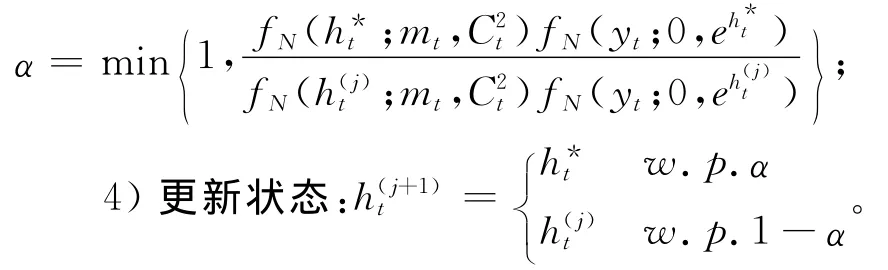
重复上述过程,直至马氏链收敛到平稳分布。需要说明的是,随机游走Metropolis抽样方法下得到的马氏链,其收敛性对v2h选择比较敏感。如果v2h取值过大,多数的候选点将被拒绝,此时算法的效率很低。相反,如果v2h取值过小,则候选点几乎都被接受,此时所得的马氏链几乎是纯随机游走过程,这同样也是一种低效率。Robert等建议v2h的取值应使得接受率α∈ [0.5,0.85],这样才可以保证得到的链有较好的性质。
(二)独立 Metropolis-Hastings抽样方法
独立Metropolis-Hastings抽样方法是 MH算法的特殊情形,最早由Kim等引入到SV模型的分析之中[5]。独立 Metropolis-Hastings抽样方法与随机游走Metropolis抽样方法实现方法大致相同,主要的区别是在“波动状态变量”抽样模块中使用独立MH抽样代替随机游走Metropolis抽样。具体来说,Kim等研究发现式(9)中p(yt|ht)的对数形式具有如下性质:
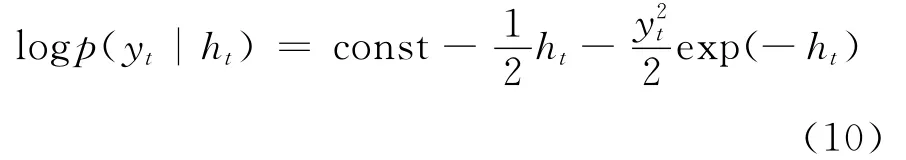
上式中,const表示某一常数,利用泰勒公式将幂指数项exp(-ht)在mt附近进行一阶展开,则:

从而可以得到ht分布函数的一个近似形式
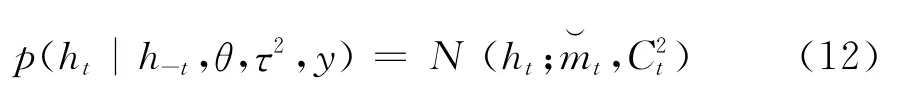
3)计算ht*被接受的概率:

独立 Metropolis-Hastings抽样方法的优点是容易实施,而且在提议分布和目标分布很接近时也趋于表现良好,但是当提议分布和目标分布差别较大时,其表现就较差。
(三)正态近似和FFBS抽样方法
上述两种方法中,波动状态变量ht都是由逐期抽样而获得,因而被称之为“逐分量”抽样。“逐分量”抽样在波动序列ht之间的相关程度较低的情形下表现良好,但是如果波动序列ht之间高度相关,将会产生抽样之间的高相关性,从而导致所建立的马氏链收敛于平稳分布的速度十分缓慢。为此,一些学者致力于研究对波动状态变量ht的“成块”抽样,将要讨论的方案Ⅲ和方案Ⅳ即是这类方法的典型代表。
在进行“成块”抽样之前,需将SV模型写成状态空间的表达形式,为此,首先对前文式(1)两边进行平方并取对数:

其中y*t=logy2t,ξt=logε2t。式(2)和式(13)构成了SV模型的状态空间形式。值得注意的是,上式中扰动项ξt不再服从正态分布,Abramowitz和Stegun研究发现[6]925-961,此时扰动项ξt的期望为E(ξt)=-1.27、方差为var(ξt)=π2/2。由于只有在状态空间模型扰动项服从正态分布时,才能使用Kalman滤波进行波动状态变量的更新,为此,Ruiz建议将扰动项ξt进行正态近似处理:ξt~N(β,σ2),β=-1.27、σ2=π2/2。设定zt=y*t-β,则上式(13)变换为:

其中υt~N(0,1),式(2)和式(14)构成了SV模型的正态状态空间形式,采用FFBS(Forward Filtering Backward Sample)从p(h|θ,τ2,σ2,z)中即可完成状态变量ht的“成块”更新。需要强调的是,采用正态分布对扰动项ξt的分布进行近似并不是一个理想的方案,它会在分布的尾部引入一个较大的偏差。
(四)有限混合分布近似和FFBS抽样方法
为了解决方案Ⅲ中由扰动项ξt正态近似引起的偏差问题,Kim等构造了由7个正态分布加权而成的混合分布,并证明采用混合分布对随机干扰项ξt的分布进行近似要比单纯的正态近似效果更好。构造混合分布的7个正态分布加权表达式为:
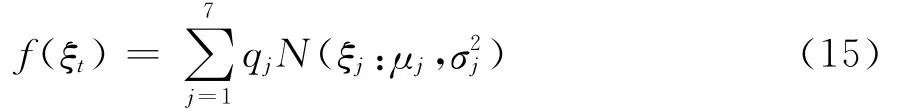
其中,μj、σ2j是第j个正态分布的均值和方差,qj是选择第j个正态分布概率,f(ξt)是正态分布的混合分布①① Kim等给定的7个正态分布的参数(qj,μj,σ2j 分别为:(0.0073,-10.12999,5.79596)、(0.10556,-3.97281,2.61369)、(0.00002, - 8.56686,5.1795)、 (0.04395,2.77786,0.16735)、 (0.34001,0.61942,0.64009)、 (0.24566,1.79518,0.34023)、(0.25750,-1.08819,1.26261)。。与正态分布近似相比,有限混合正态近似拟合效果更好。进一步,通过引入指示变量Ω{I1,I2,…,In}使得f(ξt|It)满足f(ξt|It)~N(μj,σ2j),p(It=j)=qj。这种表示的优势在于可以直接从离散分布p(It=j)中抽取It,进而基于式(13)可以直接采用FFBS抽样方法对波动状态变量h进行“成块”抽样。
需要说明的是,抽样方案Ⅳ与抽样方案Ⅲ的抽样过程是一致的,主要的变化是在抽样方案Ⅳ中,使用有限混合分布替代正态分布来近似扰动项ξt的分布。正如上文所述,有限混合分布对扰动项ξt分布的近似效果与正态分布相比具有较大改善,但同时也注意到,由于有限混合分布每次需要从7个正态分布中抽取样本,因此将在一定程度上增加运算的负担,从而影响抽样的速度。
三、评价准则
上述四种抽样方案分别建立了四种不同的MCMC抽样方案来完成SV模型的贝叶斯估计,不同抽样方案所建立的马氏链也不同。实质上,MCMC抽样方案优劣关键在于建立的马氏链的性质。依据遍历均值定理,一个好的链应该具有快速混合性质,即从任意位置出发都能很快收敛到平稳分布。基于此,我们从算法耗时、抽样效率和估计精度三个方面建立对四种抽样方案的评价准则。
算法耗时用于衡量算法的时间复杂度。随着计算机的普及和性能的提高,MCMC抽样方案对抽样速度的要求已经得到很大改善,但是在分析大数据时,运算速度仍是衡量抽样方案优劣的一个重要指标。考虑到不同配置的计算机在数据处理速度上存在较大差别,为了保证比较的公平性,我们在同一硬件平台上完成对四种方案进行分析。具体的运行平台配置为Intel Core 2T5870 2.00GHZ,2GRAM。
抽样效率用于衡量马氏链的收敛速度。影响抽取样本无效率的一个重要因素是马氏链收敛性,通常检查马氏链收敛与否的最直接方法是轨迹图和自相关图。轨迹图适用于自相关水平较弱时马氏链的收敛性检查,如果自相关水平很高,轨迹图诊断马氏链收敛性的效果就比较差。与轨迹图相比,自相关图的适用性更广一些,这主要是因为自相关函数随着步长的增大而减小较快。考虑到现实模型中大多参数存在自相关而使得抽样走遍整个目标分布的速度比较慢,因而自相关图更适合检查马氏链的收敛性。但是,如果在目标分布的一个局部支撑上产生的值的方差非常小,将导致单独一个马氏链看起来已经收敛而实际上在整个支撑上并未达到收敛,此时自相关图也同样失效。为此,构造如下无效率因子:
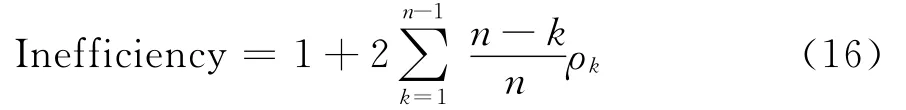
其中ρk为滞后k期的自相关函数。通过计算无效率因子,我们基于从不同初始值出发,然后检查几个平行的初始值非常分散的马氏链,发现收敛很慢的效率就会高得多。
估计精度用于衡量估计结果的有效性,使用MC误差统计量来进行衡量。MC误差监视了由随机模拟而带来的波动性,精度高的估计量,其MC误差必须很小且精度随着样本容量递增。Gelman和Rubin提出使用多层链式迭代来计算MC误差,具体来讲,假设由k个马氏链,每个链有m个样本,在目标分布下其期望为φ和方差为δ2。使用fij表示第i个链的j个样本的MC值,那么在混合样本中,φ的一个无偏估计为,而链间的方差B/m和链内的方差W 分别为:
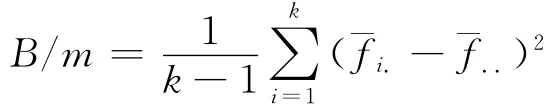
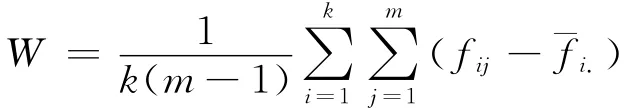
从而可以使用B和W 的加权进行估计δ2:

四、模拟分析
(一)数据生成过程
已有文献研究表明,如果φ接近于1且τ2较小,那么波动ht存在高度相关性,此时,如果所建立的马氏链不合理,就会产生抽样之间的高度相关性,将导致抽样算法的无效率,最适合用于算法优劣的评价。因此,我们设定生成模拟数据的真实参数值分别为h0= 0.0,μ =- 0.00645,φ = 0.99,τ2= (0.0225,0.45)。依据式(2),则ht(t=1,2,…,n)由生成,其中ζ从正态分布N(0,0.15)中随机生成。利用ht并结合式(1),从而yt可从正态分布中生成。考虑到样本容量可能带来的影响,分别使用n=100和n=500两种情形进行研究。
在运行MCMC估计方法之前,还需考虑先验分布的设定。首先设定参数(θ,τ2)的共轭先验分布为正态—逆伽马分布:

(二)模拟结果分析
所有的运算结果都通过R(Version3.0.2)软件来完成。首先,采用上述设定生成模拟数据,然后分别使用第二节中的四种抽样方案来完成对未知参数的贝叶斯推断。为了评价各抽样方案的优劣,我们在抽样过程中分别计算出抽样算法的算法耗时、无效率因子和MC误差三个评价指标。
由表1中各抽样算法的运算耗时可知,方案Ⅳ所需算法耗时最长,方案Ⅰ次之,方案Ⅱ和Ⅲ差别较小且相对较短。这说明,在对波动变量进行抽样时,“逐分量”抽样算法与“成块”抽样算法在算法耗时方面几乎无异;各方案之间算法耗时的差异大部分源于对随机干扰项ξt近似方法处理方式的不同。

表1 算法耗时表(单位:秒)
在分析算法的收敛性问题时,我们参照Reis的做法,重点考察波动序列ht的第100期的样本收敛性质[7]。图1给出了不同(τ2,n)组合下四种抽样方案的样本自相关函数。由图1可知,当(τ2,n)的取值为(0.0225,100)时,四种抽样方案下波动变量h100自相关函数衰减均非常缓慢,但是随着τ2和n取值变大,方案Ⅲ和Ⅳ以极快的速度衰减至0附近,并且保持在较低的相关性水平状态,方案Ⅱ次之,方案Ⅰ衰减速度最慢。这主要是因为数据生成过程中φ的取值接近于1,导致波动变量之间相关性较高,结果“逐分量”抽样算法就会产生抽样之间的高相关性,从而使得h100自相关函数衰减缓慢,而“成块”抽样算法将所有波动变量作为一个整体进行抽样,因此能够使得样本自相关函数具有较快的衰减速度。
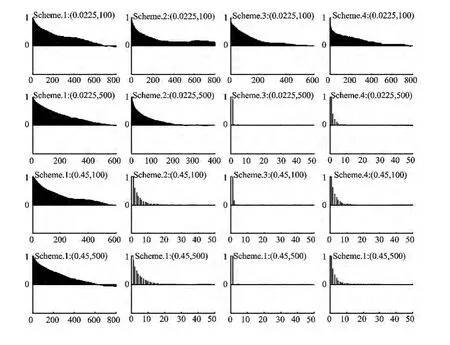
图1 状态变量h100的样本自相关图
考虑到可能会出现的局部收敛而整体未收敛情况,我们为随机数发生器设定不同种子,再次对四种抽样方案重复进行50次模拟,每次模拟2 000次并计算四种情形下的各参数的无效率因子。由表2中各参数无效率因子的计算结果可知,总体上,随着τ2和n取值变大,四种抽样方案的无效率因子取值均变小,说明抽样效率在逐步提高,而且在四种情形下,方案Ⅰ中各参数的无效率因子值均远大于其它三种方案,这验证了方案Ⅰ在四种方案中自相关函数衰减最慢的事实。
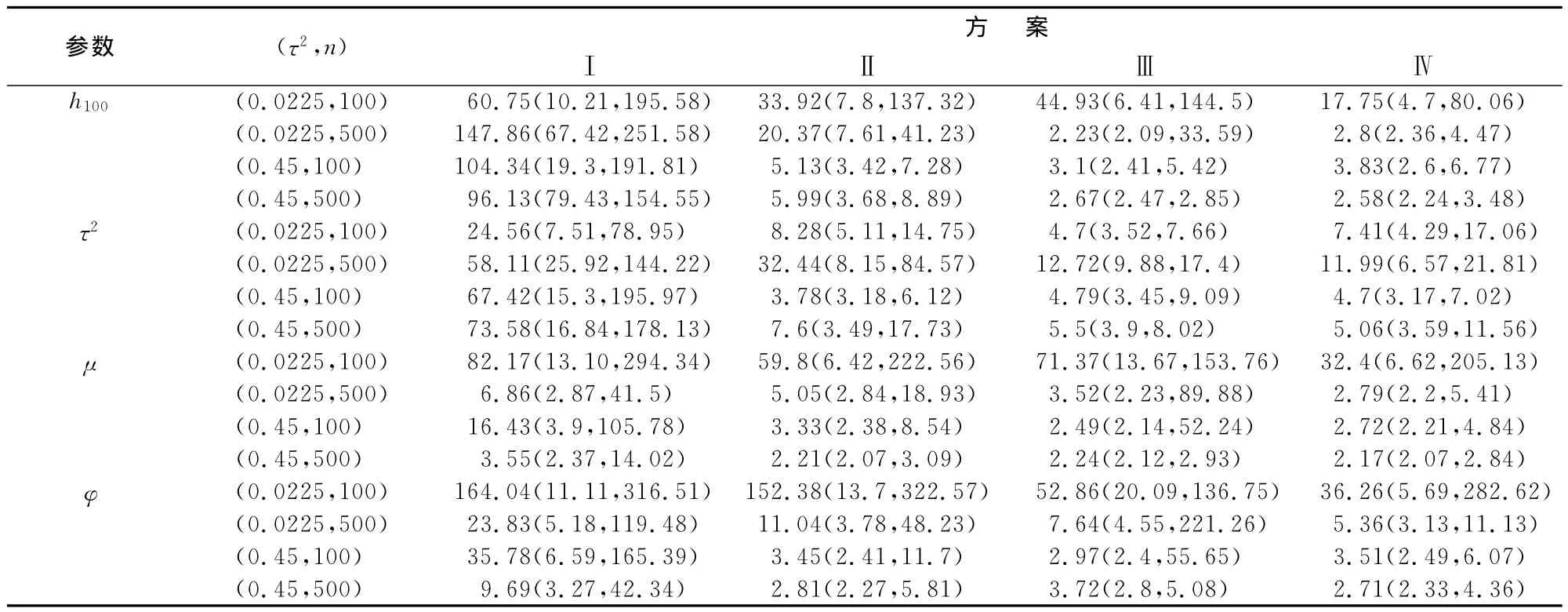
表2 各参数无效率因子的中位数、5%分位数和95%分位数表
为了评价各抽样方案下估计量的估计精度问题,根据所得到的抽样样本,我们首先绘制出各参数后验核密度分布图,以便直观掌握各个参数的后验分布情况。图2给出了四种抽样方案下各参数在不同情形时的后验核密度分布图。
由图2可知,在四种情形下,方案Ⅱ和方案Ⅳ下各参数的后验分布都较为近似,方案Ⅰ和方案Ⅲ则与前两者差异较大,方案Ⅰ的差异主要表现在各参数的后验分布有时会呈现明显的双峰特征,而方案Ⅲ的差异则主要表现在各参数后验分布的偏度和峰度方面。例如,当(τ2,n)的取值为(0.0225,500)和(0.45,100)时,在抽样方案Ⅲ下参数φ和τ2的后验分布均出现偏度和峰度的偏差。同时,当(τ2,n)的取值为(0.0225,100)时,在抽样方案Ⅲ下参数φ的后验分布表现出更明显的双峰特征。这种现象出现的主要原因是,方案Ⅰ下参数的自相关函数衰减较慢导致马尔科夫链尚未收敛,而对于方案Ⅲ下各参数的后验分布差异则是由于在抽样过程中该方案使用了正态分布来近似随机干扰项的分布,从而导致在抽样过程中存在较大偏差。这两种情况都会使得在进行贝叶斯推断时产生一定的偏差。

图2 各参数后验分布的核密度图
进一步,表3中给出了四种方案下SV模型中各参数的相关统计量,包括均值、绝对误差和MC误差与标准差的比值。我们预期方案Ⅱ和方案Ⅳ下各参数均值应该较为近似,从结果来看,在n=100,500以及不同的τ2值下,方案Ⅱ和方案Ⅳ下各参数的均值确实较为接近,这与预期相符合。同时可以看出,在不同的情形下,方案Ⅲ与它们差异均较大。通过绝对误差可以看出,在n=100,500情况下,随着τ2取值变大,参数h100的绝对误差也随着变大。这说明波动系数增大会干扰模型的估计结果。另外,MC误差与标准差的比值都远小于1,说明MC误差要远小于样本标准差,预示着参数的马尔科夫链比较平稳。
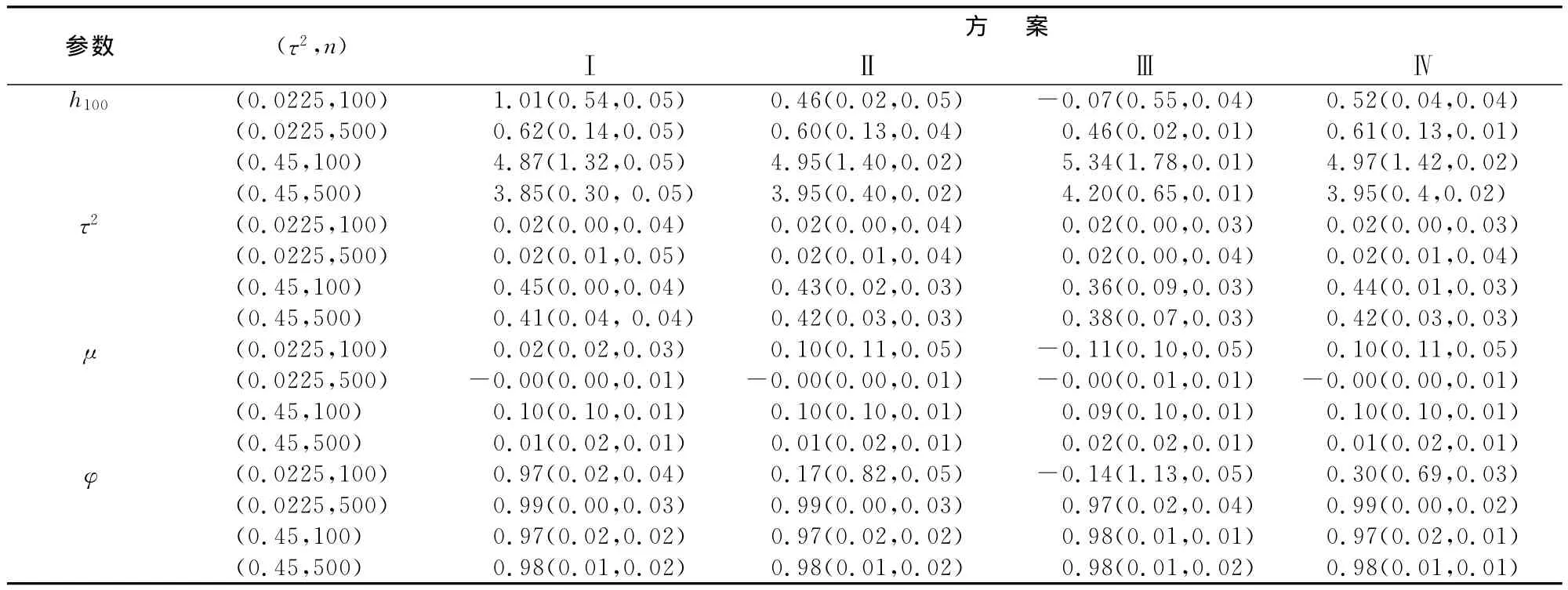
表3 参数的均值、绝对误差和MC误差与标准差比值表
最后,综合以上模拟分析的结论,对四种抽样方案的表现进行排序。为了能更直接地评价不同情况下四种抽样方案的优劣,我们分别在每种情况下对它们排序,并统计它们在每个次序中出现的次数,表4给出了次数的累计百分比。
表4中的结果显示,单纯从四种方案的抽样效率方面而言,抽样方案Ⅳ在次序1和2中占据绝对优势,累计百分比分别为62.5%和93.75%;抽样方案Ⅲ次之,累计百分比分别为37.5%和75%;抽样方案Ⅱ和抽样方案Ⅰ在抽样效率方面相对较差,其中抽样方案Ⅱ在次序1和2中的累计占比分别为0%和31.25%,而抽样方案Ⅰ则从未在次序1和2中出现。这表明,本文提到的四种抽样方案中,“成块”抽样具有更高的抽样效率,具体的抽样效率由高至低分别为方案Ⅳ、方案Ⅲ、方案Ⅱ和方案Ⅰ。对于四种方案的估计精度而言,在次序1中四种抽样方案的占比基本保持稳定,而在次序2中则发生较大的变化,其中抽样方案Ⅳ的累计占比增加幅度最大,为68.5%;其次是抽样方案Ⅱ,在次序2中其累计占比增加至62.5%;相对而言,抽样方案Ⅰ和Ⅲ的增加幅度较小。如果以次序1和2中的累计占比来衡量抽样方案的估计精度,那么四种方案中方案Ⅳ最优,其次为方案Ⅱ、方案Ⅰ和方案Ⅲ。

表4 次数的累计百分比表
五、结 论
本文系统地总结了随机波动模型的建模进展,对近年来随机波动模型的几种主要估计方法进行了评述,并分析了它们各自的优势和不足。重点讨论了贝叶斯估计方法下随机波动模型的MCMC抽样算法,通过模拟分析得出以下几个结论:
第一,在算法耗时方面,有限混合分布近似和FFBS抽样方法算法耗时最长,独立 Metropolis-Hastings抽样方法次之,其它两种方法较短且差别较小。
第二,通过观测各参数的样本自相关图,可知两种“逐分量”MCMC抽样方法中各参数的自相关图衰减缓慢,而两种“成块”MCMC抽样方法中各参数的样本自相关图以极快的速度衰减至0附近,并且保持较低的相关性水平。
第三,通过对比四种方案中各参数的估计值与真实值之间的绝对误差,结果表明基于有限混合分布近似的“成块”抽样算法在估计精度方面均优于其它三种方法。
需要说明的是,在实际应用中,究竟采用何种抽样方法来完成随机波动模型的贝叶斯估计,取决于研究者的研究目的,本文只是提供一个可供选择的依据。
[1] Taylor J.Modeling Financial Time Series[M].New York:Wiley,1986.
[2] Anderson G,Srensen E.GMM Estimation of a Stochastic Volatility Model:a Monte Carlo Study[J].Journal of Business and Economic Statistics,1997(14).
[3] Harvey A,Ruiz E,Shephard N.Multivariate Stochastic Variance Model[J].Review of Economic Studies,1994(61).
[4] Jacquier E,Polson N,Rossi E.Bayesian Analysis of Stochastic Volatility Models[J].Journal of Business and Economic Statistics,1994(12).
[5] Kim S,Shephard N,Chib S.Stochastic Volatility:Likelihood Inference and Comparison with ARCH Models[J].Review of Economic Studies,1998(65).
[6] Abramowitz M,Stegun N C.Handbook of Mathematical Functions[M].New York:Dover Publications Inc,1970.
[7] Reis A,Salazar E,Gamerman D.Comparison of Sampling Schemes for Dynamic Linear Models[J].International Statistical Review,2006(74).

