大数据挖掘的均匀抽样设计及数值分析

李 毅，米子川

（山西财经大学 统计学院，山西 太原030006）

一、引 言

随着社交媒体、手机APP、安全监视器、天文望远镜、卫星、工业生产线和各种传感器等基于互联网的硬件和应用软件的普及，来自不同过程的统计数据不断产生，其物理特征包含文字、图像、音频、纯数据等等，这些数据数量庞大、结构复杂且维度多样［1－4］。面向大数据的统计分析，存在三个方面的困难和挑战：首先，由于大数据的背景分布缺乏先验信息，大多数分析过程是从单纯的数据出发，这种分析过程被称为“冷启动”。通常大数据的产生和收集在事先并没有特别的目的，或者收集者的目的并不明确，因此无法获得显著的先验分布信息。与此相反，在传统的统计数据采集方法中，实验设计则是一个目的明确的数据搜集过程，即在一定的控制变量和区组条件下完成对数据的重复测度和记录。实验设计所得的资料是通过事先科学设计的，Fisher提出的原则是“均衡分散，整齐可比”，说明实验设计记录的数据是一种结构完整、信息充分的“小数据”；其次，就资料收集目的而言，大数据收集的目的也是不同的，其收集过程和目的并非统计分析的目的，但对于价值的提取二者是相同的，并在大数据的分析过程中，希望从数据中发现一些有趣的特征或模式，藉此提供有价值的信息以供决策参考；第三，大数据的规模显著地大于传统的统计数据，但是所蕴涵的信息量则相对稀少，一般被称为数据的“稀疏性”。根据统计学基本理论，有用的样本量应该是越多越好，但是大数据的信息贡献却不是这样，数据量大不一定意味着有价值的信息就会增多，大量的虚假知识甚至会损害数据信息，因此“大数据等于总体”的思想是错误的。此外，大数据建模时，数据本身的属性也会成为统计建模和分析的难题，如高维度、时间序列特性、变量间的复杂关系等等，都是亟待解决的问题。事实上，对于较小的数据集，上述问题可能不存在困扰，但对于大数据则可能就是一个严重的问题。所以，如何从大数据中汲取有价值的信息是统计学面临的一项重要挑战。

从统计学角度看，面对大数据分析中的上述问题，随机抽样仍然是最直接的解决方法，可以利用抽样技术从相同数据结构的大数据集中获得相对小的随机样本。必须指出的是，抽样并不能告诉人们有用的信息在哪里，而是加速找到有用特征的工具。本文的主要思想是：在大数据总体的参数估计和统计推断问题中，为了节约计算成本，笔者希望尽可能减少样本的数据量，且同时应得到一个良好的响应曲面来描述复杂的大数据结构，均匀设计便是达到上述目标的一个有效方法，该方法是中国数学家方开泰教授和王元教授于1980年首次提出，主要目的是在定义域上寻找均匀布点。大量相关文献证实利用均匀设计来选取输入值，不管因变量与自变量之间存在何种的关系，所得到的资料对于基础模型通常都具有良好的描述和再现能力。30多年来，已有大量的均匀设计理论研究和实证分析案例在工农业生产和科学实践中得到了展现［5］［6］131－170［7－12］。

本文采用预测抽样的思路展开探索［12］，通过均匀设计的基本原理进行均匀抽样，即利用机器学习中监督式学习的概念，把被抽中的样本点作为机器学习中的训练集，使其尽量充满原始大数据集的全部空间，以便能真实反应大数据的结构，进而训练得到一个最优模型（这个模型属于某个函数的集合，最优则表示在某个评价准则下是最佳的），最后通过测试集的误差率来讨论均匀抽样的有效性［13］。

二、均匀抽样方法

（一）均匀性度量

其中V（f）是函数f在定义域C上的总变差，若函数f平稳，V（f）则偏小，反之亦然；D （Tn）为集合Tn在定义域C上的偏差，即度量集合Tn均匀性的测度，如果D （Tn）越小，则集合Tn散布性越均匀。

均匀性度量的定义方法有多种，使用范围最广的方法为偏差法［15］。假设x为定义域C中一个n个点的集合，则定义p在定义域C偏差为：

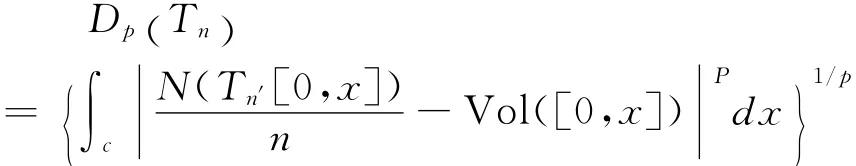
当采用偏差法为准则来做均匀设计时，定义域的原点明显扮演着很特殊的角色。事实上，若从不同的角度看待定义域（Cs）中的布点均匀性，每个顶点的重要性应该是一样的。马长兴在使用偏差做均匀设计的准则时所找出的布点会产生方向性，用对称偏差则可以修正这项缺失［16］。F．J．Hickernell提出的中心化L2－偏差同样可以修正偏差具有方向性的缺点，此测量的优点是同时把分布在高维度上的点集合投影到低维度的坐标子空间上来做均匀性的判断［17］。另外，中心化L2－偏差也不会因为坐标旋转而改变，所以中心化L2－偏差是目前被广泛应用并证明有效的均匀性测量方法［5］。

公式（1）中定义域C＝ ［0，1 ］k，其中k代表立方体的维度。举例来说，k＝2表示单位正方形，k＝3则表示单位正六面体，而均匀设计主要的目的便是在此定义域中寻求均匀的布点方式，在定义域C中抽样，则收敛速度为 O（n－1（logn ）k），而随机抽样收敛速度为O（n－1／2（loglogn）1／2）。

式（1）中函数f为希望估计的模型，一般要求f对任何函数都成立。根据f （xi），i＝1，2，…，n 的值，利用均匀抽样的数据做监督式学习，这个过程符合统计学中关于大数定律的基本思想，即当试验次数足够多时，事件出现的频率f （xi）无穷接近于该事件发生的概率函数f，进而可以利用式（1）的Tn求函数f。

（二）均匀抽样算法的构造

求均匀性是一个优化问题，由于求解是在一个离散的空间上，目标函数的连续性和可微性已失去意义，从而传统的各种优化方法失去了效用。为此，本文设计了利用门限接受的启发式算法进行均匀抽样。

设S为全部的大数据集合，抽样步骤如下：

步骤1：设置初始值。设置初始门限值T＞0，先从S中随机抽取n0个点，记为，令，计算的值。

步骤2：产生新的样本。从S中读取下一轮数据，记 为，将z看作，计算的值。

步骤3：产生新解。计算，若δ＜T，则z就被选中，而将其置入中S的集合，设n＝n＋1，并返回步骤2。

步骤4：判断是否满足终止条件。若满足S中的点被读取完，则抽样结束。

对于控制参数，即门限值T，循环算法持续进行“产生新解—判断—接受或舍弃”的迭代过程，当T较大时，抽样所产生的样本量较低，进行的是粗略随机搜索。随着T的逐渐降低，抽样所得的样本量越来越高时，进行的是精细检索。

三、数值分析

（一）模拟数据的抽样过程

采用R语言随机模拟了一组二维数据X2000×2＝（X1，X2），其中两个分量X1、X2相互独立，其散点图见图1所示。

图1 二维模拟数据X2000×2图

利用均匀抽样从模拟数据进行抽取，获得了一个样本量为369的随机均匀样本，如图2所示。

从图1与图2结果来看，抽出的均匀结果为，说明采用中心化L2－偏差的CD2进行抽样的效果不错，达到了预期的效果，即尽可能减少样本量，且同时得到一个良好的响应曲面来描述和逼近复杂的大数据结构。

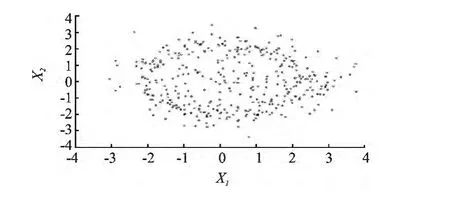
图2 二维模拟数据X2000×2均匀抽样图

（二）胎心宫缩监护数据的均匀抽样实证分析

本文的原始数据选取吴喜之教授提供的胎心宫缩监护数据，一共包括2 129个观察值及23个变量。吴喜之教授使用了前22个变量作为自变量来预测因变量NSP（胎儿状态分类代码）的类别［18］56－70。笔者利用均匀抽样与随机抽样的样本作为训练集，其余样本为测试集，还采用了五折交叉的算法，应用到决策树（分类树）、adaboosting、bagging和随机森林算法中，分析结果见表1。

表1 四种数据挖掘方法不同抽样结果表

从表1中的测试集误差率可以看出，四种数据挖掘方法中均匀抽样的误差率最小、五折交叉次之、随机抽样最大，显然均匀抽样技术在四种算法模型中的表现均优于其他方法。

四、小 结

与传统的统计分析思想相比，大数据分析有着结构复杂、数据量大、信息稀疏杂乱等特点。因此，目前大数据分析初步形成了两个相对重要的研究方向：第一个方向是侧重数据的预处理，主要有采集、加工、分类和描述等，这个方向更多的文献和研究成果集中在信息处理和计算机科学领域；第二个方向是研究数据的统计规律，比如数据结构、关联和趋势分析等，这个方向主要是统计学、管理学、经济学和营销等领域的研究成果。目前，更多学者认为两者是一个整体，分析方法必须和数据预处理相匹配，大数据分析必须从数据的预处理开始，直至达成分析目的，这也是本研究的基本出发点。

本文尝试提出在大数据分析中继续使用抽样技术的观念，并通过均匀抽样方法的设计在机器学习中开展应用研究，即利用均匀设计的原理，将中心化L2－偏差的CD2和门限接受的启发式算法相结合进行抽样。本文提出的均匀抽样的概念和方法设计，在大数据典型储存方式数据库中可以得到较好的应用，特别是对需要减少计算量却又不知如何抽样的问题。与传统抽样概念不同的是在数据分析上，笔者主要先选取训练样本进行各项分析以测试样本检视结果，并在选取训练样本时发现均匀设计可以在样本均匀度、代表性等方面优于随机抽样，此结果可提供数据库抽样上更反映总体的数据进行后续分析，这一结论能为大型数据库中抽样数据在数据挖掘方法的应用提供参考，还能为大数据背景下的随机抽样技术的研究和发展提供佐证。

［1］ Jordan J M，Lin Dennis K J．Statistics for Big Data：Are Statisticians Ready for Big Data［J］．International Chinese Statistical Association Bulletin，2014，26（1）．

［2］ Fan J Q，Han F，Liu H．Challenges of Big Data Analysis［J］．National Science Review，2014，1（12）．

［3］ 乔晗．“大数据”背景下利用扫描数据编制中国CPI问题的研究［J］．统计与信息论坛，2014（2）．

［4］ Li R Z，Lin Dennis K J，Li Bing．Statistical Inference on Massive Data Sets［J］．Applied Stochastic Models in Business and Industry，2013，29（5）．

［5］ Fang K T，Lin Dennis K J．Winker P，Zhang Y．Uniform Design：Theory and Application［J］．Technometrics，2000，42（3）．

［6］ Fang K T，Lin Dennis K J．Uniform Experimental Design and Its Applications in Industry，Hndbook of Statistics in Industry［M］．New York：Eisevier，2003．

［7］ Li R Z，Lin Dennis K J，Chen Y．Uniform Design：Design，Analysis and Its Application［J］．International Journal of Materials and Product Technology，2004，20（1）．

［8］ Huang C M，Lee Y J，Lin Dennis K J，Huang S Y．Model Selection for Support Vector Machines Via Uniform Design［J］．Computational Statistics ＆ Data Analysis，2007，52（1）．

［9］ 张维群．均匀设计在多指标抽样调查方案设计中的应用［J］．统计与信息论坛，2009（10）．

［10］Yang J F，Sun F S，Lin Dennis K J，Liu Min－Qian．A Study on Design Uniformity Under Errors in the Level Values［J］．Statistics and Probability Letters，2010，80（19）．

［11］Jeong I J，Kim K J，Lin Dennis K J．Bayesian Analysis for Weighted Mean－squared Error in Dual Response Surface Optimization［J］．Quality and Reliability Engineering International，2010，26（5）．

［12］Tang Yu，Xu H Q，Lin，Dennis K J．Uniform Fractional Factorial Designs［J］．The Annals of Statistics，2012，40（2）．

［13］Chao M T．On CRIS－DM and Predictive Samping［J］．Journal of the Chinese Statistical Association，2002，40（4）．

［14］Brandolini L，Colzani L，Gigante G，Travaglini G．On the Koksma－Hlawka Inequality［J］．Journal of Complexity，2013，29（2）．

［15］Hickernell F J，Liu M Q，Yan C Y．Discrepancy Measures of Uniformiey［J］．Journal of the Chinese Statistical Association，2000，38（4）．

［16］马长兴．均匀性的一个新的度量准则—对称偏差［J］．南开大学学报：自然科学报，，1997，30（1）．

［17］Hickernell F J．A Generalized Discrepancy and Quadrature Error Bound［J］．Mathematics of Computation，1998，67（221）．

［18］吴喜之．复杂数据统计方法——基于R的应用［M］．北京：中国人民大学出版社，2012．