5A03铝合金管轴向压缩失稳形式及影响因素分析

李翀，鄂大辛，佘彩凤

（北京理工大学材料学院，北京 100081）

管材作为一种轻质吸能型材，容易实现产品的轻量化和强韧化，同时兼具低能耗、高功效等优异性能，因此不仅在压力管道和流体输送工程中得到大量应用，近年来也作为强化缓冲及轻量化构件等，广泛用于航空航天、汽车等工业中［1］。金属管材在弯曲成形和作为支撑构件的服役过程中，通常将承受或局部承受轴向压力，因此研究其轴向压缩问题具有重要的工程实用价值［2—4］。从20世纪60年代开始，许多的学者对管材轴向压缩变形的影响因素进行了实验和有限元研究以及理论分析［5—11］。已有报道大多是针对冲击载荷下管材的轴向压缩问题，对于准静态条件下短管轴向压缩的研究极少。文中在通过大量管材准静态轴向拉伸实验及有限元模拟研究管材受拉变形的力学性能的同时［12—16］，针对h0＜3d0的5A03短管轴向压缩进行了实验与有限元分析，为管材轴向压缩的力学行为及弯曲起皱等研究提供参考。

1 材料性质及实验方案

实验材料为航空航天用冷拔5A03铝合金（Al-Mg系防锈铝）管材，原始外径d0=14 mm，壁厚t0=1 mm，拉伸试样标距长度l0=100 mm，压缩试样高度h0=14 mm。对于压缩试样，高径比h0/d0=1，为了尽可能保证上下端面平行且光滑，进行反复研磨和测试。准静态拉伸和压缩实验在WDWE100D微机控制电子式万能试验机上进行，夹头向下拉伸和压头下压速度均为0.5 mm/min。压缩实验时，在试样上下端面涂覆强化润滑剂，压下量为50%时停止实验。

管段压缩与实心圆柱压缩相似，其压缩曲线同时受到端面摩擦状态和高径比h0/d0的影响。为了获得较为理想的单轴压缩应力应变曲线，只能利用外推法间接地推出d0→0时无摩擦影响的真实应力应变曲线，这将花费很多精力和时间，且存在不可排除的误差。因此，为了简化，将标距l0=100 mm的管轴向拉伸和h0/d0=1轴向压缩的工程应力应变曲线标示于图1。管拉伸和压缩曲线的弹性段未能重合，在弹性阶段，拉压曲线明显存在不同的线性应力应变关系（拉伸弹性模量E=74 GPa，压缩弹性模量Ec=54 GPa）。其最主要原因是无法保证压缩试样上下端面绝对平行（尽管反复研修并做了大量实验），同时，压缩试样上下端面不可避免的流动摩擦导致压缩处于非单轴应力状态。实际上，管材在拉拔成形时晶粒被拉长，择优取向使得变形后晶粒的长轴与拉拔方向即管材轴向平行排列，形成纤维组织和变形织构，而材料中所含杂质也在拉拔时沿管材轴向断续分布，这些都导致管材具有明显的各向异性。另外，拉伸和压缩在管材固有各向异性主轴系统中所施加的作用力方向恰恰相反，因此管材拉、压实验时可能表现出不同的弹性性质。

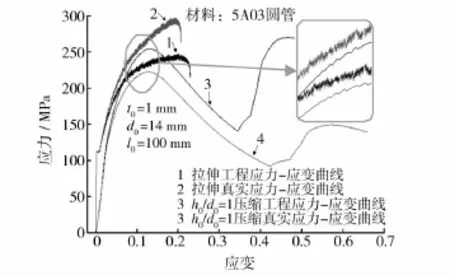
图1 5A03管材轴向拉伸和压缩的应力-应变曲线Fig.1 Axial tensile and compression stress-strain curves of the 5A03 tube

在未发生鼓凸失稳的均匀压缩时，管压缩时上下端面存在摩擦，导致端面附近材料很难沿径向和周向流动，该摩擦影响区域从开始变形时就脱离了单轴压缩应力状态。考虑到管段试样的横截面积较小，这种横向滑动摩擦的影响也相对减小，离开摩擦影响区的管试样轴线方向在中部附近，近似处于单轴压缩状态。设试样初始高度和压缩过程中的瞬时高度分别为h0和h，其工程应变和真实应变分别表示为:

在压缩载荷Fz作用下，假设管横截面圆环形状仍保持不变，面积由A0变为A，管外径和壁厚分别变为d和t时，工程应力和真实应力可分别表示为:

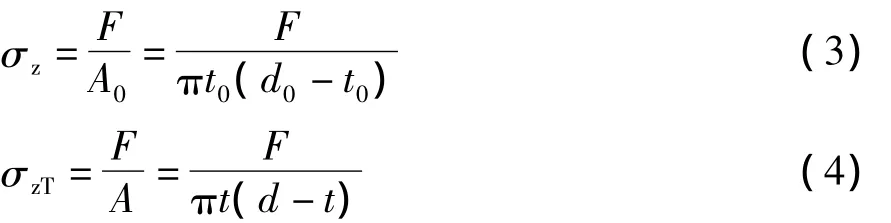
根据体积不变条件Ah=A0h0，真实应力σzT与工程应力σz具有如下关系:

由式（5）可以看出，由于管压缩过程中横截面积增大，σzT＜σz，其比值具有管试样瞬时压缩高度与原始高度之比h/h0的线性关系。与单轴拉伸时相反，即（压缩）变形程度越大，真实应力越小。

由图1可以看出，拉伸曲线有明显的屈服平台，ReL=111 MPa;而压缩时屈服点不明晰，取Rpc0.2=102 MPa，则有Rpc0.2＜ReL。分析认为，尽管管材拉拔成形后需经退火处理，但不能保证残余应力和残余应变完全消除，即实验前的管材相当于存在一个预拉伸变形，轴向拉伸时为同向加载，而压缩时则相当于反向再加载，因而由于包申格效应导致拉伸屈服强度略高于压缩屈服强度。屈服后，拉压应力-应变曲线出现了锯齿段波动（图1中箭头所示），这是大多数铝合金材料动态应变时效的典型宏观表现［17］。光滑形变阶段产生了加速溶质原子扩散所需的空位，可动位错和扩散中的溶质原子之间交互作用，从而在拉伸曲线上出现锯齿波。压缩应力应变曲线表现出典型的屈曲失稳特性，如果近似取压缩曲线的第一个峰值为管材的压缩强度，对于高径比h0/d0=1的试样（刚度影响较小），压缩强度略高于抗拉强度，这与多晶材料压缩变形时的位错运动塞积程度高于拉伸变形有关，因而前者的加工硬化率更显著，抗压强度略高于抗拉强度。

此外，管材抗拉强度（颈缩点工程应力）Rm略小于h0/d0=1的试样压缩时的最大工程应力Rmaxc，并且，前者产生在拉伸变形后期，而后者产生在变形初期。符合一般金属压缩强度要高于抗拉强度的规律。材料在拉力的作用下伸长，微观上表现为原子与其相邻原子之间的距离越来越远，吸引力也越来越小;而在压力的作用下，原子与其相邻原子之间的距离越来越近，排斥力会快速增加，因而有Rmaxc＞Rm。

2 影响管材轴向压缩失稳的实验及有限元分析

2.1 高径比对压缩失稳形式的影响

一般塑性材料在拉应力状态下都会产生极限应力，载荷继续增加的后果将是断裂;而压缩时的应力状态软性系数很大，塑性材料几乎不会发生剪裂，在最大压缩应力Rmaxc之后继续压缩，通常会发生形状失稳或压溃现象。一般压缩载荷先达到一个初始峰值，该峰值基本对应于鼓凸过程的开始，随后载荷急剧下降，之后的波动起伏是由于连续鼓凸或褶皱而形成的。图2所示为h0/d0为0.57，0.93，1.0，1.64时，4个管试样压缩失稳过程。由于h0/d0＜2，发生的屈曲有别于细长杆件压缩时的弹性屈曲，屈曲应力远大于材料初始屈服强度，因此，属于典型的塑性屈曲。与实心圆柱体镦粗不同，管料轴向压缩时，上下端面与压头和工作台接触面积小，而使摩擦的影响相对较小，几乎不存在黏着区。当h0/d0＜1时，受上下端面周向材料约束和摩擦影响，变形非常小，轴向压缩只能由附近材料的径向和周向流动来平衡，变形集中在受端面摩擦影响最小的试样中间的局部区域，压缩中后期形成一个鼓凸;当h0/d0＞1时，压缩变形初期，由于试样轴向长度较大，上下两部分的变形很难传递至试样中部，而在两端面附近形成2个微小鼓凸，而后靠近动压头的上鼓凸逐渐变大，产生局部失稳的上鼓凸被压实后，下鼓凸才开始逐渐增大发生失稳变形;而当h0/d0=1时，压缩初始阶段在上下端面附近同样具有鼓凸趋势，继续压缩，上部逐渐形成明显鼓凸，而在压下量达到50%时，下部鼓凸还没能形成。

图2 压缩实验过程Fig.2 Compression process of the 5A03 tube

由大量管压缩实验可知，两端面在相同摩擦条件而产生双鼓凸时，上鼓凸的形成总是先于下鼓凸的形成。分析认为，这可能是由于万能试验机工作时下工作台静止不动，动力由上压头提供，压缩载荷由管试样上部向下传递，因而形成双鼓时的第一个鼓凸首先在管段上部形成。

2.2 端面摩擦对压缩失稳的影响

压缩实验时，管试样上下端面均涂覆等量的二硫化钼润滑脂。为研究摩擦对管压缩的影响，并避开摩擦因数测试的困难，利用Dynaform有限元软件进行改变摩擦因数的有限元模拟，所建三维有限元模型如图3所示。模型采用实体单元，管外径和厚度设置为与实验相同，即d0=14 mm，t0=1 mm。压缩加载速率在某一定范围内变化对模拟结果影响很小，因而为缩短计算时间，压缩加载速度选用500 mm/min。

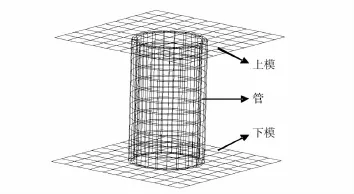
图3 圆管轴向压缩的有限元模型Fig.3 Finite element model for axial compression of circular tube

为考察摩擦的影响，在管试样上下端面和压头、工作台表面分别设置2组相反的摩擦因数μ，即:上端面摩擦因数μu=0.2，下端面摩擦因数 μd=0.05;μu=0.05，μd=0.2。h0/d0=3.0 时，管的压缩过程及材料位移云图的有限元模拟结果如图4所示。可以看出，摩擦因数μ较小侧，端面附近材料在径向和周向流动较大，沿压缩方向的轴向流动小;μ较大侧，材料轴向流动较大，而径向和周向流动相对小，这说明，有限元模拟结果基本符合塑性变形体积不变规律。由此，在不计压缩载荷传递方向和应变速率沿管轴向非均匀分布的影响时，摩擦因数越大，易于沿轴向流动的材料将逐渐向横向流动困难的管料外侧贴覆，在达到临界载荷时即迅速形成失稳鼓凸。正如有限元模拟结果所显示的，鼓凸总是在端面摩擦强烈一侧率先形成。

图4 不同摩擦条件下管压缩时材料位移云图的有限元模拟结果Fig.4 Finite element simulation results of displacement nephogram during the test under different friction conditions

2.3 管失稳鼓凸后的压溃

图5 管压溃失稳后的端面形状变化及质点第一主应变分布Fig.5 Shape change and particle first principal strain distribution for the end face of the tube after crushing instability

图5所示为h0/d0=1.64的管试样失稳鼓凸后，继续加载压缩至某一阶段的实验和有限元模拟结果，它们的形状比较接近。管压溃失稳时，鼓凸部分的外轮廓和端面内孔均沿同一方向变成了长圆形，后者尤为显著。鼓凸外形长轴直径dol=19.4 mm，短轴直径dow=18.6 mm;内孔长轴直径dil=11.8 mm，短轴直径dIiw=10.9 mm。鼓凸外径增大由管壁材料压溃和轴向堆积引起，当压溃端外径增大到一定值时，轴向压缩变形的位置发生转移，另一端鼓凸开始形成。端面内孔直径减小，是端面材料向横截面中心方向非轴对称流动变形所致。有限元计算结果显示，管端面变形主要集中在长轴端附近，产生了较强的径向和周向压缩变形，管壁增厚。而由于管横截面周向材料连续性的约束，短轴端附近材料主要发生向管横截面中心方向的刚性流动，管壁厚度略有减小。

圆管轴向压溃实验结果，既不同于圆环模式压溃，又不同于所谓钻石压溃模式，而属于一种具有一定规律性的非轴对称屈曲压溃。通常，圆环压缩的端面摩擦因数小时，端面内径会扩大，摩擦因数增大到一定数值时，内径开始收缩。而本实验中，由于材料非轴对称流动，使压缩管鼓凸和端面内孔均发生不同程度的畸变，除去管材各向异性影响外，可能还存在更为复杂微观机制和宏观力学方面的影响因素，这将成为后期研究的一项重要内容。

3 结论

1）根据高径比h0/d0=1的管试样压缩与原始标距l0=100 mm的试样的拉伸实验结果判断，5A03铝合金圆管具有拉、压双模量的倾向，拉伸屈服强度略低于压缩屈服强度，抗拉强度略低于抗压强度，且拉伸与压缩均呈现锯齿波屈服特性，拉伸时尤为显著。

2）管材高径比h0/d0影响其压缩失稳形式。本实验条件下，h0/d0=1为产生单鼓和双鼓的临界值。高径比小于该临界值时，薄壁圆管压缩将出现单鼓;高径比大于该临界值时，薄壁圆管压缩将出现双鼓。

3）管材端面与压头和工作台表面之间的摩擦条件影响失稳鼓凸出现的先后。摩擦因数越小，失稳鼓凸出现越晚。对于两端面摩擦系数不等的压缩实验，摩擦因数较大的一侧优先形成鼓凸。

［1］LIN Yan，YANG He.Thin-walled Tube Precision Bending Process and FEM Simulation.In:Proceedings of the 4th International Conference on Frontiers of Design and Manufacturing［C］//Beijing:InternationalAcademic Publishers，2000:305—308.

［2］张敬文，鄂大辛，李延民，等.弯曲速度对弯管壁厚变化的影响［J］.精密成形工程，2012，4（1）:5—8.

ZHANG Jing-wen，E Da-xin，LI Yan-min，et al.Effects of Bending Velocity on the Change of Wall Thickness in Tube Bending［J］.Journal of Netshape Forming Engineering，2012，4（1）:5—8.

［3］张敬文，鄂大辛，李延民，等.弯模间隙对5A06管弯曲横截面畸变及壁厚变化的影响［J］.精密成形工程，2012，4（2）:19—22.

ZHANG Jing-wen，E Da-xin，LI Yan-min，et al.Effects of Clearance on Cross Sectional Distortion and Wall Thickness Variation of 5A06 Tube［J］.Journal of Netshape Forming Engineering，2012，4（2）:19—22.

［4］林芳，鄂大辛，张敬文.单元类型对有限元计算弯管截面畸变及壁厚变化的影响［J］.精密成形工程，2012，4（3）:10—13.

LIN Fang，E Da-xin，ZHANG Jing-wen.Effects of Element Types on Cross Sectional Distortion and Wall Thickness Variation in Finite Element Simulation［J］.Journal of Netshape Forming Engineering，2012，4（3）:10—13.

［5］徐海斌，张德志，谭书舜，等.轴向压缩的金属薄壁圆管相似律的实验研究.第20届全国结构工程学术会议论文集（第Ⅰ册）［C］//北京:工程力学杂志社，2011:554—559.

XU Hai-bin，ZHANG De-zhi，TAN Shu-shun，et al.Experimental Study on Similarity Criterion for Axial Compression of Thin-walled Circular Metallic Tubes.In:Proceedings of the 20th National Conference on Structural Engineering.No.I［C］//Beijing:Engineering Mechanics Press，2011:554—559.

［6］GUILLOW SR，LU G，GRZEBIETA R H.Quasi-static Axial Compression of Thin-walled Circular Aluminum Tubes［J］.International Journal of Mechanical Sciences，2001，43（9）:2103—2123.

［7］SONG Jie，ZHOU Yu-feng，GUO Feng-lin.A Relationship Between Progressive Collapse and Initial Buckling for Tubular Structures under Axial Loading［J］.International Journal of Mechanical Sciences，2013，75:200—211.

［8］BORIA S，PETTINARI S，GIANNONI F.Theoretical Analysis on the Collapse Mechanisms of Thin-walled Composite Tubes［J］.Composite Structures，2013，103:43—49.

［9］HONG Wu，FAN Hua-lin，XIA Zhi-cheng，et al.Axial Crushing Behaviors of Multi-cell Tubes with Triangular Lattices［J］.International Journal of Impact Engineering，2013，63:106—117.

［10］GUPTA P K，GUPTA N K.A Study on Axial Compression of Tubular Metallic Shells having Combined Tube-cone Geometry［J］.Thin-walled Structures，2013，62:85—95.

［11］吴进，贾芬，王蒙蒙，等.石膏型渗流制备泡沫铝填充圆管压缩行为研究［J］.精密成形工程，2011，3（4）:22—25.

WU Jin，JIA Fen，WANG Meng-meng，et al.Study on Compressive Behavior of Foam-filled Tubes Prepared by Gypsum Mould Infiltrating Casting［J］.Journal of Netshape Forming Engineering，2011，3（4）:22—25.

［12］陈吉生，鄂大辛，张敬文.1Cr18Ni9Ti管材拉伸断裂过程中裂纹扩展的研究［J］.兵工学报，2013，34（7）:865—868.

CHEN Ji-sheng，E Da-xin，ZHANG Jing-wen.Research on Crack Propagation in the Crack Process of 1Cr18Ni9Ti Tube Under Uniaxial Tension［J］.Acta Armamentarii.2013，34（7）:865—868.

［13］陈吉生，鄂大辛，张敬文.材料模型对1Cr18Ni9Ti管材拉伸有限元仿真的影响［J］.精密成形工程，2012，4（4）:10—12.

CHEN Ji-sheng，E Da-xin，ZHANG Jing-wen.Effects of Material Models on Finite Element Simulation for Uniaxial Tension of 1Cr18Ni9Ti Tube［J］.Journal of Netshape Forming Engineering，2012，4（4）:10—12.

［14］刘娟，鄂大辛，张敬文.小直径薄壁管直接拉伸方法研究［J］.实验技术与管理，2012，29（3）:56—58.

LIU Juan，E Da-xin，ZHANG Jing-wen.Study on Tensile Method of Thin-walled Tube with Small Diameter［J］.Experimental Technology and Management，2012，29（3）:56—58.

［15］E Da-xin，HE H H，LIU X Y，et al.Spring-back Deformation in Tube Bending［J］.International Journal of Minerals，Metallurgy and Materials，2009，16（2）:177—183.

［16］E Da-xin，LIU Y F.Springback and Time-dependent Springback of 1Cr18Ni9Ti Stainless Steel Tubes under Bending［J］.Materials and Design，2010，31（3）:1256—1261.

［17］钱匡武，李效琦，肖林钢，等.金属和合金中的动态应变时效现象［J］.福州大学学报（自然科学版），2001，29（6）:8—23.

QIAN Kuang-wu，LI Xiao-qi，XIAO Lin-gang，et al.Dynamic Strain Aaging Phenomenon in Metals and Alloys［J］.Journal of Fuzhou University（Natural Science），2001，29（6）:8—23.