基于Bayes方法的某武器系统可靠性综合评估

王晓铭，曹颖颖

（1.中国人民解放军海军驻上海地区航天系统军事代表室，上海 201109；2.上海机电工程研究所，上海 201109）

0 引言

工程中可靠性的精确限评定方法采用系统可靠性评估模型时过于复杂，计算不便，可靠性评估困难，故工程中系统可靠性评估一般采用近似评定方法［1］。对武器系统可靠性评估，一般是将系统视作寿命符合某种分布类型的单元，按国军标提供的试验方案进行可靠性试验，利用现场试验数据对系统的可靠性进行评估。仅依靠现场试验数据评估系统的可靠性，试验时间较长，且结果常会过于保守或风险过高［2］。以某武器系统单火力通道舰面设备为例，其严重故障平均时间间隔（MTBCF）规定值为100h，最低可接受值为60h，试验区制定的试验方案总试验时间为284h。按当时的试验条件，每天只能进行8h试验，假定过程中不出现任何故障，完成系统可靠性试验需35d。实际上，武器系统研制过程中已对分系统或系统进行了大量的可靠性试验，并有相应的数据，可利用这些历史数据，结合现场试验的数据对系统的可靠性进行评估，以提高评估的置信度或在置信度不变的前提下缩短现场试验时间。本文采用Bayes方法，利用武器系统各分系统的可靠性鉴定数据以及现场系统可靠性鉴定数据对某武器系统的可靠性进行了综合评估。

1 基于Bayes方法的系统可靠性综合评估原理及步骤

系统可靠性综合评估一般是金字塔式的评估过程：从系统的最底层级别开始，利用可靠性评估模型得到上一级别评估信息，即组件级别的可靠性评估折合信息，与组件级别的试验信息综合获得该级别的可靠性评估信息。上述折合与综合可靠性信息过程，自下而上逐级别地一直进行到系统级别，得到系统级的可靠性评估信息，进行系统的可靠性评估。实际研制过程中，在各阶段武器系统有或多或少的更改，因此在最终评估时，只选择与当时技术状态相差较小的阶段的历史数据。评估的基本步骤如下。

a）根据单元可靠度的验后分布求出其M阶验后矩E［Rji］，i＝1，2，…，n，j＝1，2，…，M。此处：n为系统中单元数量；M为验后矩阶数。

b）根据系统组成结构和各组成部分的可靠度Ri确定系统可靠度函数的表达式Rs＝Rs（t）＝Φ（R1，…，Rn）。此处：Ri＝Ri（t），i＝1，2，…，n。

c）求得系统可靠度的验前一阶矩μ和二阶矩υ的表达式，将各单元可靠度的验后一μ＝E［Ri］，υ＝E［R2i］代入求得系统可靠度的验前一阶矩μ＝E［R］，υ＝E［R2］。

d）选择合适的函数拟合系统可靠度的验前分布，利用各单元的可靠度验后矩求得系统可靠度的验前分布的参数，结合系统试验数据得到系统验后分布及其参数，即可计算给定置信度的系统可靠度近似下限。

若单元或系统存在验前信息，则应作如下处理：单元存在验前信息时，各单元参数中需包括验前参数，综合到系统的一阶矩和二阶矩；系统存在验前信息时，可假设各单元验前可靠度的一阶矩和二阶矩相等，将系统的验前信息分配至各单元。一般只对成败型单元和指数型单元进行验前信息的综合或分配［3］。

2 武器系统可靠性综合评估

目前武器系统多为多通道，整个武器系统由各级分系统组合而成，如图1所示。其中：只考虑一级分系统，并假设武器系统有m个分系统和n个火力通道。

图1 武器系统组成Fig.1 Composition of a weapon system

2.1 试验数据

对某武器系统（分系统5个，火力通道4个），本文基于可靠性试验数据，用Bayes方法对其单通道可靠性进行分析。

设计定型期间组织对该武器系统进行了专项系统级可靠性试验。根据当时系统组成仅进行了两个通道的试验，试验结果见表1。武器系统研制阶段各分系统可靠性鉴定试验的试验结果见表2。其中：分系统5的可靠性试验未在综合环境试验箱中进行，故增加了环境因子，经设计方、用户方与国内同行专家打分，其值确定为1.5，其等效试验时间为164／1.5＝109.3h。

表1 专项系统级可靠性试验数据Tab.1 System-level reliability test data

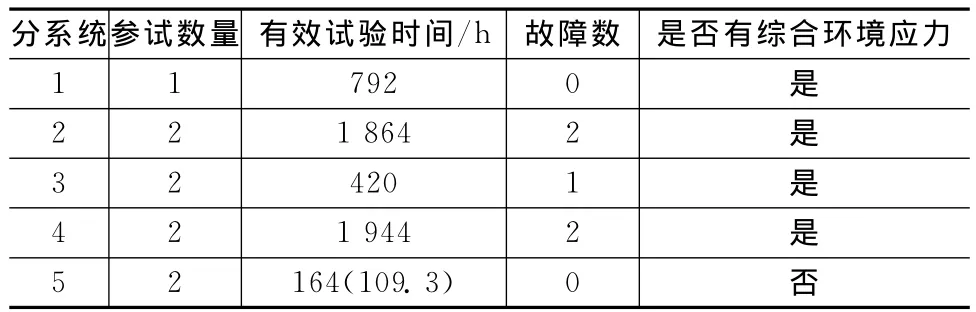
表2 分系统可靠性鉴定试验数据Tab.2 Subsystem-level reliability test data

2.2 可靠性综合评估

因从研制试验阶段至定型试验阶段，武器系统各设备主要技术状态较稳定，故认为分系统的可靠性试验数据与研制试验阶段及设计定型阶段系统可靠性数据为同一母体试验数据，可用本文讨论的Bayes方法进行系统的可靠性综合评估。其中各分系统的可靠性鉴定试验数据为单元试验数据，研制阶段及定型阶段的专项可靠性试验数据为系统试验数据。

对单通道系统来说，认为其是近似服从指数型分布单元的串联系统［4］。可靠性框图如图2所示。

图2 系统可靠性框图Fig.2 Reliability model of a weapon system

将分系统可靠性鉴定试验数据简单转换为单通道可靠性数据，结果见表3。

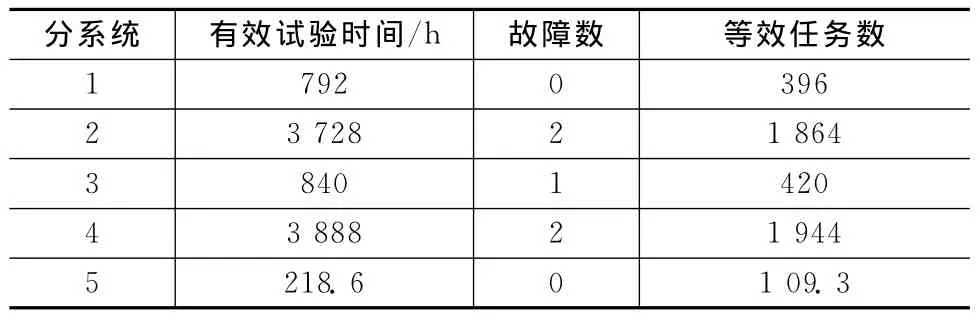
表3 单通道可靠性试验数据Tab.3 Reliability test data of a single channel

综合系统与分系统的可靠性试验参试设备及试验数据，分三种情况在给定置信度γ＝0.7条件下对武器系统单通道的可靠性进行评估［5］。

a）系统取无信息先验分布，仅利用分系统的试验数据对系统进行可靠性评估。

各分系统为指数型分布单元，用Bayes方法用负对数Γ分布拟合可靠度的分布函数。系统取无信息先验分布，即系统的可靠性先验分布为L（Γ（z0，η0）），其 中 先 验 参 数，先 验 失 效 数z0＝0.522 197 500 6，先 验 等 效 任 务 数η0＝3 608 679 124。

将系统的先验一阶矩和二阶矩分配到各分系统，得到各分系统的等效失效数z0i＝z0／5＝0.104 439 500 12，等 效 任 务 数η0i＝η0＝3 608 679 124。各分系统的验后分布参数为（zi＋z0i，ηi＋η0i），验后分布见表4，可得各分系统的验后两阶矩见表5。

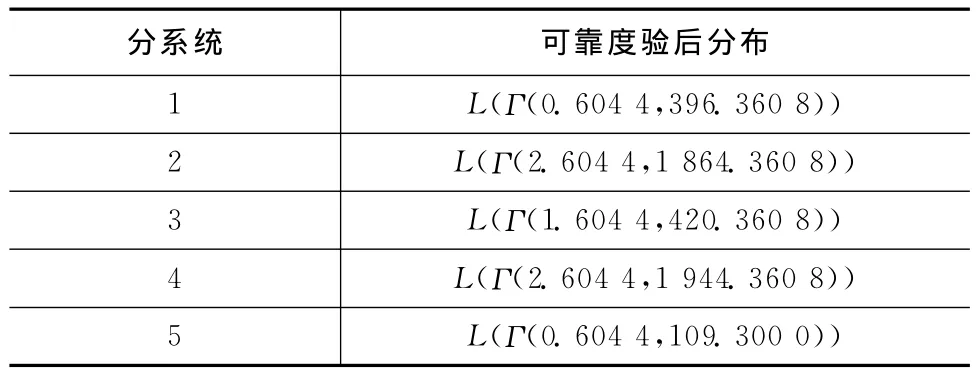
表4 各分系统验后分布Tab.4 Posterior distribution of various subsystem

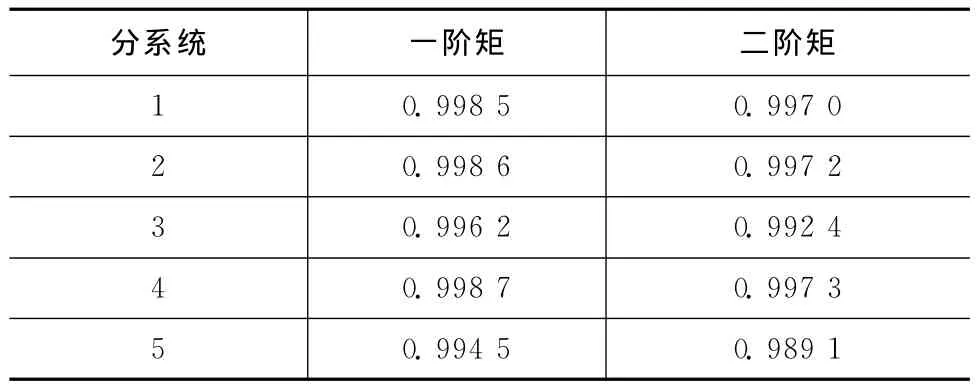
表5 各分系统前两阶矩Tab.5 First and second moment of various subsystem

编程算得单元折合到系统的等效失效数z＝1.513 2，等效任务数η＝110.830 0。则可得武器系统单通道设备可靠性的Bayes近似下限＝0.983 455。

b）系统取无信息先验分布，综合系统和分系统试验数据对系统进行可靠性综合评估。

系统的现场可靠性试验数据为：z′＝1.5，η′＝141.38。综合分系统折合到系统的等效试验数据，得到系统总的等效失效数和等效任务时间z″＝z＋z′＝2.909 6，η″＝η＋η′＝204.834 0。编程算得武器系统单通道设备可靠度的Bayes近似下限＝0.982 984。

c）仅用系统可靠性试验数据对系统进行可靠性评估。

由可得武器系统单通道设备可靠度的点估值，估计下限分别为

式中：η0为研制试验中的等效任务数；η为定型试验中的等效任务数；Z0为研制试验中的故障数；Z为定型试验中的故障数；t0为有效任务时间；γ为置信度。可算得武器系统单通道的任务可靠度点估值为0.986，在0.7置信度下，任务可靠度置信下限为0.983。

2.3 评估结果

武器系统单通道可靠度Bayes近似评估的结果见表6。

表6 武器系统单通道可靠度Bayes近似评估结果（γ＝0.7）Tab.6 Approximate assessment results of a signle-channel weapon system （γ＝0.7）

3 结束语

本文用系统Bayes近似评估方法对某武器系统单通道设备的可靠性进行了评估，说明了本文方法的可行性，因评估方法的限制条件，本文分析评估过程中仅利用了相同母体和综合环境中的试验数据。当现场试验数据较充足时，利用现场试验数据得到的结论是最真实的，但当现场数据较少时，通过适当方法将现场试验之前的系统或分系统可靠性试验数据转化作为现场可靠性评估的先验信息，可提高用于评估的信息量。应用于工程实践中，即如在武器系统研制过程中分系统有大量的可靠性试验数据，或系统有充分的先验信息和可靠性试验数据，就可利用这些分系统的试验数据和系统先验信息对系统进行可靠性评估，而在设计定型试验期间，系统级的可靠性试验时间能适当减少。这样既可缩短试验的时间又能降低试验成本。

［1］ 金 星，洪延姬.系统可靠性评定方法［M］.北京：国防工业出版社，2005.

［2］ 王建霞，郭 波.融合研制各阶段试验信息的成败型产品可靠性Bayes评估［J］.兵工自动化，2006，12（1）：31-32.

［3］ 李 荣.复杂系统Bayes可靠性评估方法研究［D］.长沙：国防科学技术大学，1999.

［4］ 蒋仁言，左明健.可靠性模型与应用［M］.北京：机械工业出版社，1999.

［5］ 金 星，洪延姬，沈怀荣，等.可靠性数据计算及应用［M］.北京：国防工业出版社，2003.