强信号背景下弱信号角度时延的联合Capon估计方法

冯 源，侯 帅，陈 强，迮剑舟，孙 云

（1.中国人民解放军73017部队，江苏 南京 211122；2.安徽省电子制约重点实验室，安徽 合肥 230037；3.中国人民解放军73676部队，江苏 无锡 214063；4.阳春科技有限公司，江苏 南京 211100）

0 引言

在近年来的电子对抗领域中，各种新式武器，尤其是各种隐身技术以及精确制导武器的出现，给现代电子战双方提出了新的挑战。利用外辐射源信号，如以民用通信、广播、电视台等发射的电磁波为照射源，对敌目标进行有效的探测和定位，成为重要的发展方向。在利用民用广播电台信号对目标进行无源定位的过程中，在强直达波干扰背景下对微弱目标的DOA、时延以及多普勒参数进行准确而又快速的估计非常重要。实际情况下，强直达波通常方位是固定且可精确测量［1］。因此，本文将从先验知识的角度（强直达波信号角度已知，且强度远大于目标回波信号）研究强信号干扰背景下目标角度与时延的联合估计问题。MUSIC，Pro-ESPRIT等性能优良的子空间类角度与时延联合估计算法，须精确已知信源个数用以正确构造信号与噪声子空间［2－3］。但在强直达波干扰下，采用已有的Akaide信息论AIC准则或最小描述长度（MDL）估计信源数存在较大偏差［4］。Capon谱估计法常用于DOA的估计，优势是不需要信源数的先验已知或估计信源数，其采样数据长度的门限较低，劣势是无法突破瑞利限的限制，DOA估计的分辨力较低［5］。本文对强信号背景下弱信号角度时延的联合Capon估计方法进行了研究。

1 信号模型

设某一阵列天线接收到的一个广播电台的直达信号为s（t），若不考虑多径效应则会有一路强直达波信号与P个经目标反射后的弱信号入射到N元阵列上，此阵列为各向同性阵元组成的半波长均匀线阵，且P＋1个接收信号均为窄带信号（P＋1＜N），则阵列接收向量 ［r1（t）r2（t） …rN（t）］T＝r（t）可表示为

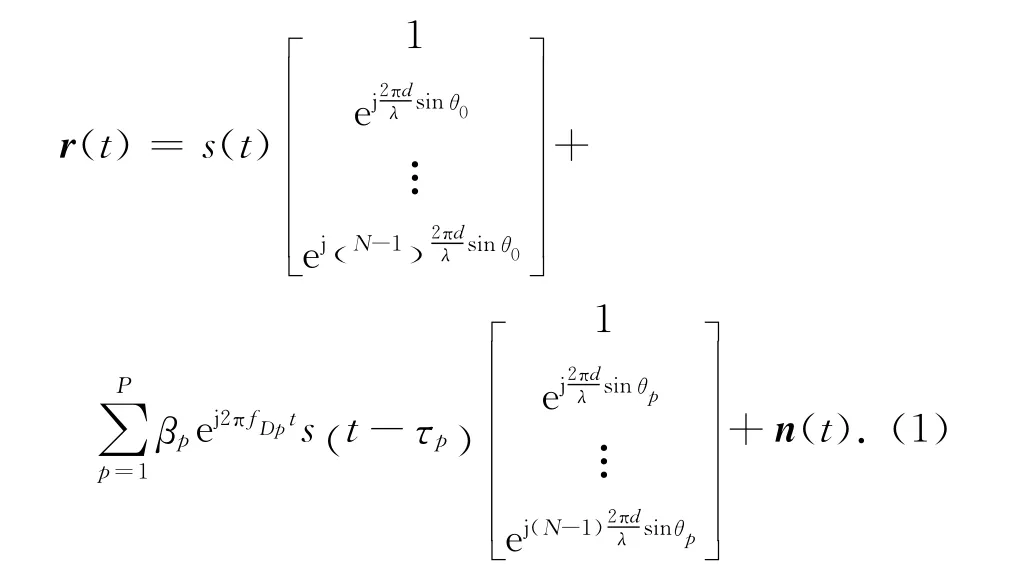
式中：θ0为强直达波来波方向；θ1，…，θP为弱信号的来波方向，τ1，…，τP为各路弱信号相对强直达波的时延；d为阵元间距，且d＝λ／2；λ为入射信号频率。记μp（t）＝βp（t）ej2πfDpt，则r（t）可写成

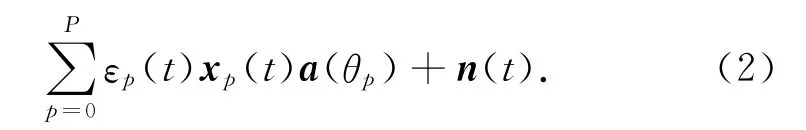
为简化分析，且忽略各目标的多普勒频移，即fDp＝0。研究对各目标来波方向与相对直达波的时延（θp，τp）进行联合估计。

2 Capon谱估计原理与改进Capon方法

2.1 Capon谱估计方法原理

Capon法的要点是求解权值

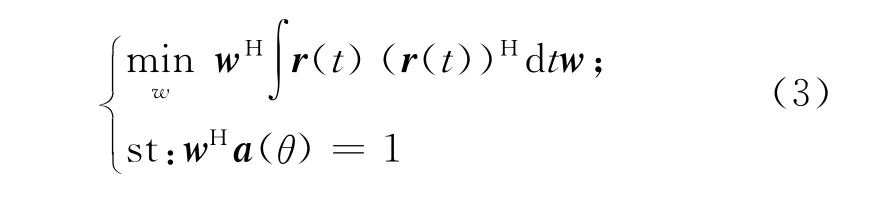
的优化问题［6－7］。即搜索目标可能出现的角度，使在搜索方向取得一定功率的条件下总的接收功率最小。根据式（3）求解出权值得

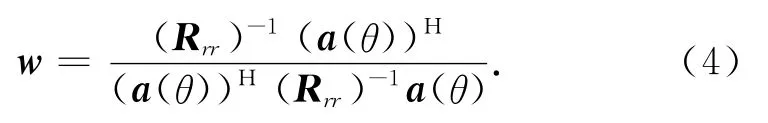
式中：Rrr为阵列输入信号的协方差矩阵，且Rrr＝∫r（t）（r（t））Hdt。

在用Capon法进行DOA估计时，用得到的权值计算输出信号的空间谱函数，有

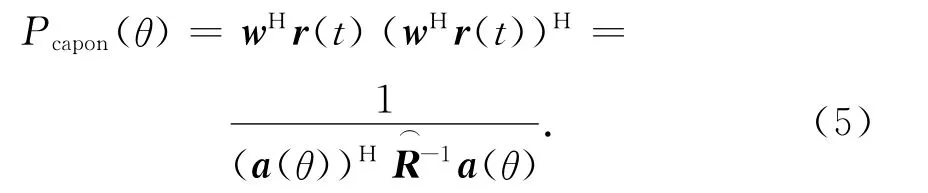
与谱峰对应的所有θ即为波达方向的估计

当噪声仅为高斯白噪声，对任意θ，Pcapon（θ）均是来自方向θ的信号功率的最大似然估计，其空间谱正比于该方向的信号功率，但受阵列孔径限制，角度分辨率较低，无法分辨1个波束宽度内的2个信号。但此算法的优点是无需已知或估计信源数，其采样数据长度的门限较低。

2.2 改进的Capon法联合估计信号DOA与时延

基本的Capon谱估计算法只能对DOA进行估计而无法对DOA与时延进行联合估计。本文对基本的Capon谱估计方法进行改进，使之能对DOA和时延进行联合估计。

由上述分析可知，用Capon谱估计法进行信号DOA估计时，求得权值向量w后即构造了输出信号的空间谱函数［式（5）］。本文提出的方法先不计算空间谱函数，再求得各阵元的信号加权求和输出

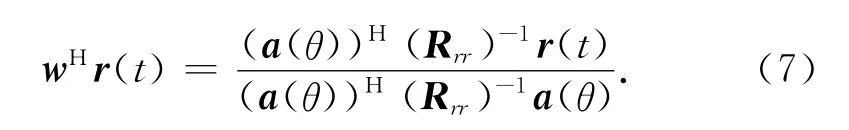
将加权输出的信号与取不同时延τ的直达波信号进行积分，可得

本方法利用强弱信号能量差别大的特点，将直达波信号s（t）用第一路天线（参考天线）接收到的信号r0（t）代替，即s（t－τ）＝r0（t－τ）。绘制ρ（θ，τ）的三维图谱，ρ（θ，τ）形成谱峰的位置即对应目标的角度和相对时延。需说明的是，为避免强直达波信号对结果的干扰，角度和时延搜索时避开了强直达波信号所在的角度以及零时延周围的区域，以免直达波信号太强而覆盖了目标信号。

2.3m-Capon算法

在上述的改进Capon法中，当两个目标信号的来波方向靠得过近时，方法的估计性能将严重下降，甚至无法区分两个信号。以下利用MUSIC算法的高分辨特性对上述方法进一步优化，得到一种基于m-Capon的角度时延联合估计方法，该法能对空域中靠得较近的信号进行DOA和时延的联合估计。

在阵列信号处理当中，MUSIC算法是一种经典的子空间类DOA估计算法。与Capon法相比，它能突破瑞利限的制约，有更高的角度分辨力。MUSIC算法的空间谱函数可表示为

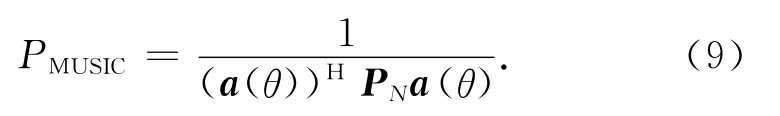
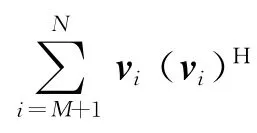
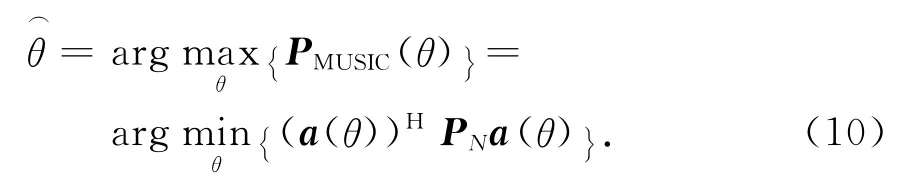
显然，PMUSIC并不是任何意义下的真实谱。严格地说，它仅是信号导向矢量与噪声子空间的距离，却能在真实波达方向的附近出现谱峰，可超分辨地估计各信号的波达方向［8］。但由于实际相关矩阵是通过有限快拍数据估计获得的，快拍个数很大程度上影响MUSIC方法DOA估计的性能，而且此方法须预先判定信源数和对相关矩阵进行特征值分解。

由上面分析可知，Capon方法直接利用相关矩阵进行DOA估计，无需预判信源个数，但该方法受瑞利限的制约，角分辨能力较差。MUSIC方法虽具有超分辨性能，但需估计信源数和对相关矩阵的特征值分解，而且对快拍数量的要求远远超过Capon算法，这往往成为限制其实际应用的主要因素。如结合两种方法的优点，就会得到一种更有效的DOA估计方法［8］。基于此，提出了m-Capon算法。

对阵列输入信号的协方差矩阵Rrr进行特征值分解，可得

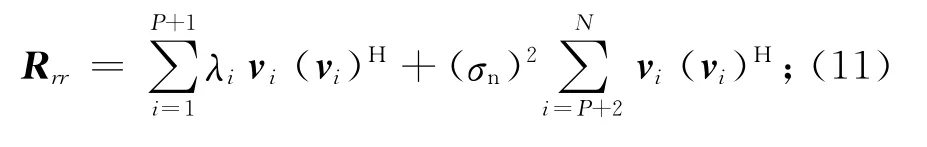
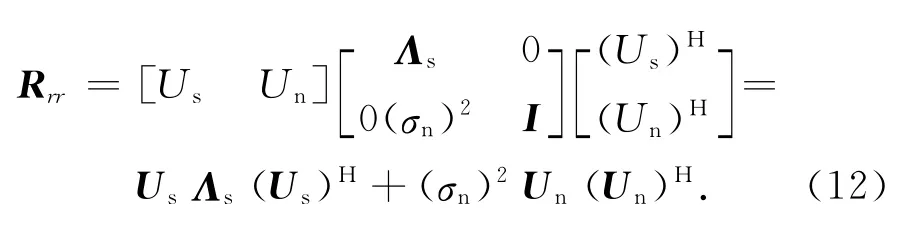
式中：Us，Un分别为信号子空间和噪声子空间矩阵，且

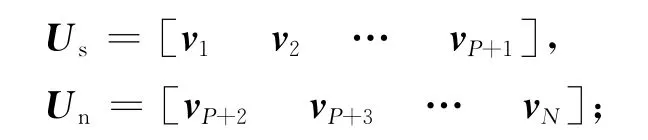
Λs为由信号对应的特征值构成的对角矩阵，且Λs＝diag［λ1λ2…λM］。进一步推导可得

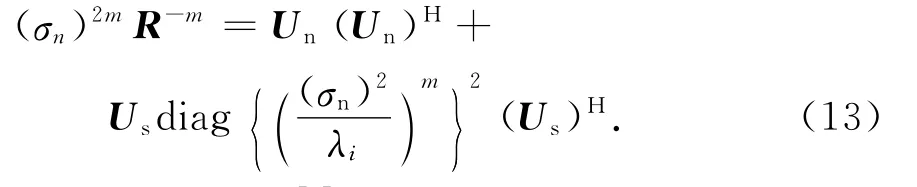
式中：m为任意整数［8］。因 （σn）2／λi＜1，当m趋近于无穷大时，式（13）中含有信号子空间的一项将趋近于0，即

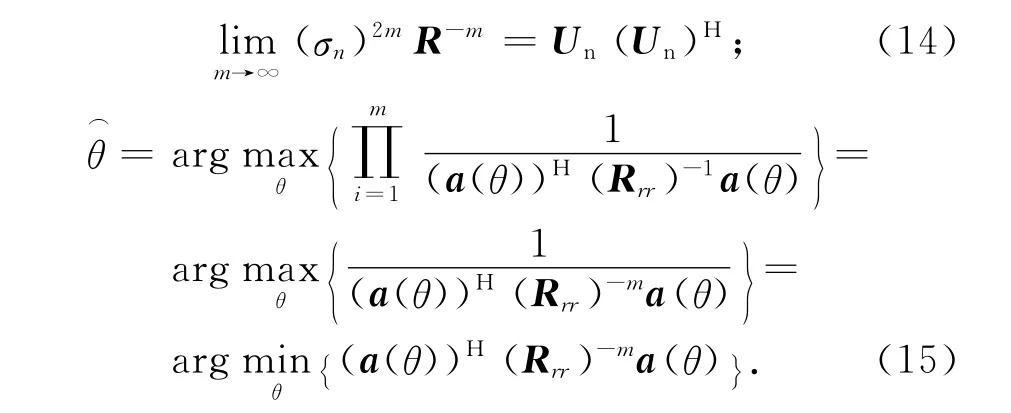
阵列接收信号的m-Capon谱可写成

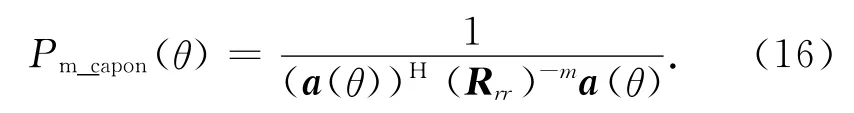
其物理意义相当于利用m个Capon估计器级联克服单个Capon估计器受瑞利限的制约，提高角度分辨力；当m＝1时，算法变为Capon谱估计法；当m→∞时，算法又变为MUSIC波达方向估计法。

2.4 改进的m-Capon方法

为提高改进的Capon法在目标来波方向接近时的角度时延联合估计性能，本文提出一种改进的m-Capon方法。该法将改进的信号Capon谱与信号的m-Capon谱相乘，得到阵列接收信号改进的m-Capon谱用于信号角度和时延的联合估计。具体步骤如下。

步骤1）跟据Capon谱估计原理计算出式（3）中的w，求得阵列的加权输出wHr（t）。

步骤2）将wHr（t）与取不同τ的第一路接收信号r0（t－τ）进行积分，可得改进的Capon谱

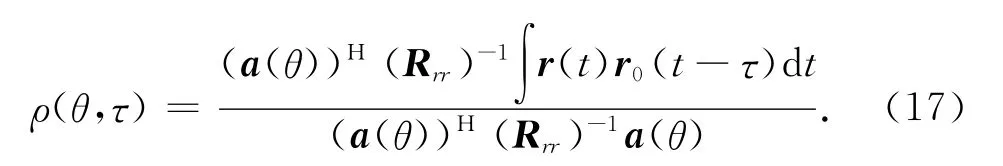
步骤3）由式（16）求得阵列输入信号的m-Ca-pon谱。

步骤4）将ρ（θ，τ）与m-Capon谱相乘，得到改进的m-Capon谱

改进的m-Capon方法原理如图1所示。

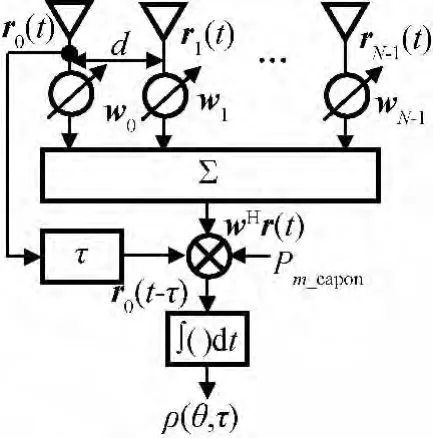
图1 改进m-Capon法的角度时延联合估计原理Fig.1 DOA and time-delay joint estimation based onm-Capon method

3 仿真

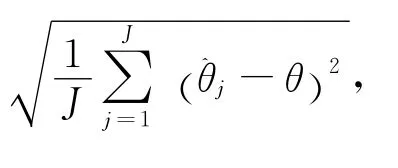
仿真1：改进m-Capon法的估计效果

设强直达波信号来波方向为0°，相对时延为0，信噪50dB；目标信号1的来波方向50°，相对时延0.5μs；目标信号2的来波方向55°，时延1.2μs；两信号信噪比均为10dB；快拍数K＝1 000，m＝4。仿真结果如图2所示。

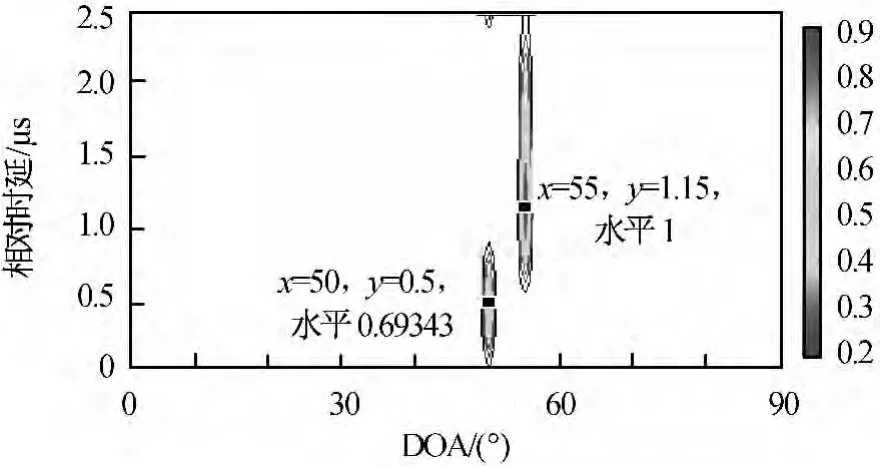
图2m＝4时改进m-Capon法估计效果Fig.2 Advancedm-Capon estimation performance whenm＝4

由图2中两个信号峰值所处的位置可知：改进的Capon方法可对目标信号的来波方向和相对时延进行有效的联合估计。

仿真2：不同m值和信号角度间隔条件下改进m-Capon法估计性能

设强直达波信号来波方向0°，相对时延0，信噪比50dB；目标信号1的来波方向50°，相对时延0.5μs；目标信号2的信噪比0dB，来波方向从52°变化至64°，时延1.2μs；K＝1 000，蒙特卡洛试验次数J＝100，结果如图3、4所示。

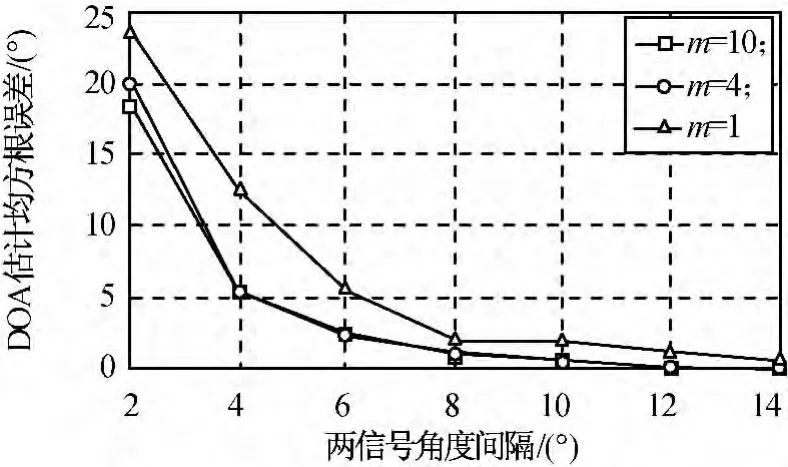
图3 不同角度间隔和m条件下DOA估计均方根误差Fig.3 RMSE of DOA estimation changed under various angel interval andm

由图3、4可知：引入m-Capon法，改善了改进的Capon方法的角度与时延联合估计性能。随着m值的进一步增大，性能改善的速度逐渐趋于平缓。

仿真3：不同信噪比条件下改进m-Capon法估计性能

设强直达波的信噪比固定为50dB，目标信号的信噪比从－20dB变化至20dB；K＝1 000，m＝4，J＝100。不同信噪比条件下DOA与时延估计的均方根误差分别如图5、6所示。

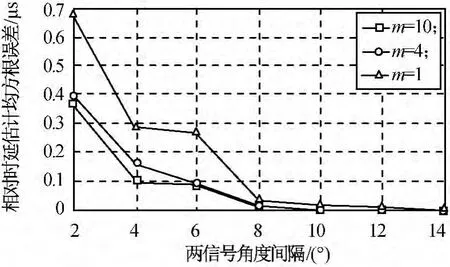
图4 不同角度间隔和m条件下时延估计均方根误差Fig.4 RMES of time-delay estimation performance changed with angel interval andm

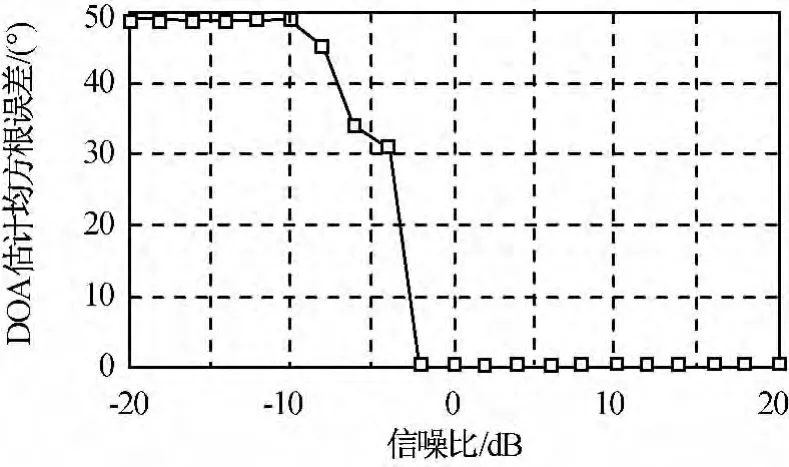
图5 不同信噪比DOA估计均方根误差Fig.5 RMSE of DOA estimation performance under various with SNR

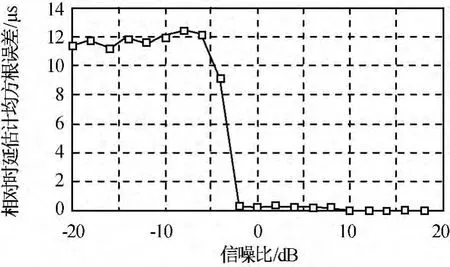
图6 不同信噪比的时延估计均方根误差Fig.6 RMSE of time-delay estimation performance under various SNR

由图5、6可知：本方法当信噪比大于0dB时有较好的估计性能；当信噪比小于0dB时，估计性能则有明显下降。

仿真4：不同快拍数的改进m-Capon法估计性能取强直达波的信噪比和目标信号的信噪比分别固定50，0dB；m＝4；J＝100，仿真所得DOA与时延估计的均方根误差分别如图7、8所示。

由图7、8可知：K的下降对DOA以及时延估计性能的影响有限，本方法在快拍数较少的条件下也可有效地对两个参数进行估计。

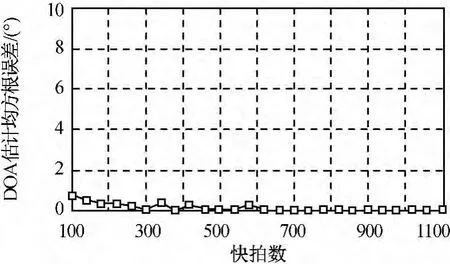
图7 不同快拍数的DOA估计均方误根差Fig.7 RMSE of DOA estimation performance under various snapshots

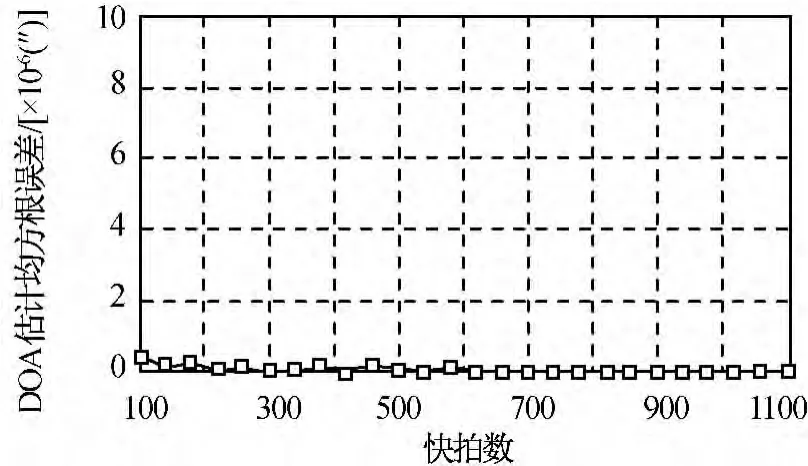
图8 不同快拍数的时延估计均方根误差Fig.8 RMSE of time-delay estimation performance under various with snapshots

4 结束语

针对强信号背景下的弱信号角度时延联合估计问题，本文提出了一种基于改进m-Capon法的联合估计方法。该方法无需估计弱信号的信源数，无需进行特征值分解，能区分来波方向接近的不同目标信号，同时在快拍数较少的条件下，也可有效地对弱信号的角度和相对强直达波的时延进行估计。

［1］ 陈 辉，苏海军.强干扰／信号背景下的DOA估计新方法［J］.电子学报，2006，34（3）：540-543.

［2］ VANDERVEEN M C，PAPADIAS C B，PAULRAJ A.Joint angle and delay estimation（JADE）for multipath signals arriving at an antenna array［J］.IEEE Communication，1997，1（1）：12-14.

［3］ 易 岷，让魏 平，肖先赐.动目标多径回波的时延、到达角和多普勒频率联合估计［J］.信号处理，2005，21（5）：427-433.

［4］ 徐 亮，曾 操，廖桂生，等.基于特征波束形成的强弱信号波达方向与信源数估计方法［J］.电子与信息学报，2011，33（2）：321-325.

［5］ 张涛麟，刘 颖，廖桂生.一种未知信源数的高分辨DOA估计算法［J］.电子与信息学报，2008，30（2）：375-378.

［6］ CAPON J.High resolution frequency-wave number spectral analysis［J］.Proc of the IEEE，1969，57（8）：1408-1418.

［7］ WAX M，KAILATH T.Detection of signals by information theoretic criteria［J］.IEEE Trans on ASSP，1985，33（2）：387-392.

［8］ 张 静，廖桂生，张 洁.强信号背景下基于噪声子空间扩充的弱信号DOA估计方法［J］.系统工程与电子技术，2009，31（6）：1279-1283.