目标机动条件下的定点伴飞控制方法研究

杨勤利，卢 山，朱思莉，夏永江

（1.上海交通大学 电子信息与电气工程学院，上海 200240；2.上海航天控制技术研究所 上海市空间智能控制技术重点实验室，上海 200233；3.上海航天技术研究院，上海 201109）

0 引言

在空间目标侦察、在轨服务等任务的需求牵引下，航天器的自主交会技术得到广泛的重视和开发。从早期以人手动操作为主的交会对接，逐渐向自主性、多样性发展［1－2］。具体表现在：整个任务期间可完全依靠星上自主完成，地面站仅起监控作用；从简单的交会对接发展成具备绕飞、定点伴飞等多种能力的多任务模式。

在原有载人交会对接的基础上对自主交会技术展开了大量的演示验证项目，如美国的DART、轨道快车，日本的ETS－VII，欧洲的ROGER等，均要求机动平台具有近距离定点伴飞能力，可对目标进行侦察、捕获等在轨操作［3］。目前国外初步掌握了对处于自由飞行状态的目标进行自主接近和定点伴飞技术，可用于工程实际任务。

针对目标存在机动的定点伴飞研究其潜在的用途，工程实际应用价值受到关注。因目标机动的控制力大小和方向未知，对合作目标的自主定点伴飞控制方法的控制效果的影响较大，甚至无法完成伴飞任务。文献［4］对目标机动的空间拦截进行了研究，在控制律设计中考虑将目标机动的加速度作为未知量，达到理想的控制效果。但对目标机动时的定点伴飞，目前国内外研究较少，其中的关键技术有待攻克。

本文对目标机动条件下机动目标的定点伴飞进行了研究。

1 不确定系统

1.1 相对轨道动力学

建立目标自由飞行时的追踪星定点伴飞相对轨道动力学方程。相对位置矢量如图1所示。图中：T为目标星；C为追踪星；D为定点伴飞的目标点。定义轨道坐标系So：原点为目标星质心；z轴沿径向指向地球；x轴垂直于z轴且沿速度方向；y轴符合右手定则，即沿轨道面的负法线方向。令rT，rC分别为目标星和追踪星相对地球的位置矢量，rTC，rTD分别为追踪星和目标点相对目标星的位置矢量；Δr为追踪星相对目标点位置矢量。

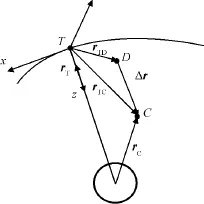
图1 相对位置矢量Fig.1 Vector of relative position

设目标星为自由飞行，则其轨道动力学方程可描述为

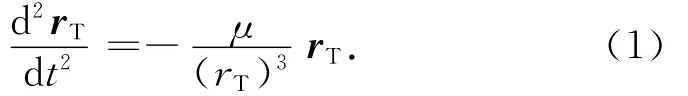
式中：μ为地球引力常数。

追踪星的轨道动力学方程考虑轨道控制，可描述为

式中：uC为追踪星的控制加速度。

由图1中相对运动关系可知

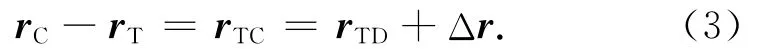
式（2）与式（1）相减，并根据式（3）的相对运动关系，可得目标星轨道坐标系中的相对运动方程

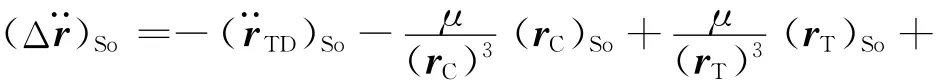
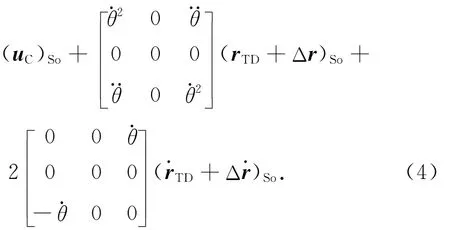
式（4）为完整的两星相对轨道动力学方程，在近圆轨道、近距离的条件下，按C－W方程的简化方法，可得近圆轨道的相对运动方程为

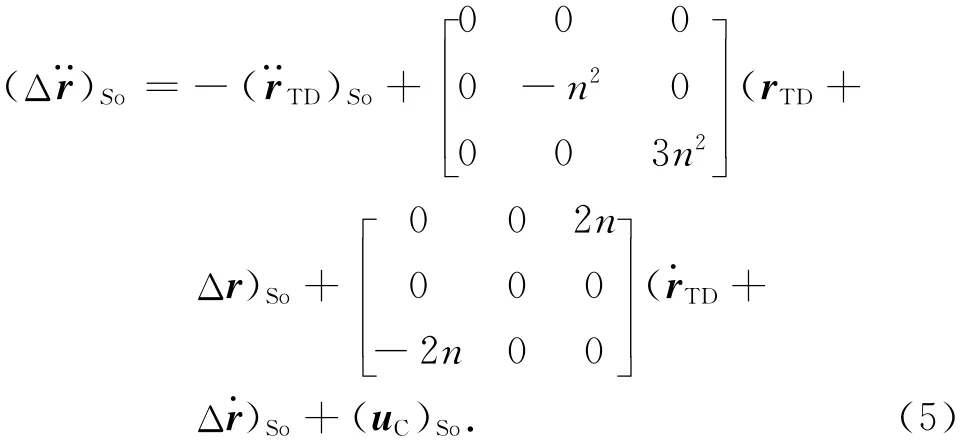
式中：n为目标星近圆轨道的轨道角速度［5］。令

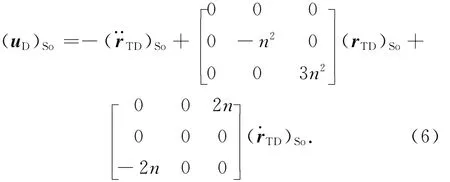
式中：uD为伴飞点相对目标星的相对状态引起的动力学方程中的常值项，可用前馈控制进行补偿。

将式（6）代入式（5），在轨道坐标系中展开后可得目标星自由飞行时的定点伴飞相对轨道动力学方程

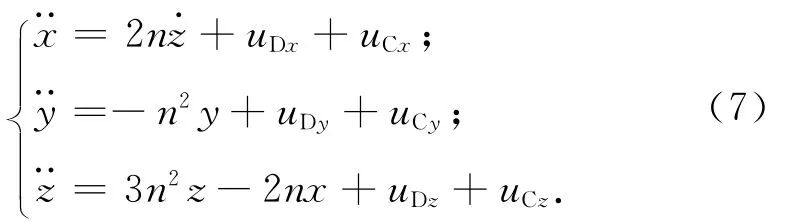
式中：x，y，z为Δr在轨道坐标系三轴的分量。

1.2 带不确定项的相对动力学

非合作目标进行轨道机动时，追踪星对其轨道推力的大小和方向均未知，可将其机动加速度作为一个未知的干扰量加入相对运动学方程，构成一不确定系统。该不确定系统可用状态方程表示为

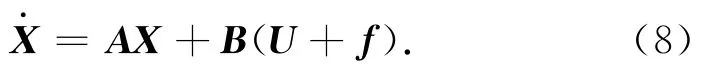
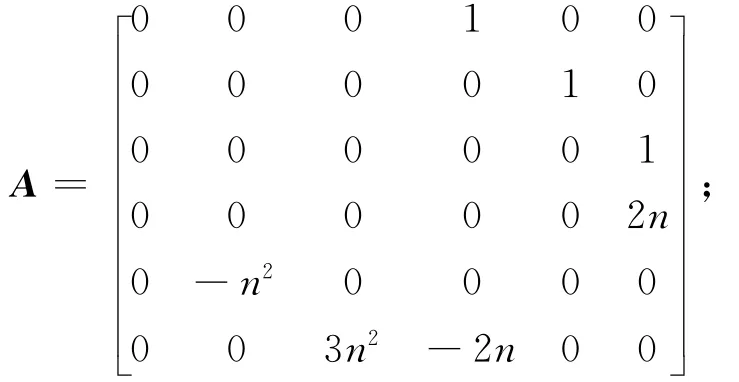
2 不确定系统的定点伴飞控制方法

2.1 目标不机动时的伴飞最优控制方法

若目标不机动，则式（8）中f为0，相对动力学方程是线性方程。设计控制律的目的是使追踪星相对目标伴飞点的相对状态X趋近于0。根据线性二次最优控制原理，定义性能指标为

式中：Q，R为正定矩阵［6］。

根据LQR理论，最小化性能指标的最优控制律为

式中：矩阵P为Riccati方程，式（11）的唯一正定解。

求出控制U后，可解出追踪星实际所需的uC。

2.2 针对不确定参数的控制律设计

目标星进行轨道机动后，追踪星需施加额外的控制力克服目标的未知机动力，保证定点伴飞。设额外的控制力为uL，结合目标不机动时的最优控制力，代入式（8），可得

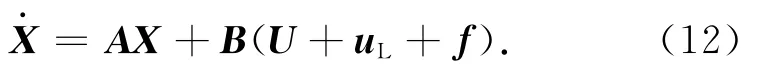
设计控制律，首先定义Lyapunov函数

式中：K为正定矩阵。

证明＜0，则系统渐进稳定，即追踪星相对伴飞点的相对状态X会趋近于零。对式（13）求导，并结合式（10）、（12）后化简可得

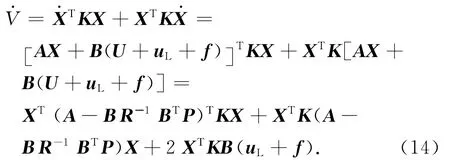
将最优控制律代入目标不机动时的相对轨道动力学方程中，可得

由于该系统渐进稳定，可得

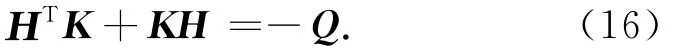
则代入式（14）中等号右边前两项后可推得

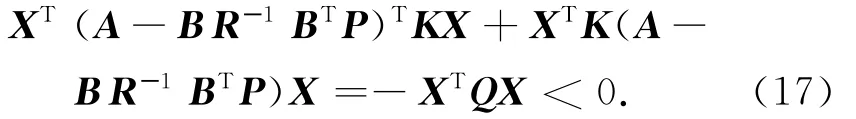
为保证不确定系统为渐进稳定，即＜0，只需证明2XTKB（uL＋f）≤0。

使用控制律

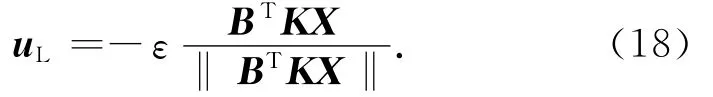
式中：参数ε≥‖f‖，可理解为追踪星的机动能力要大于目标星的机动能力。则

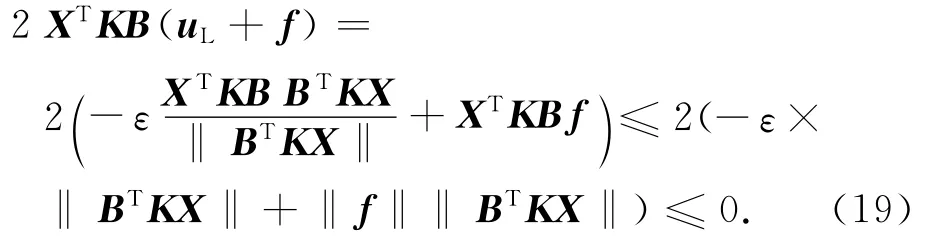
因此采用式（18）控制律时，条件2XTKB（uL＋f）≤0可满足，证明不确定系统渐近稳定。综合最优控制U，uL，可得出结论：欲使目标机动条件下的不确定相对动力学系统渐近稳定，追踪星实际所需的轨道控制加速度

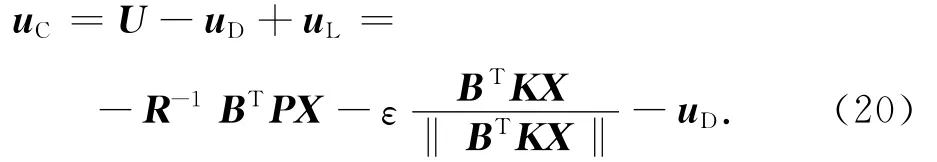
3 仿真

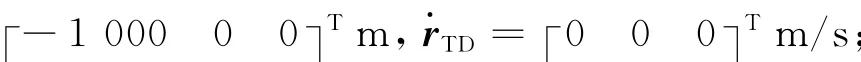
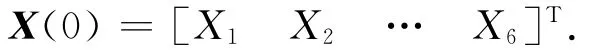
式中：X1＝－4 000m；X2＝－200m；X3＝200m；X4＝2m／s；X5＝0.5m／s；X6＝0.5m／s。

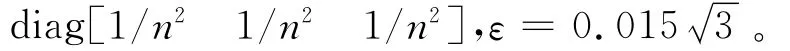
目标星三轴推力如图2所示。第一个轨道周期时推力器不工作，5 800s后，即从第二个轨道周期开始，目标星持续进行三轴机动。采用线性二次最优控制律的定点伴飞结果如图3所示，在目标星未机动时，追踪星由初始相对位置机动至伴飞点并能形成稳定伴飞。5 800s后目标机动，采用LQR控制律仍能形成定点伴飞，但伴飞的位置误差接近20m，伴飞效果受影响。

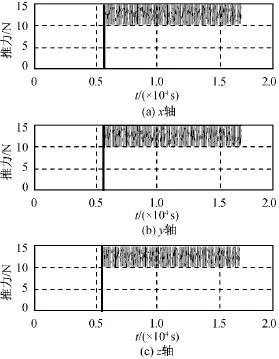
图2 目标星三轴推力Fig.2 Thrust in each axis of target satellite

采用目标机动控制律的定点伴飞全过程相对位置和目标机动后目标位置的仿真结果如图4、5所示。目标机动后采用相应的针对不确定系统设计的控制律，可使定点伴飞的精度维持在1m左右，较采用LQR控制律高出一个量级，可确保在目标机动时仍能为执行定点侦查、跟踪等任务提供有力条件。

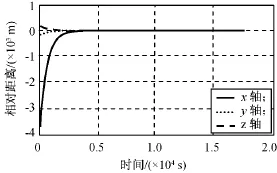
图3 采用LQR控制律的定点伴飞相对位置Fig.3 Relative position of station keeping control under LQR control law

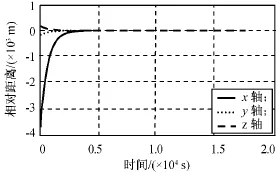
图4 采用目标机动控制律的定点伴飞相对位置Fig.4 Relative position of station keeping control under uncertain system control law

图5 机动时的定点伴飞位置精度Fig.5 Station－keeping precision

为考察不确定系统控制方法的鲁棒性，对第二种目标机动进行仿真。目标星在第一轨运行期间保持自由飞行的状态，第二轨开始目标星进行三轴机动，三轴推力器输出为常值13N，追踪星采用目标机动时的控制律继续进行定点伴飞，并保持2个轨道周期。仿真其余参数和伴飞要求与上述第一种仿真相同。

定点伴飞相对位置仿真结果如图6、7所示。由图可知：目标星采取不同的机动策略，追踪星采用不确定系统控制方法仍可实现对目标的稳定伴飞，且伴飞精度仍然维持在1m的量级，证明该方法对目标不同的机动有较强的鲁棒性。

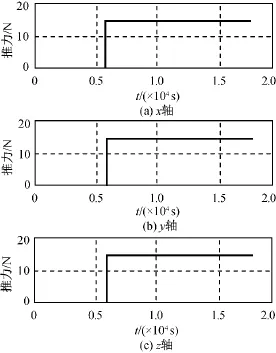
图6 第二种情况下的目标星三轴推力Fig.6 Thrust in each axis of target satellite in case 2

4 结束语

本文以机动目标的定点伴飞任务为研究背景，带不确定项的定点伴飞相对轨道动力学模型为研究对象，用LQR法设计目标自由飞行时的伴飞最优控制律，针对不确定系统，引入Lyapunov法，通过两种方法综合设计适用于目标机动条件下的定点伴飞的控制律。仿真结果表明：该控制律确保在不能获知精确目标机动加速度时仍可实现精确伴飞，而且对不同的目标机动具有较强的鲁棒性。

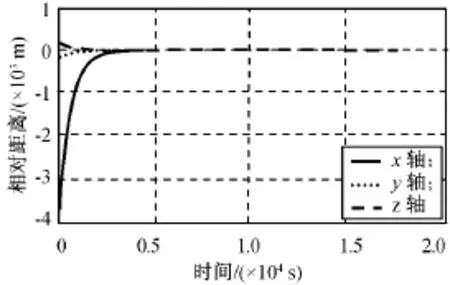
图7 采用目标机动控制律的定点伴飞相对位置Fig.7 Relative position of station keeping control under uncertain system control law

［1］ 林来兴.空间交会对接技术［M］.北京：国防工业出版社，1995.

［2］ 崔乃刚，王 平，郭继峰，等.空间在轨服务技术发展综述［J］.宇航学报，2007，28（4）：33－39.

［3］ ZIMPFER D，KACHMAR P，TUOHY S.Autonomous rendezvous，capture and in－space assembly：past，present and future［R］.AIAA，2005－2523.

［4］ 卢 山，徐世杰.非合作目标的自主接近控制律研究［J］.中国空间科学技术，2008，28（5）：7－12.

［5］ CLOHESSY W H，WILTSHIRE R S.Terminal guidance system for satellite rendezvous［J］.Journal of the Aerospace Science，1960，27（9）：653－658.

［6］ 李国勇，张翠平，郭红戈，等.最优控制理论及参数优化［M］.北京：国防工业出版社，2006.