基于单元串联的无速度传感器矢量控制算法研究
黄 哲,惠浩浩,韩龙飞,沈传文
(西安交通大学 电气工程学院,陕西 西安 710000)
引言
高压变频调速技术具有功率因数高、调速性能好、节能效果明显等优点,而单元串联多电平因其有着输出电压波形好和可靠性高等优点成为了高压变频器的主流方案,但目前无速度传感器矢量控制的高压变频器普遍存在低速性能不佳等问题,如何扩宽调速范围和提高系统性能具有非常高的研究价值[1]。
在无速度传感器矢量控制系统中,电机转速的估测尤为重要,而目前广泛应用的以电机的电压模型及其电势计算为基准的方法导致了无速度传感器矢量控制系统的低速性能不理想[2],关于电机低速稳定运行方面,大量文献给出了提高交流电机无速度传感器矢量控制系统低速控制性能的若干解决方案,但至今还没有一种为大家所承认的标准的无速度传感器矢量控制系统。文献[3]提出了一种具有转矩型MRAS,设计了一个与转子时间常数相匹配的滞后电路,减小电机参数尤其是定子电阻的影响,并给出了电机运行在18 r/min时的实验结果,但这种算法比较复杂且需要额外的电路。文献[4]描述了一种基于EKF的感应电机矢量控制和直接转矩控制系统,但是转动惯量和电阻值需要使用测量值,低速实验表明,估测转速的误差在10%左右。文献[5]提出了一种改进型的电机定子磁链定向直接矢量控制系统,定子磁链采用闭环估计,转速通过MRAS方法进行估测,并给出了仿真结果和轻载实验结果,空载低速运行时,估测转速和实际转速基本一致,50%负载低速运行时,实际转速为4 r/min,估测转速为7 r/min,误差较大。文献[6]试图通过对磁通观测器添加激励信号来改善在零频或极低速时转速辨识不稳定的问题,实验结果显示,零频时,激励信号为零,反电动势很小,定子电阻变化或者测量误差,这种算法理论上并不能解决低速问题。文献[7]利用限幅反馈的方法估测电机转子磁链,通过神经元自适应的转速辨识算法,完成无速度传感器矢量控制,并对带0.5倍额定载启动进行了实验,结果显示估测转速波动较大,波动的原因主要是采样和计算过程中受到干扰和离散误差的影响。文献[8]指出了传统的MRAS算法容易受到采样电压电流直流偏移的影响,低速阶段的稳定性较差,文中提出了一种改进型的MRAS算法,参考模型采用改进型转子磁链电压模型,电流模型作为可调模型,实验证明电机空载启动时转速辨识精度较好,但并未给出带载启动时的情况。
本文将基于定子电流的MRAS速度估测算法应用到单元串联高压变频器无速度传感器矢量控制系统,这种算法比较简单且具有良好的转速辨识准确度,从而使系统有了良好的动静态性能,并且在低速性能方面表现优越。
1 基于定子电流的MRAS方法
基于定子电流的MRAS速度估测算法直接采用异步电机本身作为参考模型,参考变量都是可以通过电机直接测得的输出量;用含有转速信息的电流模型和定子模型共同作为可调模型,这样,参考模型和可调模型的输出经过合适的模型参考自适应算法就可以获得转速信息。
电机的输入是三相定子电压,输出是电机转速和三相定子电流。因为电机转速是待观测量,所以用电流矢量作为参考变量。电机定子模型的数学模型如下式所示,通过电机定子模型可以获得定子电流矢量的观测值

式中:us为定子电压;为电流矢量观测值;为磁链矢量;为转速估测值;rs为定子电阻;rr为转子电阻;xs为定子漏抗;xr为转子漏抗;xm为励磁电抗;为漏磁系数;TN=1/2fsN,fsN为额定频率。
通过上式可以看出,计算定子电流的观测值需要用到磁链矢量观测值,因为电压模型在低速时存在问题,这里选择电流模型来计算磁链矢量观测值,计算公式如下:
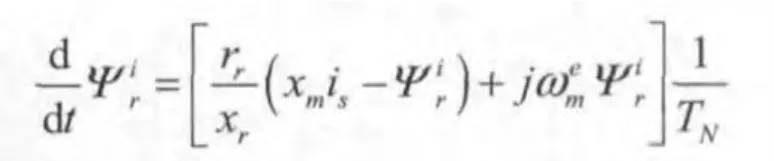
在计算过程中,所有的矢量在两相静止坐标系的分量上分别进行计算。
记定子电流的实际值与估测值之差Δis和磁链矢量的叉积为电机转矩的实际值和观测值之差,电机转矩的实际值和观测值之差通过合适的自适应环节就可以获得电机转速的估测值,计算公式如下:
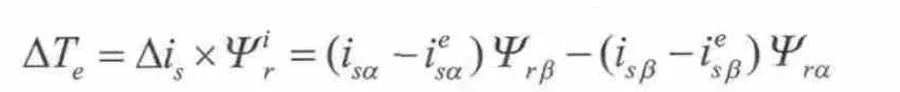
自适应调节算法依然采用PI调节器控制,转子转速辨识公式为:

基于定子电流的MRAS算法的框图如图1所示。
这种算法利用电动机本身可以直接测得的量作为参考模型,消除了电压模型存在的纯积分及对参数鲁棒性差等问题,模型中的参数都是可以从电机上直接测量获得的,具有较好的参数鲁棒性和优

图1 基于定子电流的MRAS框图
2 仿真结果及分析
秀的动态性能。
为验证基于定子电流的MRAS方法具有良好的性能,采用Matlab/Simulink对异步电机基于定子电流的MRAS速度估测算法进行了仿真,其仿真模型如图2所示,仿真所用的异步电机的参数为:额定电压380 V,额定功率4 330 W,额定转速1 500 r/min,极对数2,定子电阻1.812 9 Ω,定子电感0.012 13 H,转子电阻1.91 Ω,转子电感0.012 13 H,互感 0.314 5 H,转动惯量 0.02 kg·m2,摩擦系数0.005 752 N·m·s。
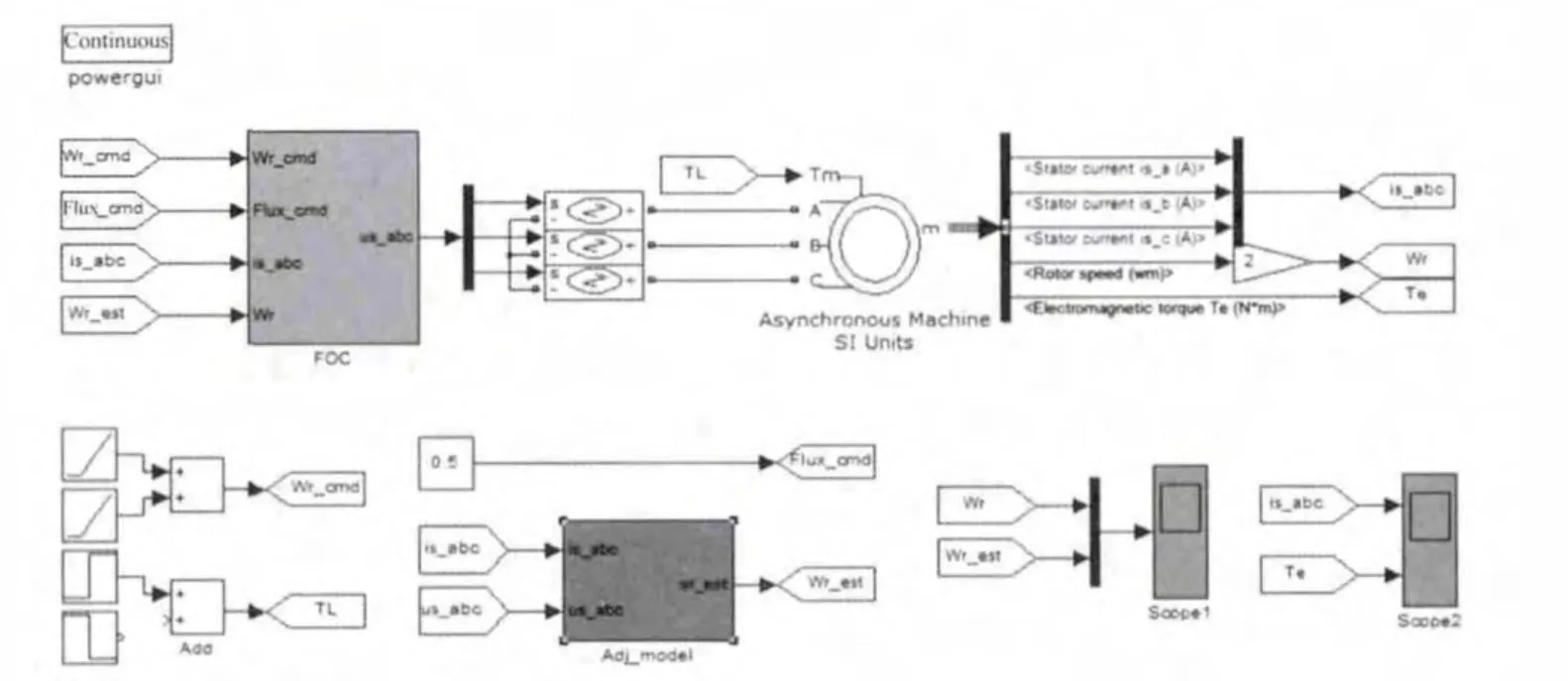
图2 基于定子电流的MRAS仿真模块
电机的给定速度为斜坡曲线,电机运行稳定后,在0.8 s时突加40 N·m的负载,在1.2 s时卸掉负载。仿真结果如图3所示。
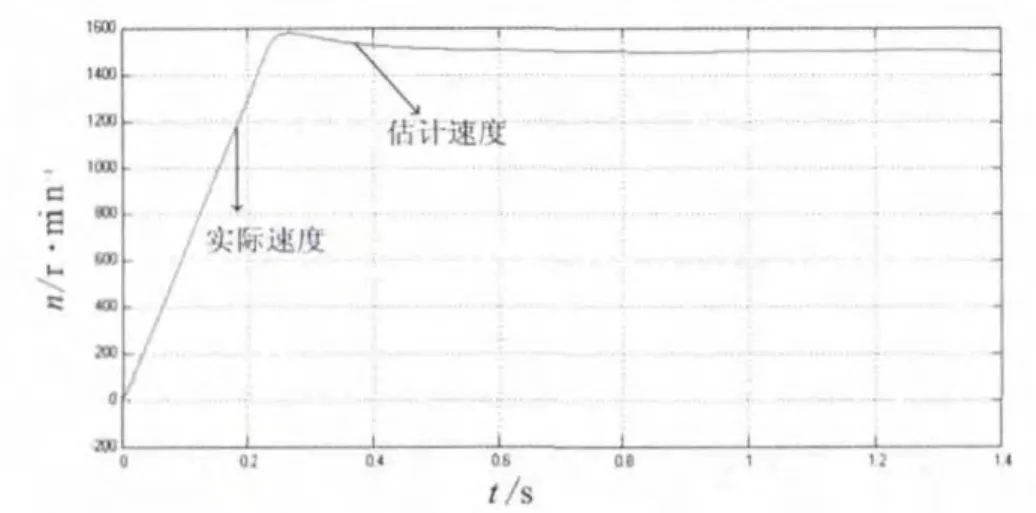
图3 基于定子电流的MRAS仿真结果
通过仿真结果可以看出,电机在启动瞬间,估测转速稍有滞后,但在很短的时间内就能跟踪上实际转速,估计转速曲线和实际转速曲线基本重合,误差非常小。加减载过程中,估测转速几乎没有波动,始终跟踪实际转速。
图4 为定子电流α轴和β轴实际值和观测值仿真结果,对于这种算法来说,定子电流的观测值是计算估测转速的一个非常重要的中间量,其准确与否也直接影响到转速估测的精度,对于本设计具有至关重要的作用。从图中可以看出,定子电流的实际值曲线和估测值曲线具有很高的吻合度。

图4 定子电流实际值和观测值仿真波形
和电机定子电流一样,转子磁链也参与到转速估测的计算中,转子磁链的d轴和q轴仿真波形如图5所示。
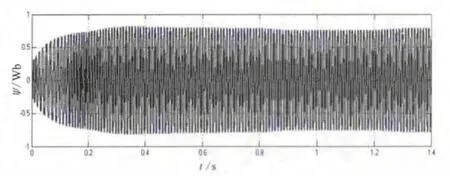
图5 转子磁链仿真波形
图6 为定子电流励磁分量id和转矩分量iq的仿真波形,id的值在磁场建立完成以后恢复到初始值0,且不再发生变化;iq的值在电机完成加速过程稳定后恢复到初始值0,加减载时跟随负载发生变化,可见定子电流转矩分量和励磁分量实现解耦。
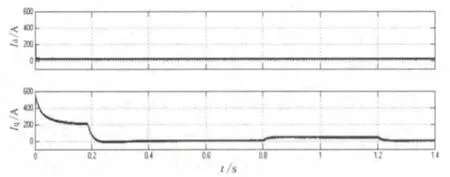
图6 定子电流励磁分量和转矩分量仿真波形
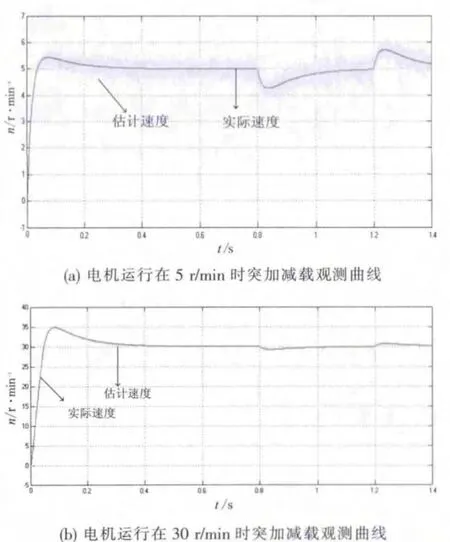
图7 电机低速突加减载仿真波形图
另外,为了测试这种算法在低速时的表现,重点对系统的低速性能进行仿真验证。图7为电机运行在5 r/min和30 r/min时突加减载的波形图,同样在0.8 s时突加40 N·m的负载,在1.2 s时卸掉负载。
如图7(a)所示,电机启动时和稳定运行在5 r/min时突加减载瞬间,估测转速的误差控制在10%以内,估测转速准确随实际转速,但有一定的波动,定子电流采样在低速时有一定的误差是造成这种现象的原因之一,由于电机的惯性作用使得小范围的波动不会对系统的稳定造成影响。如图7(b)所示,电机运行在30 r/min时,估测转速的误差控制在2%以内且基本没有波动,无论在电机启动阶段还是突加减载时,估测转速能够在较短时间内完成调整,具有较好的动态性能。
通过上述各仿真结果可以发现,基于定子电流的MRAS的转速辨识模型通过电机本身可以实时测得的参数进行运算,避免了其他参数的变化对转速辨识结果的影响,并且这种算法在低速阶段有良好的估测精度。
3 实验验证
3.1 硬件实验平台
本文根据单元串联高压变频器控制系统的拓扑结构和控制原理[10,11],搭建了硬件实验平台。由于现场环境及实验条件的限制,在保证实验系统的结构与真实系统完全相同的前提下,在设计中用380 V的进线输入电压代替6 kV或10 kV的进线电压,实验系统的结构组成如图8所示。
硬件实验平台主要包括:移相变压器、功率单元柜、主控箱、触摸屏、三相感应电机和磁粉制动器等。
感应电机为380 V/7.5 kW三相异步电机,定子绕组采用星形连接方式,额定负载为1.8 N·m。功率单元柜分为三个小单元柜,每个小单元柜放置了5个功率单元箱,功率单元柜最右边为控制柜,包含主控箱、PLC、继电器和电气开关等。移相变压器的输入为380 V交流电,输出为15路,输入端为星型联结,副边采用延边三角形的方式联结,移相角为12±0.2°,容量为50 kVA。磁粉制动器其能提供的最大负载转矩为200 N·m。
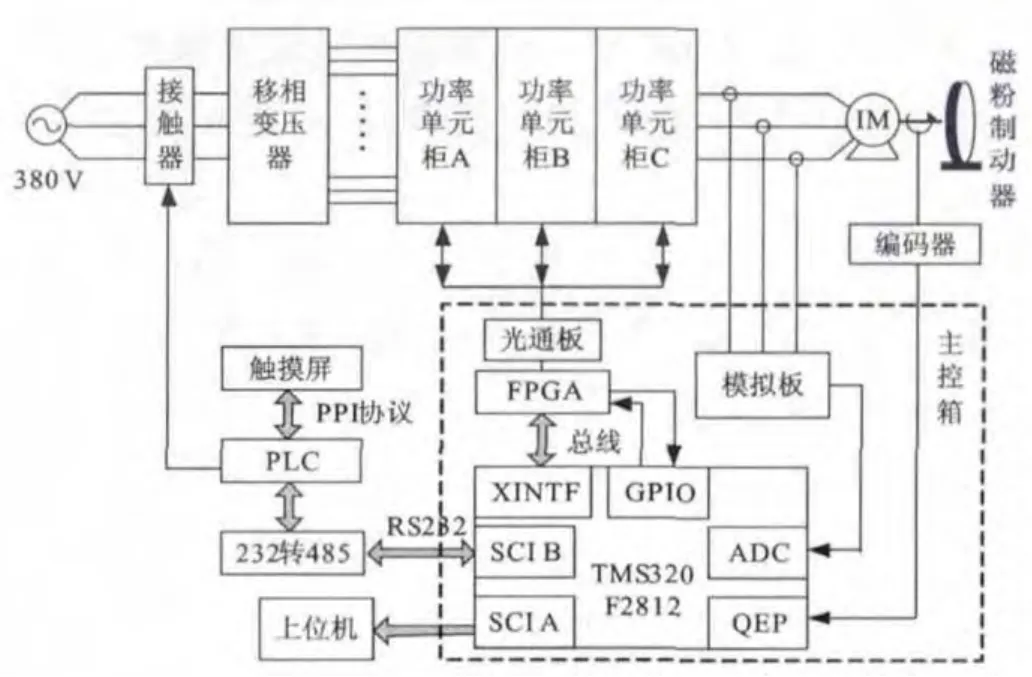
图8 实验系统结构组成框图
3.2 实验结果分析
(1)空载启动实验
空载启动运行实验中,设定转速500 r/min,通过主控测试软件和示波器对各主要观测量进行观测,主要对电机实际转速和估测转速进行对比,并且观察算法对于定子电流估测的准确度,主要变量观测曲线和波形如图9所示。
可以看出,电机启动瞬间,估测转速能够完全跟踪电机的实际转速,在转速进入稳态的瞬间,几乎没有超调量。在低速阶段,估测转速与实际转速误差在3%以内。一方面说明转速调节器的PI参数的选取比较合适,另一方面说明基于定子电流的MRAS速度估测算法的效果较为理想。定子电流的估测曲线和实际曲线基本重合,转子磁通观测波形正弦度较好。另外,实验中对定子电阻和转子电阻进行了变化范围为20%的鲁棒性实验,调速系统依然稳定,且转速误差小于10%,说明这种算法对电机部分参数的鲁棒性较好。由此说明,电机在空载情况下的启动实验是符合设计要求的。
(2)1.5倍额定负载启动实验
实验所采用电机的额定负载为18 N·m,1.5倍额定负载启动是对电机低速性能的一个考验。电机1.5倍额定负载启动时,用主控测试软件对各主要观测量进行实时观测,观测波形图如图10所示。其中图10(a)是电机定子电流励磁分量和转矩分量的观测波形图,图10(b)为电机估计转速曲线与实际转速曲线的对比,图10(c)为电机启动稳定后相电压和相电流波形图。
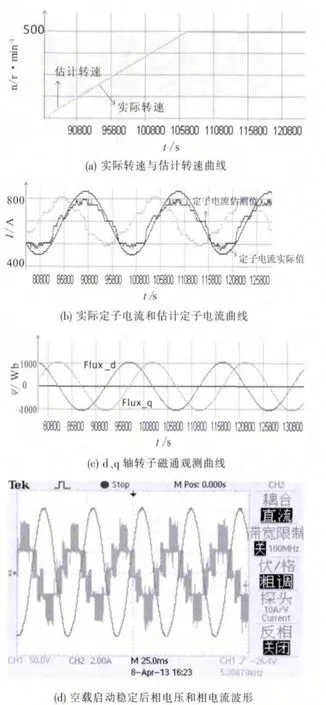
图9 空载启动各观测量曲线
如图10(a)所示,电机启动时,定子电流转矩分量iq的值瞬间增大,而励磁分量id的值保持不变,实验结果表明,id和iq实现解耦。等到电机进入稳态后,iq的值也趋于稳定。
通过图10(b)电机的估测转速和实际转速进行对比,电机等待启动阶段,估测转速和实际转速有少许的误差。电机开始转动后,估测转速能够迅速的跟踪上实际转速,瞬时速度偏差接近零,可见这种速度的动态性能良好。通过图10(c)可以看到,带载启动后相电流的幅值明显增大,相电压阶梯状明显,毛刺较少,波形正弦度良好。

图10 电机1.5倍额定载启动时各观测量曲线
(3)堵转启动实验
电机的堵转启动实验是否达到要求是验证电机低速性能的重要参考,这种极端工作状态也对电机的低速性能提出了非常高的要求。堵转启动实验的具体步骤如下:电机启动前,给电机加三倍的额定负载,然后启动电机,使电机堵转,然后减掉负载,测试电机是否能够正常启动并且不发生过流报警。各主要观测量的波形图如图11所示。
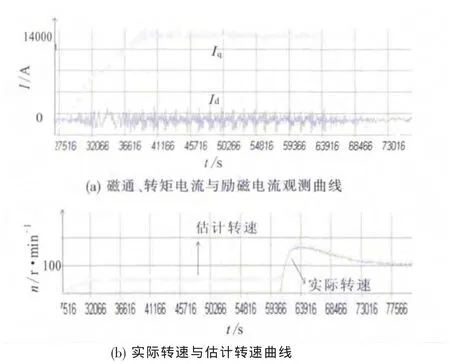
图11 电机堵转启动时各观测量曲线
由图11(a)可以看出,电机在堵转过程中,定子电流转矩分量迅速增大到最大值并维持恒定,减载后迅速降为初始状态,整个过程中,定子电流励磁分量几乎没有变化。图11(b)为电机估测转速和实际转速的对比,堵转过程中,估测转速有少许的偏差。零速运行一段时间后减掉减载,电机开始转动,估测转速依然能够迅速跟踪上实际转速。整个过程中,系统未出现过流报警,这种对于电机工作在极端状态的实验,有效的说明了电机具有良好的低速性能。
(4)突加减载实验
突加减载实验是为了测试电机在负载突变时的动态性能,当电机分别在30 r/min(1Hz)、150 r/min(5Hz)、300 r/min(10Hz)、600 r/min(20Hz)、1500 r/min(50Hz)稳定运行时,使用磁粉制动器对其突加1.5倍额定负载,并在系统稳定后减去负载。各频率段突加减载时主要观测量的波形图如图12所示,其中绿色曲线为实际转速,黄色曲线为估测转速。
经过对电机空载启动、带载启动、堵转启动和各频率段突加减载实验,初步证明基于定子电流的MRAS方案满足无速度传感器矢量控制对转速辨识准确度、参数鲁棒性和动静态性能的要求;实验过程中,通过采用改进型转子磁链观测器,并设计了转子磁链相位角的补偿算法,实现了转子磁链的准确估测。经过一系列的改进和调试,该无速度传感器矢量控制系统具备以下性能:

图12 各频率段突加减载时主要观测量
(1)系统在空载状态下运行良好,加减速时运行平稳,估计转速误差控制在2%以内,转速最低可准确辨识到1 Hz,控制精度达到同等产品较高水平;在极低速方面,可在0 Hz附近稳定运行,转速可控制在10 r/min,基本满足一般工艺要求的最低频率要求;
(2)电机在1.5倍额定负载的情况下启动时,电机运行平稳,估计转速能够迅速跟踪上实际转速,和空载运行时的电流相比,电流输出的幅值明显增大,电压输出波形的阶梯数增加,电压电流波形良好;
(3)电机在堵转启动时没有出现过流报警现象,卸载后电机平稳启动,估计转速迅速跟踪上实际转速,具有较好的启动性能和低速(零速)性能,可见系统可以满足复杂恶劣的应用环境;
(4)在对电机运行在各速度段进行加减载实验中,突加减载瞬间,电机的实际转速和估计转速有微小的波动,波动范围大概为±10 r/min以内,在其他时间段可完全根据给定速度运行,且在波动瞬间,估计转速仍然能够实现对实际转速的跟踪,表明基于定子电流的MRAS的转速辨识算法的可行性,系统在中高速阶段同样具有较好的动静态性能。
4 结论
本文中单元串联高压变频器无速度传感器矢量控制系统采用了基于定子电流的MRAS速度估测算法,这种算法具有良好的转速辨识准确度并且对电机参数鲁棒性较好,使系统具有良好的动静态性能并大大提高了系统的低速性能。实验结果证实了电机无论是空载启动,带载启动,堵转启动,还是各频率段的突然加减载,其估计转速都能较准确地跟踪实际转速,说明了该算法的可行性。
[1]徐甫荣,陈辉明.高压变频调速技术应用现状与发展趋势[J].深圳:变频器世界,2006(4):61-67.
[2]周有为,刘和平,刘述喜.异步电机无速度传感器矢量控制[J].电机与控制应用,2005(3):52-54.
[3]T Ohtani,N Takada,K Tanaka.Vector control of induction motor without shaft encoder[J].IEEE Transactions onIndustry Applications,1989,28(1):157-164.
[4]Barut M,Bogosyan S,Gokasan M.Speed-sensorless estimation for Induction Motors using extended Kalman filters[J].IEEE Transactions on Industrial Electronics,2007,54(1):272-280.
[5]Mitronikas E D,Safacas A N.An improved Sensorless Vector control method for an Induction Motor Drive[J].IEEE Transactions on Industrial Electronics,2005,52(6):1660-1668.
[6]Yamaguchi N,Hasegawa M.A stabilization method for speed sensorless vector controlled induction motors at zero frequency operating condition with multirate adapive observer[C].30th Annual Conference of IEEE Industrial Electronics Society,Busan,South Korea:2004.
[7]陈冰,冬雷,杨栋.低速下异步电机无速度传感器矢量控制研究[J].西安:西北大学学报,2007,37(1):45-48.
[8]杨奇,张裕峰,胡炫,钱诗宝.高压变频器无速度传感器矢量控制转速辨识[J].电力电子技术,2012,46(8):97-99.
[9]TeresaOrlowska-kowalska.Stator-Current-Based MRAS estimator for a wide range speed-sensorless Induction-Motor drive[J].IEEE Transactions on Industrial Electronics,2010,57(4):1296-1308.
[10]竺伟,陈伯时,周鹤良,赵相宾.单元串联多电平高压变频器的起源、现状和展望[J].电气传动,2006,36(6):3-4.
[11]周京华.多电平逆变器拓扑结构及调制策略的研究[D].西安:西安交通大学,2005.

