逆变器无线并联虚拟阻抗分析

路嘉鑫 ，张颖超，钱希森 ，程 松 ，赵争鸣

（1.重庆通信学院，重庆 4000352；2.清华大学电力系统国家重点实验室，北京 100084）

引言

现代电源供电系统由传统集中式供电向分布式供电发展，高频模块化UPS的出现大幅提高了系统的可靠性和扩展能力。如何实现并联模块间均流，成为了高频模块化UPS的关键技术之一[1]。近年来国内外学者围绕该问题开展了大量的研究，其中逆变器无线并联控制取消了传统逆变器并联控制中模块间的互联线，成为未来模块化UPS并联控制的研究热点和发展方向[2]。

逆变器无线并联控制的核心思想为PQ下垂控制，该控制策略源于交流发电系统中，当系统输出功率增加时通过降低发电机输出频率实现并联发电机间均流。逆变器无线并联控制利用逆变器输出有功无功与输出电压频率幅值间的耦合关系，通过下垂控制实现逆变模块间的均流。由于模块只需检测自身输出电压信息就能生成控制信号，实现了模块“自治”[3]。

传统PQ下垂控制是从逆变器并联理想模型得出的，该模型各逆变模块参数完全一致，输出阻抗为纯感性且大小相等[4]。实际系统中由于器件参数以及输出线路阻抗不一致，导致各并联模块等效输出阻抗不同，而PQ下垂控制对输出阻抗性质极为敏感，造成并联模块均流不理想，形成环流[5]。本文在分析逆变器闭环系统输出阻抗性质和大小的基础上，通过加入虚拟阻抗使逆变器闭环系统输出阻抗呈感性，采用下垂控制策略，实现模块间的均流。

1 输出阻抗对下垂控制策略的影响

单台逆变器等效电路如图1所示：

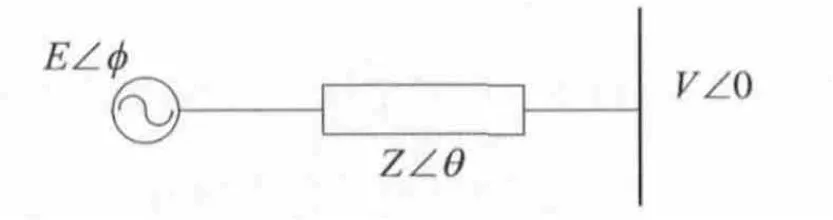
图1 单台逆变器等效电路

图中：E∠φ为逆变器等效电压源，V∠0为交流母线电压，Z∠θ为系统等效输出阻抗，设总输出功率S=P+jQ，计算可以得到：

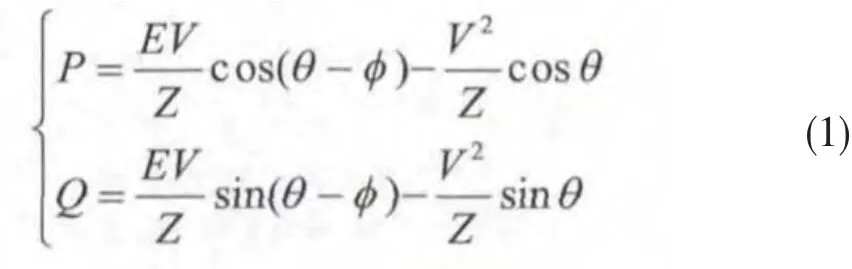
1.1 输出阻抗为纯阻性

输出阻抗为纯阻性时(Z=R),(1)式可简化为：

根据反馈控制，得到控制方程为：

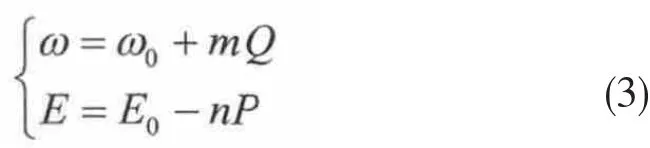
1.2 输出阻抗为纯感性

输出阻抗为纯感性时(Z=jX),(1)式可简化为：

根据反馈控制，得到控制方程为：

由式(3)和(5)可以看出，系统下垂控制策略对输出阻抗的性质极为敏感。参考电气工程手册可知，在低压配电网中，由于逆变模块间距近、线路横截面积小，线路阻抗特性呈阻性[6]。因此实际线路包含阻性导线和感性滤波电感部分，等效输出阻抗性质很难确定，所以在系统设计时应充分考虑输出阻抗对下垂控制策略的影响，适当选取下垂控制策略，满足等效内阻抗与下垂控制策略间耦合关系，实现均流[7]。

2 虚拟组抗法

2.1 逆变器等效输出内阻抗分析

为使逆变器输出电压能更好更快的跟踪参考电压，本文采用电流内环电压外环双环控制[8]，控制框图如图2所示：

其中Kpv、Kiv分别为电压外环比例、积分系数，Kp为电感电流内环比例系数，K1、K2分别为电感电流、输出电压采样系数，计算得到系统等效内阻抗传函：

图2 逆变器电流内环电压外环双环控制框图

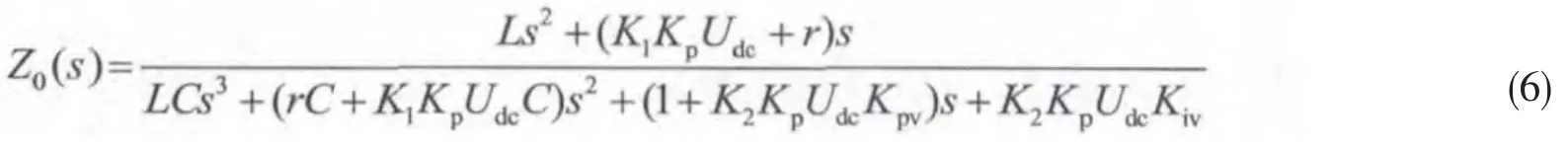
从式(6)可以看出，系统的等效内阻抗与器件参数和控制系数有关。为验证该结论，以Kiv变化对系统等效内阻抗影响为例，保持Kpv=5、Kp=1.2，分别令Kiv=0、100、300，得到的 bode图如图 3 所示：

图3 Kiv变化对系统等效内阻抗影响示意图

从图3可以看出，系统等效内阻抗受控制参数Kiv影响，随着Kiv从0增至300，等效内阻抗特性在低频段从阻性变为感性，实际系统中由于不同模块器件参数和控制系数不一致，势必会造成模块间等效内阻抗不一致，进而形成环流。

为抑制实际系统中并联模块间的环流，人们曾提出在逆变模块输出端串联耦合大电感以抑制瞬间环流，同时保证输出阻抗呈感性，确保下垂法的应用[9]。该方法实现了对模块间环流的抑制，但串联大电感体积大、成本高，且造成不可忽视的功率损耗。而虚拟阻抗思想的出现为解决环流问题提供了一条途径。

2.2 虚拟阻抗

由式(3)和式(5)可知系统等效内阻抗为纯感性或纯阻性时采用的下垂控制策略控制方程不同。如果在系统加入控制环，将逆变器等效输出阻抗校正为近似纯感性或纯阻性，进一步满足等效内阻抗与下垂控制策略间耦合控制关系，更好地实现均流，减小模块间的环流，这就是虚拟阻抗的思想[10]。由于该方法通过反馈控制实现而非在系统中实际串联阻抗，因此称为虚拟阻抗法[11]。

2.2.1 虚拟阻抗对系统等效内阻抗的影响

虚拟阻抗法用前级PQ下垂法得到的参考电压v*ref减去输出电流i0与虚拟阻抗ZV（s）的乘积，所得差值作为新的逆变参考电压vref，其控制方程为：

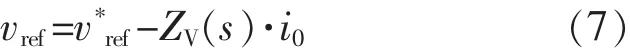
虚拟阻抗控制框图如图4所示：

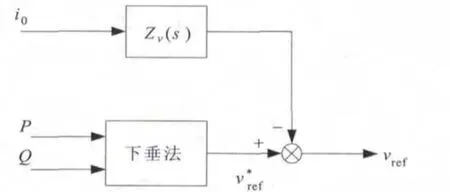
图4 虚拟阻抗控制框图

逆变器双环控制模型简化后得到单逆变模块等效电路如图5所示：

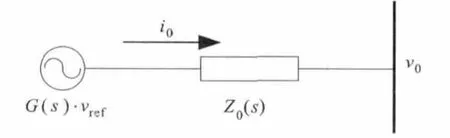
图5 单逆变模块等效电路

等效输出电压方程为：

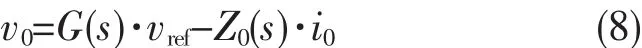
其中G(s)为电压增益，Z0(s)为系统等效输出阻抗。

将式(7)带入式(8)中可以得到

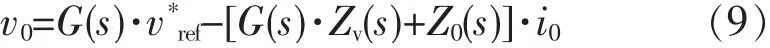
其中G(s)·Zv(s)+Z0(s)就是加入虚拟阻抗后系统等效输出阻抗，通过仿真可知：加入虚拟阻抗后系统等效输出阻抗性质取决于虚拟阻抗Zv(s)的性质，故系统设计时可先确定采用何种下垂控制策略，根据下垂控制策略选择虚拟阻抗性质。

2.2.1.1虚拟阻抗为阻性

当虚拟阻抗为阻性时(Zv(s)=R)，等效输出阻抗传函：

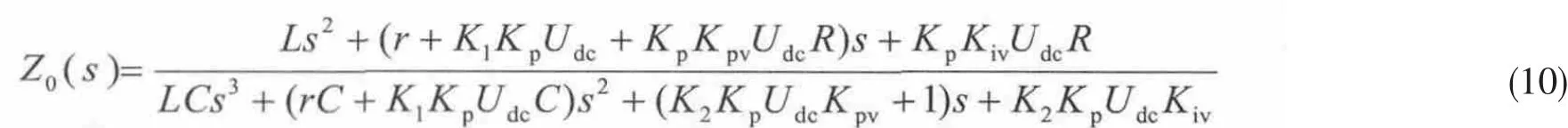
保持系统参数 kpv=5、kiv=100、kp=1.2、r=1， 将 Zv(s)=R=5e-3带入式 (10)中，并画出等效输出阻抗bode图如图6所示。

对比图6和图3可以看出，加入阻性虚拟阻抗后，系统等效输出阻抗较未加入虚拟阻抗，外特性更接近于纯阻性。

2.2.1.2虚拟阻抗为感性

当虚拟阻抗为感性时(Zv(s)=sLD)，等效输出阻抗传函：

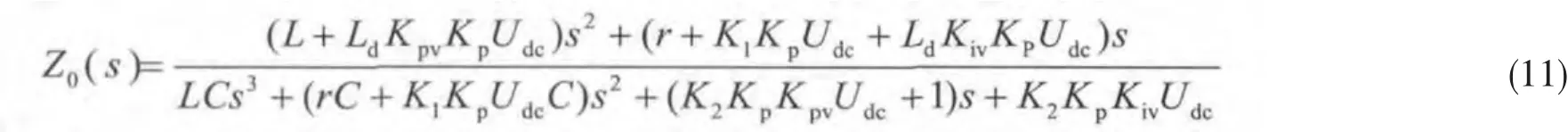
保持系统参数 kpv=5、kiv=100、kp=1.2、r=1， 将 Zv(s)=sLD=s(1e-3)带入式(11)中，并画出等效输出阻抗bode图如图7所示。

图6 虚拟阻抗为阻性时输出阻抗bode图

同上，加入感性虚拟阻抗后，系统等效输出阻抗较未加入虚拟阻抗，外特性更接近于纯感性。

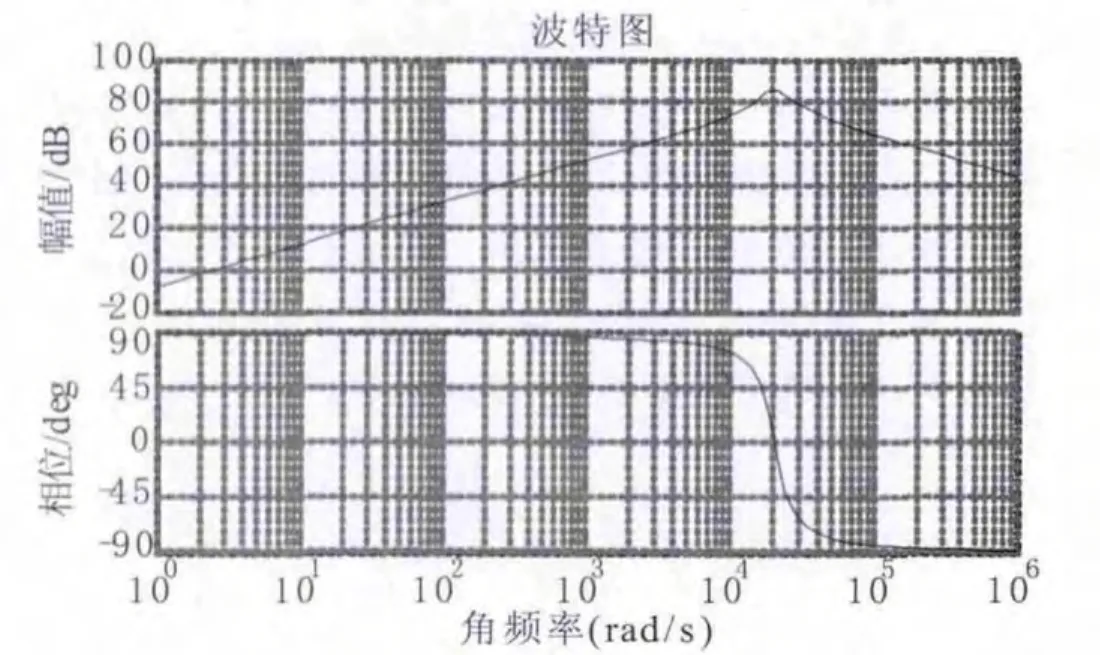
图7 虚拟阻抗为感性时输出阻抗bode图

对比图3与图6、图7可以看出：在加入虚拟阻抗之前，系统等效输出阻抗特性在低频段波动较大，这样的输出阻抗特性不利于下垂法控制方程的选择，导致模块间均流效果差；加入虚拟阻抗后，系统等效输出阻抗更接近纯感性或纯阻性，与下垂控制方程耦合度更高，更好地实现模块间均流。

2.2.1.3自校正虚拟阻抗

由于输出滤波电感的存在，一般情况下逆变器输出阻抗为感性，当系统带非线性负载时，高频谐波电流在等效输出阻抗上产生压降便不容忽视，导致输出电压畸变严重，THD很高，无法满足负载要求[12]。

为改善上述缺点，本文提出虚拟阻抗自校正法调节输出阻抗特性，使逆变器等效输出阻抗在输出电压的基波频段呈感性，在谐波频段呈阻性。通过使用如下虚拟阻抗实现：

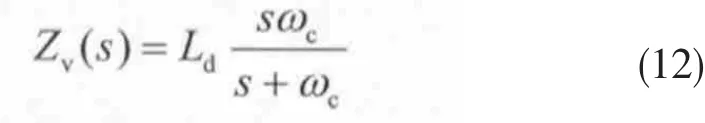
加入自校正虚拟阻抗后，等效输出阻抗传函：

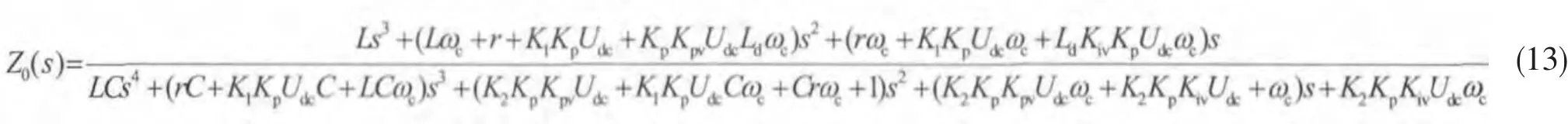
仿真得到 Ld=5e-3，ωc=100，200，300 Hz时逆变器输出阻抗波特图如图8所示：

图 8 Ld=5e-3，ωc=100，200，300 Hz 时逆变器输出阻抗波特图

从图8可以看出，加入自校正虚拟阻抗后，逆变器等效输出阻抗在输出电压的基波频段呈感性，符合等效阻抗与下垂控制策略的耦合关系，减小模块间环流；同时在谐波频段呈阻性，避免高频谐波电流在输出阻抗上压降过大，导致输出电压不满足负载需求。

2.2.2 虚拟阻抗对系统环流的影响

从上述分析可以看出，虚拟阻抗通过反馈控制实现了与直接在输出端串联阻抗等效的功能，解决了直接串联器件造成的体积大、成本高等问题，且不产生功率损耗，对减小系统环流具有积极作用。

两台逆变器并联等效电路如图9所示：

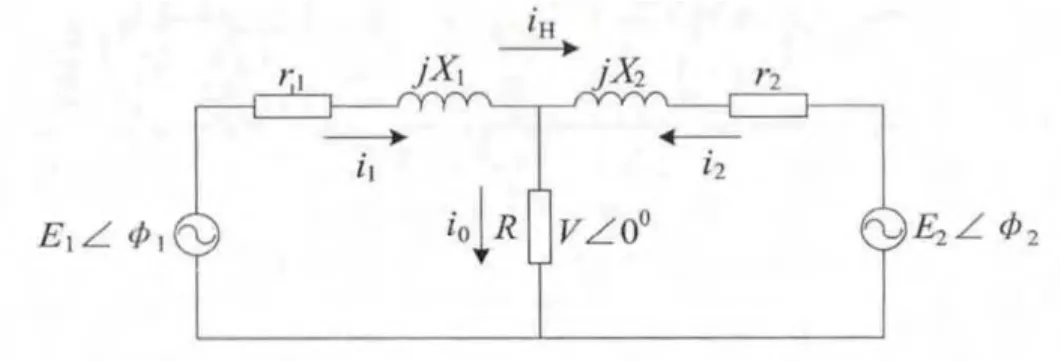
图9 两台逆变器并联等效电路

可以得到模块间环流为：

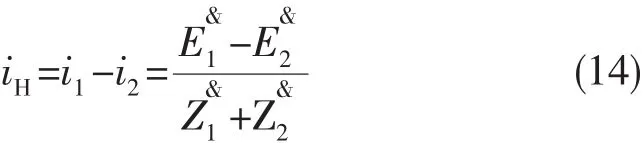
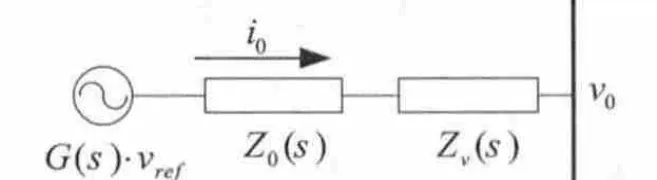
图10 加入虚拟阻抗后单逆变模块等效电路

从式(9)得到加入虚拟阻抗后系统的等效电路如图10所示。

可以得到加入虚拟阻抗后模块间环流为：

虚拟阻抗的加入可以抑制模块间环流，且由于不是实际加入元件，不会产生压降和能耗，这些都是虚拟阻抗的优点。但从式(9)也可以看出，由于虚拟阻抗的加入，参考输出电压会有一定下降，最终导致输出电压下降，因此虚拟阻抗法是以降低逆变器输出电压精度为代价实现减小模块间环流的。

3 仿真结果

在Matlab/Simulink环境下搭建两台10kVA逆变器并联仿真模型，在对系统等效输出阻抗分析后，选取合适下垂控制策略，并加入虚拟阻抗，仿真参数如表1所示：

表1 仿真参数

图11 所示为系统带非线性负载时，逆变器输出电压v0、参考电压vref、单逆变器输出电流i0波形：

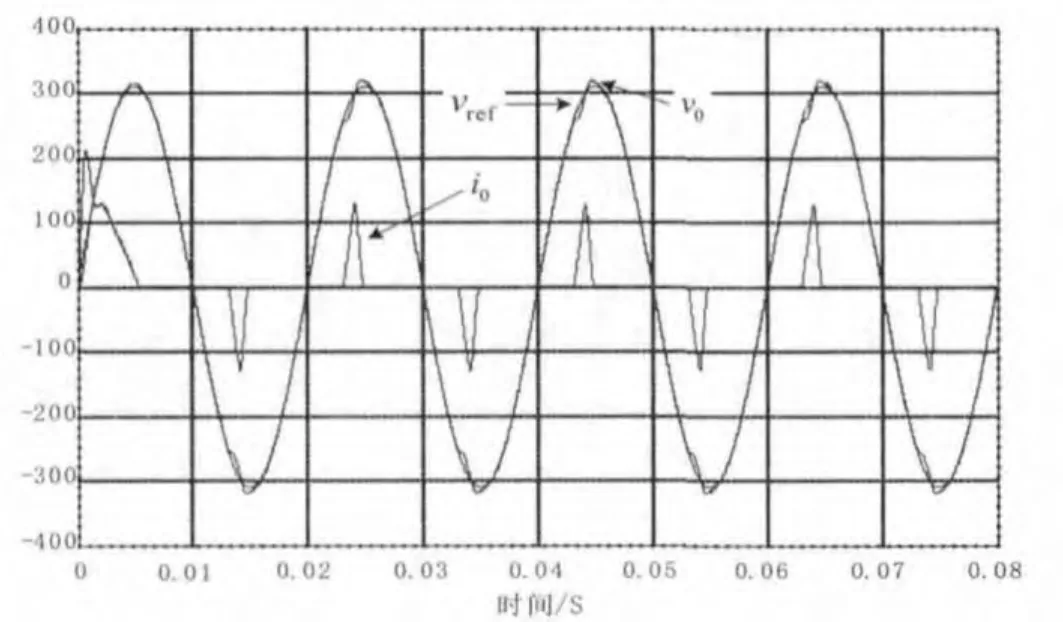
图 11 带非线性负载时 v0、vref、i0波形

从图11可以看出，系统带非线性负载时，输出电压波形正弦度高，THD=2.33%，同时由于系统使用了双环控制，输出电压波形较好的跟随了参考电压波形。

如图12所示为系统由半载到满载，再由满载到半载切换过程中逆变器1输出电流。

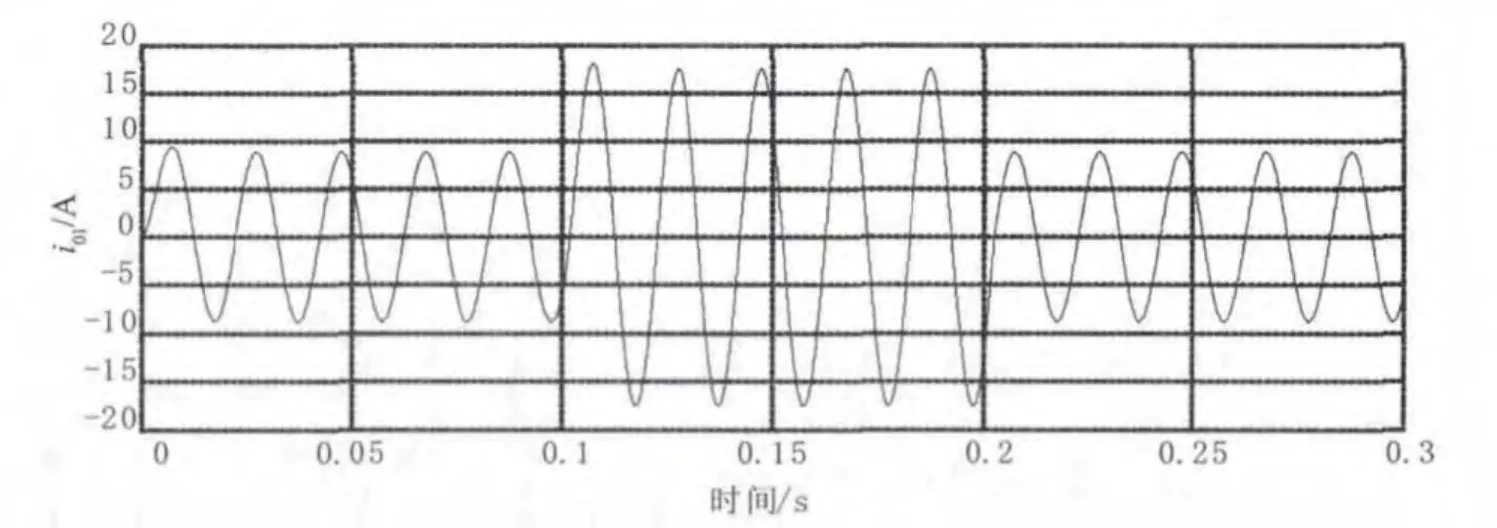
图12 系统负载切换过程中逆变器1输出电流

从图12可以看出，在逆变器无线并联控制下，在负载切换过程中系统稳定。

图 13 所示为 Z1=2+j1.36×10-3，Z2=0.78+j1.34×10-3时（Zi为第i台逆变器输出阻抗值），加入虚拟阻抗环节前后，系统环流大小对比。

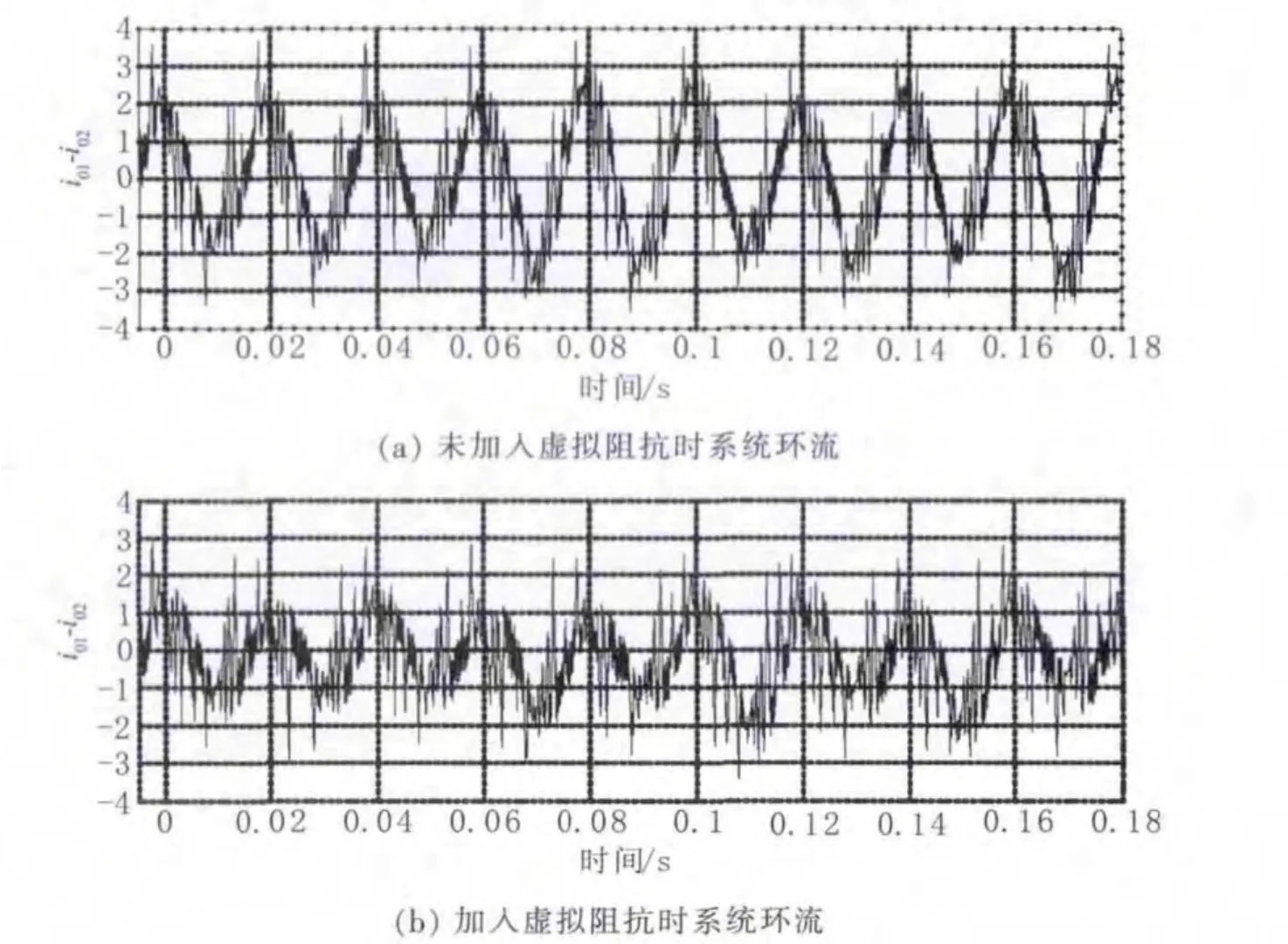
图13 加入虚拟阻抗前后系统环流对比

从图13可以看出，加入虚拟阻抗后，由于模块间参数不一致导致的环流相比加入前减小，同时更快的进入稳定状态，瞬态响应速度提高，验证了理论推导的正确性。

4 结论

模块化逆变器系统下垂控制策略对系统输出阻抗的性质极为敏感，需要充分考虑控制参数对等效内阻抗的影响，针对等效内阻抗性质采用对应的下垂控制策略，使其与等效内阻抗耦合，以更好地实现模块间均流。

虚拟阻抗通过控制策略实现校正系统等效输出阻抗性质，并抑制实际系统中由于系统器件参数分散性、输出连接线阻抗差异造成的模块间环流。本文就虚拟阻抗对系统等效内阻抗、系统环流的影响做了分析和仿真，验证了所得结论的正确性。

[1]阚加荣.单相逆变器无互联线并联控制技术研究[D].南京：南京航空航天大学，2007.

[2]E C Furtado， L A Aguirre， L A To赞rres.UPS parallel balanced operation without explicit estimation of reactive power—a simpler scheme[J].IEEE Transactions on Circuits and Systems， 2008：1061-1065.

[3]龙江涛，路嘉鑫，钱希森，等.UPS逆变器并联控制技术综述[J].电源学报，2013(5)：21-27.

[4]J M Guerrero， J Matas， L García de Vicun軌a， M Castilla.Wireless-Control Strategy for Parallel Operation of Distributed-Generation Inverters[J].IEEE Trans Ind Electron，2006，(53)：1461-1470.

[5]于玮，徐德鸿，周朝阳.并联UPS系统均流控制[J].中国电机工程学报， 2008（21）：76-84.

[6]鞠洪新.分布式微网电力系统中多逆变电源的并网控制研究[D].合肥：合肥工业大学，2006.

[7]Y ZHANG，H MA.Theoretical and experimental investigation of networked control for parallel operation of inverters[J].IEEE Transactions on Industrial Electronics， 2012，59(4)：1961-1970.

[8]于玮.UPS并联系统若干关键问题研究[D].杭州：浙江大学，2009.

[9]J Matas， M Castilla， L Vicuna.impedance loop for droopcontrolled single-phase parallel inverters using a Second-Order General-Integrator Scheme[J].IEEE Transaction on Power Electronics， 2010， 25(12)：2993-3002.

[10]梁量.分布式VSC动态虚拟阻抗优化并联策略研究[D].哈尔滨：哈尔滨工业大学，2011.

[11]J M Guerrero， J Matas， L Garc de Vicu， M Castilla.Decentralized Control for Parallel Operation of Distributed Generation Inverters Using Resistive Output Impedance[J].IEEE Trans Ind Electron，2007：994-1004.

[12]M Savaghebi，A Jalilian， J Vasquez.Secondary control scheme for voltage unbalances compensation in an islanded droop-controlled microgrid.IEEE Transactions on Smart Grid， 2011(99)：2000-2011.