混沌扩频SPWM最优参数选取方法及其在FPGA上的实时实现

朱少平，沈传文，朱立岗，徐益飞

（西安交通大学电气工程学院，陕西 西安 710049）

引言

在电力电子装置中，恒频PWM控制使得谐波能量高度集中在开关频率及其倍频附近。这些幅值较高的谐波，引起较高的电磁干扰和噪声[1]，以致影响到工业设备中其他电子装置和通信系统的正常运行[2]。引起EMI的谐波频率与开关频率有关，因而在通过扩频技术来降低EMI方面，国内外做了大量研究，其中运用较多的有周期扩频技术[3～5]、随机扩频技术[6，7]、混沌扩频技术[8]。

使用随机扩频技术，谐波能量能被扩散到连续的频谱上[9]，有较好的EMI降低效果。但由于要实现真正的随机信号十分困难并且成本很高，所以通常使用伪随机信号替代随机信号。然而伪随机信号会受到序列长度的限制，最后都会陷入周期序列影响。混沌序列由于具有内在随机性，可以用来取代伪随机信号[10]。文献[2]中采用了混沌空间矢量脉宽调制策略CFFM-SVPWM，这种策略有效降低了开关型谐波含量，并且避免了感应电动机驱动中的机械共振[11]。为提高混沌扩频PWM的抑制效果，多种改进型的混沌扩频方法被陆续提出[12-17]。但在这些通过混沌扩频降低EMI的方法中，偏置频率的大小对EMI降低效果及混沌序列的混沌程度对EMI降低效果的影响均没有论述，本文将在这两个方面做出详细分析，并将在FPGA上给出实时生成混沌SPWM的方法并验证本文所提结论。

1 混沌扩频SPWM

1.1 混沌扩频SPWM原理

扩频技术的理论基础是帕斯瓦尔 （Parseval）定理，如果信号的时域能量总和不变，那么频域的能量总和也保持不变。因而可以通过扩展开关频率，使得开关型谐波频率附近的频带宽度增加，从而降低开关型谐波的峰值。扩频技术就是用周期、随机或混沌的频率信号替换固定不变的开关频率，以达到扩展频带宽度，降低EMI的效果。混沌扩频就是将固定不变的开关频率替换为混沌的频率信号，原理图如图1所示。

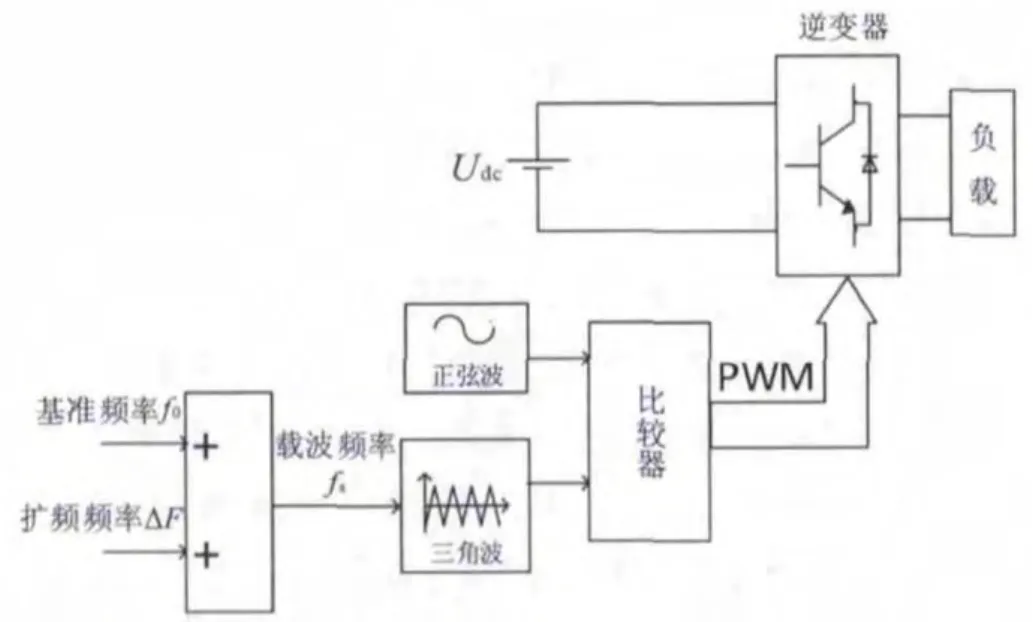
图1 混沌扩频方法原理示意图

三角载波频率fs可表示为

式中：f0为基准频率，ΔF为扩频频率。当ΔF为定值时，为传统恒频PWM调制方法；当ΔF随时间混沌变化时，为混沌扩频方法。

混沌扩频即式（1）中的ΔF选取混沌序列时的扩频方法，式中扩频频率ΔF可表示为

其中，Δf为偏置频率，表示扩频频率的变化范围，xn为混沌序列。本文选取的xn为Logistic混沌映射，其递推表达式为

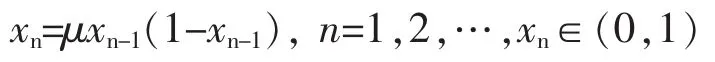
当 μ=4时，xn为混沌序列。 初始值取在（0，1）内，则迭代值在（0，1）内，其概率密度函数 p（x）为[17]

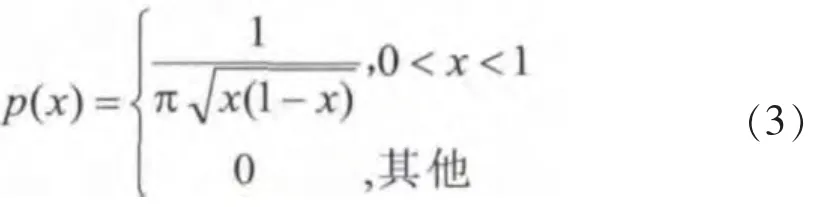
1.2 混沌扩频SPWM原理

在图1所示系统中，输出线电压的谐波电压的最大幅值出现在三角载波频率fs处，谐波电压为Uh(t)=Uhsin2πfst=Uhsin2π(f0+Δfxn)t。

由于xn为混沌变化的序列，所以谐波频谱不再是孤立的频率点，而是一段频率区间。

用Matlab进行仿真，Udc=400 V，调制度M=1，调制波 u(t)=sin(2πf1t)，f1=50 Hz；载波频率 fs=f0+Δfxn，基准频率f0=1 kHz，分别取式（1）中的扩频频率为恒值 ΔF=0.5 kHz和为混沌值 ΔF=1·xnkHz （即 Δf=1 kHz），仿真结果如图 2、3 所示。

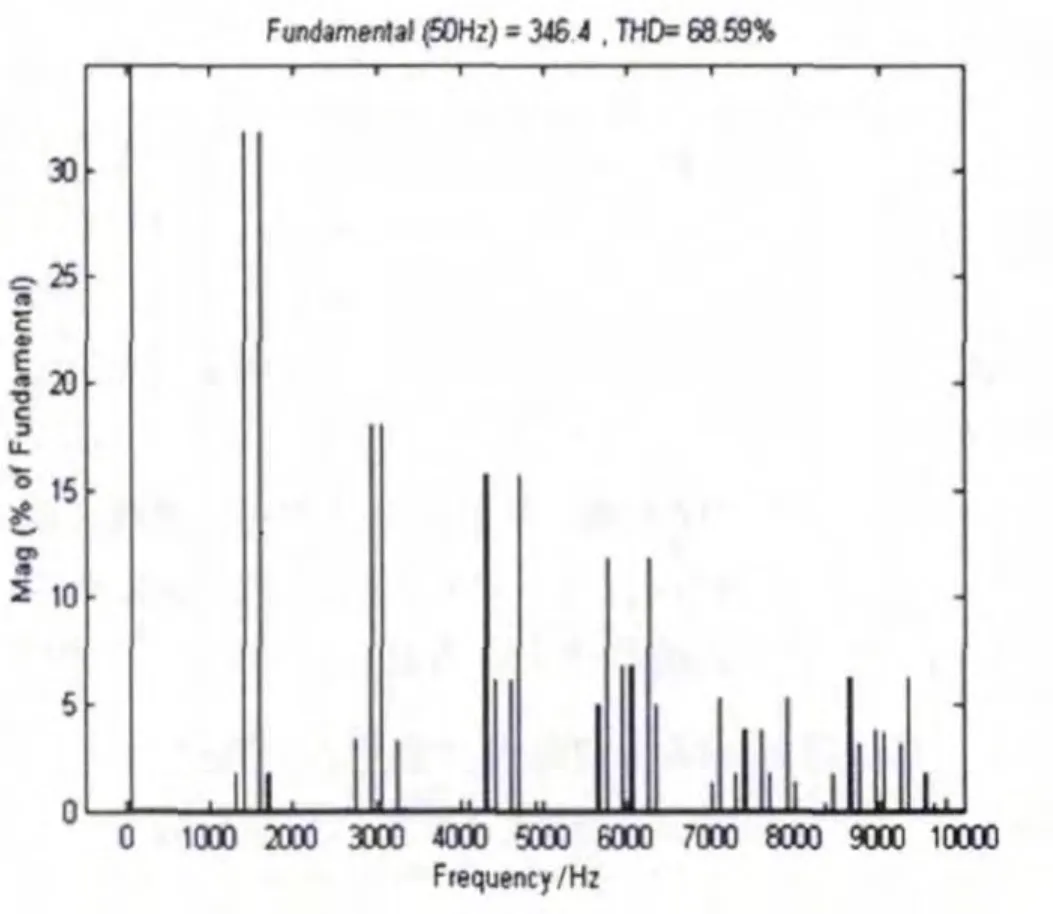
图2 传统恒频PWM输出线电压频谱

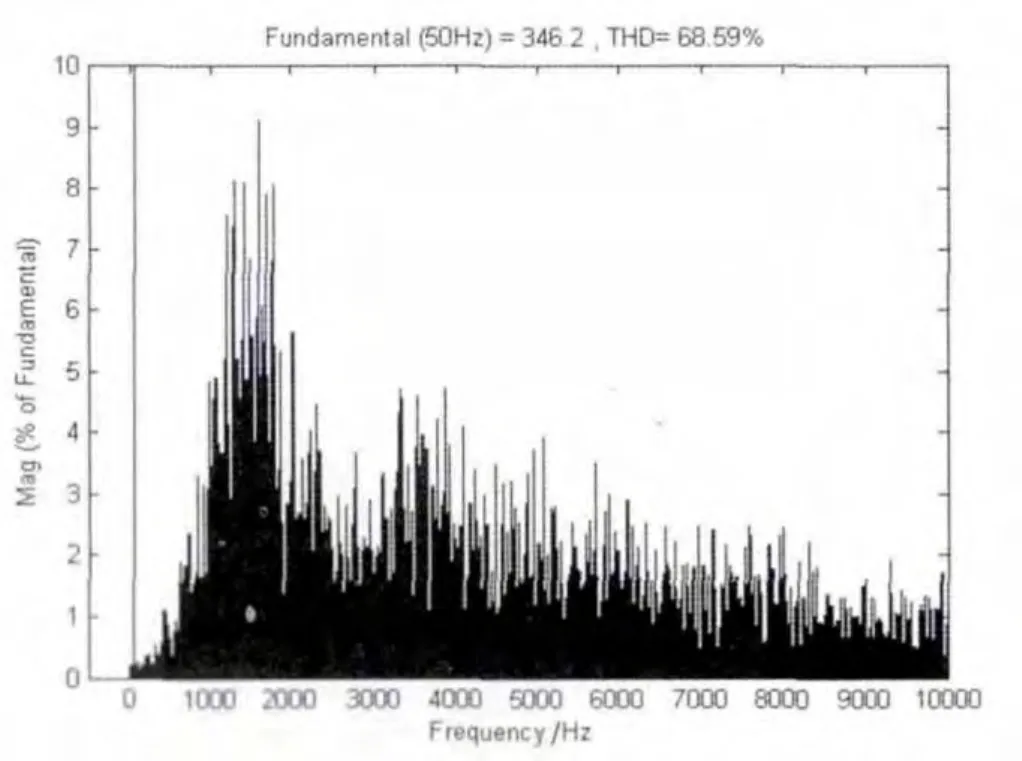
图3 混沌扩频PWM输出线电压频谱

从图2、图3的对比来看，混沌扩频后，原本为离散状态的频谱被扩散为连续分布，开关频率及其倍频附近的谐波含量明显下降，谐波峰值从30%以上降到了大约9%的水平。由此可见，混沌扩频对降低谐波含量有明显效果。而混沌扩频参数与谐波抑制效果之间的具体关系，将在下一节进行论述。

2 混沌扩频SPWM参数选择对谐波分布的影响

本章对混沌扩频SPWM中两个频率参数：基准频率f0和偏置频率Δf对谐波的含量的影响规律进行探究。

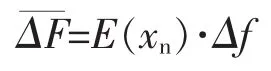
其中，E（·）为期望算子，xn为混沌序列，本文选取为 Logistic 序列，E（xn）=0.5，因而记此时的为半偏置频率fh，即fh=0.5Δf。则平均开关频率因而基准频率f0与半偏置频率fh的和即为平均开关频率。

2.1 基准频率和偏置频率与谐波峰值削弱效果的关系

如前文提到的，扩频SPWM调制下谐波总含量保持不变，因而扩频SPWM调制可以看作是谐波能量的重新分配，即将含量较高的低次谐波能量分散到连续的频谱上，从而削弱谐波峰值。因此本文以对谐波峰值的削弱效果来研究扩频方法的谐波抑制效果。

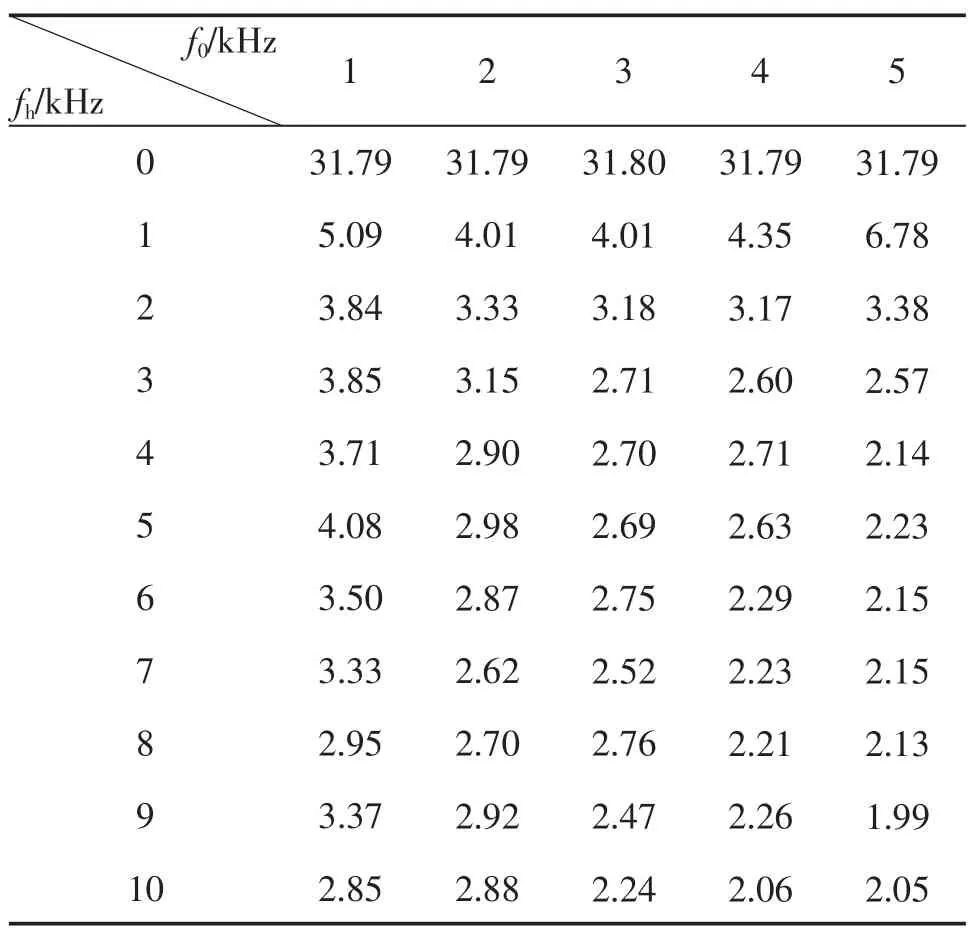
表1 基准频率f0和半偏置频率fh不同组合下谐波峰值占基波幅值的百分含量（%）

用Matlab进行仿真，Udc=400 V，调制度M=1，调制波 u(t)=sin(2πf1t)，f1=50 Hz；三角载波基准频率 f0分别取1～5 kHz， 半偏置频率 fh分别取 0～10 kHz，基准频率f0和半偏置频率fh的不同组合对应的谐波峰值占基波幅值的百分含量如表1所示。

观察表1数据，可以得出如下规律：

(1)不扩频时，谐波峰值不随基准频率f0的增加而改变。混沌扩频后，谐波峰值与不扩频相比，有明显下降。

(2)当存在混沌扩频且半偏置频率fh一定时，若基准频率f0小于半偏置频率fh的2倍，则谐波峰值随基准频率f0的增加而降低；反之，若基准频率f0大于半偏置频率fh的2倍，则波峰值随基准频率f0的增加而增加。

(3)当基准频率f0在半偏置频率fh的2倍以内时，谐波峰值随平均开关频率fs的增加而降低。

分析以上规律，可以发现，若要在不增加平均开关频率fs的前提下，更多地降低谐波峰值，半偏置频率fh至少需要设置为基准频率f0的50%。下面分析当平均开关频率一定时，要使谐波峰值降到最低，半偏置频率fh与基准频率f0之间应满足的比例关系。

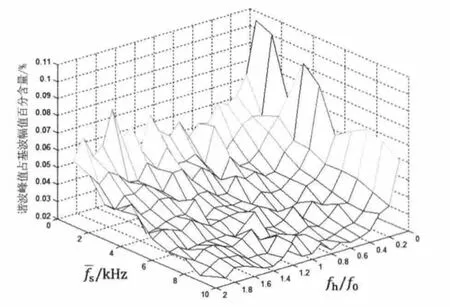
图4 平均开关频率fs、半偏置频率fh与基准频率f0的比值、谐波峰值占基波幅值的百分含量的三维图像

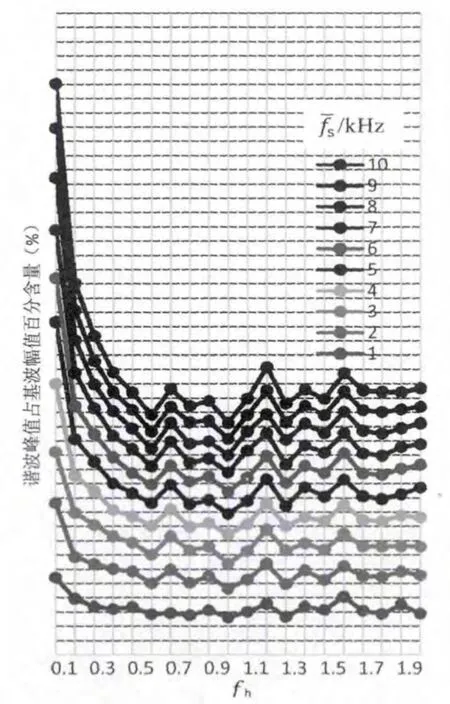
图5 在不同的平均开关频率下，谐波峰值占基波幅值的百分含量随半偏置频率fh与基准频率f0比值的变化趋势图线

从图4、5可看出，若平均开关频率为定值，大体上时，半偏置频率fh与基准频率f0比值在1附近时，谐波峰值最低。

这个结论提供了混沌扩频SPWM技术在实际应用中选择开关频率参数的一种方法。即当开关器件的平均开关频率选定之后，应将基准频率和半偏置频率设置为相等，此时可以让谐波峰值最低。

2.2 基准频率和偏置频率对谐波频谱分布均匀程度的影响

混沌扩频SPWM可以使原本离散的输出线电压频谱分布变为均匀连续，基准频率和偏置频率不同，其分布的均匀程度也不同。谐波分布均匀程度可以用谐波幅值标准差表征，谐波幅值标准差计算公式如下

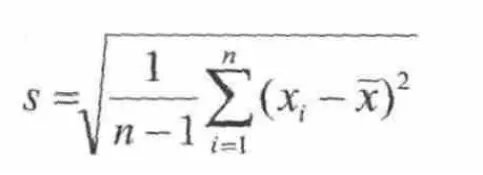
其中，n为频谱计算时所取频点的个数，xi为第i个频点对应的谐波幅值，为n个频点对应谐波幅值的平均值。

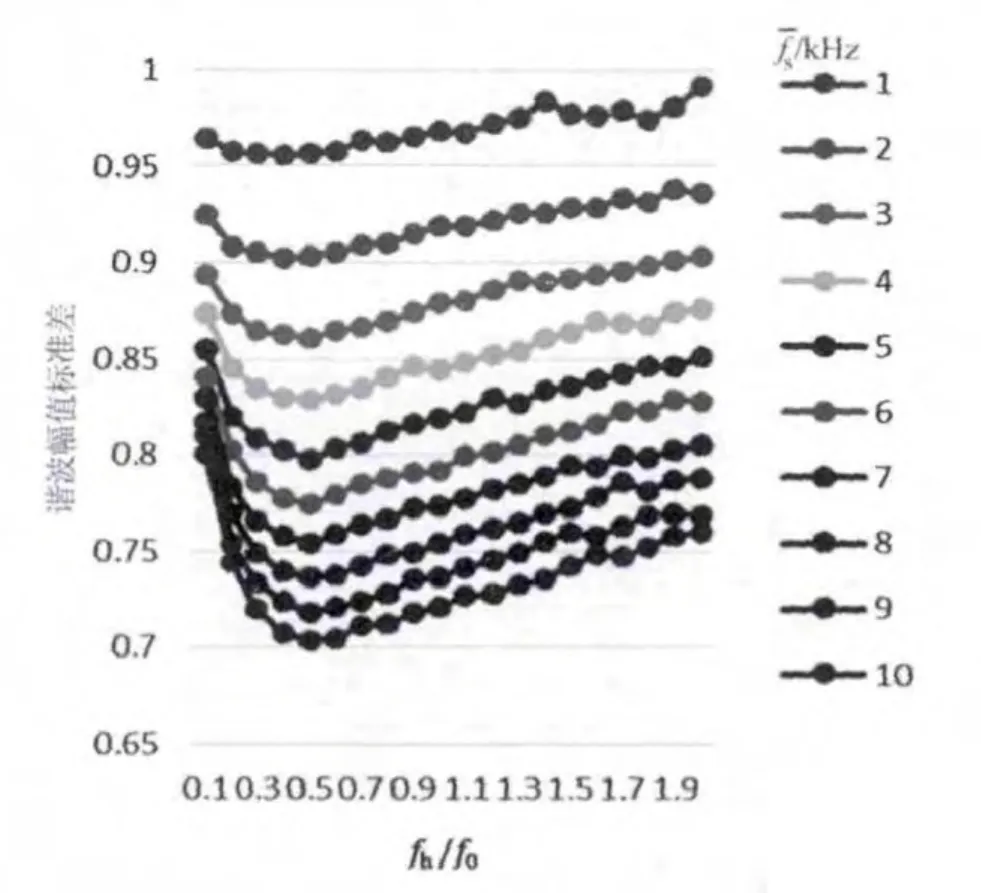
图6 谐波幅值标准差随半偏置频率fh与基准频率f0的比值的变化曲线

图6 所示的仿真结果一致地表现出一个结果，即当半偏置频率fh为基准频率f0的0.5倍时，谐波幅值标准差最小，即此时的谐波分布最均匀。且当半偏置频率fh大于基准频率f0的0.5倍时，谐波分布均匀程度随着fh的增大而降低。

3 混沌扩频PWM在FPGA上的实时实现

3.1 实现原理

混沌扩频PWM是在恒定的开关频率上增加一个混沌变化的开关频率。用FPGA实时实现，开关频率就对应的是三角载波的频率，即给定的三角波频率是一个恒定频率加一个混沌变化的频率。

混沌频率三角波的实现流程图如图7所示。其中计算三角波输出变化值Sdelta=f·2DT中的T为FPGA的指令周期。

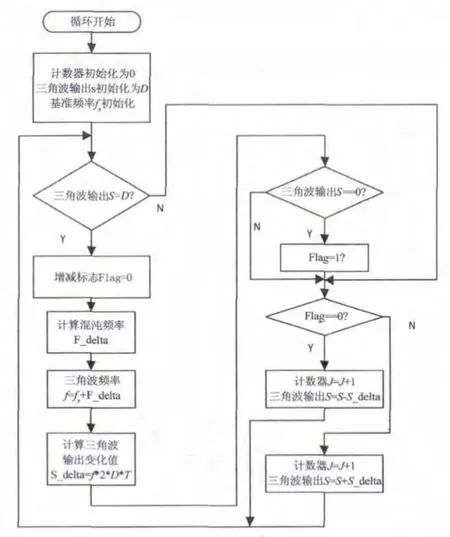
图7 混沌频率三角波的实现流程图

3.2 FPGA硬件仿真结果

在FPGA中，可以通过实时计算的方法获得Logistic混沌序列，xn=4xn-1(1-xn-1)的FPGA的仿真波形如图8所示。

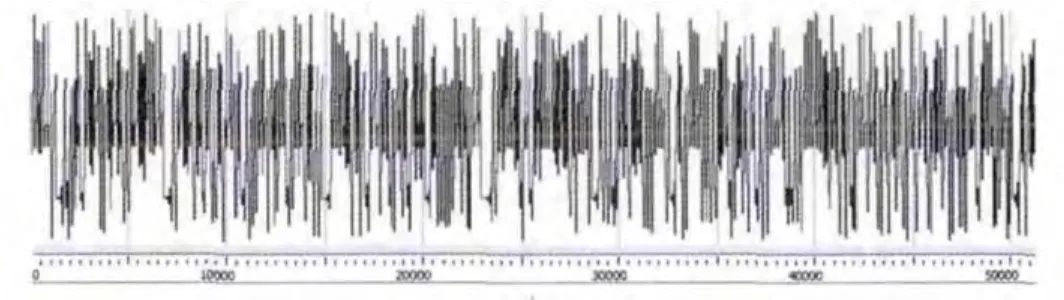
图8 FPGA硬件仿真Logistic混沌序列波形

按照图7流程图所示原理，可以实现频率混沌变化的三角载波。

混沌三角波扩频示意图如图9所示，在每个三角波周期开始时更新一次频率，从而达到三角波频率混沌化的目的。

在FPGA的专用仿真软件Modelsim平台下进行实验验证，取正弦波频率为50 Hz，三角波平均频率为2.5 kHz。对应的基准频率为1.25 kHz，半偏置频率为1.25 kHz，其波形如图10所示。

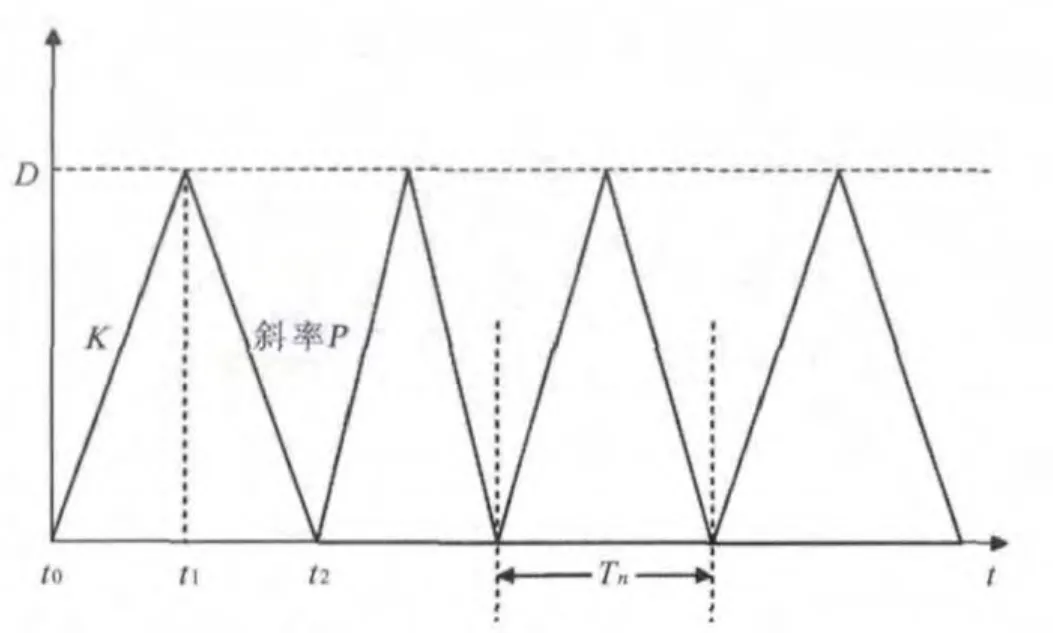
图9 混沌三角载波扩频原理示意图

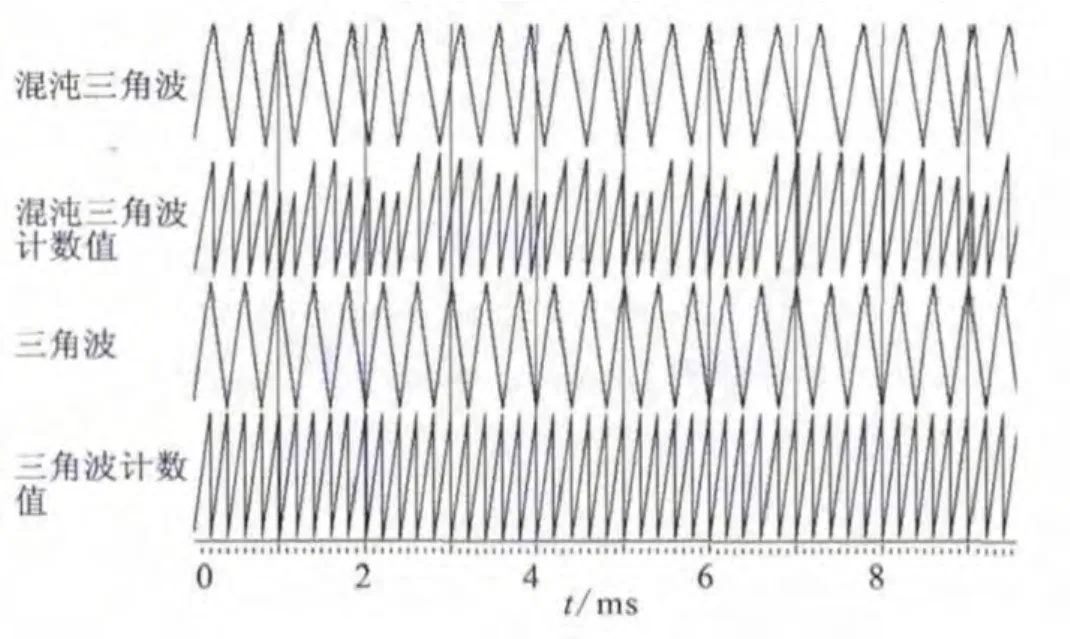
图10 混沌三角波

图10 中所示第一、二行分别为混沌三角波及其计数值。第三、第四行分别为未经混沌扩频的三角波及其计数值。此时正弦波频率为50 Hz，此时载波比为50。可见，每一个三角波周期对应的频率都各不相同。

利用生成的混沌三角波进行混沌SPWM波调制，波形如图11所示，第一行为基波波形，第二、三行分别为混沌三角波及其PWM波形，第四、五行为普通三角波及其PWM波形。

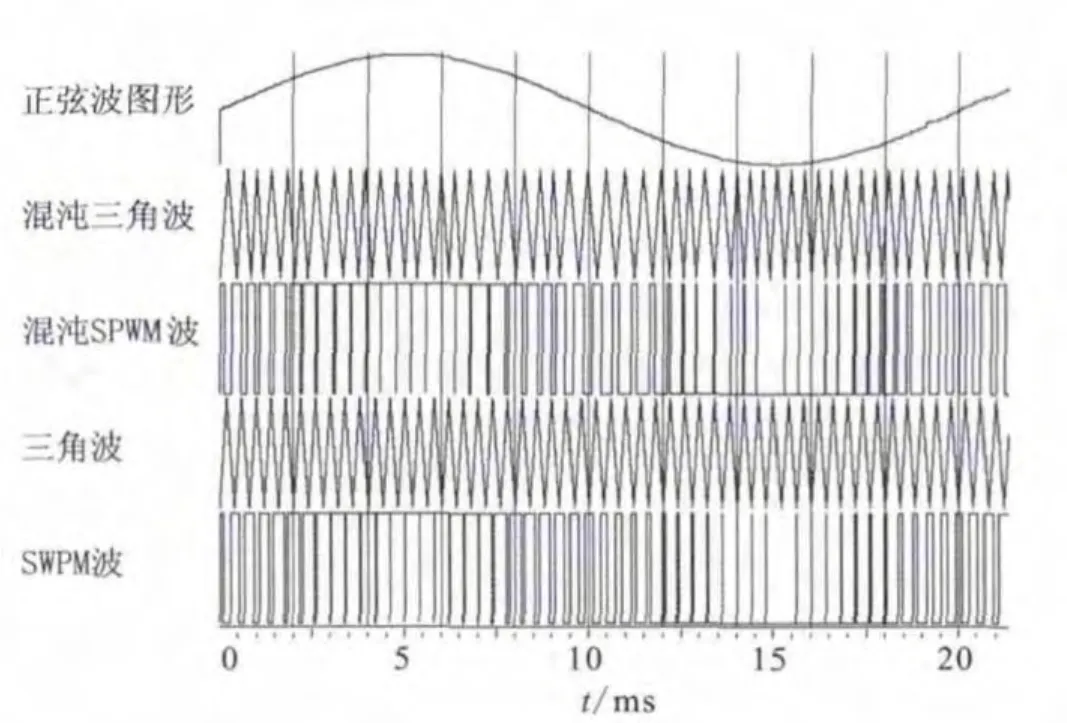
图11 混沌SPWM波调制波形

用上述方法，在保持平均开关频率为2.5 kHz的情况下，对不同半偏置频率fh与基准频率f0的组合进行FPGA仿真，用Matlab软件对仿真产生的SPWM波进行频谱分析，得到如图12所示频谱分析结果，其中从左到右，fh与f0的比值分别为4，1.5，1，0.67，0.25。

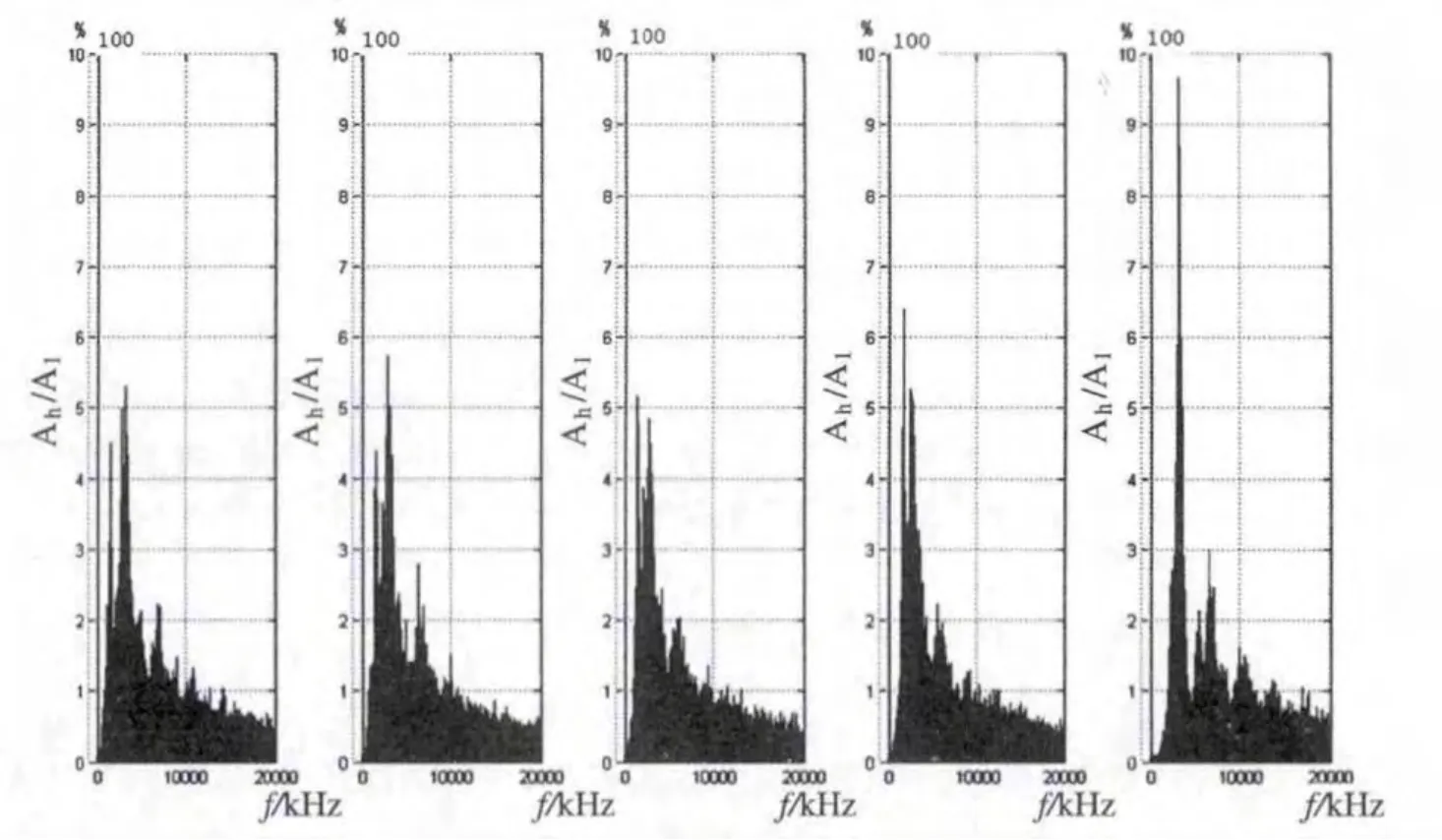
图12 混沌SPWM波频谱分析

从图12的结果可以看出，在平均开关频率一定时，当半偏置频率fh与基准频率f0相等时，谐波峰值含量最低，对谐波的抑制效果最好，通过实验证实了前文所述结论。

4 结论

本文以基于Logistic映射的混沌扩频SPWM技术应用方法为例，通过定量分析基准频率和偏置频率对谐波分布的影响效果，给出了工程实验结论：在平均开关频率为定值的情况下，当半偏置频率为基准频率1倍时，谐波峰值含量最低；当半偏置频率为基准频率0.5倍时，谐波分布最均匀。从而提出了一种混沌扩频中基准频率和偏置频率的最优选取方法；给出在FPGA上实时生成混沌SPWM的方法，并通过FPGA仿真验证了前述结论。

[1]刘洪臣,庄严,孙立山,刘雷.基于混沌扩频的双级矩阵变换器调制策略的研究[J].电源学报,2012（6）：9-13.

[2]王政，邹国棠，程明.基于混沌SVPWM的矢量控制感应电动机驱动[J].电工技术学报，2009，24(11)：34-40.

[3]BALCELLS J,SANTOLARIA A,ORLANDI A.EMI reduction in switched power converters using frequency modulation techniques[J].IEEE Transactions on Electromagnetic Compatibility,2005,47(3)：569-576.

[4]ATSUMI Y,FUJII K,SUGIURA A.An analytical method for Determining the optimal modulating wave form for dithered clock generation.IEEE Transactions on Electromagnetic Compatibility,2005,47(3),577-584.

[5]罗萍,李肇基,熊富贵,陈光.PSM开关变换器的平均模型与特性分析[J].电工技术学报,2005,20(3)：19-23.

[6]C B Jacobina,A M N Lima,et al.Current Control for Induction Motor Drive Using Random PWM.IEEE Trans.On Industrial Electronics,1998,45(5)：704-712.

[7]王斌,李兴源,K EI Khamlichi Drissi.双随机调制技术及其功率谱密度特性分析[J].中国电机工程学报,2004,24(4)：97-101.

[8]高金峰,黄明明,赵坤.应用混沌控制降低Boost型变换器EMI水平研究[J].电力电子技术,2004,38(3)：82-85.

[9]周伟英,丘水生,朱辉.不同扩频信号对开关功率变换器EMI抑制效果的比较[J].电气应用,2008,27(2)：83-86.

[10]杨蕾,单潮龙.双混沌SVPWM技术及其功率谱密度特性分析[J].华东电力,2013,41(3)：0579-0583.

[11]Lo W C,Chan C C,Zhu Z Q,et al.Acoustic noise radiated by PWM-controlled induction machine drives[J].IEEE Transactions on Industrial Electronics,2000,47(4)：880-889.

[12]Hong li,Fei Lin,Xiajie,Trillion Q Zheng,et al.The application of chaotic PWM control for EMI Suppression.The International Journal for Computation and Mathematics in Electrical and Electronic Engineering,2013,32(3)：750-762.

[13]范九伦,张雪锋.分段Logistic混沌映射及其性能分析[J].电子学报,2009,37(4)：720-725.

[14]ZHOU Liang-qiang,CHEN Fang-qi,CHEN Yu-shu.Chaotic behavior on reduction of perturbed Kdv equation in form of parametric excitation[J].Trans of Nanjing University of Aeronautics,2007,24(4)：283-287.

[15]周志刚,徐江峰,李苏贵.多级混沌映射变参数伪随机序列产生方法研究[J].数学的实践与认识,2009,39(3)：166-171.

[16]李孟婷,赵泽茂.一种新的混沌伪随机序列生成方法[J].计算机应用研究,2011,28(1)：341-344.

[17]陈式刚.映像与混沌[M].第1版.北京：国防工业出版社,1992.

[18]R Lynn Kirlin,Andraej M Trzynadlowski.Power Spectra of a PWM Inverter with Randomized Pulse Position[J].IEEE Transactions on Power Electronics,1994,9(5)：463-472.

[19]李冠林,陈希有,刘凤春.混沌PWM逆变器输出电压功率谱密度分析[J].中国电机工程学报,2006,26(20)：79-83.