空间非编码标记特征点中心定位方法与比较

（北京空间飞行器总体设计部，北京 100094）

1 引言

目前，面向空间应用的可见光视觉测量系统已成为许多深空探测器、货运飞船和侦察卫星［1-2］等航天器的重要载荷之一，它主要由布置在目标体（或目标飞行器）上的空间视觉标记及装载在航天器上的空间相机和数字图像处理软件等3部分组成。其基本原理［3］在于：采用单台或多台载荷相机实时观测、采集已知形状尺寸特征的空间标记图像，利用数字图像处理准确定位标记特征点中心坐标值，并构建视觉标记特征点及其在2D 像面中所提取的点中心坐标值之间一一对应的函数映射关系，最终可解算视觉标记与空间相机之间的相对位姿关系。

空间视觉标记以其自身的已知几何特征信息，为目标位姿解算提供了可靠的依据和基准。它主要有两个关键环节：标记图案设计与特征点中心定位。标记图案设计主要包括非编码图案和编码图案两种［4］：前者采用组合同类规则几何形状的图案设计；后者则依据不同的编码策略，生成多种具有旋转、缩放唯一性的复杂图案。相比于编码图案，非编码图案具有设计简单、安装方便、环境适应性强、特征点中心易于提取等显著优势。目前，“国际空间站”主要采用了非编码图案设计，空间站表面粘贴了若干圆型点状标记簇［5］，各圆型标记点直径约1m，粘贴或安装厚度约1mm，圆直径在图像中占据10～15个像素，且上述标记点均采用一种包含双层结构的特殊材料：上层白色实心圆采用了二氧化硅，下层黑色圆环采用了镍铝合金，以显著增强标记的黑白对比度。此外，应用于航天飞机的“加拿大臂”（Canadarm）也采用了非编码设计空间标记［6］，呈共面分布的2行6列矩形方格图案固定安装在臂杆上，每个方格尺寸约50mm×50mm，在图像中占据不少于100个像素。显然，非编码设计并不唯一，具有多种图案表现形式。不同的非编码图案设计将直接制约着特征点中心定位的准确性和难易程度，而定位结果又作为已知系数参量参与目标空间位姿的实际解算，这势必会影响可见光系统最终的测量精度。

为此，本文归纳总结了空间标记非编码设计原则，着重介绍了棋盘格型、栅格型、圆型等3种典型的非编码图案标记设计，详细分析了各种标记特征点中心定位方法和计算过程，并开展试验对上述标记图案及其点中心定位算法进行对比和分析。

2 空间标记非编码设计原则

面向可见光空间测量应用的空间标记非编码设计［4，7］原则主要包括以下几方面：

（1）图案设计必须为具有同类规则的几何形状组合，例如：圆型阵列、矩形阵列等；

（2）图案设计切忌过于复杂，以确保特征点中心易于快速、准确提取；

（3）图案设计应以适宜的尺寸成像，且保持尽可能高的亮暗对比度；

（4）图案设计易于粘贴、安装、布置在航天器表面。

此外，空间标记数目与分布应结合空间相机的视场角以及空间目标外形尺寸等予以充分考虑，原则上空间标记的个数应为不小于4的任意整数；空间标记可随意分布在目标表面，确保各标记点均能在相机中清晰成像，且不与其他设备发生干涉、遮挡等现象。

空间标记非编码设计并不拘泥于某一种或几种特定的图案，可以具有多种图案表现形式，只要满足上述设计原则即可。目前常用的空间非编码图案标记［4-6］主要包括棋盘格型图案标记、栅格型图案标记和圆型图案标记等3种典型图案设计，分别如图1～3所示，均满足上述非编码设计要求，其图案设计简单、且保证很高的黑白对比度，更为重要的是，能够确保特征点中心的自动识别与精确定位。

图1 棋盘格型标记示意图Fig.1 Checkerboard target

图2 栅格型标记示意图Fig.2 Grid target

图3 圆型标记示意图Fig.3 Target with a cycle matrix

3 非编码标记特征点中心定位算法

现针对棋盘格型、栅格型和圆型等3种视觉标记图案设计，详细讨论其相应的2D 成像特征点中心定位算法。

3.1 棋盘格型标记

如图1所示，黑白棋盘格是一种十分常见的空间标记图案，其中每个角点即为待定位的图像特征点。目前有许多角点的提取算法，这些算法总体上可分为两种：第一种是先提取图像边缘，以链码形式表示，再寻找最大曲率处作为角点；第二种是直接计算图像灰度分布的曲率，将曲率最大的点视为角点。文献［8］指出，第二种算法比第一种算法更具有明显优势，其算法简捷、运算效率高，尤以Harris角点探测器［9-10］为典型代表。Harris角点探测器主要利用灰度自相关函数表示相邻像素间的灰度变化，其基本思想用数学形式表示如下：

先定义灰度自相关函数为

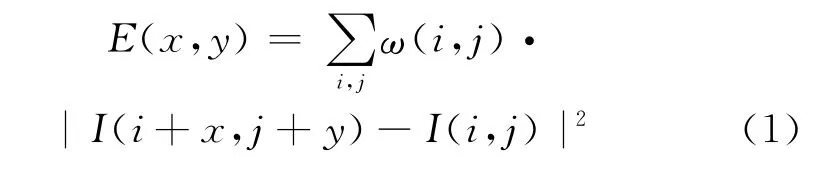
式中：ω（i，j）为像平面上一个尺寸大小为i×j的平滑高斯窗函数；Ⅰ（i，j）表示像面坐标（i，j）处所对应的灰度值。式（1）中的灰度自相关函数E（x，y）反映了在像面坐标（i，j）处存在一个（x，y）平面偏移所得到的灰度平均变化量。根据角点的性质可知，像平面在角点处的图像窗口偏移会导致上述自相关函数发生剧烈变化。

在像面坐标（i，j）处，灰度自相关函数E（x，y）可以近似为一阶Taylor多项式展开得到

整理可得

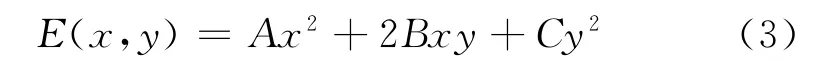
现将式（3）改写为以下形式：

式中的系数矩阵M定义为灰度自相关函数E（x，y）的Hessian矩阵，即

式中：｜M｜表示矩阵的行列式；tr（M）则为矩阵的迹。根据上述定义可知，矩阵M的特征值能够表示灰度自相关函数的极值变化情况。倘若M的两个特征值均较小，则说明像平面窗口区域亮度变化不明显；倘若M的两个特征值中其中一个较大，而另一个较小，则表明像面窗口区域处于图像边缘区域；倘若上述两个特征值均较大时，则可认定像面窗口区域此时位于角点处。

Harris角点探测器可用数学公式表示如下：

在实际操作过程中，可以设定某一个阈值RT，若R（x，y）超过某一阈值，则可认为该点为角点。实践证明，系数k通常可取0.04～0.06之间，能够获得理想的结果。在Harris角点探测器的实际计算过程中，需要涉及到卷积运算，计算量相对较大，且其角点探测精度仅为像素级。为了进一步实现角点的亚像素精度级提取，需要将角点所在邻域的像素灰度值进行高斯曲面拟合，高斯曲面的顶点即为角点中心的精确位置。具体计算如下：

假设待拟合的高斯曲面函数为

式中：（x0，y0）即为角点中心2D 坐标值。上述二维高斯曲面函数具有可分离特性，即

这样就可以将二维的高斯曲面拟合转换为两个一维的高斯曲线拟合来完成。现以x的一维高斯曲线拟合得

式中：a0＝对x方向上的点进行拟合，用最小二乘法可以求得二次多项式的系数a0，a1，a2，即可得出即为角点中心的x轴坐标分量，同理可计算出角点中心的y轴坐标分量。

3.2 栅格型标记

图2表示了一种栅格型标记图案，其中每个栅格点即为待提取的空间标记2D 成像特征点。国内外许多学者针对栅格型标记特征点中心的定位问题，提出了多种不同的定位算法，主要可分为两大类［8，11］：一类是利用图像灰度分布的梯度信息来识别栅格点，此类方法通常定位精度难以达到亚像素级，而且运算量较大，极容易误判和丢失栅格点；另一类是根据栅格图案设计的直线几何特征，先提取出栅格边缘点以拟合成直线，随后求直线的交点即为栅格点，此类方法运算量比较小，定位精度通常在亚像素级别。下面将着重介绍第二类算法的基本原理。

在数字图像处理领域中，Hough变换［12］常用于检测直线。如图4所示，现假设像平面坐标系o-uv，像面上任一条直线l，位于该直线上的任一点P的像面坐标值为（u0，v0），像面坐标系原点o至直线l的欧氏距离可设为d，将点P与坐标原点o连接成为直线段，该线段长度为ρ，则与u轴之间的夹角为α，且直线l与u轴之间的夹角为β。根据图4中的平面几何关系可得

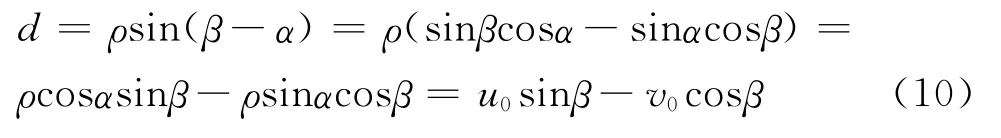
图4 Hough变换数学模型示意图Fig.4 Mathematical model of Hough transformation

现定义（d，β）为描述像平面中任一条直线的表示参数。由式（10）可以看出，在o-uv中任意的一个点都对应参数空间中的一条曲线。只要是同一个直线上的点，它们对应的曲线就会有一个交点，该交点对应的d和β即为该直线的参数。

以Hough变换为基础检测一幅图像中的直线，将参数空间中所有交点对应的曲线个数记录下来，个数越多说明构成该直线的点就越多。只要设置一个阈值，大于该阈值的参数就认为是图像中的直线。在算法中，为了提高Hough 变换检测直线的分辨率，尽量减小d和β的取值间隔。

然而传统的Hough变换定位精度并不理想，在许多场合中应用Hough变换检测直线都存在一个共性问题，即如果阈值选取不合适，同一组直线边缘点将有可能检测出多于一条直线参数的结果。图5中的黑色区域表示栅格点所在直线的边缘区域，而蓝色细直线则反映了传统Hough变换直线检测结果。从图5中可以清楚地看到，Hough变换检测到的直线不仅定位不够准确，而且会出现多条直线的情况。

图5 Hough变换直线检测Fig.5 Line detection by Hough transformation

针对上述问题，本文设计了一种改进的Hough变换特征点定位算法：首先，手动设置栅格点的个数及子区域尺寸阈值，并利用Canny算子检测图像边缘，根据子区域阈值大小，将包含栅格点的区域分割成若干子区域，并且每个区域中均保证只包含一个栅格点；其次，利用Hough变换完成每个子区域的直线检测，确定对应的直线参数；再次，任意选取两条存在一定角度的直线，根据直线参数判断各直线方向，分别沿每条直线的法线方向上遍历搜索阈值边缘点；随后，对沿该直线方向搜索到的全部边缘点利用最小二乘直线拟合，即可获得相应直线方程；最后，联立两个直线方程即可计算栅格点的像面坐标位置。

上述方法是在Hough 变换直线检测的基础上，引入遍历搜索阈值边缘点和最小二乘直线拟合，从而准确定位栅格点中心坐标。因此，此方法的优势表现为：它不仅继承了传统Hough变换算法计算量小、计算速度快等优点，还能妥善解决因Hough变换阈值选取不当而引起的边缘定位误差问题，并且有效提高了原有Hough变换的特征点定位精度。

3.3 圆型标记

图3是目前应用最为广泛的一种空间标记图案设计，其自身优势是：图案中的每个独立圆型标记均呈中心对称分布，其在相机成像面中始终呈现各向同性特征，有效规避了由于其他外界干扰所导致的标记变形问题而影响特征点中心的自动识别与提取。如图3所示，每个圆型区域的中心即为待求取的图像特征点。鉴于这种靶标图案十分易于识别且定位精度较高，受到众多学者的青睐，相继提出了许多圆型点中心定位算法，例如：质心法、灰度平方加权质心法、高斯加权质心法和椭圆拟合法等。文献［13-14］指出，质心法和椭圆拟合法相对简单，对于规则圆型图像具有较高的定位精度，但不适用于不规则的圆型图像；高斯加权质心法能够有效抑制高斯噪声产生的影响；灰度平方加权质心法采用灰度值的平方作为权值系数，突出了离中心较近且灰度值较大的像点对中心位置的影响。相比之下，灰度平方加权质心法的算法稳定、整体性能最高、可适用于多种噪声环境和畸变图像。

现将灰度平方加权质心法的计算过程表示如下：假设在圆型标记图案中的其中一个黑色圆型区域所含像素个数为M×N，Ⅰ（x，y）表示像面坐标值（x，y）处所对应的灰度值，则需要提取的该圆型区域中心位置可以设为（x0，y0）。根据圆型区域的像素灰度分布特性，利用灰度的平方作为权重因子，可以按照以下公式计算该圆区域的中心位置。

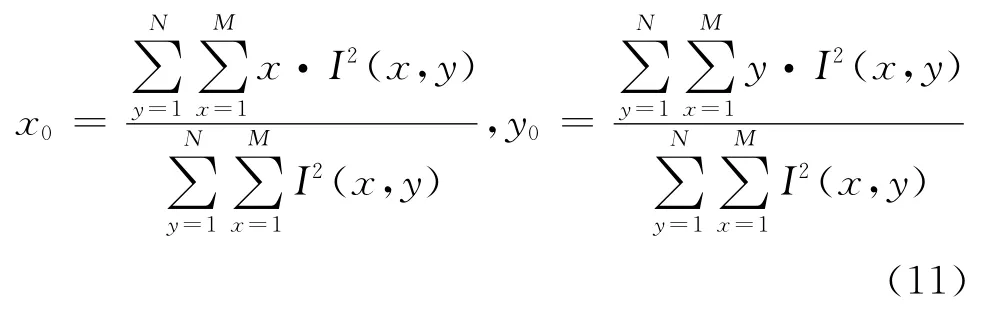
由式（11）可知，圆型区域中心位置同时受像素坐标值及其对应的灰度值共同影响，即离中心点越近且灰度值越大的像素点对中心位置的计算影响显著。此方法具有很好的鲁棒性和自适应能力，它既能够适用于圆型区域像素灰度分布近似于高斯分布，且圆型区域相对规则，包含足够多的像素情况；也特别适合所占像素相对较少，呈现光斑形状不规则的圆型区域。

4 试验结果与分析

鉴于上述分析可知，前面介绍的3种视觉标记所对应的特征点中心定位算法均可视为同类算法的优选方案，下面将着重针对棋盘格型标记、栅格型标记和圆型标记等非编码视觉标记设计及其点中心定位算法开展对比试验。

首先，分别设计了3 种标记图案分别为图6（a）、图7（a）、图8（a），它们均呈平面分布，每种图案都包含了8 行10 列共计80 个待检测的有效特征点，且所有特征点都尽可能均匀分布在目标的平面上，便于被相机视场覆盖，其中，棋盘格型和栅格型图案中的每个小格尺寸均为30mm×30mm，圆型图案中的每个圆点直径为10 mm。每种图案仅采用黑白两种颜色，以保证高对比度。

其次，利用同一台工业级Nikon D2H 量测相机分别采集了上述3种标记图案的图像信息，见图6（a）、图7（a）、图8（a），要求标记图案尽可能充满整个视场，以防止图像中掺杂任何干扰信息。其中，相机分辨率最高可达4288×2848pixels，像元尺寸为6μm。随后，分别将上述3幅图像输入计算机保存。

再次，在Matlab软件平台中，针对不同标记图案，分别调用前面介绍的最优算法的软件程序，完成图像中每一个特征点的自动识别和点中心精确定位，见图6（b）、图7（b）、图8（b），最终可分别获得3组具有亚像素精度的标记特征点中心的2D 图像坐标值序列，为方便起见，现将所有点中心位置均标识在原始图像中，具体结果如图6（c）、图7（c）、图8（c）所示。

图6 棋盘格型标记图像点中心定位结果Fig.6 Experiment of center positioning and extraction algorithms of 2Dimage feature points for spatial target with a checkerboard pattern

图7 栅格型标记图像点中心定位结果Fig.7 Experiment of center positioning and extraction algorithms of 2Dimage feature points for spatial target with a grid pattern

图8 圆型标记图像点中心定位结果Fig.8 Experiment of center positioning and extraction algorithms of 2Dimage feature points for spatial target with a cycle matrix pattern

最后，利用仿真分析验证上述点中心定位算法的性能。现将前面采集到的棋盘格型标记、栅格型标记和圆型标记的图像视为原始图像，分别在每幅图像中加入一组均值为零、均方根分别为｛σn＝0，0.02，0.04，0.06，0.08，0.1｝的高斯白噪声，反复调用相应的点中心定位算法的软件程序进行特征点自动识别与点中心定位操作。图9～图11分别给出了3种标记图案特征点中心定位算法在不同噪声水平下的性能，包括成功定位特征点个数、计算时间及点中心定位精度。

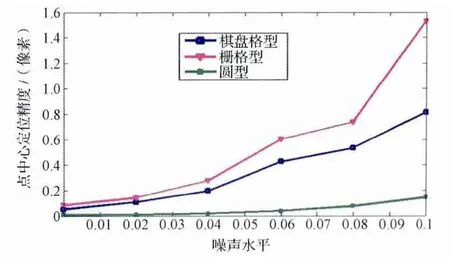
图9 三种标记图案特征点中心定位算法点中心定位精度比较Fig.9 Comparison of accuracy of different center positioning algorithms responding to three patterns

图10 三种标记图案特征点中心定位算法计算时间比较Fig.10 Comparison of calculating time of different center positioning algorithms responding to three patterns

图11 三种标记图案特征点中心定位算法成功定位特征点个数比较Fig.11 Comparison on number of image feature points responding to three patterns by different center positioning algorithms

从图9中可以看出，在定位精度方面，圆型标记特征点中心定位精度最高，棋盘格型标记点中心定位算法次之，栅格型标记成像点中心定位精度相对较低。根据图10可知，在运算效率方面，圆型标记点中心定位算法的运算时间最短，其计算效率高于棋盘格型标记点中心定位算法，而栅格型标记点中心定位计算时间相对较长。如图11所示，在抗噪声方面，圆型标记点中心定位算法十分稳定，其定位精度受噪声影响最小，始终能够将所有特征点中心准确定位，说明该方法具有较强的噪声抑制能力；尽管棋盘格型标记点中心定位算法定位精度，随着噪声的增大呈现出逐步上升趋势，但始终未偏离1个像素；相比之下，栅格型标记点中心定位算法的抗噪声能力相对较弱。需要指出的是，上述点中心定位算法的性能差异并不仅仅体现为算法自身，它与标记图案设计密切相关，只有将二者有机结合在一起，进行对比与分析，才能够正确客观地评价标记整体方案的优劣。

因此，圆型标记整体方案（含图案设计和中心定位算法）明显优于其他两种标记方案，其特征点中心定位精度、计算效率、稳定性和抗噪声性能更有利于保证可见光视觉测量的高精度，应作为空间视觉标记的首选方案。

5 结束语

空间视觉标记在面向空间应用的可见光测量系统中占有举足轻重的地位，可用于空间相机标定、合作目标3D 轮廓特征重构和空间位置姿态精确估计等。空间标记的关键技术环节是：标记图案设计及其特征点中心定位算法，不同的图案设计将直接制约着特征点中心定位算法的难易程度和准确性，从而会影响可见光系统最终的测量精度。本文在系统总结非编码标记设计原则，深入剖析棋盘格型、栅格型、圆型等标记特征点中心定位算法的数学内涵的基础上，开展了对比试验，结果表明：圆型标记凭借其自身的各向同性优势，以及特征点中心定位算法具有速度快、精度高、抗噪性强等优点，明显优于其他两种图案设计。因此，圆型标记应作为空间标记的首选方案，这一结论与“国际空间站”的成功经验相吻合。

（References）

［1］曹喜滨，张世杰.航天器交会对接位姿视觉测量迭代算法［J］.哈尔滨工业大学学报，2005，37（8）：691-694 Cao Xibin，Zhang Shijie.An iterative method for visionbased relative pose parameters of RVD spacecrafts［J］.Journal of Harbin Institute of Technology，2005，37（8）：691-694（in Chinese）

［2］徐鹏，黄长宁，王涌天，等.航天光学遥感器目标与背景仿真系统研究［J］.系统仿真学报，2003，15（12）：1763-1765 XU Peng，HUANG Chang-ning，WANG Yong-tian，et al.Studying aphysical simulation system for characteristics in targets and backgrounds of the remote sensor on spaceborne［J］.Journal of system simulation，2003，15（12）：1763-1765（in Chinese）

［3］陈世平.空间相机设计与试验［M］.北京：中国宇航出版社，2009 Chen Shiping.Design and experiment of space camera［M］.Beijing：China Astronautics Press，2009（in Chinese）

［4］冯文灏.近景摄影测量［M］.武汉：武汉大学出版社，2002 Feng wenhao.Close-range photogrammetry［M］.Wuhan：Wuhan University Press，2002（in Chinese）

［5］National Research Council Canad.Space vision system helps astronauts see in space［EB／OL］.［2008-02-28］.http：／／www.nrc-cnrc.gc.ca／eng／education／innovations／discoveries／svs.html

［6］Canadian Space Agency.The space vision system［EB／OL］.［2011-11-07］.http：／／www.asc-csa.gc.ca／eng／canadarm／missions／vision.asp

［7］张广军.视觉测量［M］.北京：科学出版社，2008 Zhang Guangjun.Vision measurement［M］.Beijing：Science Press，2008（in Chinese）

［8］Liu JunJie，A.Jakas.A comparative study of different corner detection methods ［C］／／IEEE International Symposium on Computational Intelligence in Robotics and Automation.Dacjeon：Computational Intelligence in Robotics and Automation，2009：509-514

［9］Chris Harris，Mike Stephens.A combined corner and edge detector［C］／／Proceedings of the 4thAlvey Vision Conference.Machester：University of Machester，1988：147-154

［10］Chris Harris.Geometry from visual motion，active motion［M］.Cambridge：MIT Press，1992：263-284

［11］Zheng Zhiqiang，Wang Han.Analysis of gray level corner detection［J］.Pattern Recognition Letters，1999，20（2）：149-162

［12］R O Duda，P E Hart.Use of the Hough Transformation to detect lines and curves in pictures［J］.Communications of the ACM，1974，15（1）：11-15

［13］孙鹏，吕乃光，王博恩，等.视觉测量中圆型标志点的全场自动识别和提取［J］.北京信息科技大学学报，2011，26（3）：91-95 Sun Peng，Lu Naiguang，Wang Boen，et al.Automatic recognition and extraction of circle marked point in full images of photogrammetry［J］.Journal of Beijing Information Science ＆Technology，2011，26（3）：91-95（in Chinese）

［14］吴迪，吕乃光，邓文怡.大尺寸全视场目标点的自动定位方法［J］.光子学报，2009，38（7）：1826-1829 Wu Di，Lu Naiguang，Deng Wenyi.A method for the automatic location of whole target images in large-scale vision measurement［J］.Acta Photonica Sinica，2009，38（7）：1826-1829（in Chinese）