模块化卫星的多螺杆连接分析

（航天东方红卫星有限公司，北京 100094）

1 引言

模块化卫星是近年提出的一种卫星概念［1］，它由若干结构独立的不同功能模块组成。模块化卫星中的各模块可以并行地加工、测试和试验，与通常的卫星相比，它具有接口简单、研制快捷、便于更换等特点［2］，是一种具有发展前景的小型卫星。

基于以上特点，按模块化思路研制了一个模块化形式的小卫星，模块化小卫星中的各模块结构通过多根螺杆上下贯穿起来成为一个卫星整体，卫星的整体刚度以及能否安全承受外部载荷，很大程度上取决于螺杆的连接设计。因此，模块化卫星的螺杆连接设计与分析具有重要的意义。

螺栓或螺杆连接的设计与分析已有较多的研究［3-8］，其中最重要的是螺栓预紧力的分析，一般通过连接件（即螺栓）与被连接件的载荷与变形关系得到螺栓的预紧力，这种分析一般针对单螺栓的情况。对于多个螺栓，一般假定每个螺栓的载荷变形关系相同或者被连接件具有一样的连接刚度，这样多个螺栓的连接分析简化为单螺栓的计算方法，如文献［9］开展了复杂受力下多个螺栓连接的强度分析，假定被连接板件为绝对刚性，并假定螺栓平均受力，没有考虑多个螺栓处的被连接件刚度的不同及其影响。对于普通的结构被连接件如法兰的螺栓固定连接，各螺栓连接处的被连接件刚度基本相同，一般可按单螺栓情况进行连接分析。对模块化卫星，由于具有多个模块结构，并且每个模块内部结构有所不同，这样整体连接后，各螺杆连接处的被连接件的刚度不尽相同，按每个螺栓平均受力的分析将会产生较大误差，因此不能简化为单螺栓连接的情况。目前，对于连接刚度不均匀的被连接件，连接刚度在螺栓连接强度中的相互耦合作用与影响还很少考虑，有待深入分析与研究。

本文对于模块化卫星多螺杆连接处具有不同连接刚度的情况，在单螺栓载荷分析方法的基础上，推广分析被连接件为非均匀刚度情形下的螺杆直径选取与预紧力大小。

2 模块化卫星构造

模块化卫星由接口尺寸相同、高度可以不同的各模块组成。模块的典型构造如图1所示。一个模块包括一个模块盒和一个电路板。模块盒一般为方形盒式金属薄壁结构，用于承载电路板。模块盒的上下不封闭，可以与其它模块连接。电路板安装在模块盒内，电路板上装有元器件或组件，实现模块的电子功能。

图1 模块构造Fig.1 Module construction

各模块通过螺杆压紧叠摞在一起构成整个卫星，整星构造示意图见图2。模块盒一般四周开有螺孔，螺杆通过螺孔贯穿模块盒。穿过所有模块盒之后，在螺杆的两端拧紧，把各模块固定在一起形成卫星整体。螺杆的长度取决于各模块的高度之和。

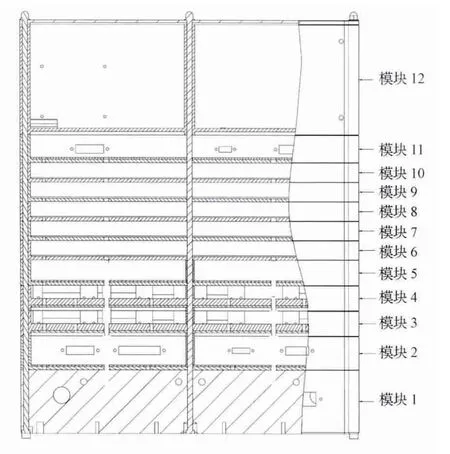
图2 卫星构造示意图Fig.2 Diagram of satellite construction

模块化卫星底部一般通过对接结构连在一个大卫星上或者运载火箭上。模块化卫星所受的载荷主要由紧固螺杆及各模块盒结构来承受。模块化卫星是靠螺杆贯穿连接，螺杆压紧的连接设计是保证模块化卫星整体刚度的重要手段。螺杆连接设计的合理性和正确性的判据是：

沿螺杆连接的纵向，模块间不发生分离，仍处于压紧状态。并且螺杆受力在材料强度容许范围内。

沿螺杆连接的横向，模块间不发生错动，即模块间剪切力小于面间摩擦力。并且螺杆受力在材料强度容许范围内。

3 螺杆连接的纵向分析

3.1 各螺杆处卫星结构的连接刚度系数

对第一个螺杆施加拧紧力矩则产生一定的预紧力P1，则在本螺杆和其他螺杆处，卫星结构都会产生压缩位移，记为x11、x12、x13，…，x1j（第一个螺杆的力在第j螺杆处的位移）。因此，第i个螺杆的力在第j螺杆处的位移为xij（i＝1，2，…，n；j＝1，2，…，n；n为螺杆的数量）。xij可以通过有限元法计算得到。模块化卫星的有限元分析可以按连续结构进行建模（不包括螺杆），分别在对应每一个螺杆两端的卫星结构模型上施加作用力Pi（可取任意确定的值，如取一个单位载荷值），计算出压缩位移xij，则

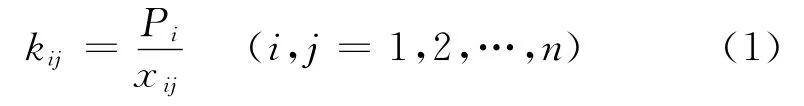
式中：kij为i螺杆在j螺杆安装处的卫星结构刚度系数；kii为i螺杆在本身螺杆处的卫星结构刚度系数。

3.2 外载荷下卫星结构的拉伸位移

一般在卫星设计中把静、动态载荷等价为准静态载荷（纵向Fq，横向Fh）进行计算。卫星在纵向准静态载荷Fq的主导作用下会产生拉伸位移，此时只分析准静态载荷对卫星结构的作用而暂不考虑对螺杆的影响（下一步考虑）。采用上述同样的卫星结构有限元模型，计算准静态载荷作用下对应于各螺杆两端的卫星结构上拉伸位移ai。

3.3 外载荷下各螺杆的附加拉伸力

准静态载荷对卫星结构产生拉伸位移ai，也会对螺杆产生作用，因此各螺杆在原来拉伸力基础上产生附加的拉伸力，记为Fi。在Fi作用下，各螺杆产生附加拉伸位移为ui，对于卫星结构来说，卫星结构承受与Fi同样大小的压缩力，其产生的附加压缩位移记为vi。根据螺杆与卫星结构之间的变形协调关系，可以得出

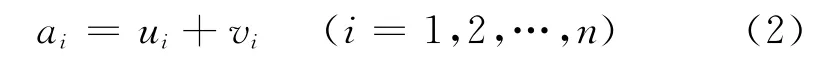
对于螺杆来说，如螺杆的截面积为A，长为L，材料弹性模量为E，则

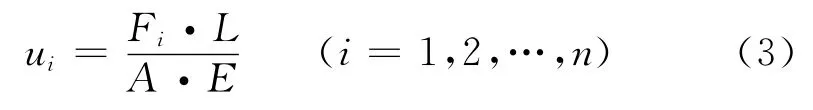
在与Fi等价的压缩力作用下，卫星结构产生的压缩位移可用一般式表示为

于是有

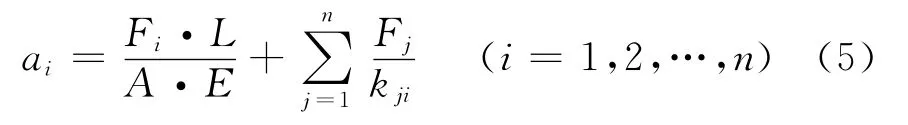
给定卫星准静态载荷，可以计算得到ai。式（5）为Fi的方程组，ai、kij为已知量，螺杆的材料、尺寸确定时，可以求解得到各螺杆附加拉伸力Fi，相应位移ui、vi可以确定。

在各螺杆分散分布的情况下，vi的位移主要产生于kii，即kii刚度系数起主要作用。因此，根据式（5），忽略kij（i≠j），可以得到求解Fi的简化式：

3.4 压紧螺杆直径确定

对于所有n个螺杆，若施加相同的预紧力P，卫星结构由此产生的压缩位移为δi。δi是对应第i个螺杆处的卫星结构压缩位移。

安全情况下，卫星结构在外部载荷作用下仍应处于压缩状态，即有

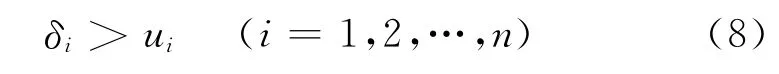
即

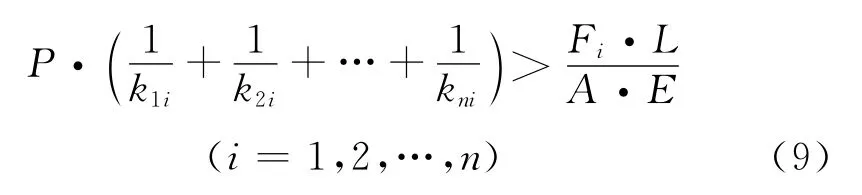
由上式可以确定需要的预紧力P

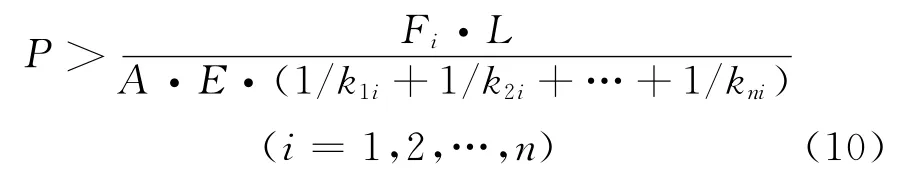
取1.5的安全系数，则

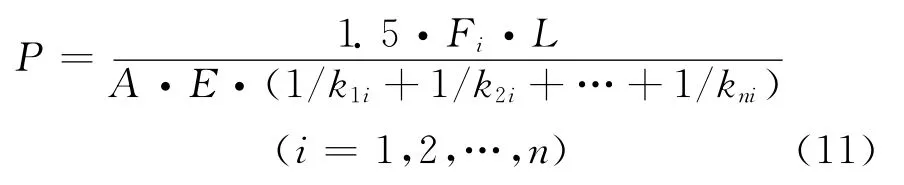
如果忽略kij（i≠j），只考虑kii的作用，则螺杆拧紧产生预紧力为

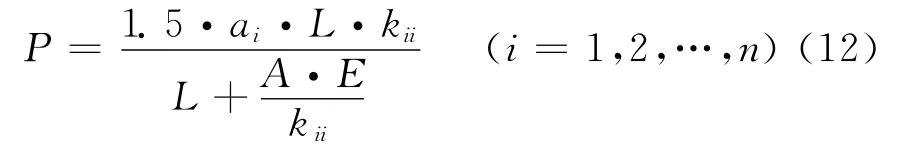
此时，每个螺杆受到总拉力为

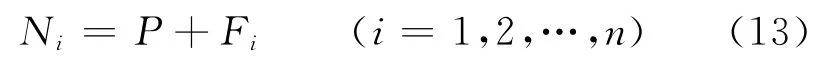
螺杆受到拉伸力Ni作用产生的应力为

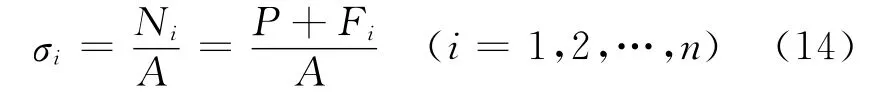
如果螺杆材料的拉伸强度为σb，取1.5倍的安全系数，则螺杆的许用应力为

按照强度设计理论，螺杆上的应力应小于螺杆的许用应力，即

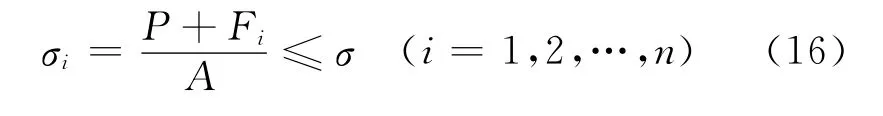
把式（6）和式（12）代入式（16），得到

求解得到螺杆截面积

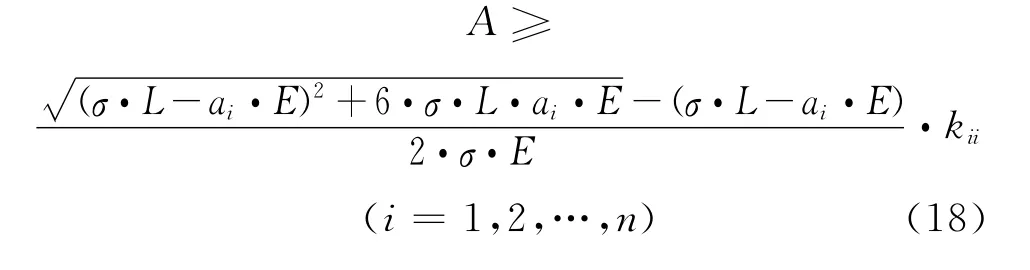
由式（18）计算得到螺杆最小截面积A，再依据截面积A求出最小螺杆直径D。根据最小螺杆直径D，可以按螺纹标准目录选择满足最小螺杆直径的标准螺杆直径。

4 螺杆连接的横向分析

4.1 受力状态

在外载荷作用下，卫星各模块间将产生剪切力，如果卫星模块接触面间的摩擦力较小，则外载荷带来的剪切力将超过卫星模块面间的摩擦力，从而引起卫星模块间的错动，破坏卫星的主体结构。因此，施加螺杆预紧力的大小要足以保证模块接触面间的摩擦力大于外载荷引起的模块间剪切力，避免模块间的错动。

4.2 模块间界面剪切力

在外部准静态载荷的作用下，可以通过有限元分析计算，得到各模块间的总剪切力Ft。

式中：p指第p个卫星模块的接触面，Qpq为沿第p个接触面的各面单元的剪切力，m为第p个接触面的建模得到的面单元数量，bpq为各单元长度。尽管各模块接触面的横剪切力都应利用上式计算得到，但一般在横向力的作用下，最底部接触面的横剪力最大，因此，一般只需计算最底部模块接触面的横剪力。不同的有限元建模，单元划分不同，单元的长度、大小可能不同，相应地不同建模中单元的剪切力不同，但只要建模中单元按规范划分，最终计算得到的接触面总剪切力是接近的，可以满足使用要求。

4.3 模块间摩擦力

各螺杆施加相同的拧紧力矩，产生的预紧力为P，在纵向载荷的作用下，螺杆上力会产生变化，变化的大小为Fi，由式（6）确定。因此，卫星模块受到的总的压紧力为

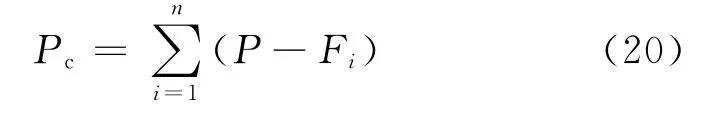
若接触面间的摩擦系数为f，则接触面间的摩擦力为

为避免模块间的错动，模块间的总剪切力Ft必须小于模块间的摩擦力，即

把式（20）代入得到

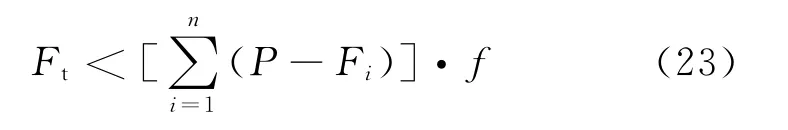
4.4 压紧螺杆直径确定

对于n个螺杆，根据式（23），需要的螺杆预紧力为

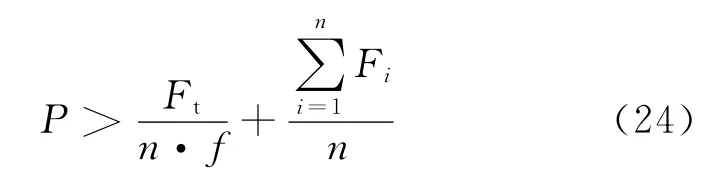
根据螺杆上应力应小于螺杆许用应力的原则，考虑1.5倍的系数，得到

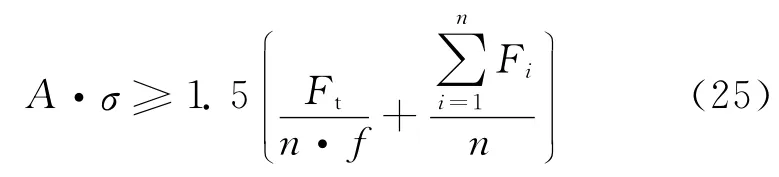
把式（6）代入式（25），可得

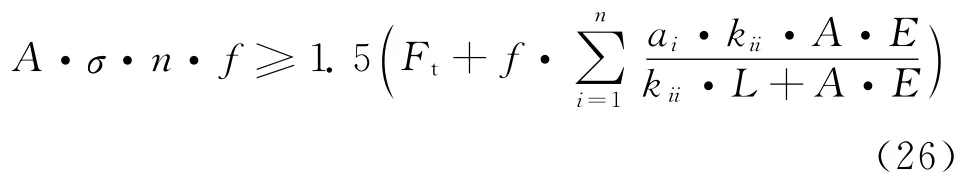
根据式（26）可求螺杆最小截面积A，求出最小螺杆直径D。根据最小螺杆直径D，按螺纹标准目录选择满足最小螺杆直径的标准螺杆直径。

在AE远小于kiiL的情况下，式（26）可以简化为

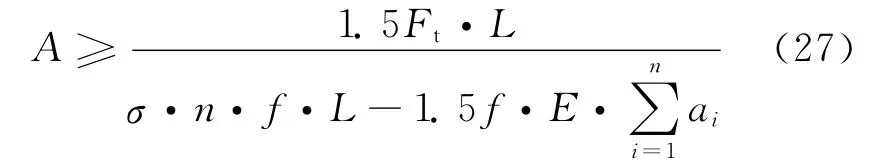
最后，综合横向和纵向分析计算的结果，选取满足横向和纵向两种分析情况的螺杆参数最大值。

5 模块化卫星螺杆参数的计算实例

5.1 初始条件

一个模块化小卫星利用对接环固定于另一个较大卫星的顶部，模块化卫星承受纵向16gn和横向5gn准静态设计载荷，本文对此模块化小卫星按纵向和横向分别进行螺杆的连接分析。

模块化小卫星设计使用9根螺杆，螺杆材料为钛合金，材料弹性模量E为1.1×1011Pa，根据模块卫星高度，螺杆有效长度L为486.5mm。9根螺杆中的8根沿卫星四周均匀分布，第9根从卫星中心穿过。9根螺杆自卫星一角处开始，以卫星中心螺杆为结束，逆时针顺序进行标号，分别编为螺杆1、螺杆2、螺杆3、螺杆4、螺杆5、螺杆6、螺杆7、螺杆8和螺杆9。

卫星模块盒结构为四方形结构，壁厚为3mm，尺寸为400mm×320mm，材料为铝合金，模块高度和为486.5mm。按连续结构，建立卫星有限元模型。

5.2 纵向分析计算

纵向16gn和横向5gn准静态力作用下，通过有限元分析得到9个螺杆处卫星结构的纵向位移大小如表1所示。

表1 准静态力下结构位移Table 1 Displacements of satellite structure under quasi-loads

分别在卫星上每个螺杆处施加相同的单位压紧力P，通过卫星有限元模型，计算得到位移xij（i＝1，2，…，9；j＝1，2，…，9）。根据式（1），由位移xij和单位压紧力可以计算得到刚度系数（单位为N／m）

可以看到，在各螺杆相距不太近的情况下，kij（i≠j）远大于kii，即刚度系数矩阵对角线具有较小的值。从计算位移来看，kii得到相对较大的位移，是kij对应位移的几十倍之上，因此，只取kii进行位移计算已经足够。

螺杆材料拉伸强度σb＝6.8×108Pa，根据式（18），得到满足要求的最小螺杆直径为2.2 mm。根据螺纹标准，可选择螺杆M3。

5.3 横向分析计算

对卫星施加纵向16gn和横向5gn准静态力，进行有限元应力分析，分析计算显示底部剪切力较大，因此，以卫星底部模块为例分析模块间的剪切力。

卫星底部模块为方形盒，中间有二个交叉隔板，因此共有6块板。有限单元分析得到的各板面在接触面的剪切力和总剪切力见表2。

对于直径几个毫米的螺杆，可以看到kiiL比AE大1～2量级，因此，可以按照式（27）计算螺杆参数。接触面的摩擦系数按保守原则取为0.3，计算得到最小螺杆直径为1.95mm。根据螺纹标准，可选择螺杆M3。

表2 底部模块各板面的沿接触面剪切力FtTable 2 Shear forces in bottom module N

5.4 最终螺杆直径的确定

综合考虑纵向和横向下的计算结果，此模块化卫星的压紧螺杆直径选取M3。

5.5 螺杆预紧力

按M3螺杆，其截面积A为7.065×10-6mm3。在纵向分析中，根据式（12）得到最小预紧力315N。在横向分析中，根据式（24）得到最小预紧力906N。综合考虑，螺杆的预紧力选为1500N。在螺杆1500N预紧力下，利用式（16）验证螺杆的使用安全。M3螺杆上最大应力根据式（16）算得为233MPa，小于螺杆许用应力680MPa，满足螺杆强度要求。

根据螺纹连接的理论［10］，拧紧力矩T与预紧力P有如下的关系：

式中：D为螺杆直径，c为拧紧力矩系数，一般取为0.2。

因此，计算得到螺杆的拧紧力矩T＝1Nm。

6 结论

在单螺栓的载荷分析的基础上，通过计算被连接件的刚度矩阵参数，把被连接件的刚度矩阵参数与多螺杆载荷分析相结合，推导得到了计算螺杆直径与预紧力的公式。模块化卫星的多螺杆连接算例表明，这种方法可以应用于模块化卫星的连接计算。

（References）

［1］Wegner P M，Blower P，Wilkenfeld J.Standard buses，modular buses，and plug-and-play buses：what is the difference and why does it matter？［C］／／Proceedings of the 4SSymposium-Small Satellites System and Services.Noordwijk.Netherlands：ESA-ESTEC，2008

［2］Mostert S，Steyn H，Burger H，et al.Sumbandilasat-an operational technology demonstrator［J］.Acta Astronantica，2008，63：1273-1282

［3］山本晃.螺纹连接的理论与计算［M］.上海：上海科技文献出版社.1984 Shanben Huang，Theory and computation of thread connection［M］.Shanghai：Shanghai Scientific Document Press，1984（in Chinese）

［4］卜炎.螺纹连接设计与计算［M］.北京：高等教育出版社，1995 BuYan.Design and computation of thread connection［M］.Beijing：High Education Press，1995 （in Chinese）

［5］李至广.钛合金螺纹连接结构预紧力、应力、可靠性分析［D］.长沙：国防科学技术大学，2004 Li Zhiguang.Preload stress and reliability analysis for titanium screw joint structure［D］.Changsha：National University of Defense Technology，2004（in Chinese）

［6］陈烈民.航天器结构与机构［M］.北京：中国科学技术出版社，2005 Chen Liemin.Spacecraft structures and mechaniom［M］.Beijing：Chinese Science and Technolgy Press，2005（in Chinese）

［7］吴宇.法兰连接中螺栓预紧力及垫片密封性的研究［J］.炼油技术与工程，2006，36（7）：45-48 Wu Yu.Study on pre-tightening force of bolts in flange connection and sealing performance of gasket［J］.Petroleum Refinery Engineering，2006，36（7）：45-48 （in Chinese）

［8］周坤，刘美红.法兰螺栓连接中螺栓预紧力的计算和控制方法分析［J］.新技术新工艺，2010（8）：26-28 Zhou Kun，Liu Meihong.Analysis of calculation and control methods of the bolt preload in the flange bolts connection［J］.New Technology ＆ New Process，2010（8）：26-28（in Chinese）

［9］苏德利，刘文顺，孙久艳.普通螺栓连接在复杂受力下的强度分析［J］.河南城建学院学报，2011，20（4）：16-18 Su Deli，Liu Wenshun，Sun Jiuyan.The strength analysis of common bolt fastening in complex carrying ability［J］.Journal of Henan University of Urban Construction，2011，20（4）：16-18（in Chinese）

［10］成大先.机械设计手册，第二卷［M］.北京：化学工业出版社，2007 Cheng Daxian.Handbook of mechanical design，Volume 2［M］.Beijing：Chemical Industry Press，2007（in Chinese）