耦合网络边相继故障模型研究

王建伟，蒋 晨，孙恩慧

东北大学 工商管理学院，沈阳 110819

耦合网络边相继故障模型研究

王建伟，蒋 晨，孙恩慧

东北大学 工商管理学院，沈阳 110819

针对耦合网络上频发的相继故障问题，通过分析边级联故障蔓延的动力学演化机制，构建耦合网络上边相继故障模型。以提高耦合网络整体抵制相继故障能力为出发点，依据不同度量指标，多角度分析具有不同耦合模式的耦合网络鲁棒性与模型参数之间的关联性，研究耦合网络间耦合模式和网络基本模型等因素对相继故障的影响，探讨耦合网络边相继故障模型的整体保护策略。研究结果表明，同配连接模式能够增强耦合网络抵制级联故障的鲁棒性；相互依赖的两个耦合网络之间拓扑结构越相似，网络抵制相继故障的鲁棒性越强；耦合网络鲁棒性与网络平均度正相关；适当的增加耦合网络间对称边数量，能够有效提高网络的鲁棒性。最后，应用边相继故障模型在耦合电力网络上进行实例分析。

相继故障；耦合网络；连接模式；鲁棒性

1 引言

近年来，国内外突发事件频繁发生，如意大利大停电事故、禽流感病毒传播、松花江水污染、印度洋海啸、金融危机等，这些事件都可以看作是相继故障引发的灾难。大规模相继故障一旦发生，往往会给国家造成严重的经济损失，也会对人们生活带来诸多不利的影响。为应对相继故障引发的各种灾难，国内外学者展开了广泛的研究。已有对相继故障领域的研究主要聚焦在单层次网络上，但通过对2003年意大利停电事故导致互联网瘫痪以及2012年印度断电事故导致一系列连锁灾害等突发事件的验证发现，许多关键网络系统上发生的相继故障灾难大多是由于网络间具有耦合作用关系导致的。在耦合网络中，一层网络上出现微小的故障，可能导致多层相互依赖的网络间发生故障的连锁反应。并且，许多关于耦合网络相继故障模型的研究中仅考虑网络节点的行为，忽略了边在相继故障蔓延中的作用。另外，由于耦合网络的研究起步较晚，对于控制相继故障发生、提高网络鲁棒性等方面尚未进行充分的研究，虽然仅仅依靠单层次网络上相继故障模型来探讨有效的预防策略有一定的作用，但这个框架与一个能正常运转的系统还有很大的差距。

基于此，本研究选取耦合网络作为研究对象，从边的角度建立相继故障模型，基于模型给出有效的保护策略，为指导现实网络系统的构建提供借鉴和参考。

2 相关研究评述

相继故障现象普遍发生在许多关键的基础设施网络中，如电力网络上的大规模停电事故[1]、交通网络中的大范围拥堵现象[2]、Internet网络上计算机病毒传播[3]等。为此，许多学者针对相继故障问题展开大量的研究，并得到许多有价值的结论，通过对相继故障理论的研究，能够合理地解释现实生活中重大灾难的演化机制。有关复杂网络相继故障的研究大多是从节点属性的角度建立模型，最早的研究是基于网络介数建立负荷容量模型。Motter等[4]研究发现，无标度网络结构的异质性导致网络负荷分布的极度不均匀，是呈现的脆弱性的关键所在；Zhao等[5]通过分析影响网络鲁棒性的临界点，提出有效地预防无标度网络节点大规模连锁崩溃的保护措施。然而，计算介数必须要了解网络的全局信息，由于一些现实的网络系统规模庞大、结构复杂，很难获取全局信息。针对于此，Zheng等[6]从网络拥塞的角度提出节点负荷新的定义方式，并对导致相继故障发生的一系列影响因素展开详细分析；任俊亮等[7]基于节点剩余容量的负载重分策略，建立了一个无标度网络的相继故障模型；Cao等[8]基于节点度函数和超负荷节点局域择优重新分配原则建立相继故障模型。为了有效解决实际问题，王皓[9]构建Web服务交互网络演化模型，基于两种引发相继故障的策略，研究服务网络的相继故障现象；陈星光等[10]构建城市交通系统的耦合映像格子模型，利用该模型研究城市交通系统的相继故障问题；宋毅等[11]研究相继故障的时序问题，构建了具有时序特征的相继故障演化模型。为提高网络的鲁棒性，朱凌峰等[12]基于节点有效路径的路由策略进行改进，能够在基本不增加网络数据包平均传输延时的基础上有效地提高网络吞吐量；段东立等[13]分析过载机制下节点重要度的演化机理，即非关键节点如何演化成影响网络级联故障行为的关键节点；Tessone等[14]从网络节点能力临界参数的角度，建立相继故障模型，通过赋予节点能力一定的安全阈值，实现有效地降低故障连锁反应对网络造成灾难性的破坏。

在关注网络节点属性的同时，许多学者也从边的角度展开探讨，Holme[15]基于边的介数定义节点负荷；Wang等[16]根据加权流局域分配的原则，建立边相继故障负荷-容量模型，研究发现，网络中起传输作用的边同样在相继故障中占据着举足轻重的地位。

实际上，许多关键生命线系统网络中大规模相继故障的发生往往是由多网络间具有相互耦合的关系所导致的，如2003年意大利发生的互联网与电力网络相互影响导致的近乎全国性的断电事件(只有西西里幸免)以及互联网瘫痪事件。Buldyrev等[17]基于意大利真实的地理位置，模拟2003年爆发在电力网-计算机耦合网络上的相继故障现象，解释了由于1个供电站失效导致的近乎全国性的大规模停电和互联网瘫痪事件，从耦合网络的角度分析多层网络间大规模相继故障的发生原因，并阐述了许多大规模灾难不仅仅是相继故障在单层网络上蔓延扩散的事实情况，开辟了有关耦合网络领域的研究先河。之后，Parshani等[18]、Shao等[19]在Buldyrev等[17]研究的基础上，突破已有耦合网络研究体系的局限，提出基于网络间局部随机耦合的理论研究框架，探讨网络间局部耦合的两层次网络模型的鲁棒性，并得到许多有价值的结论。

有关耦合网络相关性质的研究，许多已有的成果都是基于渗流理论展开的。Buldyrev等[17]最早关注两个相互依赖网络遭遇相继故障的渗流变化过程；Hu等[20]也应用渗流理论研究耦合网络的鲁棒性，发现渗流曲线呈现一阶和二阶混合过渡的变化过程是由于网络间存在相互依赖的连边所致；Dong等[21]应用渗流理论研究局部耦合的加权网络遭遇蓄意袭击的鲁棒性；李稳国等[22]分析边攻击下的相互依赖网络相继故障渗流及其结果。在两层次耦合网络的基础上，部分学者针对多层耦合网络上发生的相继故障研究渗流曲线的变化规律，Gao等[23]探讨树型和环型的多层耦合网络，Dong等[24]研究树型全局耦合和星型局部耦合的多层网络模型。广泛应用于物理和数学领域的渗流理论也适用于复杂网络相关的研究，能够诠释网络系统的稳定性和脆弱性，分析袭击策略的有效性，并预测渗流临界值等。

耦合网络的研究起步较晚，在2010年以前，有关相继故障理论的研究和应用主要聚焦在单层次网络。而许多关于耦合网络相继故障模型的研究中，仅考虑网络节点上的行为，而忽略了网络中连接两个节点之间的边扮演的重要角色，并且有关应用领域的研究尚未充分展开。本研究重点分析边在耦合网络相继故障繁衍中扮演的角色，通过详细分析耦合网络上相继故障的动力学演化机制，提出耦合网络上边相继故障模型；依据提出的几种度量网络鲁棒性的指标，研究耦合网络间的耦合连接模式和网络拓扑结构对网络鲁棒性的影响，给出抵制相继故障最稳健的耦合网络架构以及耦合网络上整体的保护措施。

3 相继故障模型

在建立耦合网络的相继故障模型时，仅关注由两个网络构成的相互依赖耦合网络，即网络A和网络B，定义两个网络具有相同的网络规模，且网络A中的节点与网络B中的节点一一对应，相互依赖。如果网络A中的1个节点失效，将导致与之相互依赖的网络B中的节点也随之失效；反之，如果网络B中的1个节点失效，将导致与之相互依赖的网络A中的节点也失效。

耦合网络上相继故障的蔓延过程如图1所示，初始阶段网络中没有节点和边的失效，图中实心的节点表示正常的节点，空心的节点表示失效的节点，虚线表示即将要失效的边。图1(a)中，当网络中的边A3A5由于人为的袭击或移除(图中attack)导致失效，网络A分裂成两个独立的团体，在每个团体内部所有节点都是健康的并相互连通，将这种团体称之为功能团，那么网络A分裂成为两个不同的功能团，分别是节点{A1、A2、A3}所在的功能团和节点{A4、A5、A6、A7}所在的功能团。依据Buldyrev等[17]对耦合网络上功能团的定义方式，下一阶段网络B也将分裂成与网络A一一对应的相互独立的功能团，连接在两个功能团上的所有连边B3B4、B1B5随之失效，如图1(b)所示。此时的网络B分裂成3个不同的功能团{B1、B2}、{B3}、{B4、B5、B6、B7}，节点B3分裂成孤立的节点，节点B3失效，网络A与网络B之间的连边A3↔B3随之断开(图中×)；B3通过A↔B耦合在网络A的节点A3随之失效，与节点A3相连的所有连接也相继失效，如图1(c)所示。图1(d)为没有相继故障的蔓延，网络最终的稳定状态。当网络最终达到稳定状态时可能会出现很多种情况，如包含N(N≥0)个功能团，但是只有最大的功能团才是被关注的。

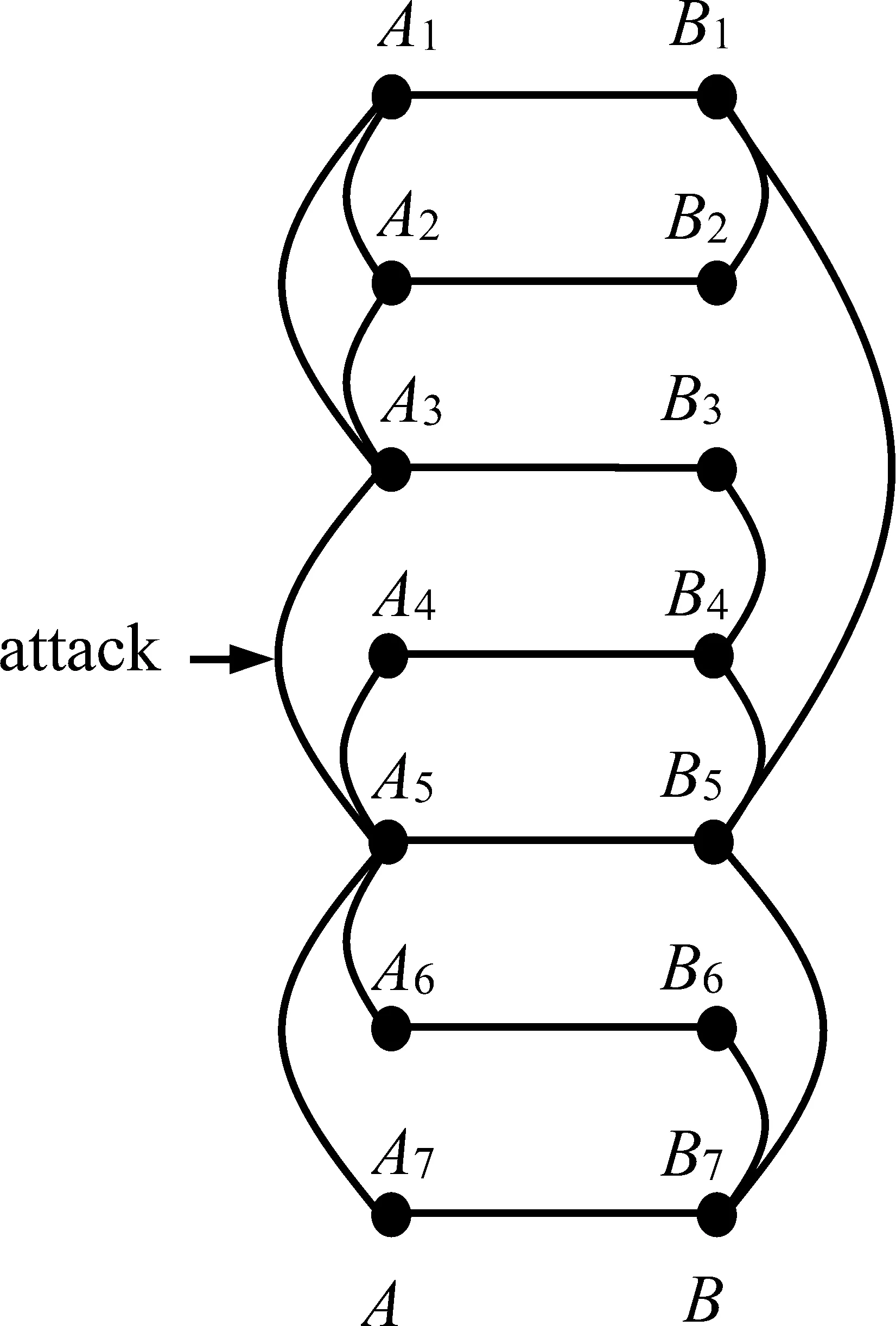
(a) (b) (c) (d)

图1相继故障在耦合网络上传播过程
Figure1PropagationProcessofCascadingFailuresinCoupledNetworks

网络A中的部分节点和网络B中的部分节点分别记为集合a和集合b，称集合a和b构成耦合网络上彼此相互连接的最大功能团，当且仅当满足以下条件。①集合a中的节点与集合b中的节点之间一一对应、相互耦合；②集合a中的所有节点之间能够通过某种连边路径彼此相互连通；③集合b中的所有节点之间能通过某种连边路径彼此相互连通；④耦合网络上都不能再增加其他相互耦合的节点来满足上述所有条件，则称集合a和b构成耦合网络上彼此相互连接的功能团。在耦合网络上，只有彼此相连的功能团才能发挥潜在的功能。满足上述所有条件的彼此相互连接的功能团可能不止1个，如果满足上述所有条件外，也满足⑤该相互连接的功能团相比耦合网络上其他的相互连接的功能团拥有最多的节点数量。根据上述对耦合网络功能团的定义，图1(d)中节点A4所在的彼此相连的功能团为耦合网络中最大的功能团。

4 耦合网络模型

4.1 网络模型选择

为了更好地研究影响耦合网络鲁棒性的因素，构建出合理的耦合网络模型至关重要。在本研究中，网络基本拓扑模型的选择主要聚焦于两种经典的网络模型，即BA无标度网络模型[25]和ER随机网络模型[26]。在构建BA网络时，设定参数值m=2，m0=3，网络节点数N=5 000。依据BA网络模型原理可知，生产的BA网络的平均度〈k〉=2m，即网络的平均度〈k〉=4。在构建ER网络时，设定模型中参数p=0.0008，网络节点数N=5 000，网络的平均度〈k〉≈4。

4.2 网络间耦合模式设计

耦合网络的拓扑结构对相继故障的动力学过程起着至关重要的作用，对于1个给定的基本网络模型(BA无标度网络或ER随机网络)，耦合网络拓扑结构的不同主要取决于两层网络之间连接模式的差异。本研究在构建相互依赖的耦合网络模型时，主要采用随机连接、同配连接和异配连接3种不同的耦合连接模式。

(1)随机连接(random link, RL)。网络A中的节点随机连接网络B中的节点，并构成两个网络节点间一对一的连接模式。

(2)同配连接(assortative link, AL)。网络A中节点和网络B中的节点按照节点度大小连接，即网络A中度大的节点连接网络B中度大的节点，并构成两个网络节点间一对一的连接模式。

(3)异配连接(disassortative link, DL)。与同配连接相反，网络A中度大的节点连接网络B中度小的节点，并构成两个网络节点间一对一的连接模式。

5 耦合网络抵制边相继故障的鲁棒性分析

5.1 度量指标的确定

为了更好地研究耦合网络上的相继故障现象，更全面地量化网络整体抵制相继故障的能力，从全局性角度衡量整个耦合网络的鲁棒性，提出4种度量指标。

(1)失效节点归一化指标S。在耦合网络边的相继故障模型中，边的失效可能会导致网络中节点失效，指标S表示网络中失效节点的数量占网络所有节点数量的比重。通过计算网络中边的失效导致失效节点的数量，能够度量网络抵制相继故障的稳定性。计算公式为

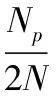
(1)

其中，p为网络中移除的边占全部边的数量的比例，Np为移除比例为p的边以后失效节点的数量，N为一个单层次网络中节点的总数。

(2)耦合网络失效点数量占单层网络的比例p(s)。为了更好的对比不同的耦合连接模式对网络鲁棒性的影响，并对比相继故障对单层次网络的影响，以建立最优的抵制相继故障的耦合网络架构。p(s)表示耦合网络相比单层网络所增加的额外脆弱程度，即

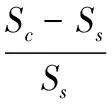
(2)

其中，Sc为耦合网络失效节点的总数，Ss为单层次网络失效节点的数量。

(3)失效边归一化指标F。计算移除比例为p的边后所导致网络中其他边失效的数量f，0≤f≤N(1-p)。由于选择进行数值模拟的耦合网络具有不同的连边数量，为了量化整个网络抵制相继故障的鲁棒性，采用失效边的归一化指标，即

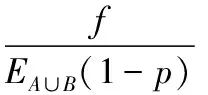
(3)

其中，EA∪B为耦合网络上所有连边数量和。

(4)衡量耦合网络连通性的归一化指标P∞。基于赵月[2]对度量指标P∞的定义，P∞为移除比例为p的连边引发的网络上相继故障蔓延结束后，随机选取1条边，这条边包含在最大功能团中的概率，0≤P∞≤1。在耦合网络中，只有彼此相互连通的功能团才具有研究意义。因此，无相继故障蔓延后剩余的最大功能团代表着耦合网络中能够发挥效用的最大功能团，最大功能团中节点的数量越多，说明网络仍可保持基本的连通性。如果在移走少量边后，耦合网络之间绝大部分的节点仍然能通过网络中存在的边相互连通，那么则称该网络的连通性对抵制故障具有鲁棒性。因此，P∞的值与网络的鲁棒性之间正相关，即P∞值越大，网络抵制相继故障的能力越强，反之网络越脆弱。

5.2 无标度网络的对比分析

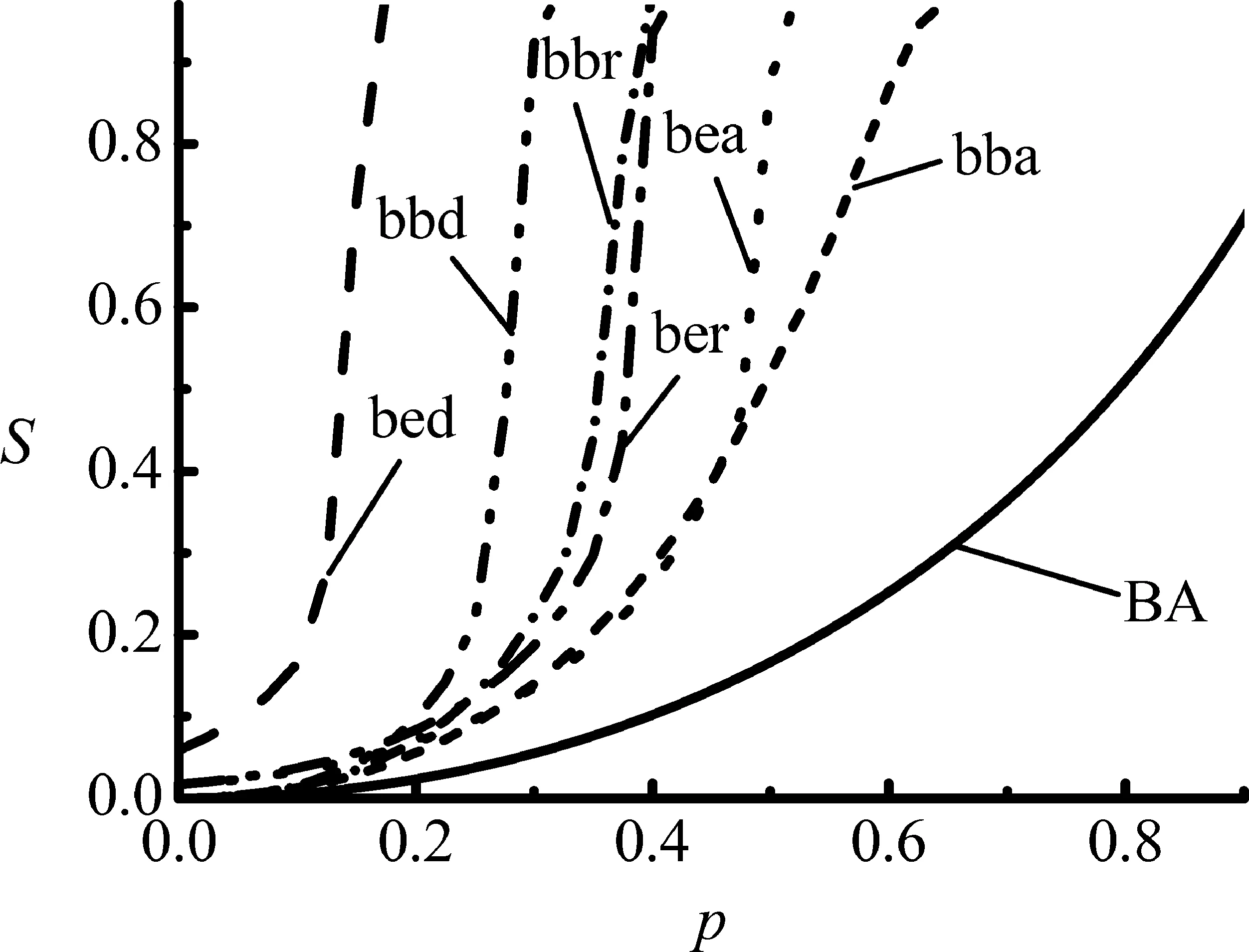
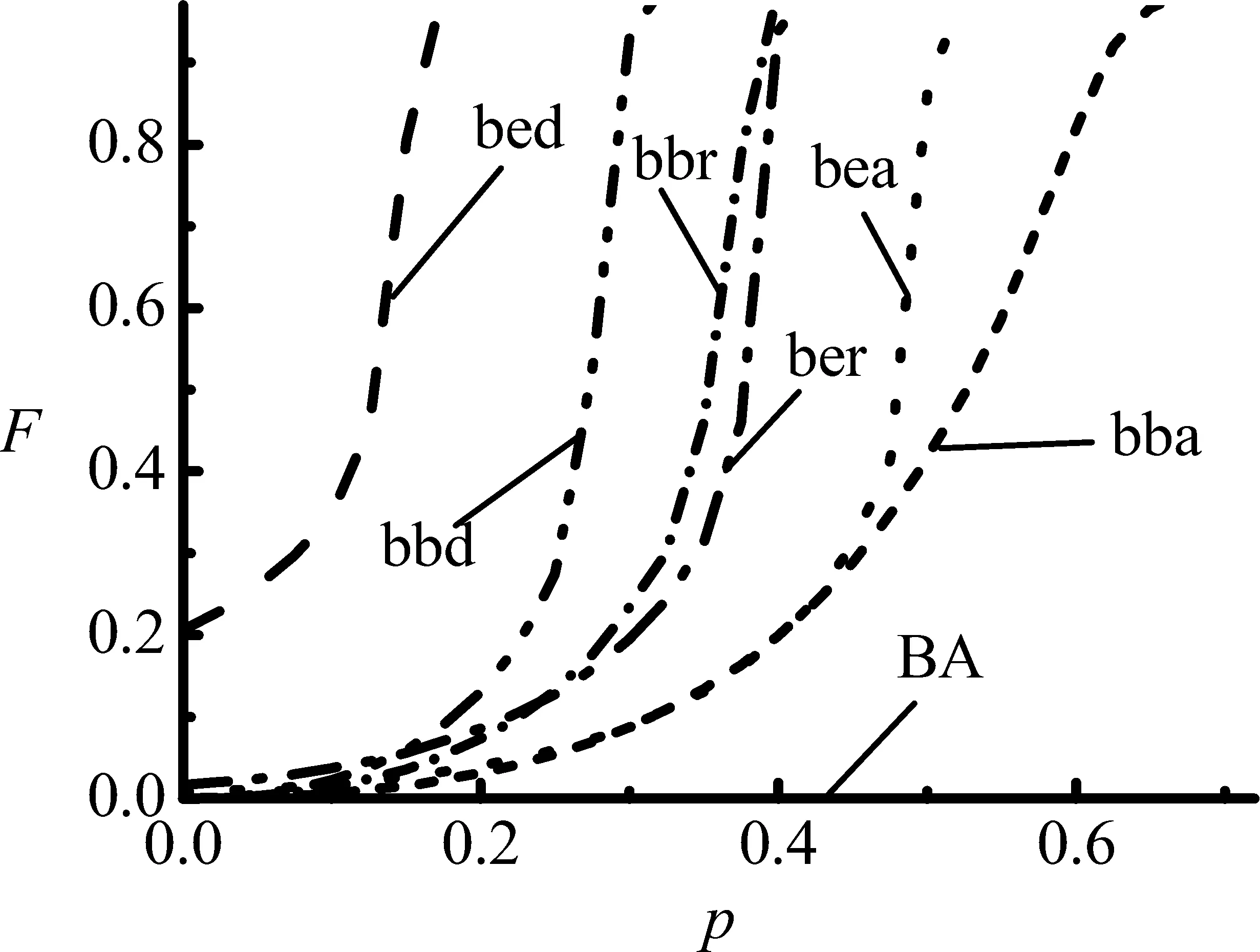
选择BA无标度网络作为研究对象，对比分析由BA网络构成的耦合网络上相继故障的蔓延情况，构建6种不同的耦合网络架构，分别为BA-BA(RL)、BA-BA(AL)、BA-BA(DL)、BA-ER(RL)、BA-ER(AL)和BA-ER(DL)，两层次相互依赖的耦合网络模型在数值模拟图中简写为bbr、bba、bbd、ber、bea和bed；对比单层BA网络，所有采用的网络规模N=5 000，平均度〈k〉≈4。

本研究模拟了6种不同架构的耦合网络与单层BA网络在移除比例为p的连边，即移除E·p数量的连边后引发相继故障的蔓延结果(E为网络边数量)，并使用失效节点归一化S、失效点比例p(s)、失效边归一化指标F和P∞共4种度量指标量化网络抵制相继故障的鲁棒性。数值模拟结果如图2所示，图中每条曲线的模拟结果都是20个不同耦合网络上相继故障数值模拟的平均结果。

(a) (b)

(c) (d)

图2不同连接模式下耦合网络模型与BA单层网络的对比
Figure2ComparisonbetweenCoupledNetworksandSingleBANetworkwithDifferentLinkPatterns

图2给出6种不同的耦合网络模型与单层BA网络的失效节点数量对比情况。依据各度量指标的定义，失效节点归一化值S和失效的边归一化指标F值越小，网络的鲁棒性越强；失效点比例p(s)值和P∞值越大，网络的鲁棒性越强。因此，从图2(a)中能够看出，由BA网络组成的耦合网络相比单层BA网络更易导致相继故障的蔓延，并且抵制相继故障蔓延的最优耦合网络架构的排列顺序依次为BA-BA(AL)>BA-ER(AL)>BA-ER(RL)>BA-BA(RL)>BA-BA(DL)>BA-ER (DL)。为了进一步对比6种不同的耦合网络模型相比单层BA网络模型增加的脆弱程度，本研究采用网络增加的失效点比例p(s)度量指标量化耦合网络增加的脆弱性，数值模拟的结果如图2(b)所示。由图2(b)可以看出，BA-ER(DL)比其他耦合网络更易导致相继故障大面积的蔓延，而BA-BA(AL)是所有耦合网络中抵制相继故障蔓延的最稳健的耦合网络架构。3种连接模式下，BA-ER耦合网络在移除比例p值很小时，网络的p(s)指标值出现异常的原因如下。①对于网络规模N=5 000的ER随机网络，在平均度〈k〉≈4时，模型参数p=0.0008，此时ER随机网络可能会出现孤立的节点或网络不完全连通等不确定性因素。对于耦合网络来讲，只有彼此相连的功能团才能发挥作用，耦合在一起的BA-ER耦合网络，由于ER随机网络在结构上的不确定性，会使耦合的BA网络中连接于两个不同功能团间的连边失效，基于此，即使对于较小的p值(p<0.100)，BA-ER耦合网络也会表现出异常的脆弱性。②BA网络一个基本的特征在于网络中度分布的不均匀性，网络中存在少量的节点拥有特别大的度，而模型中的ER网络又可能会存在孤立的节点或分散的功能团，BA-ER耦合网络在异配连接DL模式下，使BA网络中度大的节点与ER网络中度小的节点相耦合，甚至可能会导致BA网络中度最大的几个节点连接ER网络中度为零的节点，这样，当p=0时，相比其他耦合网络和BA单层网络，BA-ER(DL)会出现异常大的失效节点和失效边。

网络抵制边相继故障的鲁棒性在基于失效边的归一化指标F与参数p的关系曲线对比中可得出与失效节点指标模拟下相同的结论，如图2(c)所示。当p=0时(不移除网络中的连边)，BA-ER耦合网络会存在失效边，是因为在ER网络中可能存在孤立的节点或不完全连通的功能团。在图2(d)中，由数值模拟结果可知，随着p值的增加，P∞呈现渗流变化的过程，其中存在一个明显的相变点pc(即曲线与横坐标的交点)，当ppc时，网络中几乎不存在较大的功能团。pc值与网络抵制相继故障的鲁棒性呈正相关关系，pc值越大，网络鲁棒性越强；反之，网络越脆弱。根据相变点pc值的大小也可得出最优耦合网络架构的排列顺序依次为BA-BA(AL)>BA-ER(AL)>BA-ER(RL)>BA-BA(RL)>BA-BA(DL)>BA-ER (DL)。

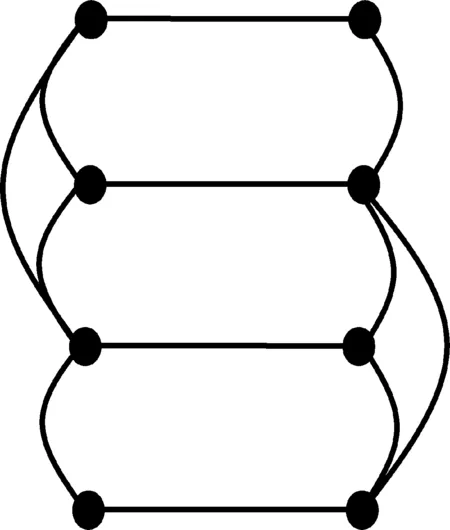
从图2可以看出，相比其他5个耦合网络结构，BA-BA(AL)耦合网络表现出更强的鲁棒性，产生这种现象的原因可能是，对于BA无标度网络，网络中存在少量度特别大的节点，而最大度与最小度之间又存在很大的差异，同配连接AL模式能够减少耦合网络之间连接节点度之间的差异性，并且相同拓扑结构的网络耦合在一起，耦合网络中对称连边数量最多，网络之间结构越相似，使两个网络在移除连边后导致相继故障蔓延的结果更加相似，对网络造成的破坏性也就相对减弱。为了比较直观地了解耦合网络中的对称边在抵制相继故障中的作用，通过对比两个具有不同数量的对称边的耦合网络模型进行解释。图3给出对称边对耦合网络抵制相继故障鲁棒性的作用，图3(a)中的耦合网络比图3(b)中的耦合网络具有更多数量的对称边，图3(a)中的耦合网络有3组对称边，图3(b)中的耦合网络有1组对称边，对称边的数量越多，两层网络越相似，耦合网络结构越稳定，当移除图3(a)中的耦合网络的1条边时，可能不会影响网络整体的连通性，而移除图3(b)中的耦合网络的1条边可能会导致整个网络的崩溃。

(a) (b)

图3对称边对耦合网络抵制相继故障鲁棒性的作用
Figure3InfluenceofSymmetricEdgesonRobustnessofCoupledNetworksAgainstCascadingFailures

选取合适的耦合网络模型和网络间的连接模式，能有效预防相继故障在耦合网络上大范围的传播扩散。综上所述，对于一个给定的BA无标度网络，在给定耦合网络模型(BA-BA或BA-ER)的条件下，最优耦合连接模式的顺序依次为AL>RL>DL，BA-BA(AL)是6种不同耦合网络中最稳健的耦合网络架构。

5.3 随机网络的对比分析

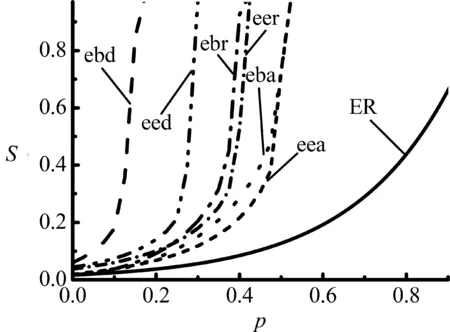
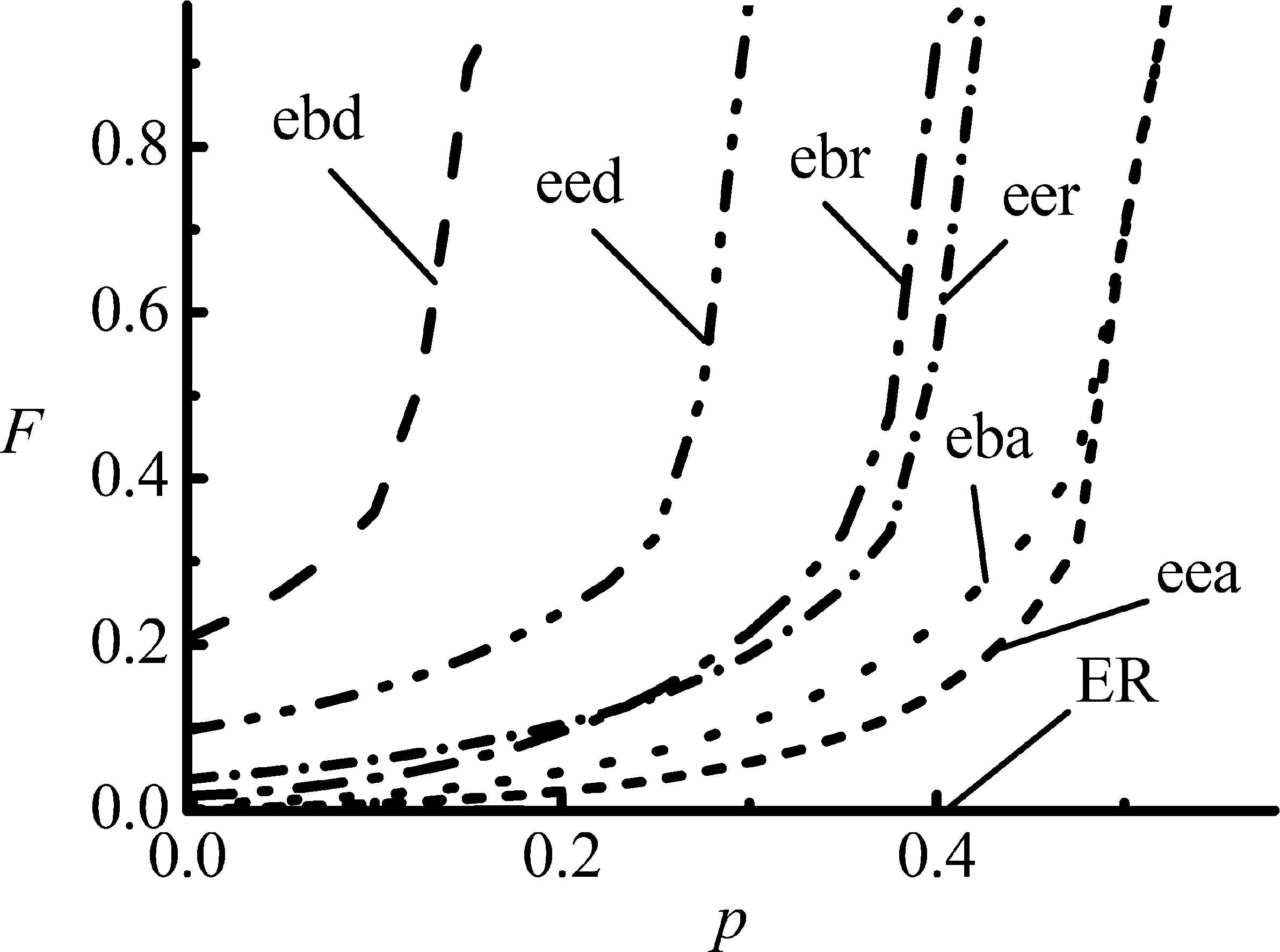
与基于无标度网络的研究方法类似，对于给定的ER随机网络，采用3种耦合连接模式，构建出6种两层次相互依赖的耦合网络模型，分别是ER-ER(RL)、ER-ER(AL)、ER-ER(DL)、ER-BA(RL)、ER-BA(AL)和ER-BA(DL)，两层次相互依赖的耦合网络模型在数值模拟图中简写为eer、eea、eed、ebr、eba和ebd；对比单层ER网络，所有网络的规模N=5 000，平均度〈k〉≈4。基于失效节点归一化S、失效点比例p(s)、失效边归一化F和P∞，图4给出不同连接模式下耦合网络模型与ER单层网络的鲁棒性的比较结果，图中每条曲线的模拟结果都是20个不同的耦合网络上相继故障数值模拟的平均结果。

(a) (b)

(c) (d)

图4不同连接模式下耦合网络模型与ER单层网络的对比
Figure4ComparisonbetweenCoupledNetworksandSingleERNetworkwithDifferentLinkPatterns

采用上一节中对相继故障的定量研究方法。图4(a)给出6种不同的耦合网络和ER单层网络关于失效节点归一化指标S和移除边的比例p之间的关系，从数值模拟的对比结果可以看出，耦合网络相比单层次网络在移除部分连边后更易导致相继故障的发生，并且边相继故障对耦合网络造成更严重的破坏性，依据度量指标的定义，可以看出ER-ER(AL)耦合网络架构比其他耦合网络模型表现出较强的抵制相继故障的鲁棒性。图4(b)给出6种不同的耦合网络和ER网络基于失效节点数量的差异p(s)与移除边的比例p之间的关系，综合关于失效节点的对比结果(图4(a)和图4(b))可看出，由ER网络组成的耦合网络中，最优的耦合网络架构的顺序依次为ER-ER(AL)>ER-BA(AL)>ER-ER(RL)>ER-BA(RL)>ER-ER(DL)>ER-BA(DL)。在基于失效边归一化指标F与参数p的数值模拟曲线中(图4(c))也能够得出上述相同的结果。在图4(d)中，对比几个网络在移除边比例为p的连边后导致的网络中相继故障的产生，相继故障经历了反复迭代的蔓延过程，直到最终的稳定状态时剩余网络的连通情况。对比在P∞指标模拟下不同耦合网络的渗流相变点pc的值，也可得出与上述3个指标数值模拟下相同的结论。数值模拟的结果能够对现实生活中基础设施的构建提供指导帮助。对于给定的基础设施网络，管理者可以选择最优的耦合连接模式抵制相继故障的大面积扩散，从而提高网络整体结构的鲁棒性。

对比在RL、AL和DL3种连接模式下的ER-ER和ER-BA耦合网络遭遇相继故障的结果，ER-ER(AL)耦合网络表现出更强的鲁棒性。ER-ER(AL)耦合网络在抵制相继故障中表现出的强鲁棒性主要源于以下3个方面。①ER随机网络节点度分布均匀，服从泊松分布，在网络中度远大于平均的度的节点几乎不存在，节点度之间差异性小；②对于模型中平均度相同的不同ER网络，同配连接(AL)模式又使同类型的2个网络耦合在一起时节点度之间更具相似性，即便在ER网络中可能存在孤立的节点或不连通的功能团，AL连接模式也会最大程度地弱化这种不确定性和结构的不完整性对耦合网络造成的破坏；③相似的网络结构以及相似的网络之间的耦合节点会使移除部分连边后相继故障蔓延的趋势趋于一致，产生的后果更相似，抑制了相继故障的进一步蔓延，很大程度上提高了网络的鲁棒性。然而，对于较异质的BA无标度网络而言，节点度之间存在很大的差异，网络中存在少量的度相对很大的节点，BA网络和ER网络两种截然不同的拓扑结构耦合在一起，移除部分边后相继故障在两层网络上蔓延的结果不同，将更易于导致耦合网络上连锁故障的大面积扩散。此外，同配耦合模式相比随机和异配两种连接模式更能减弱耦合网络之间节点度的差异性，使耦合网络表现出更强的相似性，在给定耦合网络模型(ER-ER或ER-BA)的条件下，最优的耦合连接模式顺序依然为AL>RL>DL。因此可以得出，在相同的网络规模和平均度下的耦合网络模型，耦合网络之间越相似，网络抵制相继故障的鲁棒性越强。

5.4 耦合网络的拓扑结构对鲁棒性的影响

在耦合网络中，基本网络拓扑模型的选择以及网络间耦合连接模式的差异都会影响网络抵制相继故障的鲁棒性大小。在上面的分析探讨中仅给定一层网络的拓扑结构，对比RL、AL和DL3种连接模式对耦合网络鲁棒性的影响，得出的结论是，对于给定的耦合网络结构，采用AL连接模式时网络整体表现出最强的鲁棒性。下面进一步探讨在确定耦合网络之间的连接模式下，网络模型的拓扑结构对鲁棒性的影响。网络的连通性能够很好地度量网络抵制相继故障的能力，因而选取P∞作为度量指标，研究在AL连接模式下，基于P∞与参数p之间的关系，探讨耦合网络的拓扑结构与鲁棒性之间的关联，结果如图5所示。

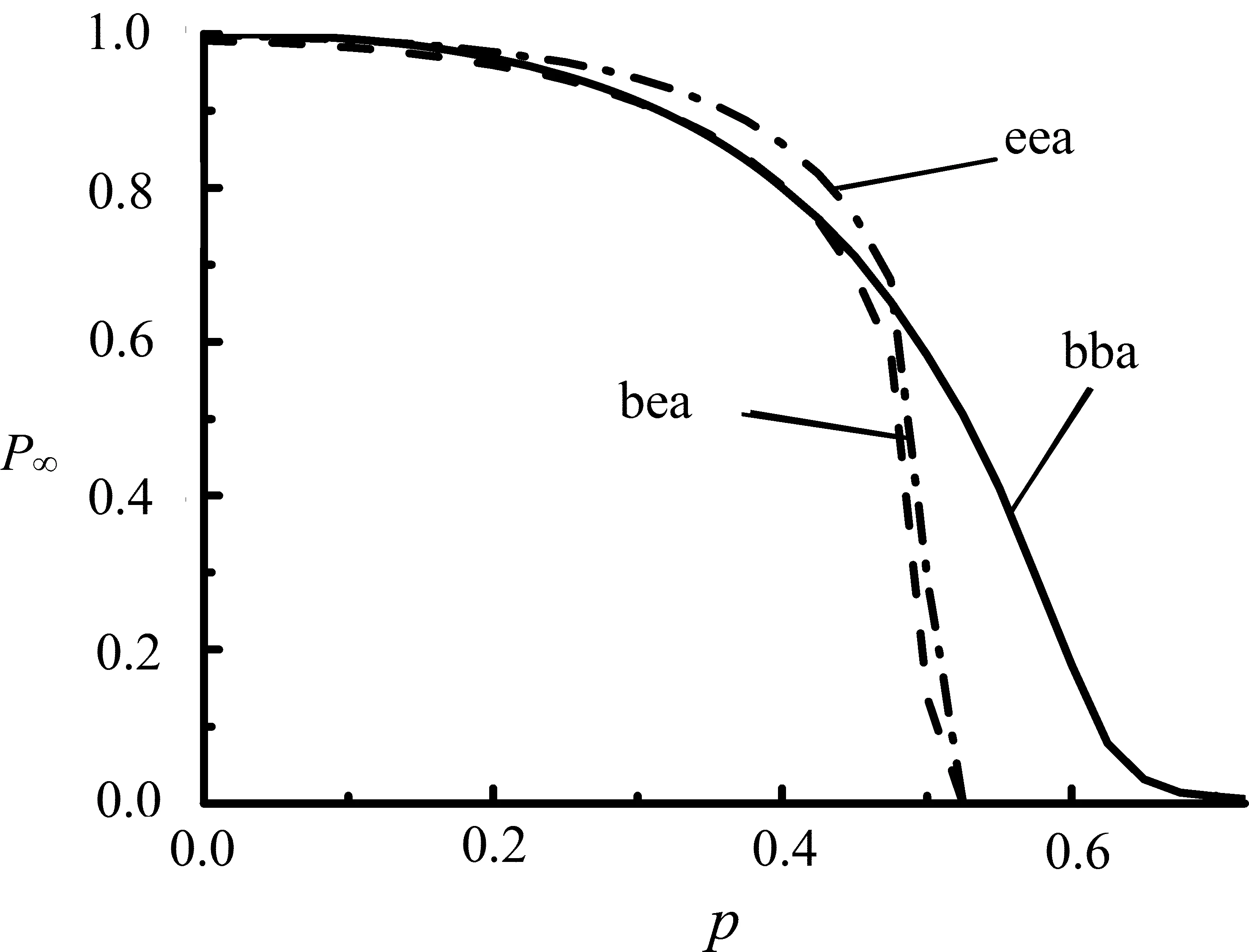
图5 AL连接模式对网络鲁棒性的影响Figure 5 Influence of AL Link Pattern on Network Robustness

由图5可知，在最优的AL耦合连接模式下，BA-BA和ER-ER耦合网络比BA-ER耦合网络表现出更强的抵制相继故障的鲁棒性。产生这种现象的原因在于，ER随机网络和BA无标度网络是两种度分布完全不同的复杂网络模型，ER随机网络是均匀网络，度分布服从泊松分布，网络中节点度的大小一般都分布在平均度的附近，远大于或远小于平均度的节点几乎不存在；而BA无标度网络的度分布具有幂律性质，网络的结构较异质。由于BA-ER耦合网络中两个网络在拓扑结构上表现出很大的差异性，相比于BA-BA和ER-ER具有相同拓扑结构的两个网络耦合在一起的耦合网络模型，将会使相继故障在BA-ER耦合的两层网络上演化的不对称性进一步导致连锁故障的发生。因此，在同配连接模式下，具有相同拓扑结构的网络组成的耦合网络模型具有更强的鲁棒性。

在1个网络中，平均度也是影响网络拓扑特性的1个重要指标，而在上述所有的数值模拟和探讨中，采用网络模型的平均度均为4。为了进一步研究网络拓扑结构与鲁棒性之间的关系，依然采用相同的网络规模N=5 000，在确定耦合连接模式的情况下，探讨BA-BA耦合网络平均度〈k〉与耦合网络连通性之间的关联，结果如图6所示。由于生成的ER网络可能会存在孤立的节点或不连通的功能团，为减少不确定性因素对实验模拟结果的影响，这里只考虑BA-BA耦合网络模型。

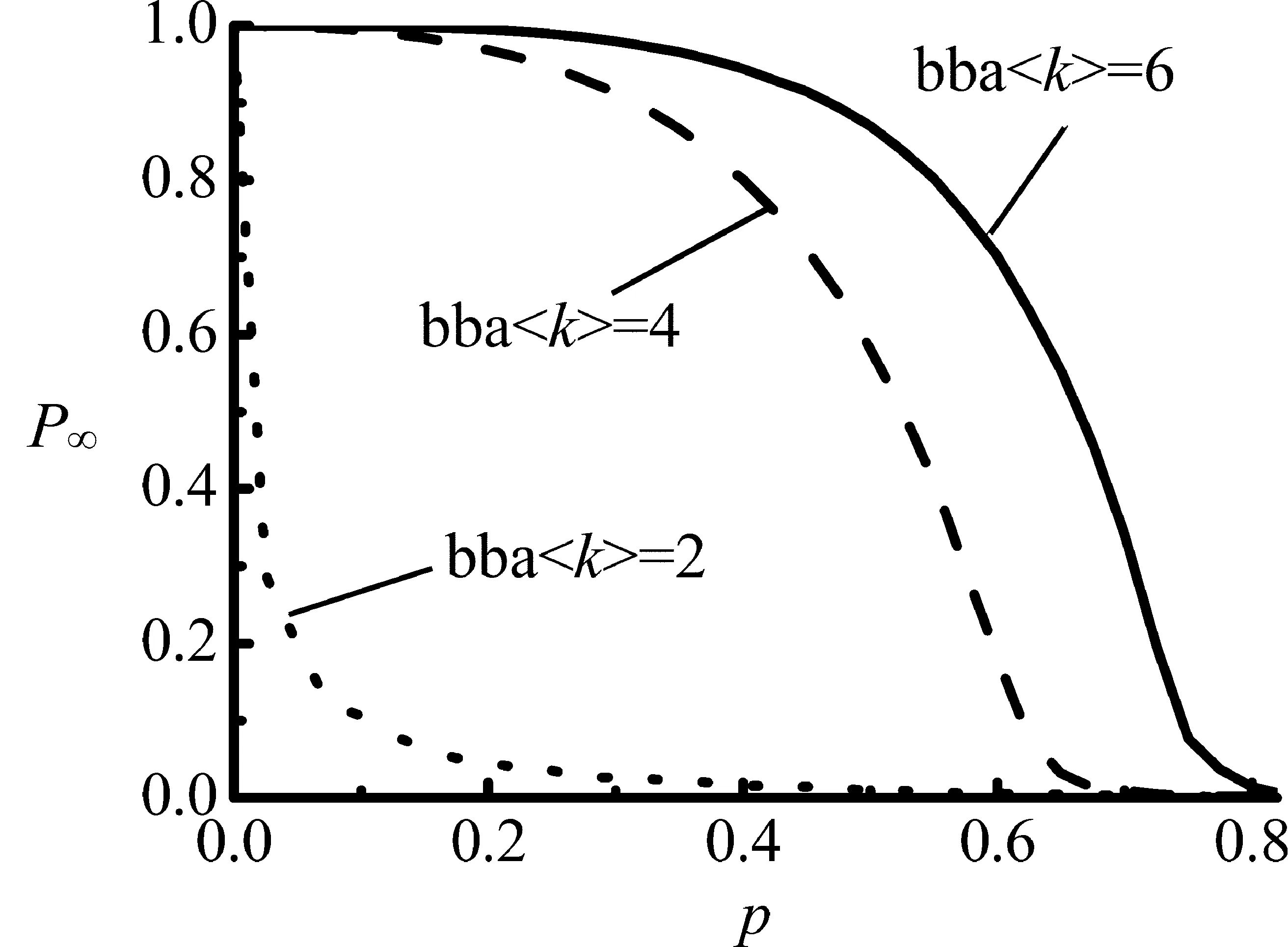
图6 AL耦合网络平均度对网络鲁棒性的影响Figure 6 Influence of Average Degree of Coupled Networks with AL on Network Robustness

在AL耦合连接模式下，对拥有不同平均度的BA-BA耦合网络进行数值模拟，采用度量指标P∞，通过相变点pc值衡量耦合网络抵制相继故障蔓延的鲁棒性强弱。从图6可以得出，相变点pc的值与网络平均度〈k〉呈正相关关系，即平均度〈k〉越大，pc值越大，耦合网络抵制相继故障的鲁棒性越强。平均度大的耦合网络表现出的强鲁棒性主要是由于连边数量的增多，使连接在一起的两个网络相互对称的连边数量增加，进而增加网络之间的相似度，减少了相继故障的进一步扩散。

进一步对比在RL和DL连接模式下平均度〈k〉对耦合网络鲁棒性的影响，结果如图7所示。从图7可以得出与AL连接模式下相同的结论，即平均度〈k〉越大，相变点pc值也越大，耦合网络抵制相继故障的鲁棒性越强。由于BA网络中节点度存在较大的异质性，AL连接模式可弱化耦合网络之间拓扑结构的差异，在平均度〈k〉及网络规模相同的情况下，3种连接模式的最优顺序依旧是AL>RL>DL。由于连边数量的增加导致网络之间拓扑结构的相似性，使网络表现出更强的抵制相继故障的鲁棒性。因此，提高网络结构的相似性可使网络的鲁棒性增强。

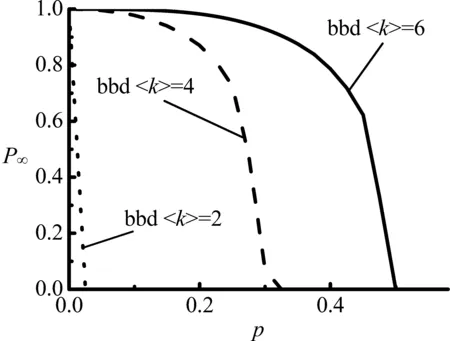
(a) (b)

图7RL和DL耦合网络平均度对网络鲁棒性的影响
Figure7InfluenceofAverageDegreeofCoupledNetworkswithRLandDLonNetworkRobustness

6 耦合网络边相继故障模型中的整体保护策略

相比单层次网络，在耦合网络上边的失效更易导致相继故障的爆发，边相继故障的蔓延对耦合网络也会造成更严重的破坏性。由于现实网络系统彼此间相互依赖，仅依靠单层次网络提出的保护策略不能很好的适用于耦合网络模型，因此需要建立基本的耦合网络模型模拟网络上的边相继故障现象，通过对不同的耦合网络模型的数值模拟分析，探讨对网络鲁棒性强弱的影响因素，进而提出有效抵制边相继故障蔓延的预防策略，构建稳健的耦合网络架构。由边相继故障的数值模拟结果可知，耦合网络之间的连接模式、网络基本模型的选择以及平均度等因素都对网络抵制相继故障的鲁棒性有影响。通过前面对模拟结果的分析，提出针对耦合网络上的整体保护策略，预防雪崩式的相继故障对网络造成的破坏。

(1)耦合连接模式。通过对3种不同连接模式的研究发现，对于确定的耦合网络模型，采用AL连接模式的耦合网络产生的对称连边数量最多，网络间相似性更大，边相继故障在两层次网络上的蔓延趋势更相似，进而表现出更强的抵制边相继故障的鲁棒性。因此，为了避免雪崩式的连锁故障对耦合网络造成大面积破坏，对于实际的耦合网络，如计算机-电网，在初建网络架构时应该尽量使耦合网络之间的连接模式服从同配连接。

(2)网络基本模型的选择。网络的拓扑结构是影响耦合网络鲁棒性的因素之一，数值模拟结果显示，在最优的AL连接模式下，具有相同拓扑结构的网络耦合在一起比不同拓扑结构组成的耦合网络表现出抵制相继故障蔓延的更强鲁棒性。不同的拓扑结构会使耦合在一起的网络节点度之间差异性大，相似性较差，相比之下也更脆弱。所以，为了避免拓扑结构的差异对耦合网络能力造成的影响，在现实生活中建设基础设施网络时，应尽量使耦合在一起的网络具有相似拓扑结构。

(3)网络的平均度。网络的平均度是指网络中每个节点平均的连边数，在一定程度上也可以认为是网络的投入成本，平均度越大，网络投入成本越高。如现实生活中的交通网络，平均度越大，平均通往每个路口的路线就越多，网络投入成本也就越多。依据数值模拟结果可以发现，在固定耦合网络架构时，网络的鲁棒性与平均度正相关，即平均度越大，网络鲁棒性越强。平均度的增大，使网络中连边数量增多，进而增加耦合网络间对称的连边数量，增加网络间的相似程度。考虑到现实情况中投入成本有限等客观因素，网络拓扑结构很难改变，可以适当地增加一些对称的连边，实现优化网络拓扑结构的目的。

7 实例分析

选择美国西部电力网络作为实例分析的对象[27]，美国西部电力网络的网络规模N=4 941，共6 594条边，平均度〈k〉≈2.670。对比美国电力网络与BA、ER两种拓扑结构网络基于3种不同的连接模式构成的两层次耦合网络拓扑模型在抵制边相继故障的鲁棒性方面的差异，目的是为建设最稳健的耦合网络架构，选择网络基本拓扑模型，在确定耦合网络模型的基础上匹配合适的连接模式。从耦合网络静态角度给出最优的耦合网络模型和网络间耦合模式，为指导现实网络系统的构建、保证基础设施网络安全稳定的运转提供参考性建议和指导。

电力网与ER、BA两个网络分别采用3种耦合模式，构建出6种不同结构的两层次耦合网络模型，分别是Power-BA(RL)、Power-BA(AL)、Power-BA(DL)、Power-ER(RL)、Power-ER(AL)和Power-ER(DL)，两层次相互依赖的耦合网络模型在数值模拟图中简写成pbr、pba、pbd、per、pea和ped，用Power代表电力网。在探讨耦合网络上的相继故障现象时，基于失效边归一化F、失效点归一化S和P∞度量指标，并对比单层Power网络，通过逐步增加移除边的比例p的方式，对比分析7种不同的网络抵制边相继故障的鲁棒性，每一个模拟结果都是20个不同的耦合网络上相继故障数值模拟的平均结果，数值模拟的结果如图8所示。

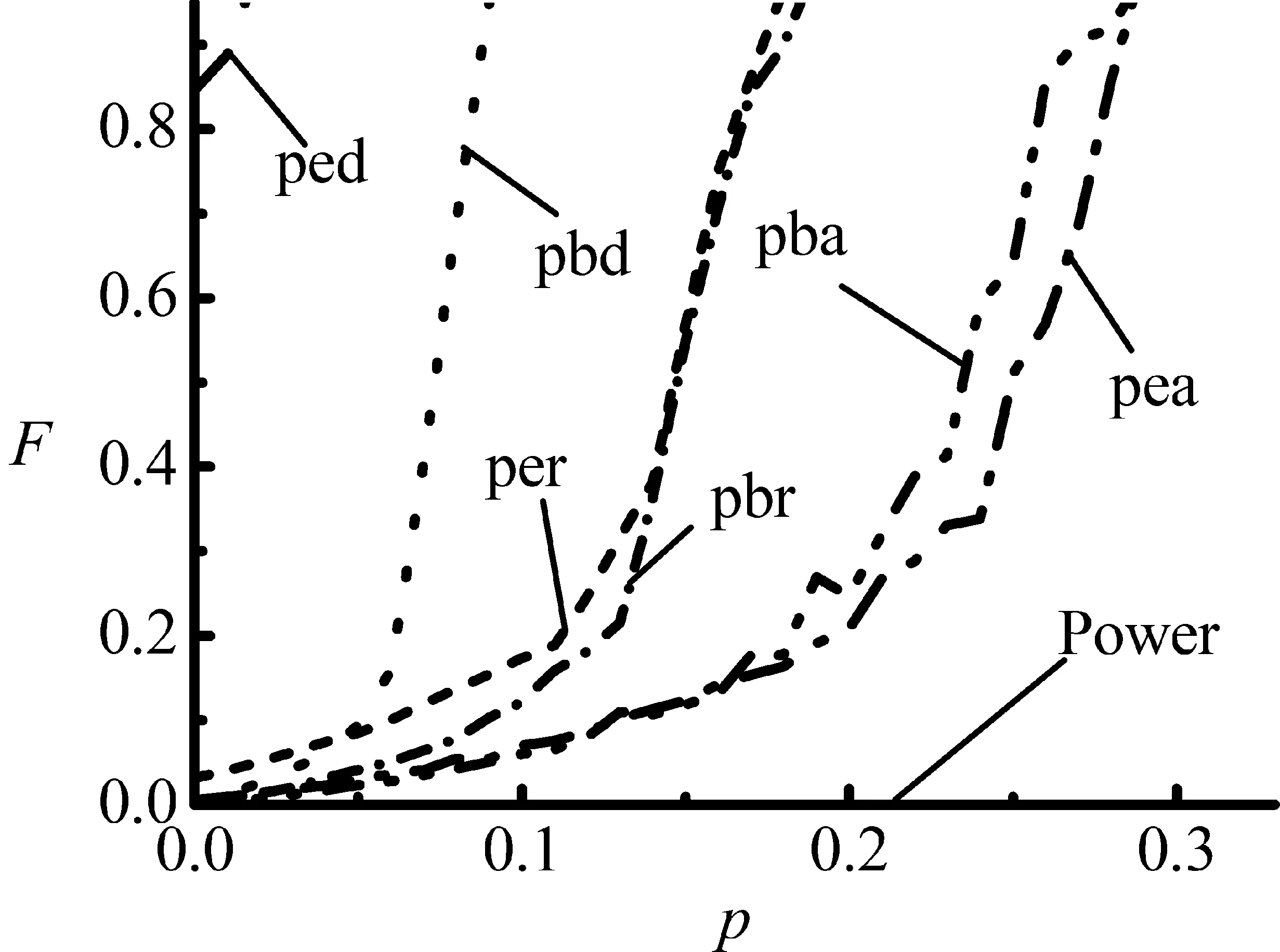
(a)

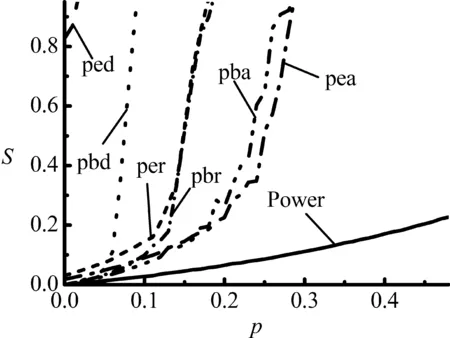
(b)

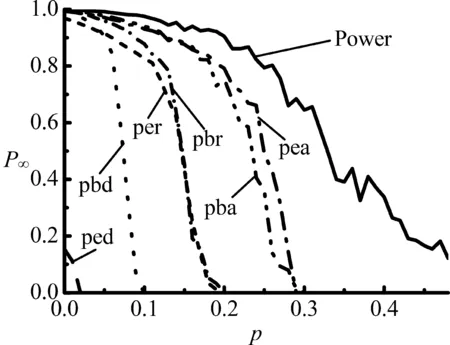
(c)

从图8能够明显的看出，无论是基于3个度量指标值，还是比较相变点p(c)值，电力网与BA网、ER网构成的耦合网络相比单层次电力网络更易引发大规模相继故障。由于耦合网络彼此耦合的特性，网络节点之间相互依赖，一层网络上的边发生故障，会使故障在两层网络上产生连锁反应。在不考虑网络负荷动态属性的情况下，单层网络上边的失效，不会继续引发网络上其他边的接连失效。因此，在边移除比例相同的情况下，耦合网络边的连锁故障对网络造成的破坏性更严重。对比6个不同拓扑结构的耦合网络模型基于3个度量指标模拟曲线得出的pc值可以看出，耦合网络间采用AL连接模式比采用DL和RL两种连接模式能更好地提高网络抵制相继故障的鲁棒性，按鲁棒性大小排列顺序依次为Power-ER(AL)>Power-BA(AL)>Power-BA(RL)>Power-ER(RL)>Power-BA(DL)>Power-ER(DL)。然而，采用AL连接模式的Power-ER、Power-BA两个耦合网络，在p值较小的情况下，基于3个度量指标可知，在p<0.070时，Power-BA耦合网络架构优于Power-ER网络，产生这种现象的原因在于，利用计算机生成网络规模为4 941、平均度约为4的ER网络可能会存在不完全连通、孤立点等不确定因素，ER网与电力网构成的耦合网络在边的移除比例p为0时，依据对耦合网络连通子团的定义，由于网络结构上彼此的不完全连通性，在没有人为移除任何边的情况下，依然可能会触发网络上的相继故障现象，这也能够很好地解释应用3种耦合连接模式的Power-ER耦合网络在p=0时失效边和失效点不归0、P∞不为1的原因。

基于上述的对比分析，从网络静态角度，为提高网络抵制故障蔓延的鲁棒性，对由电力网构成的耦合网络提出整体保护预防策略，即当给定网络基本模型时，AL连接模式下耦合网络的鲁棒性优于RL和DL两种连接模式；对比分析的所有耦合网络模型中，Power-ER(AL)耦合网络架构的鲁棒性最优，并且实际构建的ER网络系统能够有效避免生成ER网络时产生的一系列不确定性因素。基于此，研究结果为中国电网选择匹配的耦合网络、设计网络间的连接模式、优化网络结构的建设提供参考性依据，对构建具有稳定结构的耦合网络架构提供指导。

8 结论

本研究从耦合网络边的角度建立相继故障模型，重点研究由于边的失效导致的相继故障现象。通过仿真模拟和实例验证发现，与单层次网络相比，耦合网络更易导致大规模的相继故障的发生，并对网络整体造成更严重的破坏性后果。耦合网络间的连接模式、网络基本模型的选择、平均度等因素都关乎网络的能力，影响耦合网络鲁棒性大小的一个重要因素是网络中存在的对称连边，对称连边数量越多，相互耦合的网络之间拓扑结构越相似，网络抵制相继故障蔓延的鲁棒性越强。为了提高网络的鲁棒性，在现实网络建设时可以使同种类型的网络，应用同配耦合连接模式，并适当增加对称边数量，这样能够有效地提高网络的鲁棒性。应用本研究提出的整体保护策略，可以指导现实社会中基础设施耦合网络的构建，并为实际耦合网络上预防和控制雪崩式连锁故障对网络造成的破坏提供借鉴和参考依据。未来研究可在耦合网络静态属性的基础上进一步考虑负荷的动态变化，探讨负荷相继故障蔓延中的动力学过程。

[1]Chang L,Wu Z.Performance and reliability of electrical power grids under cascading failures[J].International Journal of Electrical Power & Energy Systems,2011,33(8):1410-1419.

[2]赵月.城市交通网络中相继故障问题的研究[J].交通信息与安全,2010,28(1):51-53,58.

Zhao Yue.Cascading failures on urban traffic networks[J].Journal of Transport Information and Safety,2010,28(1):51-53,58.(in Chinese)

[4]Motter A E,Lai Y C.Cascade-based attacks on complex networks[J].Physical Review E,2002,66(6):065102.

[5]Zhao L,Park K,Lai Y C.Attack vulnerability of scale-free networks due to cascading breakdown[J].Physical Review E,2004,70(3):035101.

[6]Zheng J F,Gao Z Y,Zhao X M.Modeling cascading failures in congested complex networks[J].Physica A:Statistical Mechanics and Its Applications,2007,385(2):700-706.

[7]任俊亮,申卯兴,仝蕊,高洪星.无尺度网络中降低相继故障规模的策略研究[J].计算机工程与应用,2011,47(33):82-84,161.

Ren Junliang,Shen Maoxing,Tong Rui,Gao Hongxing.Study of reducing size of cascading failures in scale-free network[J].Computer Engineering and Applications,2011,47(33):82-84,161.(in Chinese)

[8]Cao X B,Hong C,Du W B,Zhang J.Improving the network robustness against cascading failures by adding links[J].Chaos,Solitons & Fractals,2013,57:35-40.

[9]王皓.基于Web服务网络的相继故障模型[J].科技致富向导,2011(35):234-235.

Wang Hao.The cascading failure model based on Web service network[J].Guide of Sci-tech Magazine,2011(35):234-235.(in Chinese)

[10] 陈星光,周晶,朱振涛.基于耦合映像格子的城市交通系统相继故障研究[J].数学的实践与认识,2009,39(7):79-84.

Chen Xingguang,Zhou Jing,Zhu Zhentao.Cascading failures study of urban traffic system based on CML[J].Mathematics in Practice and Theory,2009,39(7):79-84.(in Chinese)

[11] 宋毅,王成山.具有时序特征的相继故障演变模型[J].中国电机工程学报,2008,28(22):29-34.

Song Yi,Wang Chengshan.A kind of continual fault evolution model with temporal characteristic[J].Proceedings of the CSEE,2008,28(22):29-34.(in Chinese)

[12] 朱凌峰,谭敏生.无标度网络上一种改进的基于节点有效路径的路由策略[J].电脑知识与技术,2010,6(31):8741-8743.

Zhu Lingfeng,Tan Minsheng.A improved routing strategy based on nodes′ efficient path on scale-free networks[J].Computer Knowledge and Technology,2010,6(31):8741-8743.(in Chinese)

[13] 段东立,战仁军.基于相继故障信息的网络节点重要度演化机理分析[J].物理学报,2014,63(6):068902-1-068902-9

Duan Dongli,Zhan Renjun.Evolution mechanism of node importance based on the information about cascading failures in complex networks[J].Acta Physica Sinica,2014,63(6):068902-1-068902-9.(in Chinese)

[14] Tessone C J,Garas A,Guerra B,Schweitzer F.How big is too big?Critical shocks for systemic failure cascades[J].Journal of Statistical Physics,2013,151(3/4):765-783.

[15] Holme P.Edge overload breakdown in evolving networks[J].Physical Review E,2002,66(3):036119.

[16] Wang W X,Chen G.Universal robustness characteristic of weighted networks against cascading failure[J].Physical Review E,2008,77(2):026101.

[17] Buldyrev S V,Parshani R,Paul G,Stanley H E,Havlin S.Catastrophic cascade of failures in interdependent networks[J].Nature,2010,464(7291):1025-1028.

[18] Parshani R,Buldyrev S V,Havlin S.Interdependent networks:Reducing the coupling strength leads to a change from a first to second order percolation transition[J].Physical Review Letters,2010,105(4):048701.

[19] Shao J,Buldyrev S V,Havlin S,Stanley H E.Cascade of failures in coupled network systems with multiple support-dependence relations[J].Physical Review E,2011,83(3):036166.

[20] Hu Y,Ksherim B,Cohen R,Havlin S.Percolation in interdependent and interconnected networks:Abrupt change from second- to first-order transitions[J].Physical Review E,2011,84(6):066116.

[21] Dong G,Gao J,Tian L,Du R,He Y.Percolation of partially interdependent networks under targeted attack[J].Physical Review E,2012,85(1):016112.

[22] 李稳国,邓曙光,崔治,李加升.相互依存网络边攻击下的相继故障研究[J].小型微型计算机系统,2013,34(3):576-579.

Li Wenguo,Deng Shuguang,Cui Zhi,Li Jiasheng.Cascade of failures in interdependent networks under attack of interdependent links[J].Journal of Chinese Computer Systems,2013,34(3):576-579.(in Chinese)

[23] Gao J,Buldyrev S V,Stanley H E,Xu X,Havlin S.Percolation of a general network of networks[J].Physical Review E,2013,88(6):062816.

[24] Dong G,Gao J,Du R,Tian L,Stanley H E,Havlin S.Robustness of network of networks under targeted attack[J].Physical Review E,2013,87(5):052804.

[26] Erdös P,Rényi A.On the evolution of random graphs[J].Publication of the Mathematical Institute of the Hungarian Academy of Sciences,1960,5:17-61.

[27] Watts D J,Strogatz S H.Collective dynamics of small-world′ networks[J].Nature,1998,393(6684):440-442.

StudyonCascadingFailures′ModelofEdgeinCoupledNetworks

Wang Jianwei，Jiang Chen，Sun Enhui

School of Business Administration, Northeastern University, Shenyang 110819, China

In order to deal with cascading failures in coupled networks, this study analyzes the dynamics mechanism of cascading failures and propose the cascading failures′ model of edge in coupled networks. To improve the robustness of coupled networks against cascading failures, according to different measures, this study takes multiple perspectives to analyze the correlation between the robustness of coupled networks with different link patterns and some parameters in our model. this study then discusses the influences of link patterns of coupled networks and the basic network model on cascading failures and states the whole protection strategies in the proposed model. This study finds: the assortative link pattern can enhance the robustness of coupled networks against cascading failures; the more similar the topological structures of two interdependent networks, the stronger the network robustness against cascading failures; the robustness of coupled networks has a positive correlation with the average degree; an appropriate increase in the number of symmetrical edges between two networks can improve the network robustness. Finally, the cascading failures′ model of edge in the real coupled power grid is analyzed.

cascading failures；coupled networks；link pattern；robustness

Date:June 5th, 2014

DateSeptember 15th, 2014

FundedProject:Supported by the National Natural Science Foundation of China(71101022) and the Program for New Century Excellent Talents in University(NCET-12-0100)

Biography:Dr.Wang Jianwei, a Liaoning Fuxin native(1978-), graduated from Dalian University and Technology and is an Associate Professor in the School of Business Administration at Northeastern University. His interests include emergency management and network science, etc.

E-mail：jwwang@mail.neu.edu.cn

N941.3

A

10.3969/j.issn.1672-0334.2014.06.012

1672-0334(2014)06-0132-11

2014-06-05修返日期2014-09-15

国家自然科学基金(71101022)；教育部新世纪优秀人才支持计划(NCET-12-0100)

王建伟(1978-)，男，辽宁阜新人，毕业于大连理工大学，获博士学位，现为东北大学工商管理学院副教授，研究方向：应急管理和网络科学等。E-mail：jwwang@mail.neu.edu.cn

□