考虑完成期限的电子商务在线订单分批模型及算法
王旭坪,张 珺,马 骏
1 大连理工大学 系统工程研究所,辽宁 大连 116023 2 大连理工大学 商学院,辽宁 盘锦 124221
考虑完成期限的电子商务在线订单分批模型及算法
王旭坪1,2,张 珺1,马 骏1
1 大连理工大学 系统工程研究所,辽宁 大连 116023 2 大连理工大学 商学院,辽宁 盘锦 124221
在电子商务在线订单拣选系统中,订单到达时间和订购商品等信息未知。针对拣选设备容量、员工人数等资源有限约束情况,研究在何时、对多少订单进行分批优化,以保证在订单完成期限前以最短的时间拣出最多的订单。构建考虑订单完成期限的在线订单分批混合整数规划模型,以最小化平均有效订单服务时间,采用改进的固定时间窗订单分批启发式规则求解模型,定义剩余操作时间在[前置时间,配送准备时间]内的订单为紧急订单,构建综合考虑紧急程度和相似度因素的在线订单分批算法。采用某配送中心14:00~18:00时间段内以泊松分布(λ=17)随机生成的订单进行数据实验,将实验结果与传统固定时间窗在线订单分批算法进行比较。研究结果表明,考虑完成期限时,系统拣选配送的订单数量更多,总服务时间和平均有效订单服务时间更短,且出现延迟订单的数量更少,延迟时间更短。拣选员工人数的增多在不同程度上提高配送率,且考虑完成期限时,配送率提高幅度要大于传统算法;但随着人数的增加,配送率的提高幅度呈降低趋势。
电子商务;在线订单拣选;订单分批;完成期限
1 引言
在人到货订单拣选系统中,订单分批是将1组订单集合分批为几个小的订单子集合,且每个批次由1名拣选员工进行拣选[1]。当订单中包含的商品足够多时,可由1名拣选员工完成1个订单,即按单拣选。但在电子商务环境下,订单具有小批量、高频次等特征,有必要采用订单分批策略减少总服务时间,提高拣选效率。且电子商务订单到达时间和订购商品等信息提前未知,管理人员不能等到订单全部到达后再拣选,而应进行实时的订单分批决策。同时顾客对商品到达时间更为敏感,为保证订单出库时间和顾客最终收货时间,配送中心会针对目的地的不同设置不同的配送车辆离开时间,即订单的完成期限。因此,有必要研究考虑完成期限的在线订单分批优化方法,将总服务时间和订单实际配送数量同时作为衡量系统运作效率的因素。本研究探讨电子商务环境下考虑完成期限的在线订单分批优化策略,拟解决的关键问题是,在配送时间确定的情况下,在何时、对多少订单、采用怎样的分批策略,以保证在配送车辆离开前以最短的服务时间配送出最多的订单,从出库环节优化电子商务物流配送系统。
2 相关研究评述
订单拣选是电子商务物流仓储作业的重要环节之一,是依据顾客订单信息准确迅速地将货物从存储位中拣出的过程[1]。传统的仓储操作中,订单拣选是最耗费时间和劳力的一项工作,成本约占总仓储费用的55%[2]。国内外学者对订单拣选效率优化方法的研究集中在货位设计[3-5]、拣选路径[6-9]、订单分批[10-11]和分区拣选[12-13]4种,但Petersen等[14]认为订单分批策略对拣选效率的提升更快。
订单分批优化最常见的优化目标是,在设备容量资源约束下最大化其拣选系统服务水平,服务水平的衡量指标包含订单服务时间、完成时间、延迟时间等。订单信息已知情况下进行的订单分批优化称为离线订单分批问题,由于订单分批问题为NP-hard问题,无法用精确算法求解[15],当前优化算法可大概分为5类。①优先规则算法[16],首先给顾客订单分配优先级,再根据优先级别对订单进行合并操作,并确保合并的批次不超过最大容量限制;②种子算法[13,17],包括种子订单选择阶段和订单合并阶段;③节约算法[18],计算两订单合并后行走距离比单独拣选的节约值,对节约从大到小进行排序,选取节约值最大的一对订单生成拣选批次;④启发式算法,如遗传算法[19]、蚁群算法[20]、贪婪算法[21]等;⑤数据挖掘方法,Chen等[22]介绍了一种新的订单合并方法,基于关联规则分析构建订单合并的整数规模模型,以最大化订单间的支持度;Hsieh等[23]基于数据挖掘中的K-均值聚类和自组织神经网络分类方法,构建了K-均值订单合并(KMB)和自组织神经网络订单合并(SOMB)两种新的订单合并规则。
但电子商务环境下,订单信息提前未知,企业需对到达的订单进行实时处理。此类订单分批问题又称为在线订单分批问题,所采用的分批策略可分为固定时间窗分批规则和可变时间窗分批规则。固定时间窗是将在某一固定时间范围内到达的订单进行合并生成拣选批次。Henn[20]和Bukchin等[24]分别从最小化总完成时间和最小化订单延迟时间的角度决定订单分批的开始时间。可变时间窗则是等待订单到达一定量后,将这些订单合并生成拣选批次。Chew等[25]、Le-Duc等[26]和Xu等[27]采用排队论等方法优化每一个批次需拣选订单数量。也有学者在订单分批优化时考虑完成期限约束。Tsai等[19]构建以行走距离成本和提前、延迟完成惩罚成本之和最小为目标的订单分批优化模型,并采用多阶段遗传算法求解;Henn等[28]将订单分批和分配排序问题进行联合优化,以最小化订单的总延迟时间,并构建局部迭代搜索和基于属性的爬山算法两种启发式方法求解模型;Azadnia等[29]考虑订单的完成期限,构建带权重的关联规则算法计算订单间的关联度,构建订单间关联度最大化的订单分批优化模型,采用求解旅行商问题的遗传算法求解合并批次的最优拣选路径,最后采用遗传算法对生成批次拣选顺序进行排序以最小化延迟时间;马士华等[30]将延迟制造思想引入到配送中心拣货作业中,提出基于时间延迟的动态时窗分批策略。总的来说,上述订单分批优化研究为后续的工作者提供了丰富的可借鉴策略,但多集中在订单信息已知下的离线订单分批策略[10-19],而少数在线分批优化仅假设拣选人员数量为1名[20,24-27],且未综合考虑拣选效率和配送效率对系统的影响[28-30]。因此,本研究在人员数量为多名的情况下,以总服务时间和订单实际配送数量作为优化目标,构建考虑完成期限的在线订单分批优化模型。面临如下决策问题,①合并拣选已经到达的订单还是继续等待更多的订单到达;②对已到达订单采用何种分批策略;③合并批次如何分配给有限的拣选员工。
本研究构建考虑订单完成期限的在线订单拣选分批优化模型,最小化平均有效订单服务时间;采用改进的固定时间窗订单分批启发式规则求解模型,即依据不同订单完成期限的紧急程度,构建紧急和非紧急情况下的两种不同分批算法;最后通过数据实验,从服务时间、完成订单数量、有效订单数量、延迟时间等多方面,将本研究算法与传统算法分批结果进行对比分析,以证明模型和算法的有效性,为仓储管理部门提高订单处理服务质量提供决策支持。
3 考虑完成期限的在线订单分批优化模型
3.1 问题描述和假设
图1为在线订单拣选系统示意图,分为订单分批系统和批次操作系统。
订单随机到达,进入订单分批系统,采用考虑完成期限的在线订单分批策略生成合并批次。批次进入操作系统,并按照先来先服务规则分配给空闲员工拣选;若无空闲员工,则排队等待。最后按单进行复核打包后,准备装车配送。系统中涉及到的时间如下。
到达时间,即订单进入订单分批系统时间;
进入时间,即订单合并生成拣选批次后进入操作系统的时间;
分批时间,即生成的拣选批次中最早订单到达时间与进入时间之差;
开始时间,即合并批次分配给空闲员工拣选的时间点;
等待时间,即合并批次进入操作系统等待服务的时间;
服务时间,即员工完成合并批次所需时间,包含拣货时的行走时间、拣取时间和准备时间等;
结束时间,即服务完成后的时间点;
剩余时间,若结束时间早于离开时间(完成期限),则两者差值为剩余时间;
延迟时间,若结束时间晚于离开时间(完成期限),则两者差值为延迟时间。
此拣选系统的特征可概括为,订单的完成期限由其所属目的地配送区域决定,即每个配送区域运输车辆的离开时间固定;订单陆续进入订单分批系统,订单到达信息提前未知;仓库雇佣员工完成拣选操作,且员工数量有限;员工只有完成当前批次任务后,才能进行下一个批次任务。要解决的关键问题是,如何合理进行订单分批和批次的分配,以最小化完成订单的总服务时间;在各配送区域车辆离开前拣出的最多订单数量,即有效订单最多。基于上述分析,模型的假设条件如下。①配送中心的拣选区域布局见图2,仓库类型为单区型,通道的入口在仓库的最左端,且每个通道的宽度相同;②订单信息提前未知;③拣选人员数量有限,允许出现订单合并批次排队等待;④采用遍历型的拣选路径策略,订单完成时间考虑行走时间、拣取时间和配送准备(复核、打包)时间;⑤由于各订单的配送期限不同,允许出现订单完成后配送车辆已经离开的情况;⑥配送车辆离开前某一段时间(设为准备时间)内到达的订单,直接列入第二天的拣选任务;⑦订单中至少包含一个商品,且在合并的过程中,需保证订单的完整性,即不得对订单进行分割;⑧每个商品的体积相同,每种商品只能存储在一个货架上,拣选员工行走在通道的中央同时从左右两边拣选商品;⑨生成的订单合并批次的容量不得超过拣选推车的容量上限;⑩拣选员工已知拣选任务单中的商品存储位置。
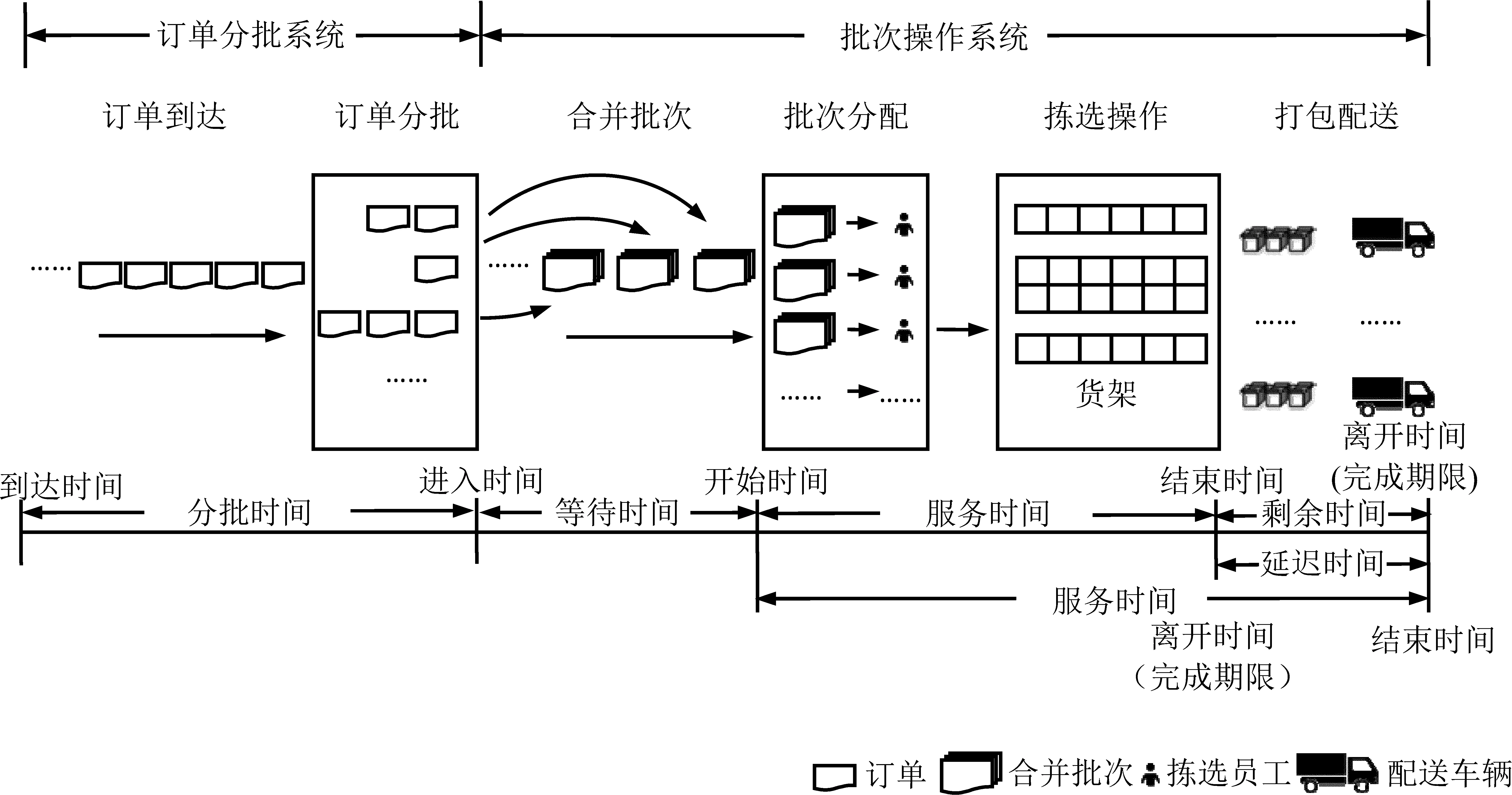
图1 在线订单拣选系统示意图Figure 1 Diagram of On-line Order Picking System
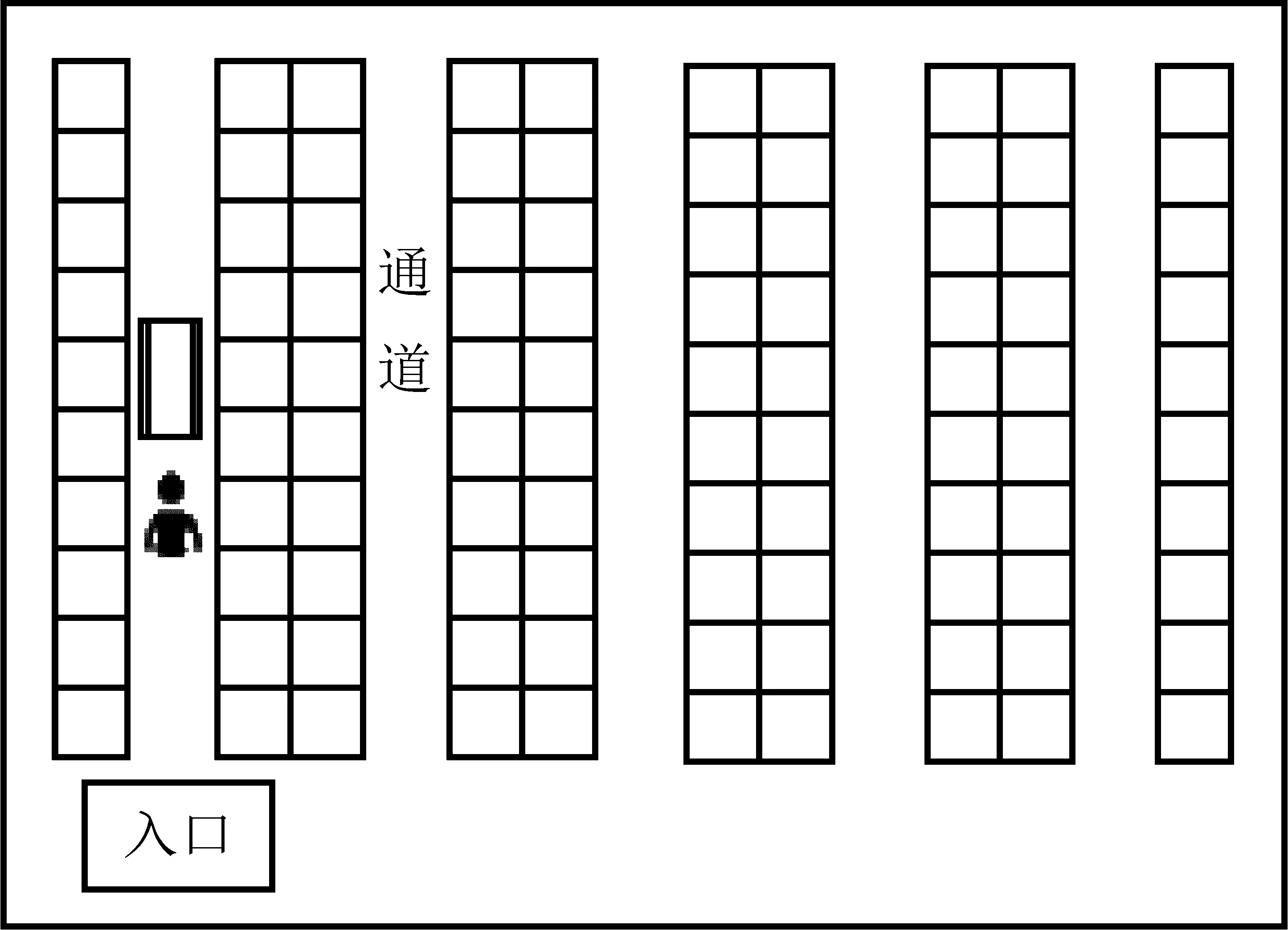
图2 拣选区域布局Figure 2 Layout of Picking Area
3.2 参数定义
本研究构建考虑完成期限的在线订单分批优化模型,首先对模型中的常量和变量作如下定义。
常量:
N为订单集合;
M为订单合并批次集合;
L为拣选人员集合;
O为配送目的地集合;
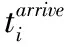
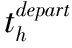
tpack为配送准备时间(复核、打包等所需时间);
qi为订单i中包含的商品数量;
Qb为每个合并批次能容纳的最大商品数量;
vtravel为单位时间拣选人员的行走距离;
vpick为单位时间拣选员工寻找并拣出商品数量;
zih为0-1变量,表示订单i是否属于目的地h,如果订单i属于目的地h,zih=1,否则zih=0;
变量:
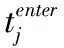
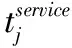
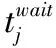
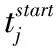
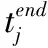
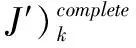
disj为完成批次j拣选任务所需行走距离(拣选路径优化策略采用遍历策略);
Tservice为完成订单的总服务时间;
R为有效订单数量,即拣选并装车配送出的订单数量;
xij为0-1变量,表示订单i是否分配给批次j,如果订单i分配给批次j,xij=1,否则xij=0;
yjk为0-1变量,表示批次j是否分配给拣选人员k,如果批次j分配给拣选人员k,yjk=1,否则yjk=0;
ri为0-1变量,表示订单i是否在配送车辆离开前完成,如果订单i在配送车辆离开前完成,ri=1,否则ri=0。
3.3 构建模型
基于上述分析,构建考虑完成期限的在线订单分批优化模型,以在有限的时间里完成更多的有效订单,提高拣选和配送效率。

(1)
(2)
(3)
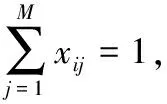
(4)
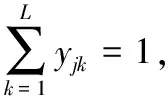
(5)
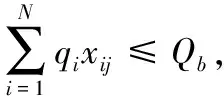
(6)
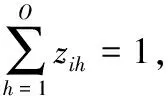
(7)
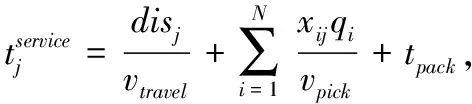
(8)
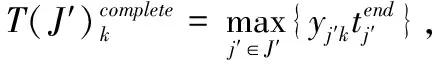
(9)
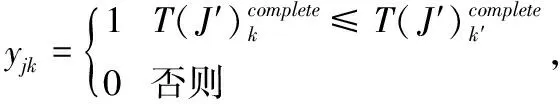
(10)
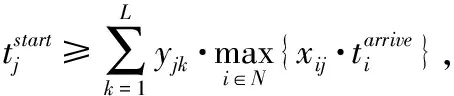
(11)
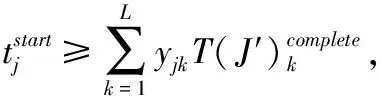
(12)
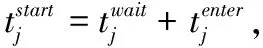
(13)
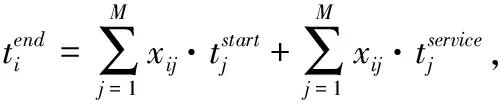
(14)
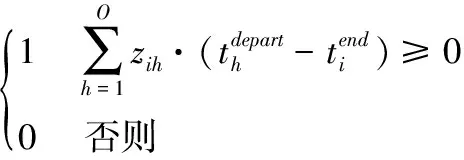
(15)
目标函数(1)式为最小化有效订单的平均服务时间;约束条件(2)式和(3)式分别为完成订单总服务时间和有效订单数量的表达式;约束条件(4)式~(7)式为对订单分批和配送目的地的限制,即保证一个订单只能分配给一个合并批次,一个合并批次只能分配给一个拣选人员,一个合并批次商品量不超过上限Qb,一个订单只能配送到一个目的地;约束条件(8)式定义批次j的服务时间,为行走时间、拣选时间和配送准备时间之和;约束条件(9)式和(10)式为对拣选人员分配批次的限制,即批次j仅分配给最早完成前期工作任务的拣选人员;约束条件(11)式~(13)式为对批次j开始服务时间的限制,即批次j应在其批次内的所有订单到达后开始,只有拣选完批次(j-1)才能开始下一个批次,批次j开始服务时间为该批次进入批次操作系统时间与等待时间之和;约束条件(14)式表明,订单i的结束时间为其所属批次j的开始时间与服务时间之和;约束条件(15)式表示,如果订单i在配送时间到达前完成,则ri=1,否则ri=0。
4 基于紧急程度的在线订单分批算法
4.1 整体算法设计思路
订单分批问题一直被认为是NP-hard问题,无法用精确算法求解[15]。本研究基于固定时间窗订单分批规则,综合考虑订单的紧急程度和相似度等因素,构建考虑订单紧急程度的固定时间窗订单分批启发式算法,实现对固定时间窗内到达订单的分批优化,以利用较短的时间在各配送目的地车辆离开前完成更多订单。
(1)定义订单i的紧急程度urgent为

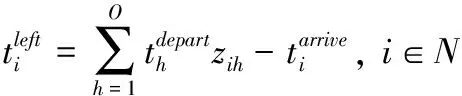
(16)
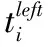
(2)定义订单间的相似度
本研究选取种子算法订单分批规则中的两两订单相同通道数系数simiii′作为衡量订单间相似度的指标,具体公式为
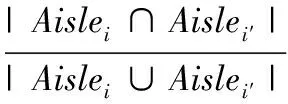
(17)
其中,Aislei为完成订单i需通过的通道数量,Aislei′为完成订单i′需通过的通道数量,|Aislei∩Aislei′|为订单i与订单i′间相同拣选通道数量;|Aislei∪Aislei′|为订单i与订单i′合并后总拣选通道数量。
算法整体思路见图3。
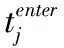
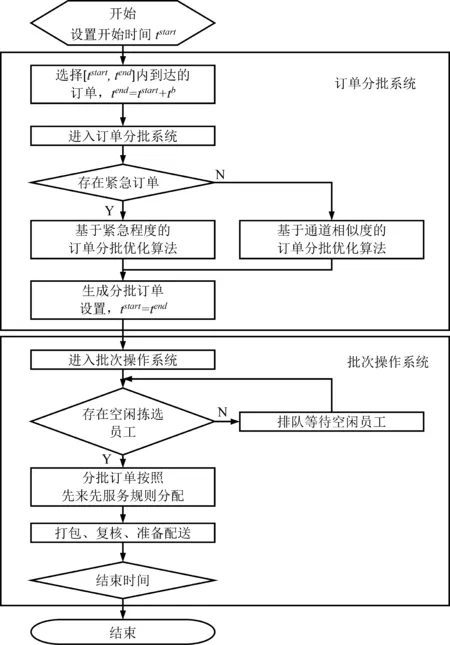
图3 算法流程图Figure 3 Flowchart of the Algorithm
4.2 基于通道相似度的订单分批优化算法
若时间窗内到达的订单不包含紧急订单,则采用基于通道相似度的订单分批优化算法。从全局的角度考虑订单间的相似性,每次进行订单合并时都选取订单集合中相似度最高的两个订单,合并后生成的新订单重新放回订单集合中,且在合并过程中需满足设备容量约束。设在时间窗内到达的订单集合为OS,具体分批步骤如下。
步骤1 计算相似度。若订单集合中包含不止1个订单,计算订单集合OS中各订单间相似度;否则运行步骤6。
步骤2 选择订单。选择相似度最大的订单Oi和Oj,容量分别为Qi和Qj。
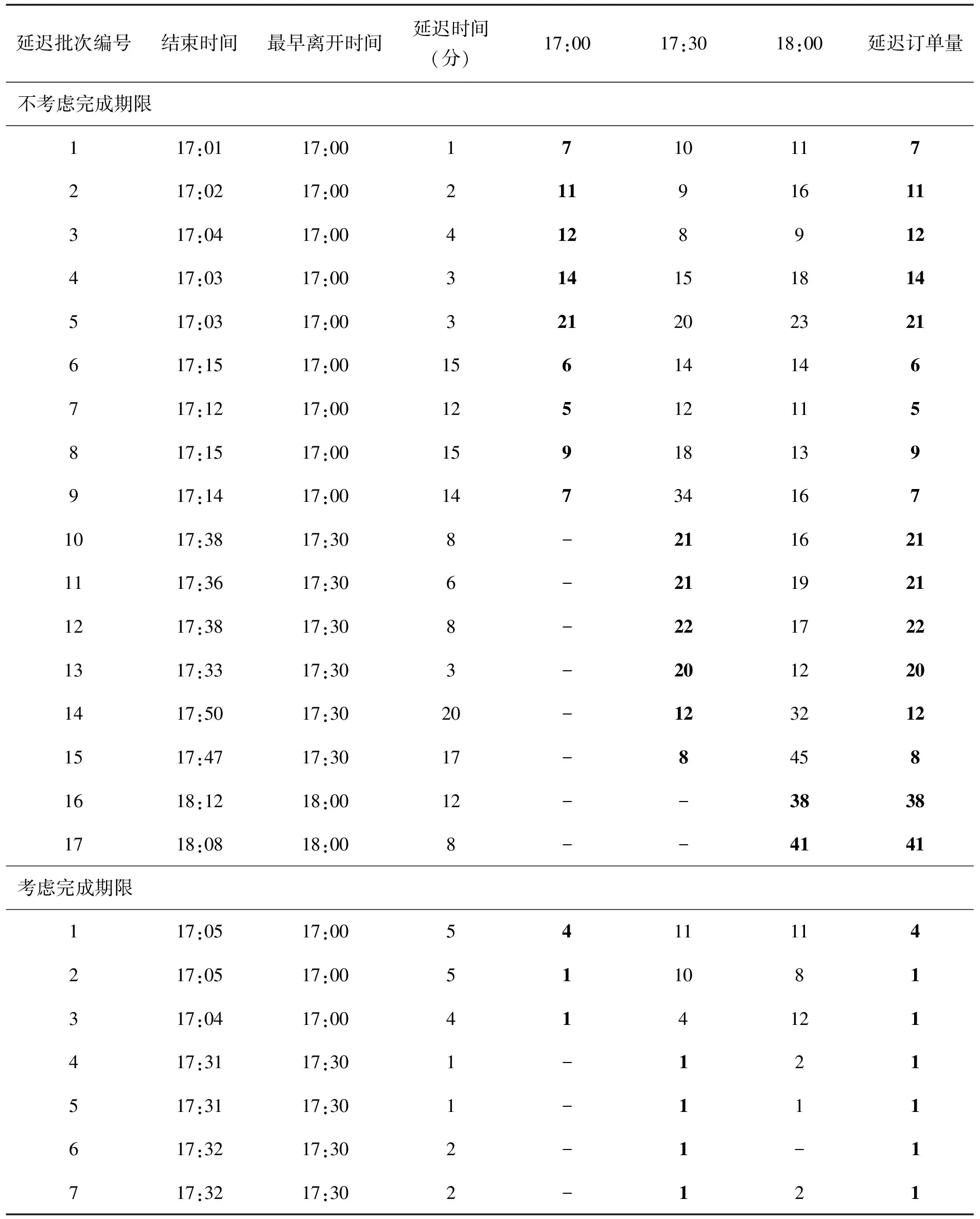
步骤3 订单合并。判断订单分批的容量约束,即
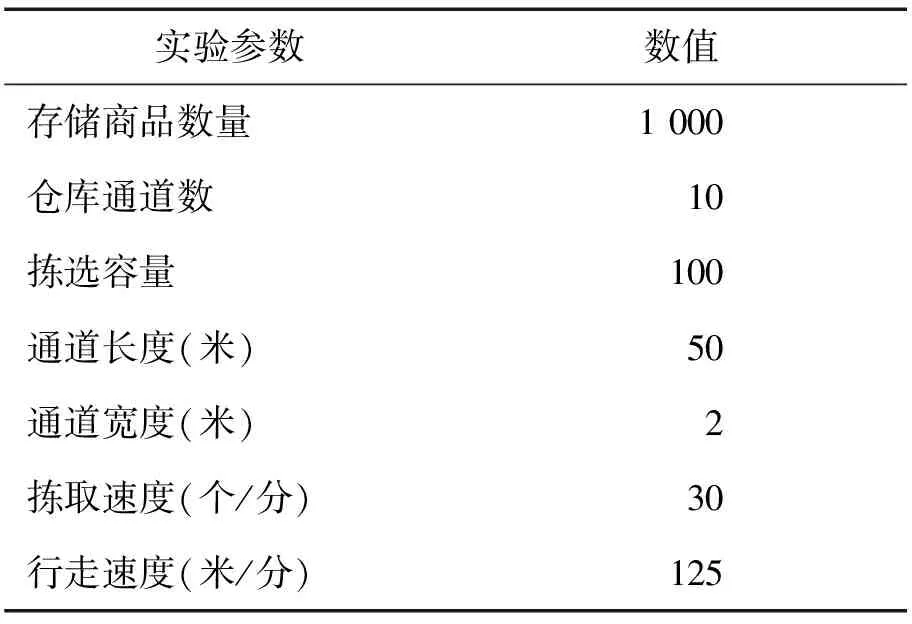
①若Qi+Qj ②若Qi+Qj=Qb,则满足容量约束,合并{Oi,Oj}后生成拣选批次,将Oi和Oj从订单集合删除,返回步骤1; ③若Qi+Qj>Qb,则不满足容量约束,继续运行。 步骤4 选择其他订单进行合并。选择Oi与Oj间容量较大的订单(如Oi),计算Oi与其他订单间的相似度。如果存在与Oi相似度较大的订单Om,满足容量约束Qi+Qm≤Qb,则合并{Oi,Om}后生成拣选批次,将Oi和Om从订单集合删除,返回步骤1;否则继续运行。 步骤5 直接生成拣选批次。如不存在满足容量约束的订单与Oi合并,则直接将Oi生成拣选批次,将Oi从订单集合中删除,返回步骤1。 步骤6 订单集合剩余1个订单,直接将其生成拣选批次。 步骤7 结束。 若时间窗内到达的订单包含紧急订单,采用基于紧急程度的订单分批优化算法。设在时间窗内到达的订单集合为OO,具体分批步骤如下。 步骤1 选取种子订单。若订单集合存在不止1个订单,选取紧急程度最高的订单为种子订单Oseed,容量为Qseed;否则运行步骤5。 步骤2 订单合并。计算种子订单Oseed与其他订单间的相似度,选取相似度最大的订单Oi,容量为Qi。设Oseed与Oi合并后的服务时间为service_time(Oseed,Oi),进入时间为enter_time(Oseed,Oi),若满足配送期限要求(分批时不考虑批次操作时可能的等待时间),则 service_time(Oseed,Oi)+enter_time(Oseed,Oi)≤ mindepart_time(Oseed,Oi) 判断订单分批的容量约束,即 ①若Qseed+Qi ②若Qseed+Qi=Qb,则满足容量约束,合并{Oseed,Oi}生成拣选批次,将Oseed和Oi从订单集合中删除,返回步骤1。 ③若Qseed+Qi>Qb,则不满足容量约束,继续运行。 步骤3 不满足配送期限要求,选择其他订单生成拣选批次。选择订单集合中与Oseed相似度较大的订单Oi′。若同时满足配送期限约束和容量约束,合并{Oseed,Oi′}生成拣选批次,将Oseed和Oi′从订单集合中删除,返回步骤1;否则继续运行。 步骤4 直接生成拣选批次。若不存在满足配送期限约束或容量约束的订单与Oseed合并,则直接将Oseed生成拣选批次,将Oseed从订单集合中删除,返回步骤1。 步骤5 订单集合OO剩余1个订单,直接将其生成拣选批次。 步骤6 结束。 将传统基于固定时间窗的种子算法[16]与本研究提出的算法进行比较,主要区别体现在仅以订单拣选效率作为优化目标,未考虑订单的紧急程度。种子算法主要分为种子订单选择阶段和合并订单选择阶段,当前有关种子订单的选择规则和订单合并的规则有很多,本研究采用(17)式相同通道系数作为订单间相似度的度量方式,而种子订单的选择规则采用随机规则。生成的拣选批次同样采用先来先服务规则分配给空闲拣选员工,并最终打包配送到顾客手中。订单分批具体步骤如下。 步骤1 收集到达订单。开始时间为tstart,设在[tstart,tend](tend=tstart+tb)内到达的订单集合为O′。 步骤5 更新时间窗。更新tstart=tend,返回步骤1;如到达系统结束时间,运行步骤6。 步骤6 结束。 目前对电子商务在线订单分批问题尚未有标准的验证数据,且不同商家订单量差异较大,难以采用统一的数据衡量。为验证模型和算法的有效性,本研究尽量贴近实际,订单到达情况服从泊松分布;考虑电商订单小批量、高频次且多数商家日交易量可达万单等特征,假设平均每分钟到达订单数量为17,满足泊松分布,即λ=17,每单包含商品数量服从[1,3]的随机分布;由于车辆离开时间常为17:00~18:00,按照λ=17的泊松分布随机产生14:00~18:00时间段内到达的订单,图4给出对随机生成订单在不同时段数量的统计。拣选区域参数见表1,其中包含10个拣选通道和1 000种商品,每列货架存放50种商品,每个员工一次拣选的最大商品容量为100个。假设每个商品的体积相同,且只能存储在一个货架上;拣选员工行走在通道的中央,以便同时从左右两边拣选商品;员工通常从最左边的入口进入,拣取完所有商品后回到入口处。 表1 拣选区域参数Table 1 Parameters of the Picking Area 算法参数设置如下。分批时间窗大小tb为10分钟;订单标记为紧急订单的前置时间tadv为60分钟;配送准备时间tpack为10分钟;存在3个不同的配送区域,订单所属配送区域满足随机分布;各配送区域运输车辆的离开时间分别是17:00、17:30和18:00。 图4 各时段订单到达数量统计Figure 4 Summary of the Number of Arrival Orders in Each Time Interval 本部分将考虑完成期限与不考虑完成期限两种情况下所得分批结果进行对比分析。不考虑完成期限时直接采取基于通道相似度的订单分批算法,以最小化平均完成订单服务时间为目标。当进入订单分批系统生成合并批次后,可得批次数量、完成订单量、总服务时间等。两种情况下合并批次实验结果见表2,合并批次数量分别为94和86,完成订单量为3 363和3 589。考虑配送期限时,生成的批次数量大于不考虑配送期限的情况。主要原因是,为了保证紧急程度较高的订单在运输车辆离开前拣选完成,系统会根据配送期限约束,单独将紧急订单生成拣选批次或只选取少量订单与其合并,从而造成合并批次数量较多。而考虑完成期限时,完成订单数量略少于不考虑配送期限的情况,考虑完成期限的订单完成率为80.822%,不考虑完成期限的完成率为86.253%。原因在于,基于紧急程度的订单分批优化算法将剩余操作时间小于配送准备时间的订单直接列入第2天的拣选任务,使实际进行操作的订单量减小。拣选完这些合并批次所需总服务时间分别为614分钟和643分钟,说明考虑完成期限时,完成生成的合并任务所需耗费的服务时间更少,效率更高。 表2 两种情况下合并批次实验结果Table 2 Merged Batching Results of Two Situations 当生成的合并批次进入批次操作系统,将拣选批次分配给拣选员工完成后,即可得到有效订单量、平均有效订单服务时间、延迟时间等。由于拣选员工数量会影响等待时间、有效订单数量等,本实验设配送中心的拣选员工分别为2人~6人,分析不同雇佣情况下的实验结果。基于不同拣选员工数量的批次操作实验结果见表3,两种不同的分批情况下几个评价指标变化趋势基本一致,随着员工数量的增加,进入系统的合并批次所需等待时间减少,相应的平均有效订单服务时间、延迟时间随之减少,有效订单量和剩余时间随之增加。增加拣选员工人数能不同程度增加订单拣选效率,当员工数从2人增至3人时,等待时间减少80%以上,延迟时间减少90%以上,但雇佣成本会随之增加。另外,通过配送率可以看出,当员工数从2人增加到4人时,两种不同情况下的配送率提高幅度分别为26.532%和26.772%;但当员工从4人增加到6人时,提高幅度只有0.269%和0,此时为提高配送率而增加雇佣成本意义不大。 通过对两种分批结果比较可以看出,当拣选员工从2人逐渐增加到6人时,考虑完成期限拣出的有效订单数量分别是2 240、3 048、3 344、3 347、3 353,相较不考虑完成期限时分别增加40、70、30、33、39;而两种不同分批策略下的总服务时间分别为641分钟和643分钟,说明考虑完成期限的订单分批策略能在更短的服务时间里拣选并配送出更多的订单。同时在不同的雇佣情况下,考虑完成期限情况下的剩余时间要大于不考虑完成期限,使员工有更宽裕的配送准备时间。从表3可以看出,本研究构建的模型和算法很大程度上减少了订单延迟时间,当雇佣人数为6人时,延迟时间减少比例高达98.404%。另外,由于生成批次数量多而每个批次包含的平均订单量少,考虑配送期限时的排队等待时间略大。 延迟时间一般作为评价订单拣选系统效率的一个常用指标[25-30],本部分对拣选员工人数为6人时存在延迟订单的合并批次进行分析。员工为6人时的延迟订单信息见表4,17:00、17:30和18:00三列分别表示此配送期限的订单数量;延迟时间为该批次结束时间与最早离开时间之差,黑体数字为存在延迟的订单数量。在不考虑配送期限的情况下,有17组合并批次存在延迟,总延迟订单数量为275个,总延迟时间为2 255分钟。考虑配送期限的情况下,有7组合并批次存在延迟情况,延迟订单总量为10个,降低96.364%;总延迟时间为35分钟,降低98.448%。可以看出本研究构建的模型和算法能有效地减少延迟订单数量和延迟时间。 表3 基于不同拣选员工数量的两种情况下批次操作实验结果Table 3 Batching Operation Results of Two Situations under Different Number of Pickers 综上所述,可得出如下结论。 (1)考虑配送期限时,完成的订单数量小于不考虑配送期限的情况,且总服务时间小于不考虑配送期限的情况; (2)考虑配送期限时,拣选出的有效订单数量更多,平均有效订单服务时间更短; (3)考虑配送期限时,出现延迟订单的数量更少,延迟时间更短; (4)随着雇佣拣选人员数量的增多,批次操作系统拣出的有效订单量增大,合并批次排队等待拣选的时间减少,完成订单延迟时间减少,但雇佣成本增加; (5)当拣选人员为4人时,考虑完成期限情况下订单配送率为80.365%,为该数据实验的最优员工数量。 实验结果验证了模型和算法的有效性,考虑完成期限的订单分批优化策略有利于在运输车辆离开前以更短的时间拣出更多的订单,从出库环节提升了电子商务物流配送速度。 针对电子商务环境下订单实时到达的情况,平衡订单开始拣选时间和拣选量的关系,同时综合考虑订单离开时间,从配送中心运作环节提高电子商务物流配送效率。通过构建考虑完成期限的在线订单分批优化模型,并采用基于订单紧急程度的固定时间窗订单分批启发式算法,实现对固定时间窗内到达订单的分批优化。 研究结果表明,在制定分批规则时考虑订单完成期限,有利于缩短完成时间和延迟时间,增加有效订单量,在运输车辆离开前以更短的时间拣出更多的订单;同时雇佣人数的增多在不同程度上提高了配送率,但随着人数的增加配送提高率呈降低趋势,因此在雇佣员工时需综合考虑雇佣成本和配送率间的关系。值得一提的是,固定时间窗的订单分批规则更适用于订单到达数量波动较小的情况,在波动较大的情况下,需综合考虑订单到达数量和时间的关系,采用时间-量混合的订单分批规则求解模型,这样保证了在不同的订单到达情况下可以采用本研究的模型和算法。 综上所述,本研究从仓储配送中心存在的实际操作问题出发,综合考虑配送车辆离开期限和订单分批合并效率,有助于加深对订单拣选系统的理解,对改进订单分批优化策略具有理论分析价值和实践指导意义,为仓储管理部门提高订单处理速度提供决策支持。本研究采用固定时间窗分批规则,未考虑订单的波动性对拣选效率的影响,更复杂的在线分批规则可能同时考虑固定时间窗和固定订单量的混合分批规则。另外,随着顾客对订单到达时间要求的提升,可从在线订单拣选和配送调度整合优化方面开展进一步的研究。 表4 拣选员工人数为6人时的延迟订单信息Table 4 Delayed Orders′ Information with Six Pickers 注:不考虑完成期限的情况下,总延迟时间=延迟批次1的延迟时间×延迟订单量+延迟批次2的延迟时间×延迟订单量+…+延迟批次17的延迟时间×延迟订单量=2 255分;考虑完成期的情况下,总延迟时间=延迟批次1的延迟时间×延迟订单量+延迟批次2的延迟时间×延迟订单量+…+延迟批次7的延迟时间×延迟订单量=35分。 [1]de Koster R,Le-Duc T,Roodbergen K J.Design and control of warehouse order picking:A literature review[J].European Journal of Operational Research,2007,182(2):481-501. [2]Manzini R.Warehousing in the global supply chain:Advanced models,tools and applications for storage[M].Berlin:Spinger,2012:1-30. [3]Xiao J,Zheng L.Correlated storage assignment to minimize zone visits for BOM picking[J].The International Journal of Advanced Manufacturing Technology,2012,61(5/8):797-807. [4]朱杰,周丽,郭键.分类存储人工拣选随机服务系统效率研究[J].管理科学学报,2012,15(2):59-71. Zhu Jie,Zhou Li,Guo Jian.Research on random service system efficiency of sorted storage manual order picking manners[J].Journal of Management Sciences in China,2012,15(2):59-71.(in Chinese) [5]邓爱民,蔡佳,毛浪.基于时间的自动化立体仓库货位优化模型研究[J].中国管理科学,2013,21(6):107-112. Deng Aimin,Cai Jia,Mao Lang.Research on slotting optimization in automated warehouse based on time[J].Chinese Journal of Management Science,2013,21(6):107-112.(in Chinese) [6]陈方宇,王红卫,祁超,谢勇.考虑多拣货员堵塞的仓库拣选路径算法[J].系统工程学报,2013,28(5):581-591. Chen Fangyu,Wang Hongwei,Qi Chao,Xie Yong.Routing method for multiple order pickers with congestion consideration[J].Journal of Systems Engineering,2013,28(5):581-591.(in Chinese) [7]朱杰,郭键,周丽.随机存储下返回型与S型拣选路径随机模型的比较研究[J].系统仿真学报,2011,23(2):223-227. Zhu Jie,Guo Jian,Zhou Li.Comparative research on stochastic model of random-storage return-type and S-type order picking route[J].Journal of System Simulation,2011,23(2):223-227.(in Chinese) [8]陈璐,陆志强.自动化立体仓库中的储位分配及存取路径优化[J].管理工程学报,2012,26(1):42-47. Chen Lu,Lu Zhiqiang.Optimization for storage location assignments and interleaving problems in an automated storage/retrieval system[J].Journal of Industrial Engineering and Engineering Management,2012,26(1):42-47.(in Chinese) [9]胡少龙,胡志华,曹杨.基于多候选储位的存取路径优化问题研究[J].运筹与管理,2013,22(5):111-116,165. Hu Shaolong,Hu Zhihua,Cao Yang.Optimization for storage or retrieval routing problem based on mutil-candidates storages location[J].Operations Research and Management Science,2013,22(5):111-116,165.(in Chinese) [10] Hong S,Johnson A L,Peters B A.Large-scale order batching in parallel-aisle picking systems[J].IIE Transactions,2012,44(2):88-106. [11] 李诗珍,杜文宏.基于聚类分析的订单分批拣货模型及启发式算法[J].统计与决策,2008(12):53-56. Li Shizhen,Du Wenhong.Order batching model and algorithm based on similarity analysis[J].Statistics & Decision,2008(12):53-56.(in Chinese) [12] 吴颖颖,吴耀华.基于并行拣选的自动拣选系统订单拆分优化[J].计算机集成制造系统,2012,18(10):2264-2272. Wu Yingying,Wu Yaohua.Order splitting for automated picking system based on parallel picking strategy[J].Computer Integrated Manufacturing Systems,2012,18(10):2264-2272.(in Chinese) [13] 李诗珍.基于工作量均衡的分区同步拣货系统储位分配与评价[J].包装工程,2010,31(11):114-118. Li Shizhen.Location assignment and evaluation in a synchronized zone picking system base on workload balance[J].Packaging Engineering,2010,31(11):114-118.(in Chinese) [14] Petersen C G,Aase G.A comparison of picking,storage,and routing policies in manual order picking[J].International Journal of Production Economics,2004,92(1):11-19. [15] Gademann N,van de Velde S.Order batching to minimize total travel time in a parallel-aisle warehouse[J].IIE Transactions,2005,37(1):63-75. [16] Lam C H Y,Choy K L,Ho G T S,Lee C K M.An order-picking operations system for managing the batching activities in a warehouse[J].International Journal of Systems Science,2014,45(6):1283-1295. [17] Ho Y C,Tseng Y Y.A study on order-batching methods of order-picking in a distribution centre with two cross-aisles[J].International Journal of Production Research,2006,44(17):3391-3417. [18] Bozer Y A,Kile J W.Order batching in walk-and-pick order picking systems[J].International Journal of Production Research,2008,46(7):1887-1909. [19] Tsai C Y,Liou J J H,Huang T M.Using a multiple-GA method to solve the batch picking problem:Considering travel distance and order due time[J].International Journal of Production Research,2008,46(22):6533-6555. [20] Henn S.Algorithms for on-line order batching in an order picking warehouse[J].Computers & Operations Research,2012,39(11):2549-2563. [21] Henn S,Wäscher G.Tabu search heuristics for the order batching problem in manual order picking systems[J].European Journal of Operational Research,2012,222(3):484-494. [22] Chen M C,Wu H P.An association-based clustering approach to order batching considering customer demand patterns[J].Omega:International Journal of Management Science,2005,33(4):333-343. [23] Hsieh L F,Huang Y C.New batch construction heuristics to optimise the performance of order picking systems[J].International Journal of Production Economics,2011,131(2):618-630. [24] Bukchin Y,Khmelnitsky E,Yakuel P.Optimizing a dynamic order-picking process[J].European Journal of Operational Research,2012,219(2):335-346. [25] Chew E P,Tang L C.Travel time analysis for general item location assignment in a rectangular warehouse[J].European Journal of Operational Research,1999,112(3):582-597. [26] Le-Duc T,de Koster R M B M.Travel time estimation and order batching in a 2-block warehouse[J].European Journal of Operational Research,2007,176(1):374-388. [27] Xu X,Liu T,Li K,Dong W.Evaluating order throughput time with variable time window batching[J].International Journal of Production Research,2014,52(8):2232-2242. [28] Henn S,Schmid V.Metaheuristics for order batching and sequencing in manual order picking systems[J].Computers & Industrial Engineering,2013,66(2):338-351. [29] Azadnia A H,Taheri S,Ghadimi P,Saman M Z M,Wong K Y.Order batching in warehouses by minimizing total tardiness:A hybrid approach of weighted association rule mining and genetic algorithms[J].The Scientific World Journal,2013:246578. [30] 马士华,文坚.基于时间延迟的订单分批策略研究[J].工业工程与管理,2004,9(6):1-4. Ma Shihua,Wen Jian.The order batching strategies based on time postponement[J].Industrial Engineering and Management,2004,9(6):1-4.(in Chinese) E-CommerceOn-lineOrderBatchingModelandAlgorithm:ConsideringDueTime Wang Xuping1,2,Zhang Jun1,Ma Jun1 1 Institute of Systems Engineering, Dalian University of Technology, Dalian 116023, China 2 School of Business, Dalian University of Technology, Panjin 124221, China In the e-commerce on-line order picking system, customer orders′ arrival time and goods cannot be informed in advance. With the constraints of picking equipment capacity and pickers′ number, the order batching optimization approach, which focuses on the batching time and batching strategy, is proposed to pick out maximum orders in the shortest service time before the due time. The on-line order batching mixed-integer programming model considering orders′ due time is established to minimize the valid average service time of distributed orders. To solve this problem, the improved fixed time window order batching algorithm is proposed. The order is identified as the urgent one if its remained operation time is between lead time and distribution setup time. Based on orders′ different urgent level, we propose the on-line order batching rules while taking into account urgent degree and similar degree. Through a series of experiments where the orders are generated from 14:00 to 18:00 based on Poisson distribution (λ=17), we compare the results with ones of traditional on-line order rules. Several enlightening findings are discovered: If considering orders′ due time, the number of distributed orders is bigger, the batches′ total service time and the distributed batches′ valid average service time are shorter, and the number of delayed orders is smaller and delayed time is shorter. Meanwhile, if considering orders′ due time, with the increase of the number of order pickers, the delivery rate improves in different degree, and the increase of delivery rate is larger than the one of traditional rules. However, the increasing of delivery rate is a progressive decline. e-commerce;on-line order picking;order batching;due time Date:May 5th, 2014 DateOctober 30th, 2014 FundedProject:Supported by the National Natural Science Foundation of China(71171029,71350011) Biography:Dr.Wang Xuping, a Liaoning Jinzhou native(1962-), graduated from Dalian University of Technology and is a Professor and Ph.D Supervisor in the Institute of Systems Engineering and School of Business at Dalian University of Technology. His research interests include e-commerce and logistics management, emergency management, etc. E-mail:wxp@dlut.edu.cn F713.365.1 A 10.3969/j.issn.1672-0334.2014.06.009 1672-0334(2014)06-0103-11 2014-05-05修返日期2014-10-30 国家自然科学基金(71171029,71350011) 王旭坪(1962-),男,辽宁锦州人,毕业于大连理工大学,获管理学博士学位,现为大连理工大学系统工程研究所和商学院教授、博士生导师,研究方向:电子商务与物流管理、应急管理等。E-mail:wxp@dlut.edu.cn □4.3 基于紧急程度的订单分批优化算法
5 传统在线订单分批算法
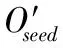
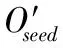
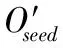
6 数据实验和结果分析
6.1 实验参数设置
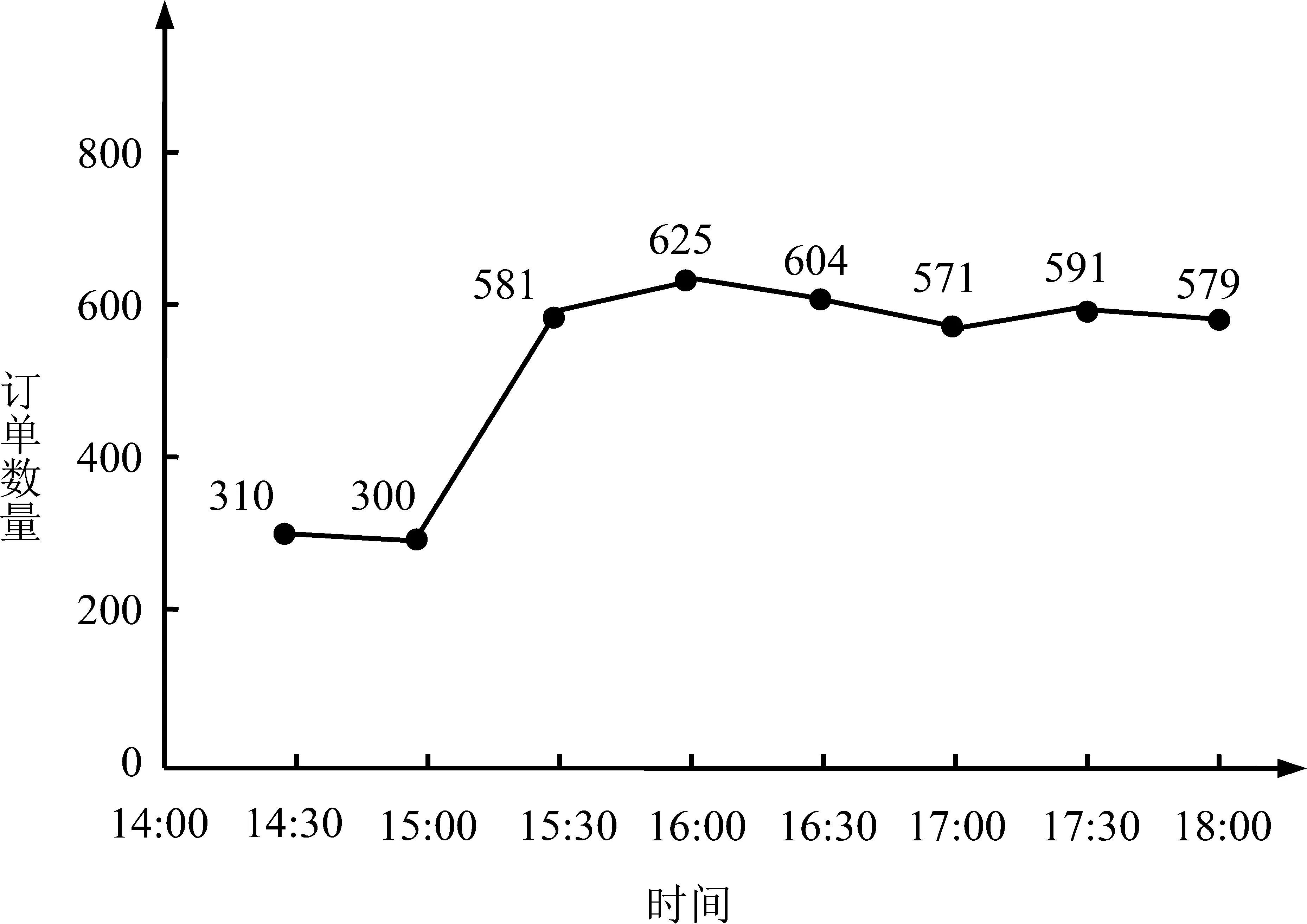
6.2 结果分析
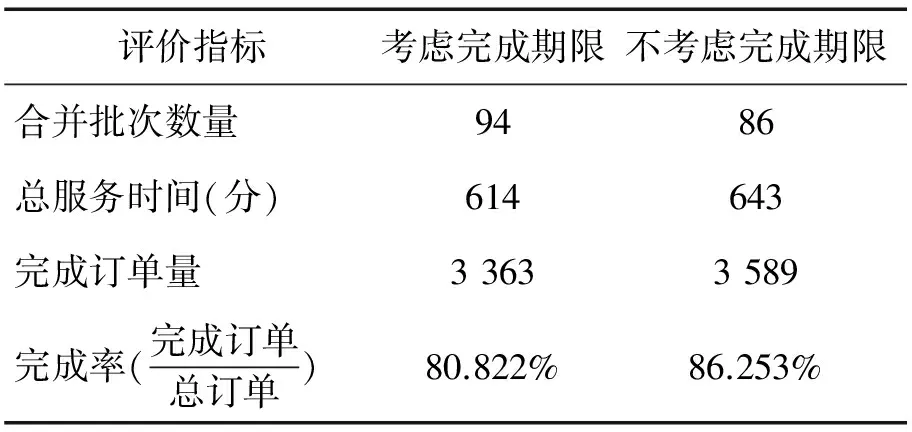
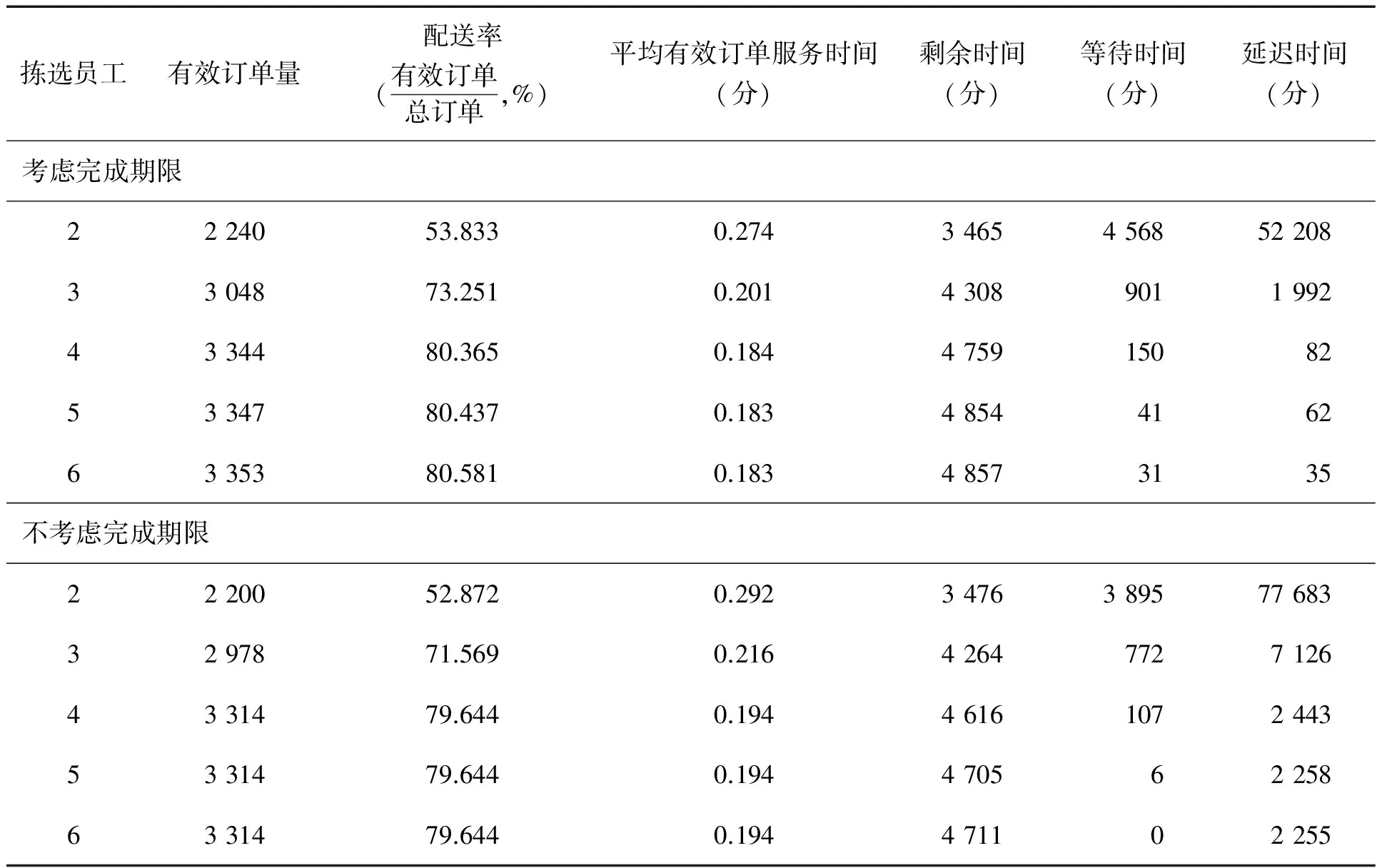
7 结论